一种改进型关联规则算法设计与研究

邓 毅，邓晓慧

（1.重庆科创职业学院 人工智能学院，重庆 永川 402160 2.重庆城市职业学院 商学院，重庆 永川 402160）

1 Apriori算法概述

AIS算法是较早被用来解决关联规则问题的算法，但此算法在使用的过程中性能较低，于是Agrawal等人在此前的应用基础上，对AIS算法进行了相关的改造，Apriori算法此时便被提出来了，且成为利用关联规则进行数据挖掘较好算法之一[1]。依据Apriori算法，延伸出了类似Apriori-Hybrid、DIC、AprioriTid、DHP等算法。

1.1 Apriori算法过程

在Apriori算法运行之前，用户需要首先设定好最小支持度，一旦开始扫描事务数据库时，就仅计算每一个项目的具体值的数量，来确定大型1--项集，后面的n次遍历，都将重复连接与剪枝的操作，直到产生的项为空，停止算法。该算法的流程图如图1所示[2]。

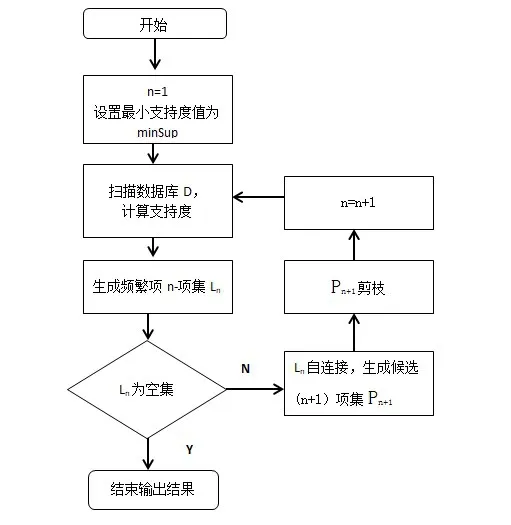
图1 算法执行过程

该算法通过逐层的迭代来得到需要的频繁项集，获取频繁项集的算法伪代码如下所示：

算法：Apriori算法生成频繁项集

输入：事务库D；最小支持度阀值minSup

输出：D中的频繁项集L

方法：

L1={发现频繁1-项集}；

For(n=2;Ln-1≠φ;n++)

{

Cn=apriori_produce(Ln-1,minSup);

for each transactionT∈D{

CT=sub set(Cn,T);

for all candidate c∈CT

C.count++;

}

Ln={c∈Cn|c.count≥min Sup}

}

Return L={UnLn}

在该算法的伪代码方法中，Ln-1和min S up这两个值作为函数apriori_produce的参数值被代入，获取了候选n-项集Cn,这个函数进行了两个操作：连接操作、剪枝操作，如下所示的实现步骤[3]：

Function apriori_gen(Ln-1,minsup)

For each itemset S1∈Ln-1

For each itemset S2∈Ln-1

c=s1⊲s2;

If exist_infrenquent_subset(c,Ln-1)

{

Delete c;

}

Else fill cnwith c;

}

Return cn

在完成了上述的n--项集后，使用Apriori的性质，需要对Cn进行剪枝的操作，删除掉拥有非频繁子集的候选。用于对非频繁子集测试的函数实现如下：

Function exist_infrenquent_subset(c,Ln-1)

for each(n-1)-subset p of c

If p∉Ln-1

Return true;

Return false;

1.2 Apriori算法实例解析

由于伪代码语言并不能够清晰的说明Apriori算法的执行过程，接下来将通过一个使用该算法产生关联规则的例子来说明。如表1所示的交易数据库Q。

表1 交易数据库Q

在算法实施的过程中，支持度用项集出现的次数来表示，设定挖掘的过程中，最小支持度的阀值为2，该算法的执行步骤如下：

首先，生产频繁项集。当对交易数据库Q完成扫描后，会得到候选1-项集C1：{M1}、{M2}、{M3}、{M4}、{M5}。因为生成的每个项集的支持度的值都大于或者等于设定的2，所以C1中的所有的项集都被包含在1-项集L1中。

对第一环节中的1-项集L1进行自连接，得到候选2-项集C2：{M1,M2}、{M1,M3}、{M1,M4}、{M1,M5}、{M2,M3}、{M2,M4}、{M2,M5}、{M3,M4}、{M3,M5}、{M4,M5}，在L1中包含了他们所有的子集，不需要剪枝操作[4]。接着完成这些候选项集的支持度计算，结果如下：{M1,M4}、{M3,M4}、{M3,M5}、{M4,M5}支持度的值小于设定的阀值2。说明这些不是频繁2-项集的内容，其余都是。

2-项集C2进行自连接操作产生3-项集C3：{M1,M2,M3}、{M1,M2,M5}、{M1,M3,M5}、{M1,M3,M4}、{M2,M3,M5}、{M2,M4,M5}。因为{M3,M5}、{M3,M4}、{M4,M5}都不在L2里面，所以可根据Apriori的性质得出后面四个选项是可以被剪枝的。只需要对候选项集{M1,M2,M3}、{M1,M2,M5}进行计数，就可以获得3-项集C3。

3-项集L3进行自连接就可以获取到4-项集C4：{M1,M2,M3,M5}，由于{M1,M3,M5}不在L3里面，所以要进行剪枝，最后得到L4为空集，到此为止，算法计算完成。

最后经过Apriori算法得到的频繁项集为：{M1}、{M2}、{M3}、{M4}、{M5}、{M1,M2}、{M1,M3}、{M1,M5}、{M2,M3}、{M2,M4}、{M2,M5}、{M1,M2,M3}、{M1,M2,M5}。

然后，将以上得到的所有的频繁项集继续处理，得到需要的强关联规则。拿{M1.M2,M3}为例进行说明，{M1,M2,M3}的全部非空子集为：{M1}、{M2}、{M3}、{M1,M2}、{M1,M3}、{M2,M3}，那么可能的关联规则计算如下：

如果将最小置信度的阀值设定为40%，那么就可以将上述计算得到的Confidence的值与设定的40%进行比较，选取其中大于该值的规则。从上面的计算结果来看，第4、5、6条规则满足条件，即得到这几条是强关联规则。

按照以上的方法对其他的频繁项项进行类似的操作，就可以得到全部的规则。

2 Apriori算法的性能分析

Apriori算法的核心思想为：候选产生-检查。这种方法的优点为：对候选K-项集采取了有效的裁剪，可以大大的降低了候选集的大小，从而减少了计算量。缺点为：当设定的最小支持度的阀值比较小，相反事务集量较大，就会表现出性能上的不足，主要体现在以下几个方面[5]。

第一扫描事务数据库次数较多；

第二可能会生成较大的候选集；

第三产生过多的无用的规则。

2.1 Apriori算法的优化

通过上文对Apriori算法的介绍和分析，该算法容易被人理解和接受，但是其也存在需要解决的问题，需要对该算法进行部分的优化。通过查阅相关的文献资料，专家及学者对该算法的优化思想，主要有以下几个方面。

2.1.1 基于哈希的方法

该方法的主要思想为：将哈希技术运用到频繁2-项集的获取上面。如果最小支持度的阀值大于某一个K-项集在哈希树路径上的计数值，那么该项不会是频繁的。

2.1.2 降低交易个数的方法

该方法的原理为：不包括任何K-项集的事务一定不包括（K+1）项集。通过使用该方法减少未来需要扫描的事务记录，从而提高算法的效率[6]。

2.1.3 基于采样的方法

该方法通过抽取数据集中的部分数据作为样本，得到可能在整个数据集中成立的规则，然后利用未作为样本的数据进行规则的验证。此种方法减少了I/O的操作，但是降低了数据的精度，可能会导致数据扭曲，针对此种现象，很多学者也讨论了反扭曲的相关算法[7]。

2.1.4 间隔计算的方法

该方法的过程为：首先由CK直接生成CK+1，得到CK+1的支持度进而获取LK+1，从而不需要计算的CK支持度来获LK，减少了数据库的一次扫描。使用该方法的前提条件是生成的候选项目集CK+1要能够被放进内存。

3 Apriori算法改进

3.1 Apriori算法改进思想

通过对Apriori算法性能及算法思想的分析，该算法还是存在一定的缺陷[8]。尽管很多的专家学者针对某些缺陷，提出了一些解决方法，但仍然有扫描事务数据库次数较多，准确度不精准的问题，主要体现在以下两个方面：

第一为了获取候选频繁集的支持度，需要多次扫描事务库，I/O的开销很大，当数据的量较大时，算法的执行效率低下，花费的时间较长[9]。

第二在频繁集连接时，没有考虑到现实的意义，让很多无关项集参与到了连接，导致了大量的候选项集产生，最后也导致了自连接和后剪枝的量的增加。

在本次的研究中，针对第2个问题进行改进，主要在原Apriori算法基础上引入事先剪枝的方法，来降低候选集的数目，从而提高数据挖掘的效率。

3.2 事先剪枝策略

Apriori原算法是LK-1在进行自连接后，可以得到候选集CK，利用算法的性质对CK进行剪枝操作。改进之后的思想为：如果在CK被生成之前就能够判断出那些非频繁，那么就可以提前剪掉这些项集。优点为：避免了为产生这些项集的连接操作，同时也省去了在扫描事务库时的支持度频度需要计算的问题，进而减少了算法计算的时间，下面结合频繁项集的几个性质来进行算法改进的说明。

第一如果K-项集X是频繁项集，那么X下的全部（K-1）项子集都是频繁项集；

第二如果K-项集X里面（K-1）项子集不是频繁项集，那么X就不会是频繁项目集；

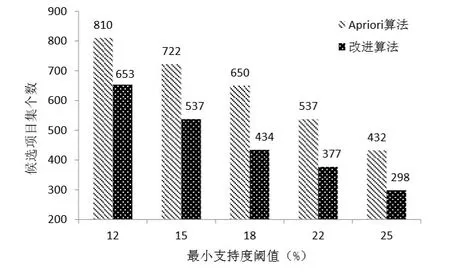
第三如果K-项集X={i1,i2,...,ik}中，满足S∈X，且LK-1(S)

对第3条性质进行证明：若X是频繁K-项集，则LK-1包含K个K-1项子集。在这些子集中，单个项目S(S∈X)总计出现了k-1次，因此对∀S∈X，都满足|LK-1(S)|≥K-1，和条件矛盾，所以X不是频繁项目集。

由第三条性质可以得到，如果LK-1里面有元素L包含了s,满足|LK-1(S)|≥K-1，那么LK-1中除去之外的L全部元素与L连接，得到的K-项集全部不是频繁项目集。由L进行连接得到的候选K-项集是非频繁的，就不需要让L加入连接。

结合上述的相关性质，具体的事先剪枝实施步 骤 如 下 ：第 一 算 出 |LK-1(S)|，其 中S∈{⋃A|A∈LK-1}，则算出LK-1中单个项目出现的次数；第二记录频度低于K-1的项目，标记为U={S||LK-1(S)

在完成第4步的L'K-1的自连接之后，使用原Apriori中的后剪枝可以进一步的减少候选集的规模。使用改进的事先剪枝策略可以实现降低频繁项集连接操作的时间花销，也实现了降低后剪枝操作时的工作量。使用该策略减少了候选项集的数量，同时变相的也减少了扫描数据库的I/O开销，降低了算法的运行的时间复杂度[10]。

4 算法改进性能评价

为了能够获取改进后算法的性能，本小结将改进前后的算法进行比较分析。实验比较的数据分为两个方面：在不同的最小支持度阀值下，产生的候选集数量和运行的时间。

实验环境：

操作系统：windows 7 Professional。

仿真环境：Matlab R2012a。

测试使用数据：选取UCI标准测试数据集Mushroom,此种数据的特征就是频繁项目集密集分布。

实验步骤：

第一使用相同的数据集，设置不同的最小支持度阀值，比较改进前后的不同支持度下的候选集数量，如图2所示。随着最小支持度的阀值的增加，候选集的数目都在减少，但是在相同的支持度下，改进后的算法生成的候选集数目要少于改进前。

图2 不同支持度下的候选项集

第二使用相同的数据集，设置不同的最小支持度阀值，比较改进前后的运行时间，如图3所示。通过实验结果表明：改进过后的算法在不同的支持度下的运行时间都要小于改进之前的运行时间。

图3 不同支持度下的运行时间

5 基于U检验思想置信度评价

在实际的关联规则挖掘中，基于传统的支持度-置信度的Apriori算法存在着一些问题。例如：不能够得到更加有效的关联规则。针对此问题，本论文在研究时，在Apriori算法基础上，采用了基于U检验思想衡量标准，即：通过限制、约束关联规则的产生方式，得到需要的强关联规则。

U检验数学算法思想：设一个拥有K属性的总体样本为S，对象的总个数为计为n,拥有K属性的对象个数为m,那么具备该条件的对象在S中的比率为：P=m/n。使用U检验，可以比较总体百分数P0与样本百分数P之间的差异。该差异值用标准差SP，计算公式如下所示。

利用以上的两个公式，可以得到如下的差异关系：

(1)|u|

(2)u0.05≤|u|

(3)|u|≥u0.01，p与p0显著性差异很大。

在事务集L中，一个X项对另外一个Y项的影响度的大小，可以利用期望置信度及置信度之间的差异来表现。结合上述的公式，得到关联规则的影响度定义公式如下：

若P(Y)=1且P(X)<1,规则的影响度值为0;

当满足最小支持度和最小置信度时，依据影响度，可以将支持度-置信度生成的规则分为三类，如表2所示。

表2 关联规则分类a

在T分布下，一个样本容量为n,ua表示为显著水平为a下的临界值u的最小影响度。如果n的值比较的大，可以得到ta(n)≈ua，ua为临界u值。如果e ffect(x⇒y)>ua，那么此时得到的关联规则为正关联规则，是值得研究的规则。一般取a=0.05作为显著性校验水准，此时得到u0.05=1.96。依据临界值的大小和影响度的大小，在本次的研究中，表明可以得到置信度较高的规则。

6 结语

本文在针对关联规则算法Apriori算法扫描次数过多、产生过多无关规则及算法效率不高的问题，采用了事先剪枝的方法进行改进，通过使用Matlab对改进的算法进行了评测，同时使用了U检验思想衡量标准的算法对评测的结果进行信度测算，实验结果表明，改进后的算法较好的解决了以上的问题，在后续的研究中，可以进一步的优化算法产生更强的关联性规则。