高填方土石混合边坡不同联合加固方式的数值模拟比较

董家豪， 宁 宇， 黄青富， 张一平， 石 崇

（1.河海大学岩土工程研究所，南京 210098； 2.中国电建集团昆明勘测设计研究院有限公司，昆明 650051）

在我国中西部地区建设发展中，由于山区丘陵等地形限制［1］，常遇到高填深挖等大型土石方工程，填方的土石混合料多为就地取材、其力学特性较为复杂［2］. 国内外学者的研究表明，在填筑高度较低时，单一的抗滑桩、挡土墙、锚索可以保证土石混合体的稳定性. 但随着填筑高度的增加，土石混合料形成的边坡容易发生失稳［3-4］，单一的支护结构也难以抵抗巨大的滑坡推力，这使得工程运行存在安全隐患［5］. 因此以抗滑桩、锚索、挡土墙为基础的，能适应复杂受力情况的联合支护结构具有很重要的研究意义.

高填方一直是工程领域的重点关注问题，具有多种联合支护方式. 尉学勇等［6］利用有限差分法得出抗滑刚架桩挡土墙的计算公式，并明确了适用条件. 潘彪［7］基于工程实例分析了锚索桩承式挡土墙特性，并提出了简化计算方法. 刘滨源［8］对3 类组合支护结构进行了分析，并提出桩-墙组合支护结构的力学模型.Wu等［9］、吴红刚等［10］通过制作室内模型，研究锚拉式挡土墙对边坡的影响.

多种联合支护结构的合理选型直接影响土石混合体的稳定性，但是由于高填方受力和边界类型复杂，高填方的联合支护的计算方法和结构选型都超出了现有的规范要求. 近些年来，许多学者［11-14］采用数值模拟方法进行边坡治理研究. 其中Hatami和Bathurst［15］、Huang等［16］对加筋挡土墙进行了FLAC3D数值模拟研究. 姜华［17］利用UDEC针对边坡破坏失稳模式提出了微型桩-锚索联合支护结构. 张星等［18］利用Abaqus研究了大型节理岩坡中联合支挡结构的支挡效果. 薛鹏鹏等［19］利用FLAC3D对比分析了抗滑桩挡土墙和抗滑桩承台挡土墙联合式支护结构，认为多种联合支护体系对边坡的抗滑更有利，对于高填方中遇到的大型土石混合物，联合支护结构会更加合理. 由于联合支护类型众多，合理的选型可以在保证稳定的前提下，降低费用.因此本文基于锚索、抗滑桩、衡重式挡土墙设计了3种联合式支护结构. 依据地质勘探资料和相似工程经验对岩层和土体进行参数赋值，并模拟土石混合物边坡的失稳过程，分析不同组合结构的受力情况选出最优结果，并探讨最优联合结构内各部分的协调受力情况.

1 常见支护型式受力分析

由于在高填方区域的受力极为复杂，因此有必要对各支护结构的受力进行简化计算.

1.1 挡土墙受力计算

上墙破裂面上的土压力计算为［20］

式中：Ea为作用在破裂面上的土压力，γ为土体重度，H为土体深度，Ka为主动土压力系数.

根据力的多边形关系，可求得土压力分力，如图1a所示.

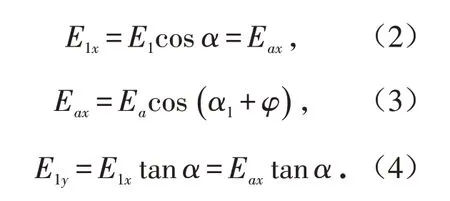
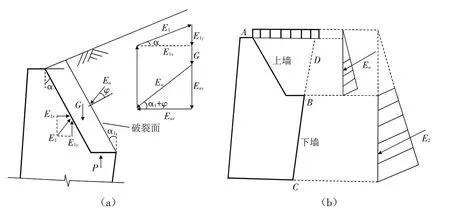
图1 衡重式挡土墙受力示意图Fig.1 Schematic diagram of the force of counterweight retaining wall

其中：α为墙背与垂直线的夹角，α1为破裂角，φ为土体的内摩擦角.

工程计算时土压力按三角形分布，作用点在上墙下三分点处.

下墙土压力计算按照延长墙背法计算，延长BC线到边坡的表面于D点，BD所处的平面假定为墙背，根据库伦土压力计算此处土压力和应力分布图，将其与BC处对应部分为下墙土压力，此部分为下墙主动土压力E2，如图1b所示.

1.2 预应力锚索受力计算

图2 为锚索治理边坡示意图，预应力锚索承担滑坡推力的计算公式［21］为

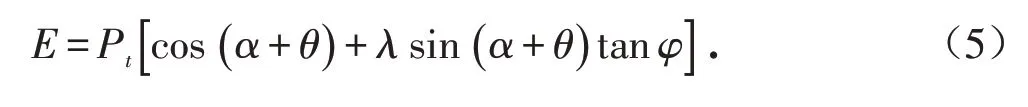
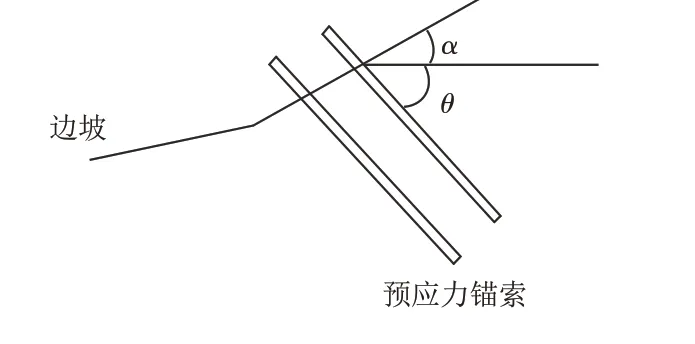
图2 锚索治理边坡示意图Fig.2 Schematic diagram of slope treatment with anchor cable

式中：Pt为锚索设计锚固力，α为边坡倾角，θ为锚索与水平方向的倾角，λ为折减系数.

根据传递系数法可得，传递到第j块处n束锚索承担的水平推力总和EjN：

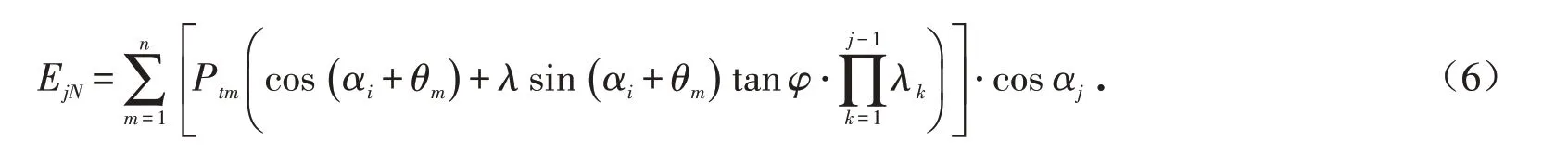
式中：Ptm为第m束锚索的设计锚固力，αi为第i块边坡倾角，θm为第m束锚索的倾角，λk为传递系数.

1.3 抗滑桩受力计算

对于抗滑桩，前后桩身承担的主动土压力按照土体比例系数法计算［22］：

其中：L为桩间距，H为桩身自由段高度，σa为朗肯主动土压力.

联合支护在简单荷载作用下，可以对各支挡结构求出相应的简化解析解. 但在高填方等复杂受力情况下，各支护类型间的内力计算极为复杂，基于有限差分法的计算软件可以应对大变形和复杂受力计算，因此本文依托有限差分软件对复杂受力下的多种联合支护可对进行稳定性分析.

2 数值模型建立

某高填方区域，土层为第四系松散堆积层和二叠系上统吴家坪组灰岩、硅质岩、黏土岩，基岩主要为灰岩，实际开挖过程发现挡土墙下部存在3个溶室. 为保证工程安全，对深沟表层进行清基、清基至基岩，坡面修设抗滑台阶，并用土石混合物对深沟进行填充，对溶室使用C10混凝土进行填充.

各岩层力学参数（见表1），各堆积体和基岩材料等看作弹塑性材料，并服从摩尔库伦准则.

表1 岩土力学参数Tab.1 Geotechnical mechanical parameters

采用数值模拟对土石混合物边坡进行加固模拟，如图3所示，底边长280 m，右端高度162 m，左侧高度50 m. 模型计算过程中模型z方向底部及x方向两端边界固定. 边坡设置了三种类型岩层，自下而上分别为基岩、强风化带、土石混合物.

图3 边坡模型Fig.3 Slope model

根据在建工程高填方的实际情况，建立以衡重式挡土墙为主的联合支护结构，支护结构包括以下4 种结构. 工况一：衡重式挡土墙；工况二：衡重式挡土墙+预应力锚索；工况三：衡重式挡土墙+抗滑桩；工况四：衡重式挡土墙+预应力锚索+抗滑桩.

土石混合物预设衡重式挡土墙，衡重式挡土墙距离左侧边界距离为53 m，墙面斜率为1∶0.15，高度为40.2 m，上墙背斜率为1∶0.55，高度为20 m，下墙背斜率为1∶0.15，高度为22 m，基底斜率为1∶10，宽度为23 m，上墙顶宽度为2 m，下墙顶宽度为7 m，挡土墙的力学参数见表2.

表2 衡重式挡土墙力学参数Tab.2 Mechanical parameters of counterweight retaining wall

预应力锚索采用FLAC中的cable单元进行模拟，初始预应力值P=1000 kN，锚索总长度为50 m，锚杆间距为4 m，自由段长度为40 m，锚固段长度为10 m，锚索横截面面积为0.07 m2，锚索倾角为20°，锚索和水泥浆参数见表3.

表3 锚索和水泥浆参数Tab.3 Parameters of anchor cable and cement slurry

抗滑桩采用FLAC3D中的pile单元进行模拟，桩长为40 m，深入原始岩层深度为10 m，桩截面采用1.5 m×1.5 m的矩形桩，抗滑桩力学参数见表4.

表4 抗滑桩力学参数Tab.4 Mechanical parameters of anti-slide piles

3 天然工况下边坡安全性分析

3.1 天然工况下边坡位移分析

土石混合物堆积体顶部在侧向滑坡推力的作用下，容易产生较大位移. 在工况一仅设置挡土墙时，边坡最大位移为300 mm，挡土墙处边坡位移为40 mm，如图4 a；工况二增设锚索后，边坡最大位移降低到260 mm，但最大位移范围和挡土墙处边坡位移未发生明显变化，如图4 b；工况三增设抗滑桩后，边坡最大位移降低到240 mm，但最大位移范围明显变小，挡土墙处边坡位移降至20 mm，如图4 c；工况四增设锚索+抗滑桩后，边坡最大位移降低到220 mm，但最大位移范围变化较小，挡土墙处边坡位移降至20 mm，如图4 d.

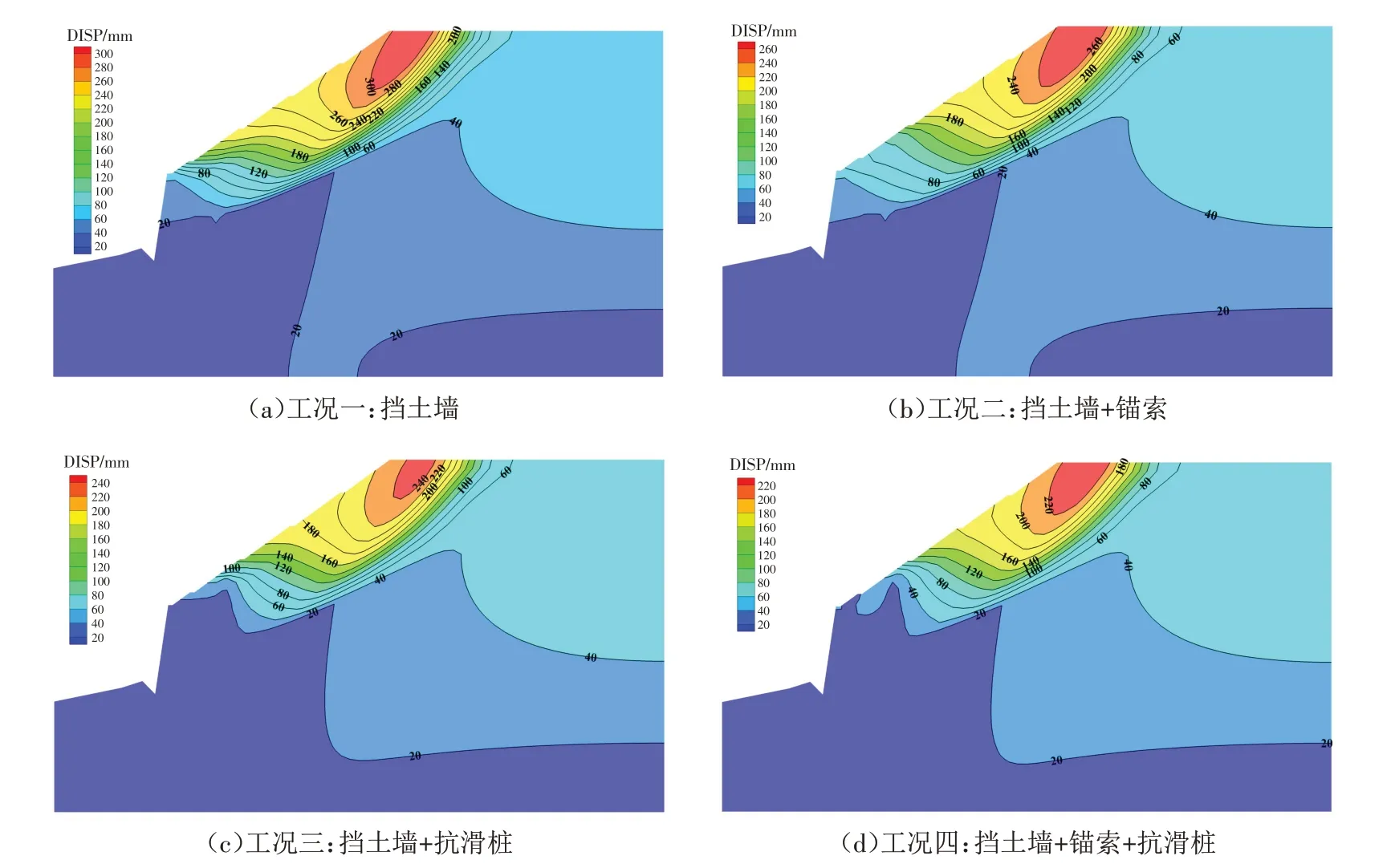
图4 不同联合支护结构的位移图Fig.4 Displacement diagrams of different combined support structures

针对不同支护结构下的土石混合体的位移，设置了6个控制点检测位移，并选取了其中2个控制点进行对比：控制点A（153，2，156），控制点B（123，2，133），如图3 所示. 并监测了各支护结构下控制点的位移曲线，随着计算步长的增加，在挡土墙基础上增设的支护结构均可降低边坡的最大位移，其中锚索+抗滑桩的组合可以最大幅度降低边坡位移，最大降幅约为30%，如图5所示.

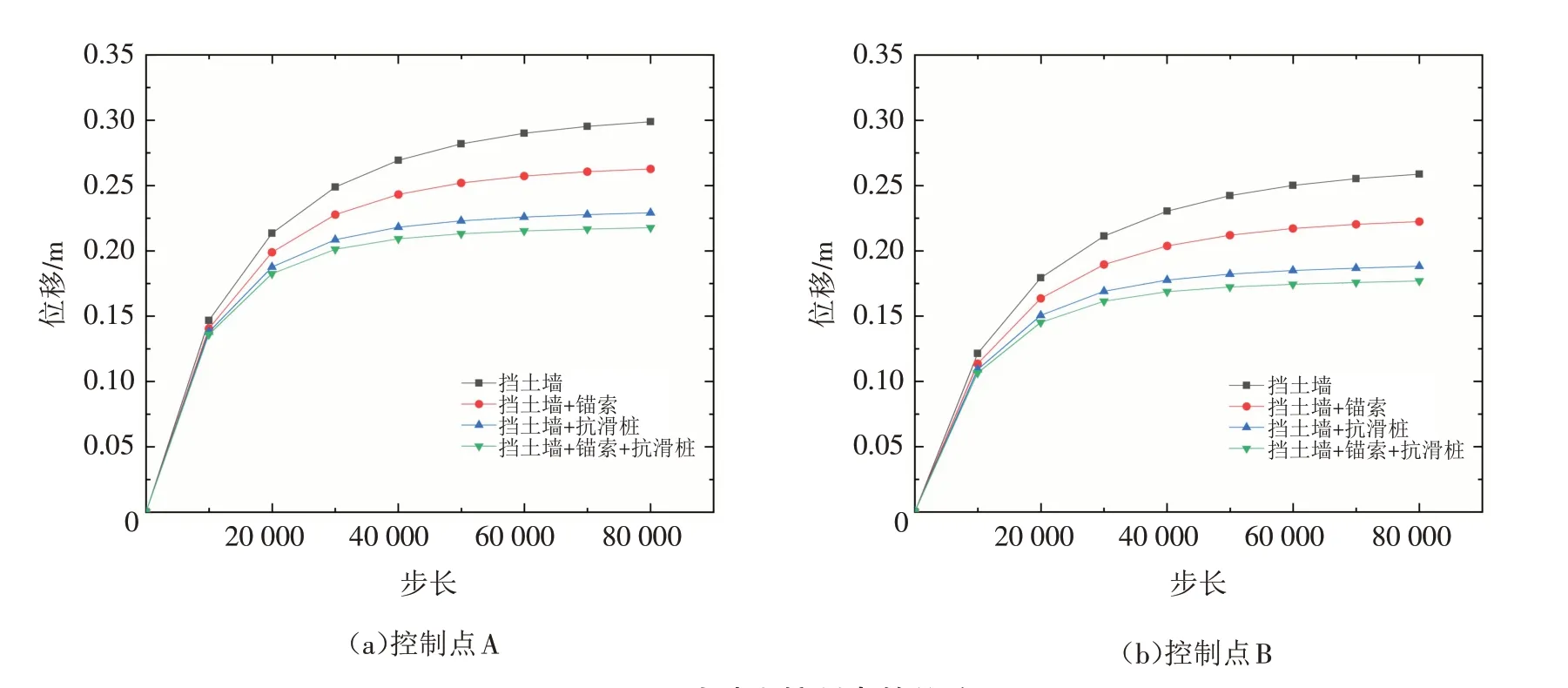
图5 边坡上控制点的位移图Fig.5 Displacement diagrams of control points on the slope

3.2 天然工况下支护结构分析

在挡土墙支护上增设的抗滑桩或锚索，都可以分别降低控制点的位移，并且锚索和抗滑桩的阻滑效果具有一定的叠加性. 为讨论阻滑效果的叠加性，对不同工况下抗滑桩的桩身位移和弯矩进行监测.图6为抗滑桩桩身位移和弯矩随桩深的变化关系，在增设锚索之后，0～25 m段桩身位移出现下降，桩顶的位移下降最大，25～40 m段桩身位移变化不明显. 锚索的增设可以显著降低抗滑桩各段弯矩，这表明边坡锚索的增设可以改善桩身受力，由于桩体稳定性的增加，使得支护结构的阻滑效果得到提升.

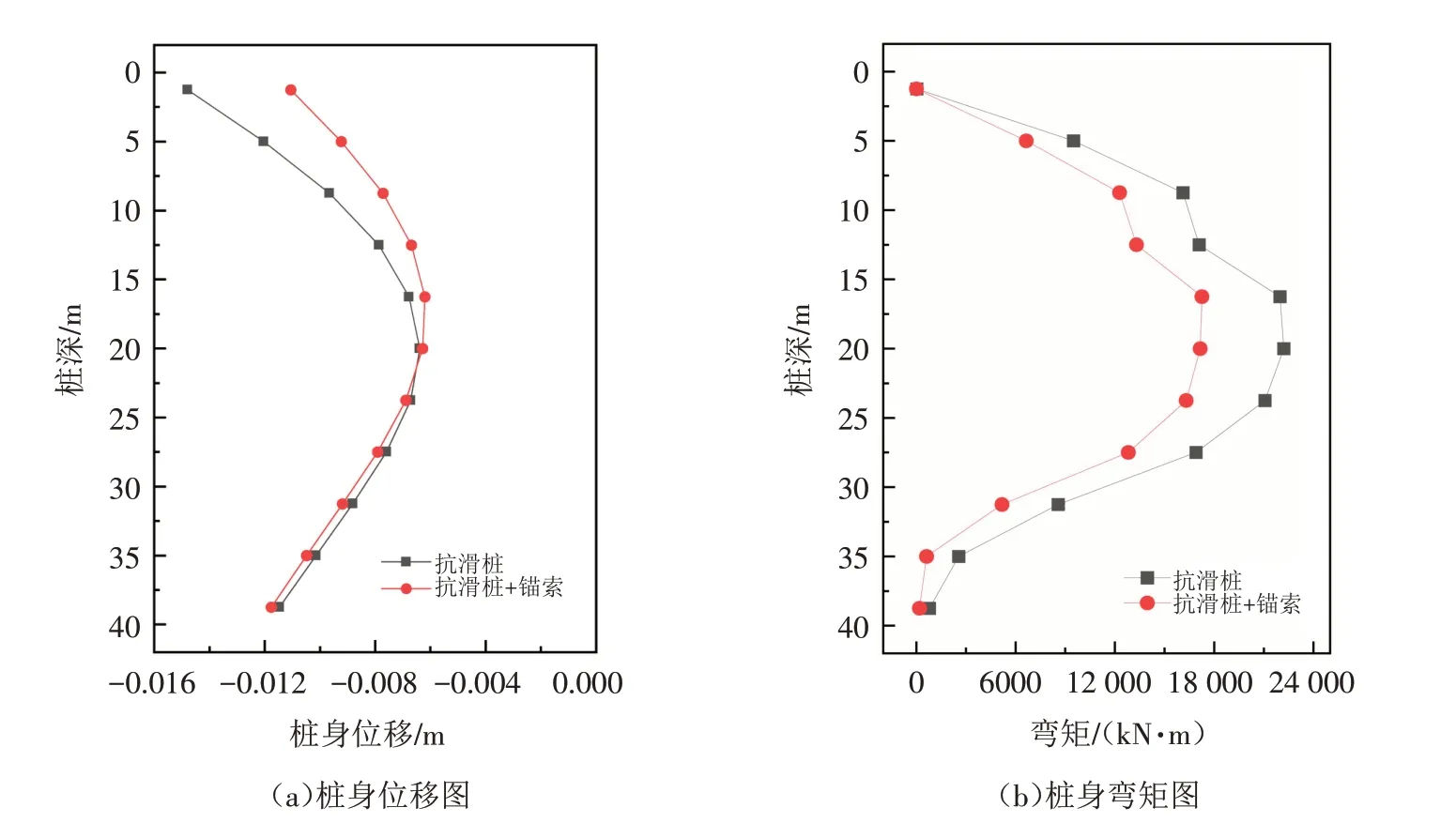
图6 不同联合支护结构的桩身位移和弯矩图Fig.6 Pile displacement and bending moment diagrams of different combined support structures

挡土墙承担土石混合物的主要荷载，挡土墙的变化直接影响土石混合物的稳定性. 因此在挡土墙上沿x方向每隔0.6 m在墙面设置监测点，对不同工况下挡土墙墙面的位移和应力进行监测，如图7所示. 随墙面宽度增加，挡土墙墙面位移逐渐增大，锚索的增设并不能降低挡土墙位移；抗滑桩的增设可大幅度降低墙面各处位移，使挡土墙墙面最大位移从0.044 m降低至0.018 m，如图7a. 墙面应力随宽度增加波动较大，最小应力出现在墙面中间，最大应力出现墙面底部，锚索的增设不能改善墙面应力；抗滑桩的增设可降低墙面应力如图7 b. 采用抗滑桩、锚索联合支护与抗滑桩支护相比，并不能更好地改善墙面位移和应力.

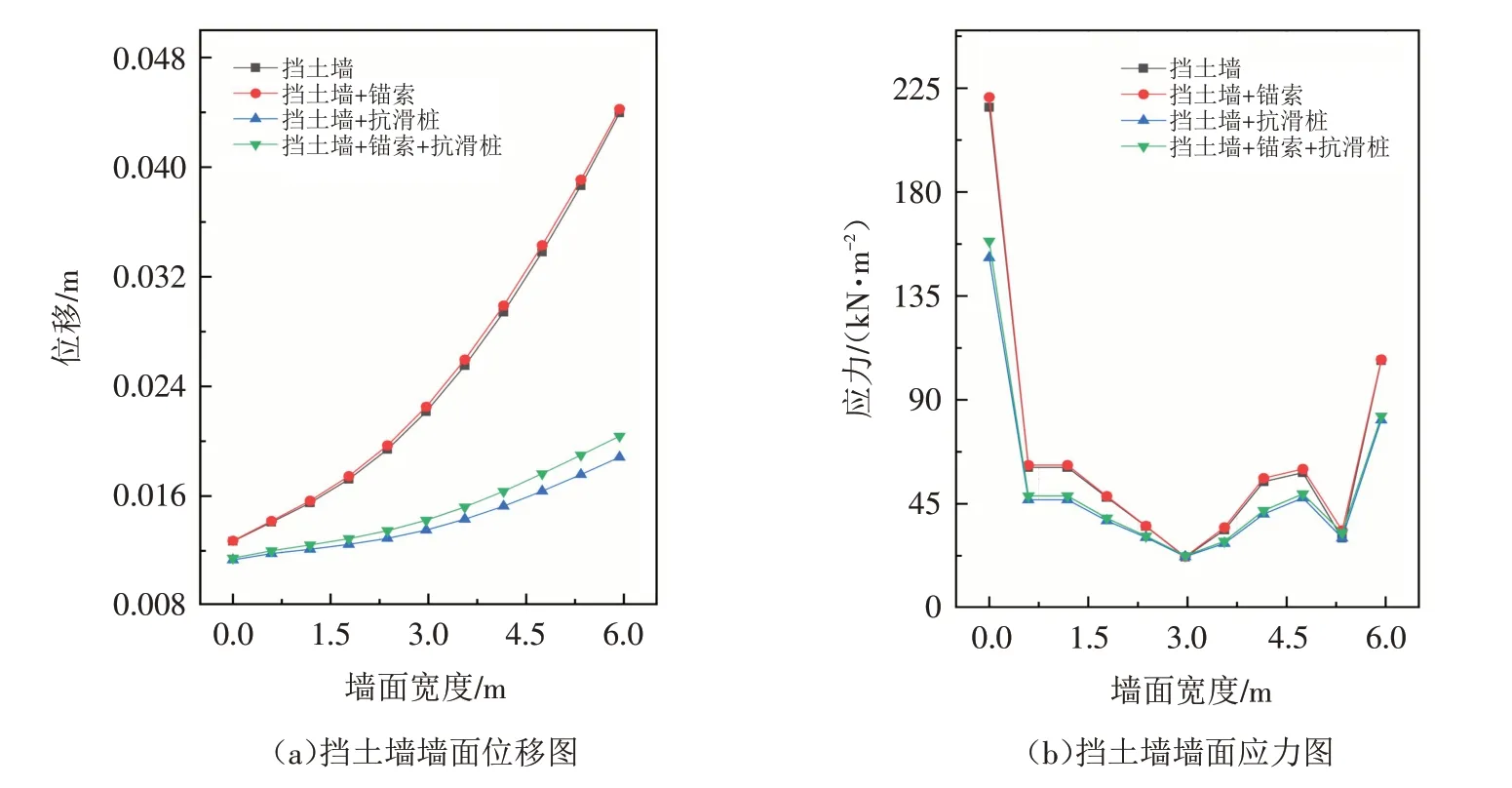
图7 不同联合支护结构的墙面位移和应力图Fig.7 Wall displacement and stress diagrams of different combined supporting structures

3.3 天然工况下边坡安全性分析

强度折减法可以分析不连续性土石混合边坡的稳定性，基本原理是利用折减系数不断折减土石混合物的强度参数，并将折减后的参数代入计算模型. 如果边坡未发生失稳，则继续增大折减系数，直至边坡失稳，此时的折减系数即为安全系数：

其中：c和ϕ分为土石混合物黏聚力和内摩擦角，ctrial和ϕtiral分别为土石混合物折减后的黏聚力和内摩擦角，ks为强度折减系数.

基于强度折减法对黏聚力c和内摩擦角ϕ进行折减后，得到土石混合物的安全系数. 工况一，安全系数为1.137；工况二，安全系数为1.191；工况三，安全系数为1.227；工况四，安全系数为1.246. 锚索或抗滑桩的加入都可以增大土石混合物所在边坡的安全系数，其中抗滑桩对安全系数的增幅效果更明显，如图8 b、图8 c. 抗滑桩和锚索联合支护对安全系数的提升具有叠加效应，这表明锚索和抗滑桩对边坡的阻滑原理是不同的，如图8 d 所示.锚索或抗滑桩的加入都可以减小潜在滑移区域，其中锚索的增设减小了最大滑移区域如图8 b，抗滑桩的增设可以显著减小整体滑移区域和最大滑移区域如图8 c.

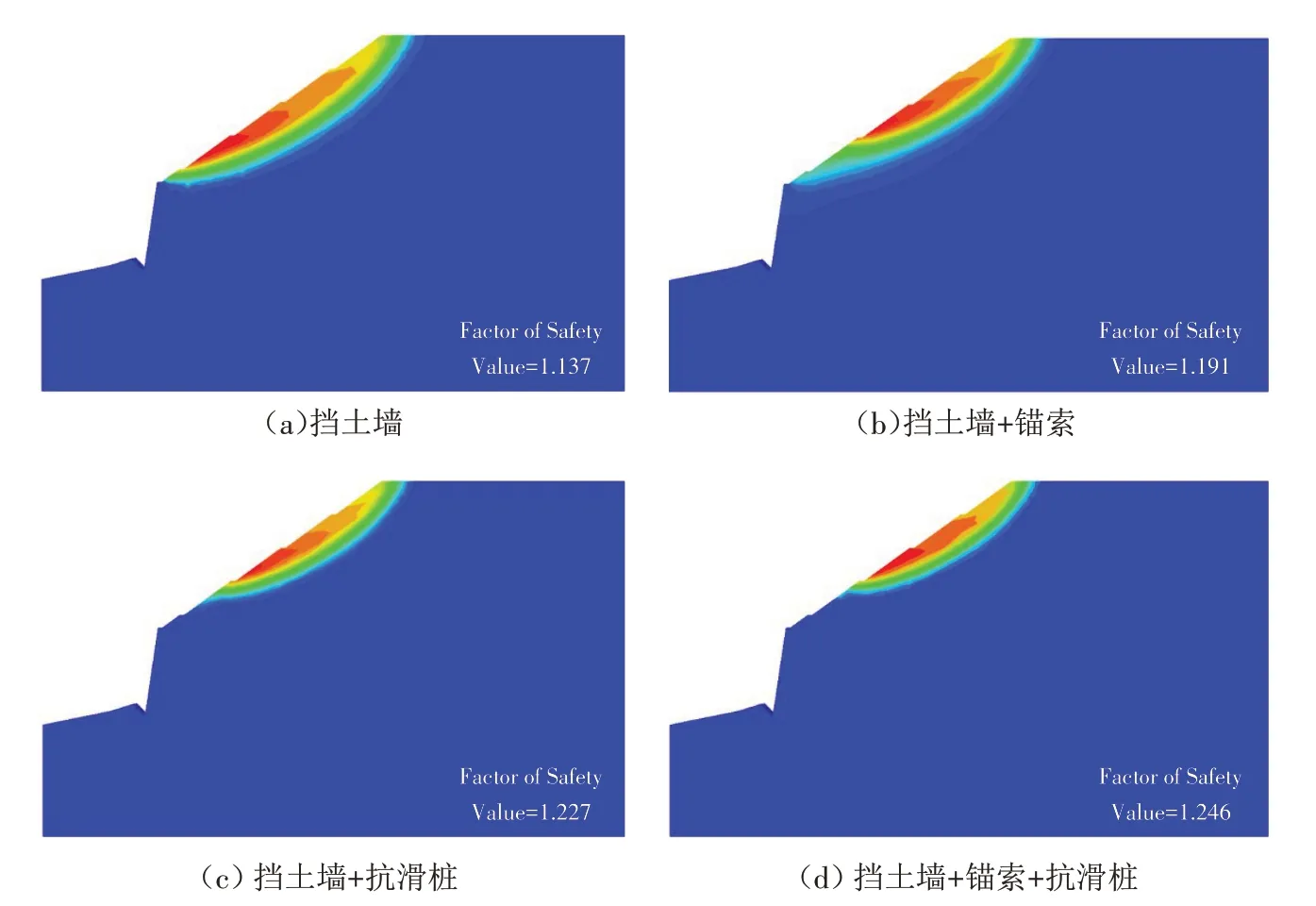
图8 不同联合支护结构的潜在滑移区和安全系数Fig.8 Potential slip zone and safety factor of different combined support structures

在仅设有挡土墙时，强度折减后的塑性区贯穿土石混合物和挡土墙，如图9 a；增设锚索后，土石混合物前段和挡土墙塑性区变大，如图9 b；增设抗滑桩后，土石混合物塑性区变小，挡土墙处塑性区消失，如图9 c；在抗滑桩基础上增设锚索后，挡土墙处出现塑性区，土石混合物前段塑性区出现扩张，中后段塑性区变小如图9 d.

图9 不同联合支护结构的塑性区Fig.9 Plastic zone of different combined support structures

4 结论

本文在采用显示有限差分方法研究不同联合支护结构在加固边坡后对土石混合物边坡稳定性的影响及提升作用，主要结论如下：

1）在挡土墙上增设的锚索或抗滑桩都可以显著改善边坡的位移和安全系数，增加边坡稳定性，其中抗滑桩的阻滑效果要优于锚索；锚索和抗滑桩与挡土墙的三种支护结构联合支护可以更好地改善边坡的位移和安全系数.

2）锚索的增设可以改善抗滑桩的位移和受力，但对挡土墙的影响极小；抗滑桩的增设可以大幅度改善挡土墙的位移和受力，增强挡土墙的安全性；同时增设锚索和抗滑桩后，挡土墙位移和受力与仅设立抗滑桩相比，并没有发生明显变化.

3）仅设立挡土墙时，强度折减后的塑性区贯穿边坡；仅增设抗滑桩时边坡塑性区面积减小，挡土墙塑性区消失；仅增设锚索时无法减小边坡和挡土墙塑性区面积；同时增设锚索和抗滑桩与仅增设抗滑桩支护相比，边坡塑性区面积没有明显缩小，挡土墙上重新出现塑性区.