基于奇异谱分析和改进萤火虫算法优化BP神经网络的时间序列预测

徐 厦， 李水艳

（河海大学理学院，南京 211100）

伴随城市化与工业化进程，有关空气质量问题愈加受到关注，对于空气质量时间序列问题的预测模型，国外，Boznar［1］对空气质量用神经网络进行预测；Kolehmainen等［2］对比多种模型，使用MLP模型来预测NO2效果最优，还有利用大量空气质量数据的天气研究与预报（WRF）模型［3］；Patricio等［4］使用线性回归模型和多层神经网络对智利某地空气质量预测；Perez等［5］通过线性算法与聚类算法，再结合多层神经网络预测PM2.5的浓度水平；Dong等［6］利用隐半马尔可夫模型（HSMMs）来预测芝加哥的空气质量水平；Dimitris 等［7］采用PCA与线性回归和人工神经网络模型结合对希腊和芬兰的城市空气质量预测；Opera等［8］利用自适应神经模糊推理系统与人工神经网络对某地的PM2.5预测；Giuseppe等［9］对BP神经网络的不足进行改进，通过所得误差代价函数优化结果. 国内，则有王娟等［10］等通过短期预测模型GM（1，1）模型对高密空气浓度进行预测；谢永华等［11］采用SVM和HSMM方法对城市PM2.5浓度分析；袁章帅等［12］利用ARMA（1，2）模型预测北京市空气质量，为改善空气质量提出建议；彭斯俊等［13］分别用灰色系统预测模型结合差分自回归移动平均（ARIMA）模型对空气浓度进行预测；Lv等［14］采用非线性回归模型对内地三个城市的PM2.5等空气质量进行预测.

空气质量数据由于受到季节变动和周期等影响，因而具有波动性. 针对这些问题，本文利用基于奇异谱分析对空气质量数据去噪，再通过非惯性权重和变步长来改进萤火虫算法，优化BP网络来建立混合预测模型.

1 理论基础

1.1 奇异谱分析

奇异谱分析（SSA）是分解原始序列包含的信号与噪声，用前几个特征值对应分量重构出新的序列来作为预测模型的输入序列.

步骤1：嵌入. 给定一维时间序列X=(x1,x2,…,xN)，选择一合适的嵌入维数即窗口长度L(2 ≤L≤N2)，且K=N-L+1，按照下列方式构造轨迹矩阵：

1.2 BP神经网络

BP神经网络结构为输入层、隐藏层以及输出层［16-18］. 因隐藏层节点的确定对网络有影响［19］，文中通过一般最佳隐含层节点的确定方法［20］，经过多次实验后，采取节点个数为15的隐藏层BP结构设计为60-15-1，结构见图1.

图1 BP神经网络结构Fig.1 BP neural network structure

1.3 标准萤火虫算法

萤火虫算法（FA）依据亮度大萤火虫吸引亮度小萤火虫来寻优，实现位置不断迭代［21-22］，过程如下.

1）初始化参数，如迭代次数和萤火虫位置等.

2）得到萤火虫的吸引度β和相对荧光度I，公式如下：

其中：β0为r=0 时吸引值；I0为最大萤光亮度；γ为光吸收系数；rij为萤火虫i与j之间的距离.

3）更新萤火虫位置，萤火虫i被萤火虫j吸引位置的更新如下，式中xi，xj为萤火虫i与j所处位置，α∈[0,1]为步长因子.

4）由更新后位置来计算萤火虫的亮度.

5）满足条件即得到全局的极值点，否则转2）步再次运行.

1.4 改进萤火虫算法

由于BP神经网络具有收敛速度缓慢［23］等不足. 本节通过将变步长和非线性权值结合得到的改进萤火虫算法（AWFA）来优化网络权重等参数［24］，再次代入BP神经网络进行预测，达到弥补BP神经网络的缺点的目标，并且兼具两者的优点，从而具有更优的准确度和收敛速度.

1.4.1 变步长 在FA算法中，对环境中一切萤火虫个体采用同一个固定的步长，存在求解精度与求解速度不高等缺陷. 因而，要采用变步长［25］的方法，即为每个萤火虫个性化地设置步长参数，能提高萤火虫优化算法的搜索能力和性能. 该算法（AFA）的改进思想为：在算法迭代期间，每进行一次就为每个萤火虫个体动态设置一个步长. 设置的考虑因素为每个萤火虫直到目前搜索到的最优位置和搜索到目前为止的全局最优位置. 具体的步长设置公式为

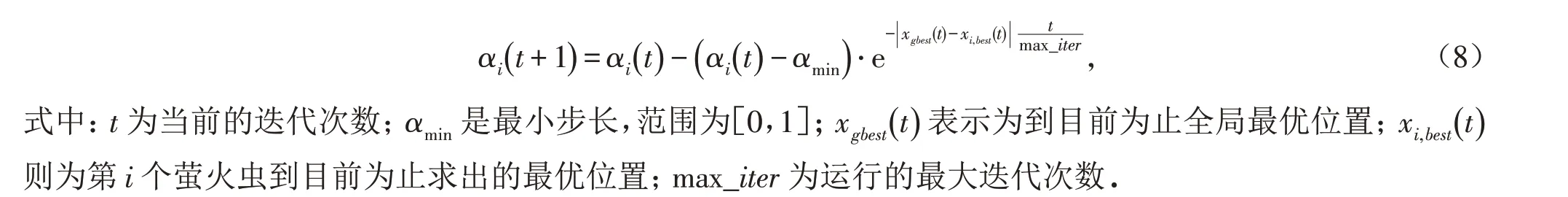
1.4.2 非线性惯性权重 为改善FA算法的收敛精度与在全局最优解附近产生震荡的不足，采用惯性权重w，位置迭代公式如下：

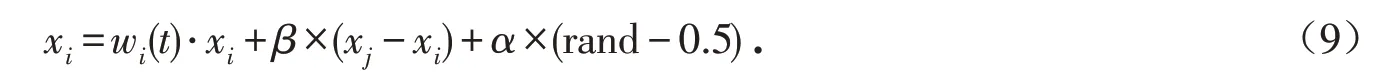
w值大会对全局搜索能力产生影响，w较小则影响公式的局部搜索能力［26］. 为了提高全局搜索能力，文献［27］采用tanh 函数作为构造非线性惯性权重的基函数，函数公式为

本文选择a=5 来进行对w构造得到的算法（WFA），w则将定义为

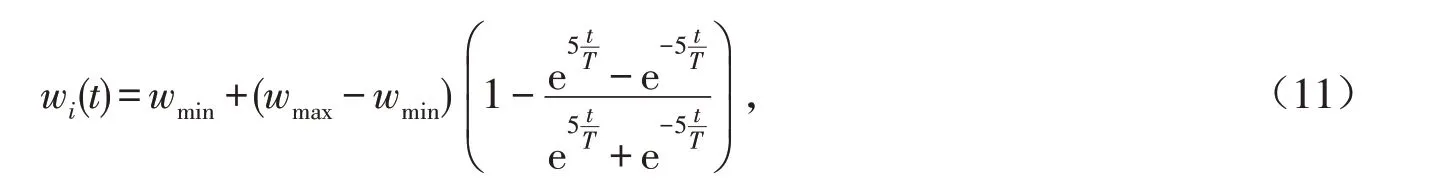
式中：t为当前迭代次数；T为最大迭代次数；wmax，wmin分别为w的最大值与最小值.

1.5 仿真实验与结果分析

1.5.1 测试函数 为了验证算法的性能，本节选取两个标准测试函数对改进算法进行实验验证，测试函数如下：

1）Sphere：单峰二次函数

2）Rastrigin：有大量局部极值点的多峰函数

1.5.2 仿真结果与分析 本节采用改进萤火虫算法AFA、WFA、AWFA 以及遗传算法GA，对两个测试函数画出寻优曲线（图2），由图结果看出，对于测试函数Rastrigin和Sphere，AWFA算法可以通过更少的迭代次数更加逼近理论最优值，因而AWFA算法的求解质量具有一定优势.

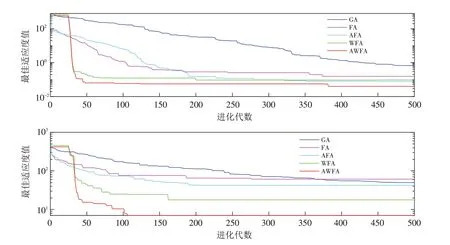
图2 多种算法在测试函数f1（上）和f2（下）结果对比Fig.2 Comparison of the results of various algorithms in the test function f1（top）and f2（bottom）

2 预测模型建立

2.1 数据

本文选取北京某地空气质量2013年10月28日至2019年12月31日的日均PM2.5浓度数据见图3.

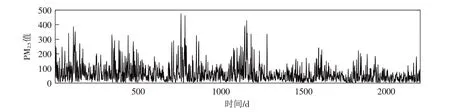
图3 原始序列Fig.3 Original sequence

2.2 奇异谱分析

在奇异谱分析中，窗口长度的选取不宜超过时间序列的三分之一，本节选取窗口长度为700来构造轨迹矩阵，根据方差贡献结果，选取前3个重构后时间序列数据见图4.

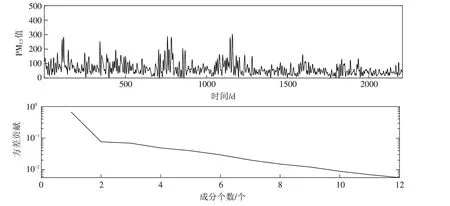
图4 重构序列（上）、方差贡献（下）Fig.4 Reconstructed sequence（top）and variance contribution（bottom）

2.3 评价指标

本节采用平均绝对误差MAE，均方根误差RMSE和平均绝对百分比误差MAPE作为评价指标如下.

平均绝对误差：

均方根误差：

平均绝对百分比误差：

式中：n为预测样本数；Yˉ(t)为预测值；Y(t)为实际值.

2.4 预测效果评估

对去噪后数据用多种预测模型，几种算法横向比较见表1，其中SSA-AWFA-BP 在处理此数据的预测指标效果更佳，性能更为优越，从而验证了模型的合理性与有效性.

表1 基于时间序列数据的预测模型选择Tab.1 Selection of prediction models based on time series data

3 结语

3.1 本文总结

奇异谱分析能够有效改善时间序列数据中噪声对模型的影响，并且提取数据中趋势项和周期成分，与单一的BP神经网络相比，去噪后预测精度更优. 再利用改进FA算法来优化网络结构，效果优于文中使用的其他模型，该模型是有一定意义的且是可行的，具有一定的使用推广价值.

3.2 展望

1）本文建立的混合模型对最大预测长度以及改进的萤火虫优化算法中的步长和权重等参数、确定SSA方法的窗口嵌入以及重构阶次等确定最优参数方面还需进一步分析以提高去噪效果. 文中只选取了奇异谱分析去噪，可以比较其他去噪算法，从而进一步改善预测效果. 可以结合概率选择［28］和精英反向学习［29］等其他改进萤火虫的优化算法.

2）为了改善预测精度，可考虑温度与风速等多种影响因素的时间序列数据，往后还要进一步研究多通道的SSA来应用于时间序列.