随机低秩逼近算法在张量近似中的应用

陈 熙 冯月华

（1.上海工程技术大学 机械与汽车工程学院，上海 201620；2.上海工程技术大学 数理与统计学院，上海 201620）

张量是一个多维数组。一阶张量是向量，二阶张量是矩阵，三阶或更高阶的张量称为高阶张量。高阶张量的分解在信号处理、数值线性代数、计算机视觉等领域都有大量的应用[1-3]。张量分解可以被认为是矩阵奇异值分解的高阶扩展。常用的两类分解分别是CANDECOMP/PARAFAC（CP）分 解[4]和Tucker 分解[5]，前者将张量分解为一阶张量的总和，而后者是矩阵奇异值分解（SVD）的高阶形式，本文主要研究的是Tucker 分解。

在计算 Tucker 分解的各种算法中，一个关键步骤是计算张量的每种可能模式展开的精确或近似的奇异值分解，这将在后面定义。为了有效地计算给定张量的可靠Tucker分解，本文基于随机算法策略以及高效数据访问的要求，提出一种新的高效算法求解Tucker 分解，并用Matlab 软件实现该算法。

1 随机算法

任意给定一个向量x∈Rn，Diag(x)表示对角元为向量x的对角矩阵。对于任意的矩阵A∈Rm×n(m≥n)，其SVD为：

其中U=(u1,u2,…um)∈Rm×m和V=(v1,v2,…vn)∈Rn×n是正交矩阵，∑=Diag(…)且1≥≥…m≥0。对于1≤k≤n，令A的秩k 截断S VD为：

在大数据分析和机器学习中，SVD 已成为一种关键的分 析工具[6]。但是这些经典算法需要高内存消耗且计算复杂度高，已经无法满足时代发展的需求。近年来随机算法的出现为构造近似SVD 算法提供了强有力的支撑。与古典数值算法比较，随机算法具有简单易实现，更高运行效率，更具鲁棒性，更少内存空间等优点。Tro pp 等人[7]基于随机投影策略提出了单步随机奇异值分解（SPRSVD）得到给定矩阵的近似SVD，具体内容见算法1。由于原始数据集只在算法最开始的时候用到，因此算法具有高效率。

2 张量近似问题

在这里回顾一些张量的基本符号和概念，这些符号将应用于后面的数值实验。关于张量性质和应用的更详细讨论见文献[8]。张量是一个d 维数组，通常用符号X∈RI1×…×Id来表示，其元素为xj1,…,jd,1≤j1≤I1,…,1≤j d≤Id。

张量X 按第n 维展开用矩阵X∈RIn×(∏j≠nIj)表示。由于这个张量有d 维，所以一共有d 种(n展)开的可能性。张量X∈RI1×…×Id的第n 维展示与矩阵U∈Rk×In的乘积得到一个张量Y∈RI1×…×In-1×k×In+1×…×Id，即：

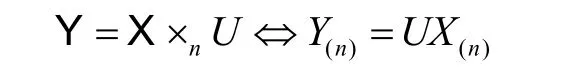
通过张量乘法和张量展开的定义，基于Tucker 分解的高阶SVD（HOSVD）。算法[9]生成一个秩为（k1,...,kd）的近似张量。HOSVD算法得到核心张量G∈Rk1×…×kd和一组酉矩阵Uj∈RIj×kj(j=1,...,d)，即：

方程（1）称为Tucker 分解。HOSVD 的计算成本和内存消耗对于大规模问题令人望而却步，因此顺序截断的HOSVD（ST-HOSVD）算法被用来提高HOSVD 的 效率[10]，该算法保留了截断HOSVD 算法的几个有利特性，同时降低了计算分解的计算成本。STHOSVD 算法的伪代码包含在算法2 中。

3 新算法STHOSVD-SPRSVD

随着实际问题中张量问题的越来越大，对分解算法的效率要求也越来越高。算法2 中计算代价最大的是每个张量展开需要计算SVD，因此算法2 中的SVD 分解将采用单步随机奇异值分解实现，进而得到更高效的Tucker 分解，并将此算法命名为STHOSVD-SPRSVD，具体细节见算法3。

4 数值实验

本节通过几个数值实验验证新算法STHOSVD-SPRSVD，并与propack 包中LANSVD 方法以及Matlab 自带的svds 命令进行比较。对应的算法分别命名为STHOSVD-LANSVD、STHOSVD-SVDS 和STHOSVD-SPRSVD。本实验通过下列方式构造一个稀疏的张量 X ∈Rn×n×n：

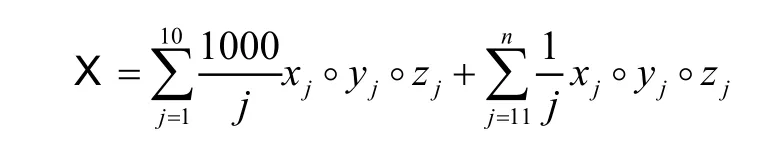
其中：x j,y j,zj∈Rn是具有非负元素的稀疏向量，符号“◦”表示向量外积。并通过使用STHOSVD-LANSVD、STHOSVD-SVDS 和STHOSVD-SPRSVD 这三种算法分别得到一个具有秩（k,k,k）的Tucker 分解[G;U1,U2,U3]。相对近似误差使用，其中,│││.│F表示矩阵的Frobenius 范数。

实验结果显示了STHOSVD-LANSVD、STHOSVD-SVDS和STHOSVD-SPRSVD 算法运行在$300 imes 300 imes 300$稀疏张量上的相对近似误差和运行时间，从结果中观察到，这三种算法的误差是可比的，但是在时间效率上STHOSVD-SPRSVD 算法比另外两种算法具有明显的优势。

5 结论

本文基于随机算法提出了STHOSVD-SPRSVD 算法得到Tucker 分解，数值实验表明STHOSVD-SPRSVD 算法在达到所要求的精度上具有更少的计算代价。由于单步的近似SVD 存在效率与精度的权衡，本文将基于现有的基础，在接下来的工作中研究具有更高精度和更高效率的算法。