还是？——“分数再认识”的一项教材微改进研究

□ 罗永军

用图来表征数学对象是小学数学概念教学的常用方法。在一次“分数再认识”的研讨活动中，为让学生进一步理解分数概念，教师请学生分别把1个圆、2个圆、4个圆看成单位“1”，画图分别表示它们的。教学很顺利，学生很快画出了示意图。其中，把2个圆看成单位“1”，学生画的是,得到了上课教师的肯定。在课后的研讨中，这幅图示引起了大家的争议，有人认为正确，有人提出质疑，认为这样画表示的是或，还有的提出在这节课中这幅图可以用来表示，到学习假分数时则应该表示为。是这样吗？同一幅图在不同时段居然可以用来表示两个不同的分数，这的确会让人产生困惑。数学不是追求精确吗？这到底该如何表示呢？

一、数学分析

分数作为一个复杂的概念，其意义非常丰富，国内外许多学者都对分数的意义进行了深入细致的研究。比如（张奠宙，2010）：

定义1（部分与整体）：分数是一个单位平均分之后的一份或几份。

定义2（商）：分数是两个整数相除的商。

定义3（比）：分数是q与p之比。

定义4（公理化）：有序的整数对（p，q），其中p≠0。

也有学者提出了更多的定义，不过在小学数学中，学习的内容涉及上述的定义1、定义2和定义3，这一次教研中的争议问题，即是与定义1有关的内容。

既然分数的定义是清晰的，那为什么会有争议呢？事实上当把1张圆片看成单位“1”，在圆片上可以表示为，这没有争议，那么在两张圆片中如何表示呢？按照定义1，我们把两张圆片看成一个单位，先把它平均分成4份：，再表示这样的3份：，涂色即表示，看来上述的图示似乎没有问题。那么，为什么大家会有争议，认为是或呢？仅从图示看，由于没有表明谁是单位“1”，还可以认为是一个圆即是单位“1”，涂色部分确实会看成3个。原来，问题出在单位“1”上，同一图示，因单位“1”不同，所表征的分数就不同。那么如何表征“单位‘1’”呢？有没有通行的方法？教材中又是如何表示的呢？

二、教材分析

像上面这样有争议的分数表征问题，教材中也有（北师大版五年级上册“分数的意义”第3课时“真分数和假分数”，如图1）。

图1

图2

图3

图4

如何让学生明确单位“1”所指呢？虽然教材中没有这方面的说明，但许多一线教师已经主动做了多种实践，最常用的方法是用“集合圈”围住多个物体，以表明围住的物体是一个整体。那么，这样图示的效果是否显著呢？

三、认知调查

我们把教材中的例题作为调查问题分别对四年级105位学生和五年级99位学生做了问卷调查，共2份，先做A问卷，再做B问卷，问卷中的图示与教材中的图示相同。其中，四年级学生未学过假分数，五年级学生已经学过假分数。之所以选择这两个年级是为了便于对比，观察“集合圈”图示法对这两类学生是否都有影响。调查时，学生均独立作答，教师不作任何解释。

A问卷 请你写出涂色部分所表示的数。

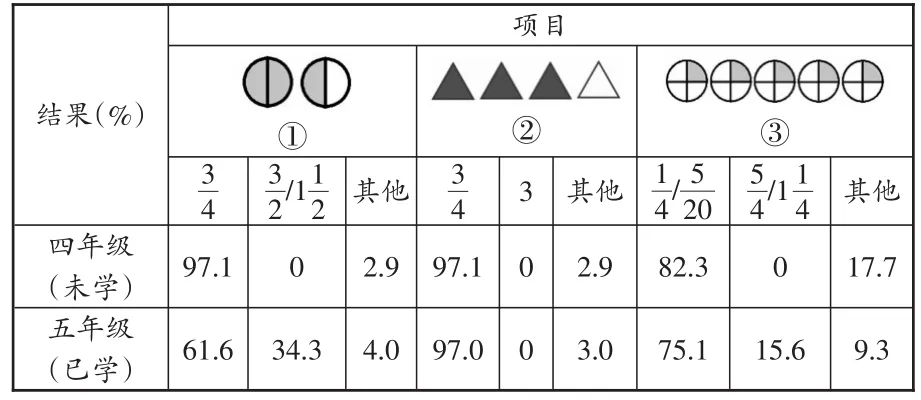
结果（%）四年级（未学）五年级（已学）项目images/BZ_58_1504_1819_1625_1877.png①3 4 97.1 61.6 3 2/11 2 0 34.3其他2.9 4.0images/BZ_58_1701_1826_1896_1871.png②3 4 97.1 97.0 3 0 0其他2.9 3.0images/BZ_58_1934_1823_2160_1874.png③15 4/20 82.3 75.1 5 4/11 4 0 15.6其他17.7 9.3

需要说明的是，虽然我们要求学生写出涂色部分所表示的“数”，但是学生受分数图式的影响，不约而同地都写成了“分数”。特别是图②，学生没有把3个涂色三角形看成3个1，而是同形继承到分数的“部分—整体”图式，全都看成了。

从调查问卷中可以明显地看到，四年级学生在未学假分数前，都默认把整体当成单位“1”，写的都是真分数，而五年级同学则按自己的理解来判断谁是单位“1”，从图①和图③的作答中可以看出写成真分数和写成假分数/带分数的学生分别接近2∶1和5∶1。这难道真是学得多，混淆也多吗？不过，这不是学生的问题，而是教材需要改进。那么，如果用上“集合圈”呢？学生会写成什么呢？

B问卷（增加“集合圈”）：请你写出涂色部分所表示的数。

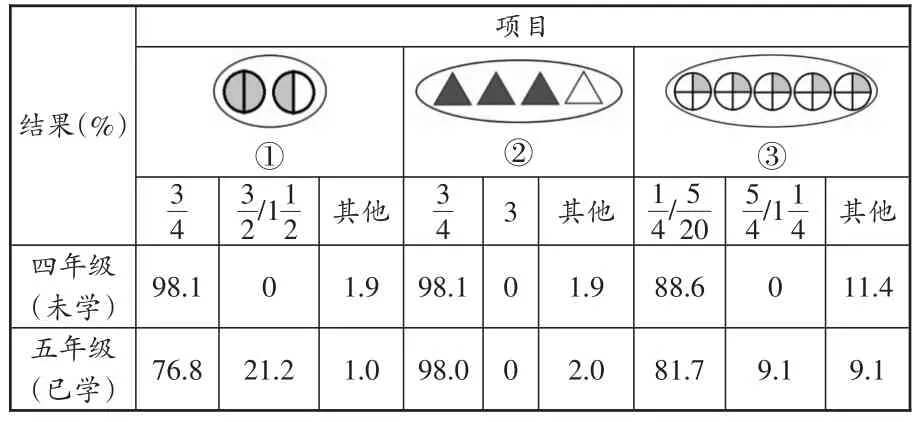
结果（%）四年级（未学）五年级（已学）项目images/BZ_59_495_554_614_630.png①3 4 98.1 76.8 3 2/11 2 0 21.2其他1.9 1.0images/BZ_59_696_557_911_627.png②3 4 98.1 98.0 3 0 0其他1.9 2.0images/BZ_59_948_554_1166_630.png③15 4/20 88.6 81.7 5 4/11 4 0 9.1其他11.4 9.1

相比较A问卷的调查结果，加上“集合圈”后，对四年级学生来说没有影响，但对五年级学生来说，正确率确实有所提升。其中，图①的正确率上升了15.2%，图③的正确率上升了6.6%，看来，“集合圈”的使用对于学生把整体看成单位“1”的理解有一定的促进作用。不过，数据也显示对于图①还有21.2%的学生认为是，看来用“集合圈”来表示单位“1”还不够直观，学生还是比较容易混淆，这确实是个有点“顽固”的学困点。

四、调整与再调查

那么，教材该如何改进呢？我们查阅了国外的一些教材，发现主要用文字说明的方法，如图5。

图5

我们认为用文字说明的方法对于学生解题作答来说会比较清晰，但还是没有解决分数的图式表征问题，或者说没有解决单位“1”的表征问题。怎么办？当我们再次审视上述的调查数据，发现使用集合圈的方法其实已经起到了一定的效果，我们设想能不能在此基础上再做进一步的改进？于是我们在原有的集合圈上增加单位“1”的标注，以进一步明确单位“1”的指向。

隔了一周，我们对原来的五年级学生再次进行问卷调查：“请你写出涂色部分所表示的数。”为提高效度，本次调查分A、B两份问卷，先统一完成A问卷，再统一完成B问卷，交叉验证。

A问卷

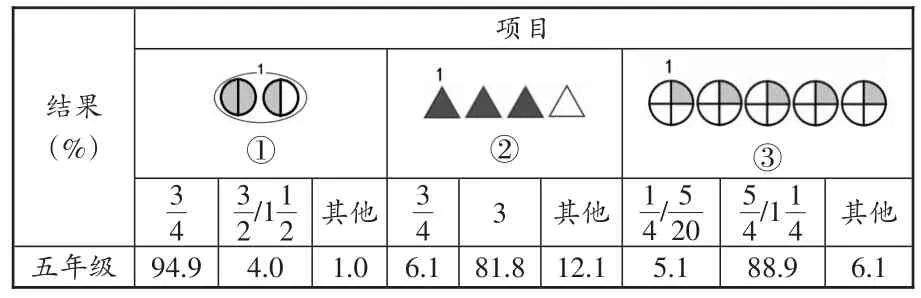
结果（%）五年级项目images/BZ_59_1485_700_1581_761.png①3 4 94.9 3 2/11 2 4.0其他1.0images/BZ_59_1692_701_1861_760.png②3 4 6.1 3 81.8其他12.1images/BZ_59_1917_693_2163_769.png③1 4/5 2 0 5.1 5 4/11 4 88.9其他6.1

B问卷

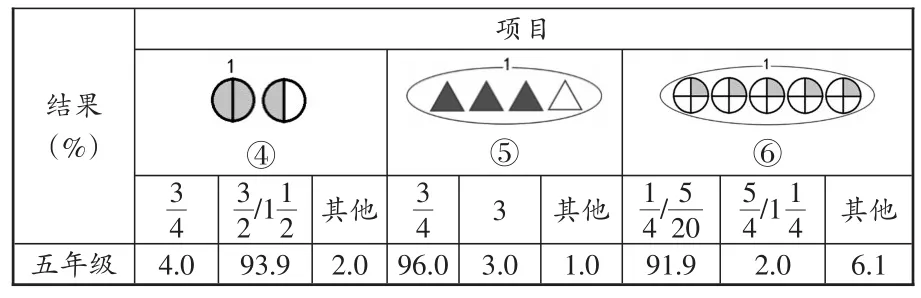
结果（%）五年级项目images/BZ_59_1481_1068_1585_1141.png④3 4 4.0 3 2/11 2 93.9其他2.0images/BZ_59_1678_1071_1876_1138.png⑤3 4 96.0 3 3.0其他1.0images/BZ_59_1931_1070_2148_1139.png⑥15 4/20 91.9 5 4/11 4 2.0其他6.1

从调查结果来看，虽然调查分两次进行而且内容互有干扰，但是学生的正确率却明显提升。其中，图①⑤⑥是把多个物体看成一个整体，学生的识别正确率达到了94.9%，96.0%，91.9%，正确率提升非常明显；在调查中，我们还对假分数/整数的表示做了调查，如图②③④，正确率分别是81.8%，88.9%，93.9%，其中最简单的图②学生反而错误最多，通过访谈了解到学生倒不是识别不出单位“1”，而是觉得写“3”太简单了不像是五年级的数学内容。回到本文开篇提出的困惑（图①和图④所示），用了新方法后，学生的正确率分别是94.9%和93.9%。看来，学生能有效地识别单位“1”所指区分，进而理解真假分数不同的表征方式。

在分数的意义教学中，学生掌握图式表征不仅有利于对意义的理解，还有利于几何直观素养的发展。本文提出了一个关于分数图式表征的教材微改进建议，是否可行，还有待于更多的一线教师、教研员、教材编者等课程建设者在更大的范围来调查验证。