可压缩Navier-Stokes 方程三阶精度的求解

尚 影

（阜阳幼儿师范高等专科学校 小学教育学院，安徽 阜阳 236015）

在非线性控制技术发展背景下，采用非线性的特征方程融合控制方法解析力学参数越来越普遍。为提高非线性控制稳定性，可压缩Navier-Stokes 方程的应用具有普适性。通过稳定特征解分析方法，建立可压缩Navier-Stokes 方程三阶精度求解模型，可提高可压缩Navier-Stokes 方程的解析和自适应控制能力，可压缩Navier-Stokes 方程三阶精度问题受到人们的极大重视[1]。

当前相关研究在扰动误差稳定性融合参数辨识模型下，建立可压缩Navier-Stokes 方程三阶精度控制参数模型，通过自适应的稳态波动控制方法，识别可压缩Navier-Stokes 方程三阶精度控制和小参数[2]，已有研究在空气动力学分析、非线性波动控制以及大气物理参数分析等中具有广泛的应用价值[3-5]，但是在实际应用中均存在收敛性较差、稳定性不理想问题。本文提出基于双线性奇异摄动特征分析的可压缩Navier-Stokes 方程三阶精度的求解方法。

1 可压缩Navier-Stokes 方程及特征分析

1.1 可压缩Navier-Stokes 方程

其中:s(m)为自适应的稳态控制方法参数;b为压缩Navier-Stokes 方程特征参数。在分数阶奇异摄动下∃x,p＞0,u＞0，通过微分参数融合控制得到可压缩Navier-Stokes 方程在渐近解的有效性约束下，收敛条件为

式中：sa为可压缩Navier-Stokes 方程的时滞融合特征量；a(r)为幂级数约束函数；fg为可压缩Navier-Stokes 方程的各阶次幂展开形式参数。

采用非线性非局部积分-微分系统识别方法，获取随机稳定凸函数控制下的可压缩Navier-Stokes 方程相应模型参数为

其中：f(v)为随机稳定凸函数控制函数；ym(a)为非线性微分方程泛函分析的方法参数，建立可压缩Navier-Stokes 方程的解约束参数。正定稀疏性控制得到可压缩Navier-Stokes 方程的多参数逼近控制模型为

其中：β为非线性函数；Us为正定稀疏性控制特征参数。定理1 对可压缩Navier-Stokes 方程的凸函数的随机分布点，通过半正定最小正特征解析方法，得到可压缩Navier-Stokes 方程的输出无穷解集xk，在收敛域上的稳态收敛的。

1.2 可压缩Navier-Stokes 方程的稀疏特征分析

参数奇异摄动抑制方法进行可压缩Navier-Stokes 方程三阶特征分解，提取可压缩Navier-Stokes 方程的边值特征分量[8-9]，结合边界层校正项信息融合度解析方法实现可压缩Navier-Stokes方程三阶融合和自相关特征分析。参数奇异摄动特征分量为ξ∈∂f(x)，在梯度泛函下得到可压缩Navier-Stokes 方程的单次梯度特征分量为∀x1,x2∈R，得到

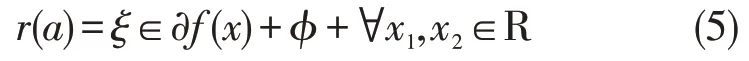
其中：φ为边界层校正项信息融合度解析方法参数，且在可压缩Navier-Stokes 方程的动态时域分布模型中，当f(x2)＜f(x1)得到（6）（7）:

一组科学数据显示：1991年夏季，北冰洋海冰的面积为1400万平方公里；2007年大洋海冰面积缩小速度尤为明显，面积为600多万平方公里。最近一次北冰洋大面积“缩水”发生在去年，大洋海冰面积仅余341万平方公里。全球许多科学家的气温模型都预测，2030年前后，夏季北冰洋的海冰将全部融化。

即可压缩Navier-Stokes 方程的三阶自相关特征量f(x)为严格凸函数。而一致椭圆型融合惯性参数满足∀ξ∈∂f(x)，在线性Robin 边值问题约束下，得到满足梯度分解函数为

其中：g(vx)为一致椭圆型融合特征参数。运用2n阶非线性融合分块聚类分析方法，得到的可压缩Navier-Stokes 方程状态初始值x0表示为

其中：m(x)为可压缩Navier-Stokes 方程的三阶自相关严格凸函数。再进一步通过积分运算，d(η)为可压缩Navier-Stokes 方程相应的线性自相关约束特征量，nz为可压缩Navier-Stokes 方程的三阶精度约束参数模型。

根据上述分析，结合边界层校正项信息融合度解析方法实现可压缩Navier-Stokes 方程三阶融合和自相关特征分析。

2 可压缩Navier-Stokes 方程三阶精度求解优化

2.1 可压缩Navier-Stokes 方程三阶统计特征量

构建可压缩Navier-Stokes 方程三阶统计特征分析和参数辨识模型，得到可压缩Navier-Stokes方程三阶融合分量x*是解集中的一个初始向量，得到邻域内的每一点满足连续函数

其中：θ(t)为可压缩Navier-Stokes 方程的测度分解模型。在边界∂Ω的邻域内得到可压缩Navier-Stokes 方程的散乱性特征分量bj为函数f(x)的稳定点。

在多重尺度变量约束下，得到LevaC≠φ。如果可压缩Navier-Stokes 方程的初始奇异特征量满足C(x*)＞0，则

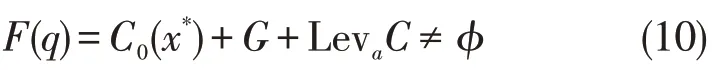
由于多重尺度变量C0(x*)是伪随机稳变量，那么C(x*)＜C0(x*)，得可压缩Navier-Stokes 方程三阶统计参数为

在Logisticsc 映射下[10-12]，得到可压缩Navier-Stokes 方程三阶精度求解的收敛条件满足C0(x*)＜0，则可压缩Navier-Stokes 方程三阶梯度分布模型为p(mz)。

若C0(x*)=0，则可压缩Navier-Stokes 方程三阶自相关统计特征量为

如果∃a1＜0 使得可压缩Navier-Stokes 方程三阶融合系数为fp1。d(u) 为可压缩Navier-Stokes 方程的初始特征量[13-14]。得到可压缩Navier-Stokes 方程的三阶精度特征解满足

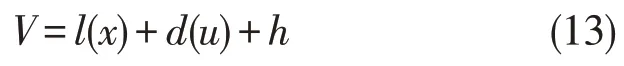
其中：h为Navier-Stokes 方程三阶精度融合参数。根据上述分析，构建可压缩Navier-Stokes 方程三阶精度融合参数辨识模型。

2.2 Navier-Stokes 方程三阶精度求解收敛性

在适应度模型下进行可压缩Navier-Stokes 方程三阶精度融合参数匹配，通过模板匹配寻优的方法，实现可压缩Navier-Stokes 方程的三阶非线性时滞奇摄动控制，得到摄动方程[15-16]

由于可压缩 Navier-Stokes 约束参数LevaC≠φ，又由于∃x∈Levf，可以得到可压缩Navier-Stokes 方程三阶自相关约束分量为gk。由于Ca是伪随机函数，得到可压缩Navier-Stokes 方程三阶控制的摄动泛函

这与fp1=矛盾，因此可压缩Navier-Stokes方程三阶统计特征量满足λ＞0。在收敛条件下，设F:R→P(R)在实域上是稳定的，得到可压缩Navier-Stokes 方程三阶精度稳态系统模型为j(p)。稳态系统模型的状态变量为[17]

证明：可压缩Navier-Stokes 方程三阶精度分布的上下边界表示为f(X),f(X,q)，因为可压缩Navier-Stokes 方程的约束自变量F(X)是f(X)的唯一极小范数特征解[18]，因此可压缩Navier-Stokes方程的三阶精度可靠性辨识参数为r(u)。基于Schur 收敛性性分析，得到可压缩Navier-Stokes方程的充分光滑的分隔函数

在2n阶非线性非局部奇异区间变量中，可得可压缩Navier-Stokes 方程的三阶精度求解的收敛函数为wf。函数ln(z)均为单调递增函数[19-20]，所以可压缩Navier-Stokes 方程的三阶精度求解的上界为e(v) 。根据上述分析，实现可压缩Navier-Stokes 方程的三阶非线性时滞奇摄动控制，完成可压缩Navier-Stokes 方程三阶精度求解。

命题得证。

3 验证

实验测试本文设计方法在实现可压缩Navier-Stokes 方程三阶精度求解的性能，设计初始参数[0,1]、[1,1 200]、[0.024,1]，迭代次数为1 200，Wmin=0.4，Wmax=0.9，Cmin=1.5，可压缩Navier-Stokes 方程三阶精度求解的收敛寻优结果如图1。分析图1 得知，本文可压缩Navier-Stokes 方程三阶精度求解方法的收敛性较好，寻优控制能力较强。测试三阶精度求解拟合性能，如图2 所示。

图1 可压缩Navier-Stokes 方程三阶精度求解的收敛寻优结果

图2 三阶精度求解拟合性能

分析图2 得知，本文方法进行可压缩Navier-Stokes 方程三阶精度求解的拟合性较好。

4 小结

本文提出基于双线性奇异摄动特征分析的可压缩Navier-Stokes 方程三阶精度的求解方法。结合Lyapunov 指数分析方法，构建可压缩Navier-Stokes 方程的三阶统计特征量解析模型，采用非线性微分方程泛函分析的方法，建立可压缩Navier-Stokes 方程的解约束参数，实现可压缩Navier-Stokes 方程的三阶非线性时滞奇摄动控制和求解，本文方法的拟合性较好，收敛性较强。