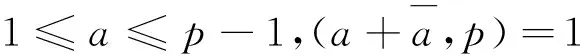一些特殊原根及其分布性质
张 瑾
(西安文理学院 信息工程学院,陕西 西安 710065)
1 引言与主要结果
设p为奇素数,g为整数。如果对所有整数1≤i≠j≤p-1,有(gi-gj,p)=1,则称g为模p的原根[1-2]。众所周知,原根在数论研究中扮演着重要的角色,这是因为若g是模p的一个原根,则g,g2,…,gp-2及gp-1构成模p的一个简化剩余系。这一事实极大地方便了很多数论问题的研究。在这一领域,许多学者研究了原根的基本性质,并得到了不少有意义的研究结果。例如,文献[3]证明了以下结果:设p为足够大的奇素数。则对于任意整数a,b和c满足(abc,p)=1,至少有2个模p的原根α和β,使得同余式aα+bβ≡c(modp)成立。
文献 [4] 证明了更强的结果,由此不难推出更一般的结论:
设p为足够大的奇素数,ui和vi为满足(u1u2v1v2,p)=1的整数。则对任意整数1≤a≠b≤p-1满足(ab,p)=1,存在模p的3个原根α,β和γ,使得以下同余方程成立:
u1α+v1γ≡a(modp)
u2β+v2γ≡b(modp)
有关模p原根和有限域Fq(其中Fq为一个特征为p的q元有限域) 上的本原元的论文可见参考文献[3-19],这里不再一一列举。
本文考虑有关模p原根的如下问题:
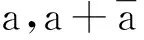
如果成立,令N(p)表示所有这样a的个数。此时,N(p)有哪些渐近性质?
类似地,令M(p)表示所有使得a,a2+1和a2-1为模p原根的a的个数。
本文使用初等方法,特征和及模p原根的特征函数的估计研究N(p)和M(p)的渐近性质,并得到了2个渐近公式,即
定理1对任意奇素数p,有渐近公式
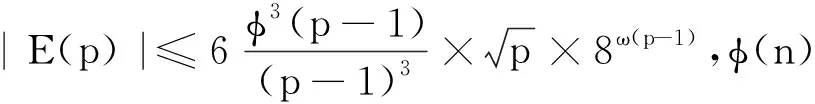
定理2对任意奇素数p,有渐近公式
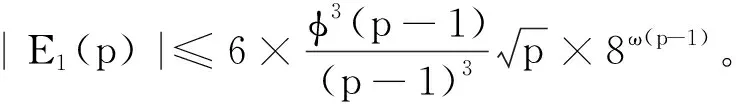
显然定理在有限域Fq中也成立。由定理可得以下2个推论:
推论2设p为充分大的奇素数。则至少存在一个整数1 定理4对任意素数p≡1(mod 4),有渐近公式 由定理3 和定理4 可得以下推论: 推论4设素数p≡1(mod 4)足够大,则至少存在一个无平方因子整数1 在定理3和定理4中,只考虑p≡1(mod 4)的情况。若p≡3(mod 4),无法处理一些特殊特征和的估计,因此不能得到相应的结果。这或许是一个公开的问题。 为了完成主要结果的证明,需要以下几个引理。引理的证明可见参考文献[1-2]。 引理1设p为奇素数,则对任意满足(a,p)=1的整数a,有恒等式 其中e(y)=exp(2πiy),μ(n) 为莫比乌斯函数,且ind(a)为相应于原根gmodp的a的指标。 证明见参考文献[2] 的命题2.2。 引理2设p为奇素数,χ1,…,χr为模p的狄利克莱特征,且至少有一个为模p的非主特征。令f(x) 为一个d次整系数多项式。则对于不同整数对a1,…,ar,有估计 证明见参考文献[20] 的引理17,有关内容见文献[21]。 引理3设p为奇素数,则对模p的任意3个特征χ,ψ和λ(不全为主特征),有估计 (1) 若χ为模p的奇特征,即χ(-1)=-1,则有 (2) 因为3个特征χ,ψ和λ不全为模p的主特征,则由式(1)和式(2)可得引理3。 引理4设p为任意素数,则对模p的主特征χ0,有渐近公式 证明由莫比乌斯函数的性质可得 (3) 即证引理4。 引理5设p为奇素数且p≡1(mod 4),N为满足1 证明因为p≡1(mod 4),则有整数1 (4) 若1 以及估计 可得 (5) 结合式(4)和式(5)可得引理5。 引理6设p为奇素数且p≡1(mod 4)。则对模p的任意3个特征χ,ψ和λ(不全为主特征),有估计 λ(d4a2-1)= V1+V2 (6) 由引理5可得估计 (7) 由估计可得 (8) 结合式(6),(7)和式(8)可得估计 即证引理6。 为简单起见,只证定理1和定理3。类似可得定理2和定理4。 (9) 现分别估计式(9)中的Wi,i=1,2,…,8。显然 (10) 设ω(n)表示n的不同素因子个数。注意 由引理3可得估计 (2ω(p-1)-1)3 (11) 类似地,可得估计 (2ω(p-1)-1)2 (12) (2ω(p-1)-1)2 (13) (2ω(p-1)-1)2 (14) (15) (2ω(p-1)-1) (16) (2ω(p-1)-1) (17) 结合式(9)~(17)可得渐近公式 其中误差项E(p)满足估计 即证定理1。 其中误差项E1(p) 满足估计 即证定理2。 证明(定理3) 由式(9)可得 (18) 由式(18),引理4,引理6及定理1的证明思想,可得渐近公式 即证定理3。 类似地,可推出渐近公式 所有结果得以证明。
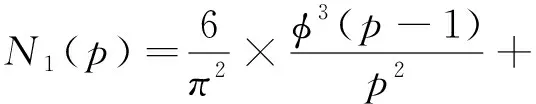
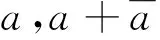
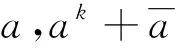
2 引 理
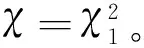
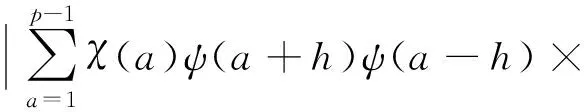
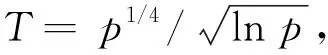
3 定理的证明