基于静力残余力向量的结构损伤评估方法

杨秋伟， 周 聪， 李翠红， 罗 帅

(1.绍兴文理学院 土木工程系，绍兴 312000； 2.宁波工程学院 建筑与交通工程学院，宁波 315211；3.宁波工程学院 浙江省土木工程工业化建造工程技术研究中心,宁波 315211)

1 引 言

有限单元法已广泛用于土木、机械、航空航天、汽车和船舶等众多工程设计领域中，成为解决复杂工程分析计算问题的有效途径。然而，由于大型工程结构的复杂性，用有限元软件建立的结构模型与真实结构总是存在一定的差异，具体体现在，由有限元模型计算所得的结构响应参数(如位移、频率和振型等)总是与仪器测试所得的结构响应参数存在差异。当这种差异较大时，则必须对结构的有限元模型进行修正，确保计算所得与测试所得的响应参数尽可能接近。只有修正后的有限元模型方可用于力学分析与计算。进一步，如果结构中存在损伤，通过修正完好结构的有限元模型来与测试所得的损伤结构的响应参数相匹配，根据模型的修正量就可以判断出结构的损伤单元及损伤程度，这就是基于模型修正的结构损伤识别方法基本原理。近年来，模型修正法和以它为基础的损伤识别方法已成为众多工程技术领域的一项重要课题[1-4]。

残余力向量法[5-16]是一类常用的损伤识别算法，由残余力向量可以判定损伤位置，求解残余力方程可以得到损伤程度。求解方法有最小范数法[5,6]、最小秩法[7,8]或者其他的迭代优化算法[14-18]。目前，已有的残余力向量法都是基于动力测试的模态参数，因此可以统称为动力残余力向量法。和动力测试数据相比，静力测试数据往往精度更高，且无需模态分析等复杂操作，易于实现。因此，本文基于静力测试数据(位移参数)，结合有限元刚度矩阵，定义了静力残余力向量，根据其中不为零的元素来判断损伤自由度，再根据自由度和单元之间的对应关系来确定损伤位置，在此基础上，提出一种求解损伤参数的代数解法。另外，鉴于梁、刚架或实体结构中节点角位移难以测量的情况，进一步提出了一种静力缩聚残余力向量法，只需要应用节点线位移数据，从而有效拓宽了所提方法的应用范围。数值算例结果说明所提方法合理有效。

2 静力残余力向量法

一般而言，结构的损伤主要导致结构刚度的变化，质量的变化基本可以忽略不计。不失一般性，假设K0和K分别为结构损伤前后的刚度矩阵(n×n维)，由于损伤所导致的刚度损失量为ΔK，即

(1)

式中Ki为第i个单元刚度矩阵，αi为第i个单元的损伤参数(αi∈[0,1])，αi=0表示第i个单元未损伤，αi=1表示第i个单元完全损伤，N为单元体总数目。结构损伤前后，在荷载向量l作用下的位移向量分别为

K0d0=l, (K0-ΔK)d=l

(2,3)

式中d0和d分别为完好结构和损伤结构的位移向量，其可以通过静力测试得到。由方程(3)变形可得

ΔK·d={δ}， {δ}=K0d-l

(4，5)

方程(4)即为静力残余力方程，其中向量{δ}称为静力残余力向量，由方程(5)可知，只要测试获得损伤结构在已知荷载向量l作用下的位移d，即可由方程(5)计算得出其静力残余力向量。根据方程(4)，由静力残余力向量{δ}来进行损伤定位的原理在于，结构损伤一般只导致ΔK的少数行向量不为零，即和损伤对应的自由度所在的行向量不为零，因此，静力残余力向量{δ}中不为零的元素即对应着损伤自由度，由损伤自由度并根据几何关系即可确定发生损伤的具体单元。具体而言，可将方程(4)改写为以下方程组，

(6)

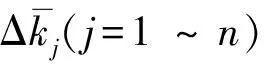
当损伤位置由上述方法判定出来以后，结合方程(1，6)，可以进一步求解损伤程度，即求解损伤参数αi。分两种情况讨论。

首先讨论单个损伤情况，如果由静力残余力向量{δ}判定出来只有一个单元体发生损伤，则只有一个未知的损伤参数αi需要求解，此时方程(1)简化为

ΔK=αiKi

(7)

相应地，方程(6)简化为

(8)

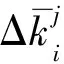
(9)

方程(9)中δj取{δ}的任意一个非零元素即可。

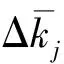
(10)

方程(10)代入式(6)整理可得

Π{αi}′={δ}′

(11)

式中Π为整理所得的系数矩阵，{αi}′为q个未知损伤参数组成的列向量，{δ}′为q个非零的δj组成的列向量。由方程(11)即可求得损伤程度为

{αi}′=Π-1{δ}′

(12)

对于梁、刚架和实体结构，其节点位移既有线位移也有角位移，实践中由于角位移难以测量，上述的静力残余力向量法需要进一步改良方可使用。为此，本文采用模型缩聚来对这些角位移进行缩减处理，从而使得缩聚后的相关公式都只包含各节点线位移，拓宽了静力残余力向量法的应用范围。缩聚方法具体过程如下。

首先,将结构的全部自由度分为平动自由度(保留自由度)和转动自由度(缩减自由度)两类，相应地将方程(2)改写为

(13)

式中上标m和s分别表示平动自由度和转动自由度，m和s同时也表示平动自由度和转动自由度的数目。若所有的转动自由度上均未施加外荷载，即ls=0，则由方程(13)的第二行可得

(14)

由方程(14)可得

(15)

(16，17)

式中矩阵Θ为自由度转换矩阵。将方程(16)代入式(13)，并两边左乘ΘT可得

Krdm=lr,Kr=ΘTK0Θ,lr=ΘTl

(18～20)

利用方程(18)缩聚后的刚度矩阵和荷载向量，按照前述静力残余力向量同样的推导过程，可推导得到缩聚后的残余力向量计算公式如下，

{δ}r=Krdm-lr

(21)

式中Kr为完好结构缩聚后的刚度矩阵，lr为缩聚后的荷载向量，dm为损伤后结构各平动自由度处的线位移向量。相应地，也可以得到模型缩聚后类似于方程(9，12)的计算损伤程度公式为

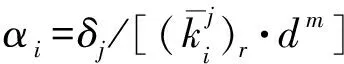
(22)

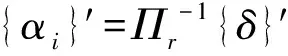
(23)

3 数值算例

3.1 桁架结构

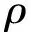
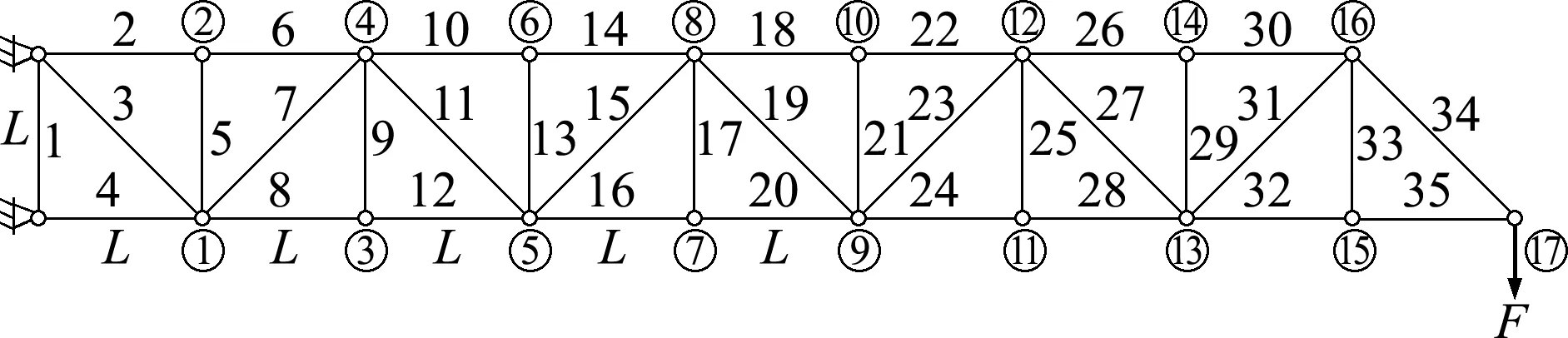
图1 桁架结构及静力加载

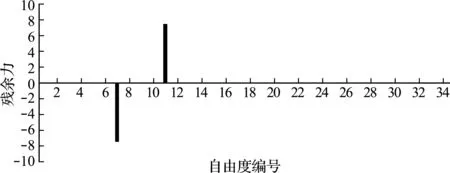
图2 单元10损伤时的静力残余力向量(单位：kN)

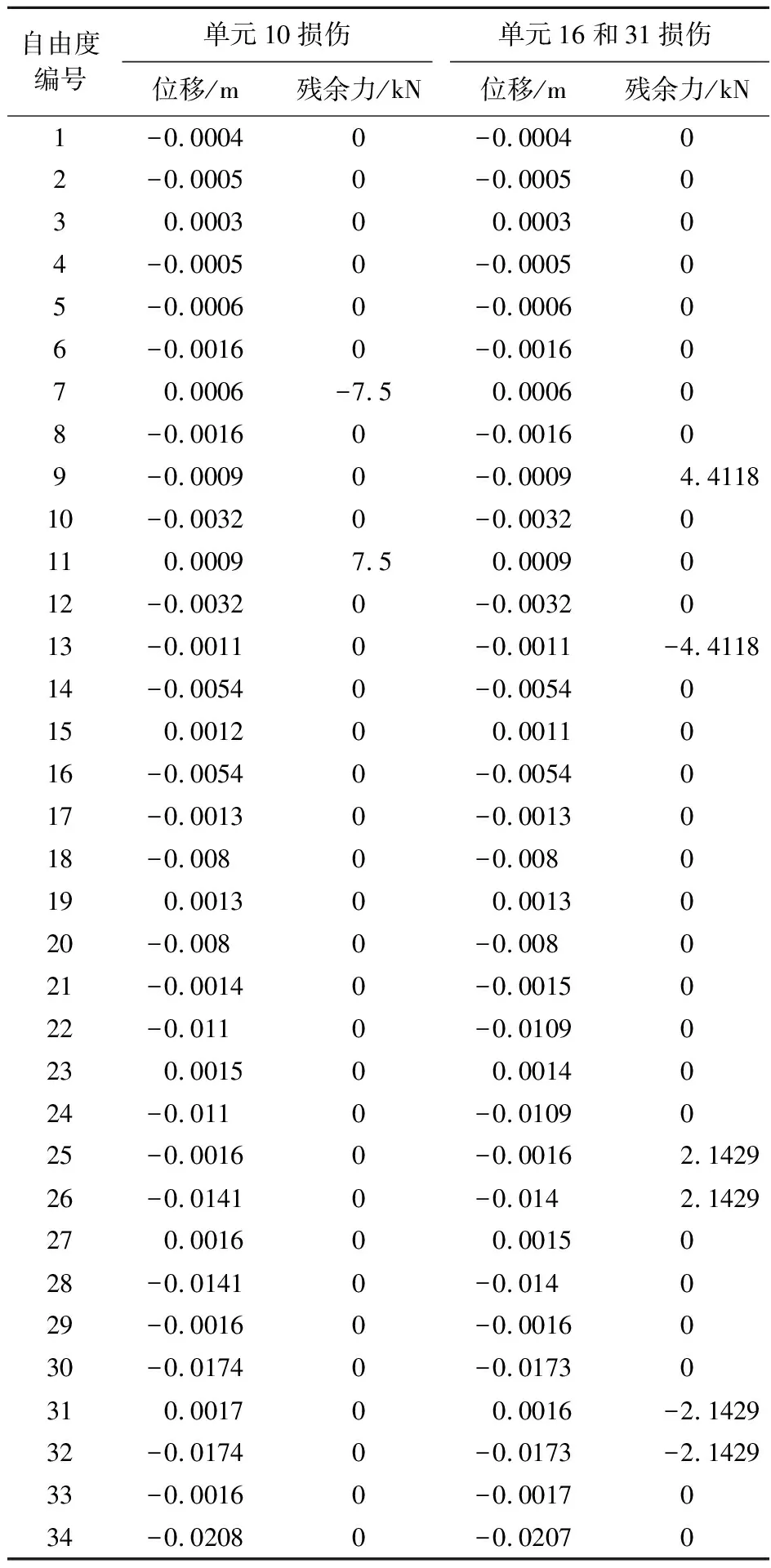
表1 损伤结构位移和残余力向量计算结果

接下来讨论多个损伤情况，不失一般性，假设单元16和31刚度分别损伤15%和30%，这种情况下损伤结构的位移数据和残余力向量分别列于表1的第4列和第5列，为了更直观，将表1的第5列数据绘入图3。可以看出，残余力不为零的自由度编号为9/13，25/26/31/32，根据图1，自由度9和13对应的节点为第5和第7号节点，显然，这两个节点之间的杆件刚好为单元16，而自由度25/26/31/32分别对应着13和16号节点，这两个节点之间为单元31。因此，根据残余力向量中不为零的元素最终可以判定单元16和31为发生损伤的单元。接下来计算损伤程度，由于欲求的损伤参数个数为2，需要列两个方程(方程(11))，这里选择第9个自由度(对应损伤单元16)和第32个自由度(对应损伤单元31)来列方程，方程(11)的具体计算结果为

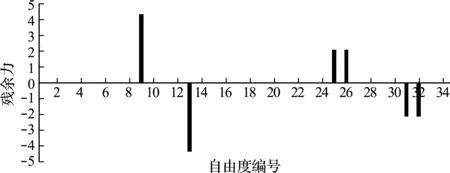
图3 单元16和31损伤时的静力残余力向量(单位：kN)

(24)

进一步由方程(24)计算可得损伤参数为α16=0.15和α31=0.3，刚好与假设值15%和30%相等。

需要说明的是，在上述模拟过程中，并未考虑有限元模型误差与测试数据误差，因此计算所得的损伤程度值和假设值完全相等，这也直观地说明了本文所提的损伤程度代数解是一种理论上的精确解。如果考虑数据误差，如对于单元10损伤情况，在损伤结构各个位移数据中添加误差水平为3%的随机数，则可得静力残余力向量如图4所示，可以看出第7和第11自由度(对应单元10)处残余力明显偏大，故仍然可以判断单元10为损伤单元，其损伤程度计算值为0.1989，与假设值0.2很接近。如果有些情况难以根据残余力向量图形做出准确的损伤定位，可以结合残余力向量图形和损伤程度计算结果来综合进行判定，具体见接下来的梁结构算例。

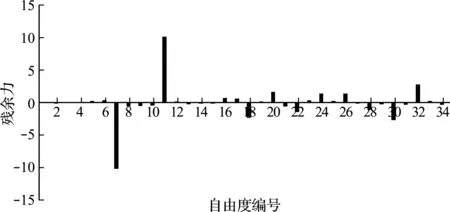
图4 利用含噪声数据计算所得静力残余力向量(单元10损伤，单位：kN)

3.2 梁结构

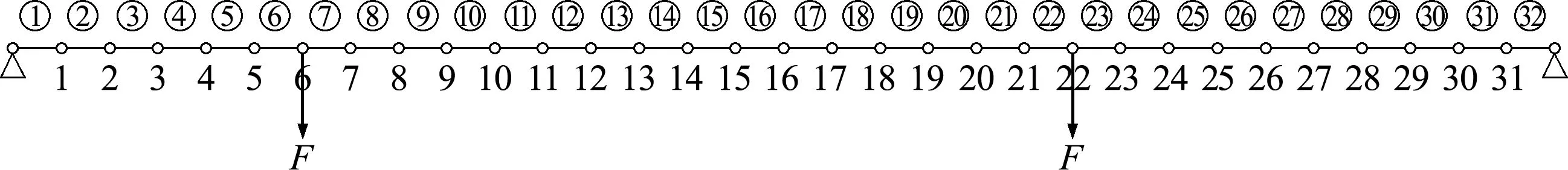
图5 梁结构

不失一般性，假设单元15刚度损伤20%，图6给出了无噪声时静力缩聚残余力向量的计算结果。可以看出，绝对值偏大的残余力集中于节点13，14，15和16处。根据单元体和平动自由度编号之间的对应关系，位于这4个节点之间的是第14，15和16号单元。由此可见，采用静力缩聚残余力向量，由于模型缩聚所带来的误差，不能精确定位于真正发生损伤的第15号单元处，而是定位于以损伤单元为中心的局部小区域。为了进一步准确判断，分别计算第14，15和16号单元的损伤程度值。首先，计算第14号单元，该单元对应的节点编号为13和14，这里采用节点13对应的残余力来进行计算(由于节点14的残余力可能由于第14号单元或第15号单元引起，故此处不宜采用节点14)，所得结果为α14=-0.3581，据此判断第14号单元并非真正损伤单元。接下来，计算第16号单元，该单元对应的节点编号为15和16，这里采用节点16对应的残余力进行计算，结果为α16=-0.3402，据此判断第16号单元也并非真正损伤单元。最后，计算第15号单元，该单元对应的节点编号为14和15，为了可靠起见，分别采用这两个节点处残余力对应的方程来进行计算，所得结果分别为α15=0.2156(节点14)和α15=0.2159(节点15)，这两个结果均说明第15号单元为真正损伤单元，损伤程度计算值可取为二者的平均值，显然与假设值0.2很接近。考虑在位移数据中添加3%噪声水平的随机数，所得静力缩聚残余力向量如图7所示，可见绝对值偏大的残余力仍然集中于节点13，14，15和16处，利用和上述相同的损伤程度计算过程，所得结果分别为α14=-0.3005，α16=-0.3714，α15=0.2012(节点14)和α15=0.2235(节点15)，故仍然可以判定出第15号单元为损伤单元，说明所提的静力缩聚残余力向量法是合理可行的。

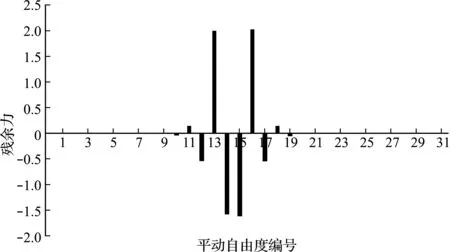
图6 无噪声时静力缩聚残余力向量(单元15损伤，单位：kN)

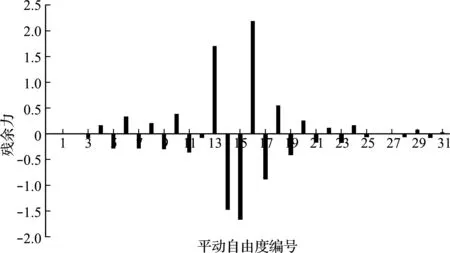
图7 有噪声时静力缩聚残余力向量(单元15损伤，单位：kN)

4 结 论

提出一种静力残余力向量法用于结构损伤评估，利用结构静力测试数据和有限元模型刚度矩阵，根据静力残余力向量中不为零的元素来判断损伤自由度；再根据自由度和单元之间的对应关系来确定发生损伤的位置，并提出一种求解损伤参数的代数解法；另外，针对实践中角位移难以测量的情况，进一步提出了一种静力缩聚残余力向量法，有效拓宽了所提方法的应用范围。数值算例结果表明，所提方法合理可行，对单个损伤和多个损伤情况均可适用，可为解决结构损伤识别问题提供参考。