强放射性环境用气压传感器的管路与压力响应分析

李 海，王时龙，易力力，安 然，龚金龙

(1.重庆大学 机械传动国家重点实验室，重庆 400044；2.中国原子能科学研究院，北京 102413)

引言

在强放射性环境中使用的仪控设备不允许使用电气元件，气动元件结构简单，使用方便，具有防爆、可靠性高等优势[1]。强放射性环境用气压传感器的原理是将泄压单向阀设置在强放射性环境中，气源控制部分和气压表放置在正常环境中，通过耐辐照的长气管连接单向阀和气源控制部分。气压传感器设置在设备的固定位置，其泄压单向阀可被设备执行机构打开/闭合。在正常工况下，长气管内充满气体并保持恒压；在执行机构打开泄压单向阀后，位于正常环境中的气压表会发生压力变化，以此判断执行机构的动作位置并反馈给控制系统，实现气动元件的闭环控制[2]。由于从放射性环境引出到正常环境中的长气管大概需要几十米长，而气体具有可压缩特性[3]，气压信号在传导过程中会出现滞后和稳定性较差的问题，影响气压传感器的应用。因此，研究气压传感器的滞后性原因，得出其滞后性能是工程应用的必要环节。

1 试验设备和仪器

通过设计试验装置可得到特定气压传感器的气压信号延迟特性，该试验装置的外形见图1。试验装置的主要构成为气动三联件、可调节流量阀、气压传感器、位置传感器、直线模组、带顶升机构的单向阀、PLC系统和计算机，采用PLC系统采集气压和位置信号[4]。

图1 气动试验装置

气体经过气动三联件[5]处理，首先气体将充满初始状态的气体管路，单向阀处于闭合状态，压力表压力保持不变，控制系统对顶升机构的运动件发出运行信号，运动件开始位移，当运动件到达触动单向阀阀芯处，同时触发位移传感器记录时间点和位移点，单向阀处于开启状态后，压力开始下降，当压力表刚好下降到额定气压时，气压传感器记录时间点和位移点，两点的差值就可以得到信号滞后的时间和位移。运行3000次前后信号滞后的时间和位移相比较，就可以验证机构的稳定性，试验原理图如图2所示。

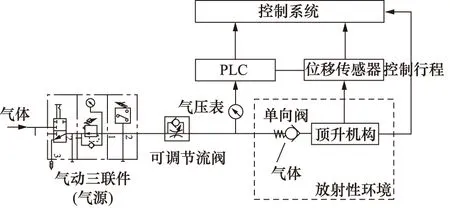
图2 气动装置原理图

试验条件：试验温度为20 ℃，试验进口处压力为0.6 MPa，单向阀出口处压力为0.2 MPa；试验气管长度为20，30，50 m；气管内径为5.5 mm。

2 试验数据

首先组装好试验装置，选用20 m气管做为气管回路。调节好流量计，使气压达到稳定压力值0.6 MPa。调整顶升装置的运动件按照不同的运动速度6, 10, 20 mm/s向前运动，到达指定位置后开始记录时间点，并从气压传感器测得气门开关释放气流后稳定到压力值0.2 MPa的时间点，记入PLC中。如此重复10次，记录3组不同速度的响应时间数据，然后再分别换30 m 和50 m气管进行试验。不同速度的试验数据记录及处理见图3～图5，可以看出，随着气管长度增加，气门传感器的滞后时间明显增加。

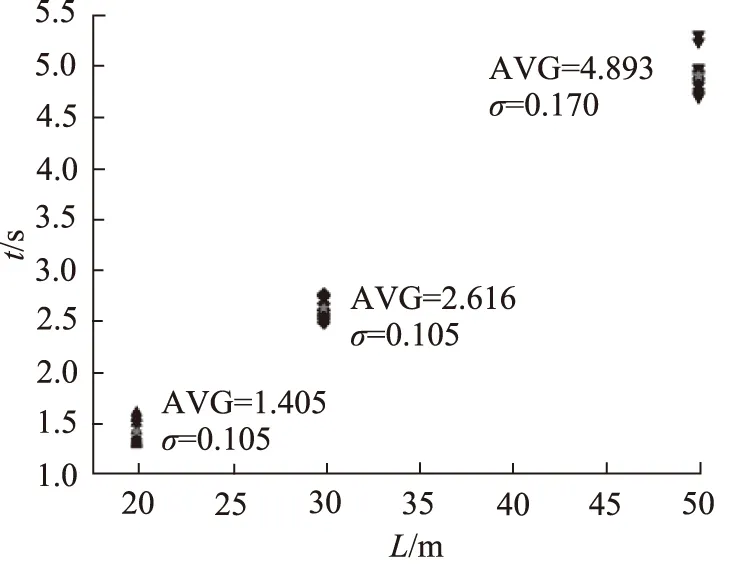
图3 6 mm/s的延迟数据图

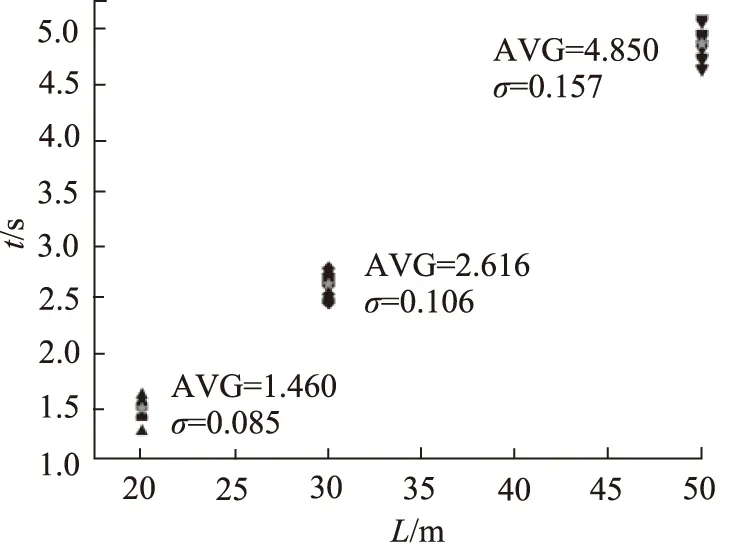
图4 10 mm/s的延迟数据图

图5 20 mm/s的延迟数据图

3 影响因素

首先，对整个试验装置可能的延时滞后因素进行分析，得出主要影响因素为：

(1) 气压传感器、位移传感器的响应时间；

(2) 长气管回路的充排气响应时间；

(3) 单向阀的阀芯开启速度。

气压传感器、位移传感器均采用标准型传感器，响应时间均为毫秒级别，滞后时间可忽略不计。

长气管回路的充排气响应时间，查阅相关资料，可采用气管回路的排气特性公式进行计算。气阻元件单向阀的选型和气路长度已固化，对恒定压力的气体通过固定气体节流装置，其气阻不变，然后向固定体积的气体回路进行充排气[6-7]。因此该充排气体模型为定气阻、定气容模型。气体的排气时间的特性公式为：

当ε=p/ps≤0.528时(即音速流状态)：

[(p/ps)-(p0/ps)]

(1)

当ε=p/ps>0.528时(即亚音速状态)：

(2)

式中，t1,t2—— 排气时间

V—— 气容容积

ps—— 恒定气源压力

p0—— 气容内初始压力(t=0)

p—— 气容充气任意瞬时的压力

Csfs—— 气阻节流孔口有效截面积[8]

K—— 绝热指数(K=1.4)

R —— 气体常数

Ts—— 恒压气源气体温度

通过式(1)和式(2)，可得出不同气管长度回路的理论排气时间。单向阀带有顶升机构，不同的运动速度影响阀芯开启速度，阀芯开启速度也影响气回路的排气速率。本实验采用运行速度10 mm/s进行试验。通过对单向阀结构分析，顶升装置从阀体开始打开(即发出信号)到阀体完全打开有约1 mm的行程，在阀体开启过程中，气体的充排气模型为变气阻、定气容模型，对式(1)进行修正。Csfs可分为两部分：

(1) 芯体从关闭到打开时，气阻节流孔有效截面积的变化函数Csfs=fst/t0，其中fs为完全打开时的截面积，t为阀体开启时间，t0为完全打开时的时间；

(2) 芯体完全打开时，有效截面积为常数。对公式修正后，计算出理论分析时间。其中，在运动速度为6 mm/s时，受阀芯开启速度影响滞后约0.17 s。表1为速度6 mm/s时的理论计算时间和试验时间。

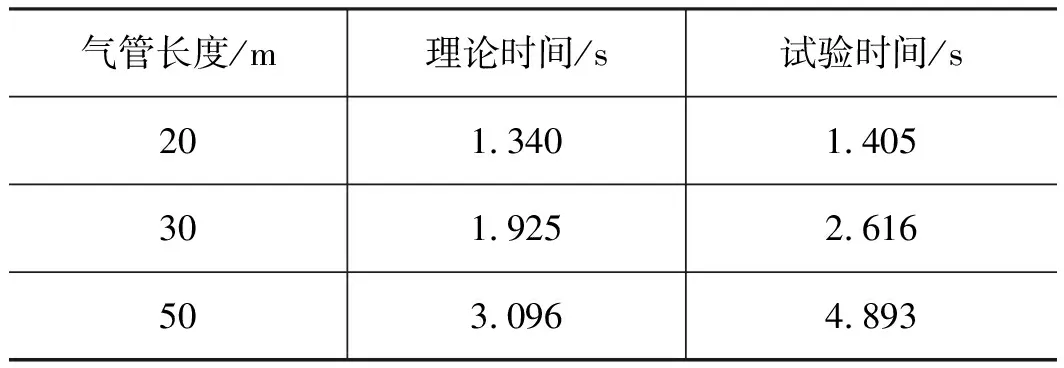
表1 不同气管长度回路的理论时间和试验时间

可以看出，随着本试验装置的气管长度增大，理论计算值与试验值的差距呈线性增长，理论充气特性公式与实际气管内试验结果有差异。因此，对理论充气特性公式的适用范围进行分析。

首先对气管内的空气进行动力学分析，查阅相关表[9]，空气动力黏度μ为18.34×10-6Pa·s，密度ρ为7.0146 kg/m3，在气体管路内气压由0.6 MPa下降到0.2 MPa时，经计算，气体雷诺数Re=710411>4000，在气管内处于紊流状态，流体质点的速度和大小都在不停变化。空气在向前流动时，会存在各个方向的脉动，造成对管壁构成附加阻力，不同管道长度会使气体流速产生不同的变化，从而产生不同的阻尼比，属于非线性状态。经调研相关文献，使用理论公式的装置模型气管回路体积V约为30×10-6m3，本研究中最小的30 m气管体积为475×10-6m3。因此本研究使用的气管模型的阻尼比更大，理论公式无法覆盖气管模型，需要调整阻尼比来拟合试验数据。

4 长气管模型

气体在长气管内会产生沿程压力损失，沿程压力损失与位移在总体趋势上呈正比关系，但在紊流状态下，沿程阻力系数与管径和速度都有关，多为经验公式。本长气管模型是一个过程变阻尼比的质量-弹簧模型[10]，如图6所示。本试验装置的气管模型中存在：气体质量M、气体刚度KL、气管阻尼比β、外部压力F(t)。

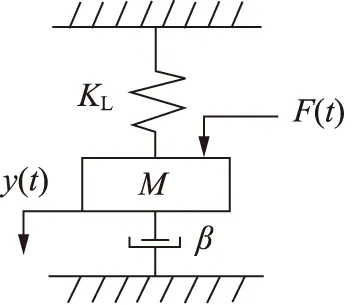
图6 质量-弹簧模型

其传递函数为：

(3)

式中，F(t) —— 外部压力函数

β—— 阻尼比

y(t) —— 弹簧位移函数

KL—— 气体弹簧刚度

可以看出，气体的传递函数为一个典型的由增益、振荡和延迟环节组成的函数，在外部压力恒定的情况下，对该函数进行拉普拉斯变化，可得到长气管传递模型为[11]：

(4)

式中，wn为系统自振角频率。

根据试验数据可以看出，在气管长度为20～50 m范围内，当响应时间超过1 s后，气管模型的延时随气管长度呈非线性增长分布。这是因为，其阻尼比β大于1后，与响应时间TL非振荡关系，变为阶跃惯性增长关系。其传递函数为：

(5)

式中，TL—— 时间常数

T—— 当β=1时的时间常数

a—— 常数

其响应曲线如图7所示。

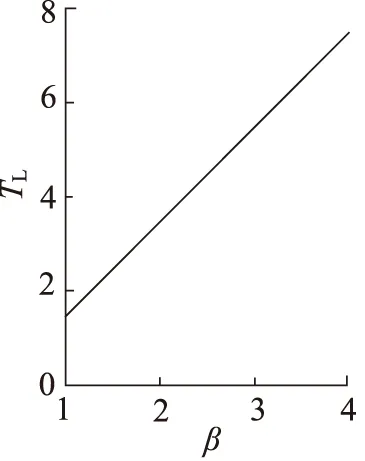
图7 阻尼比与时间常数的响应曲线

当β≥2时，位移y(s)与阻尼比β的关系可采用惯性传递，简化为[12]：

(6)

理论上，式(2)只适用于气容较小的情况，其沿程阻力系数只作为常数考虑，这种模型并不适用长气管模型。实际的沿程压力损失会随着气管长度增加呈加速增长趋势，其阻尼比(沿程阻力系数)为惯性增长函数。因此，将理论公式和实验数据进行修正和拟合，将式(2)变为阻尼比随长度增长的二次函数，优化为：

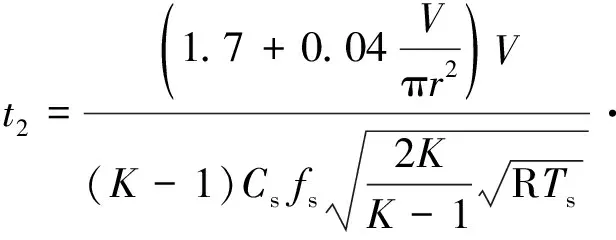
(7)

式中，r为气管半径，m。

表2为不同气管长度回路的试验时间、理论分析时间和优化后的理论分析时间对比表。图8为不同气管长度回路的压力-时间响应试验曲线。可以看出，优化后的理论分析时间与试验数据更吻合，也符合理论分析。

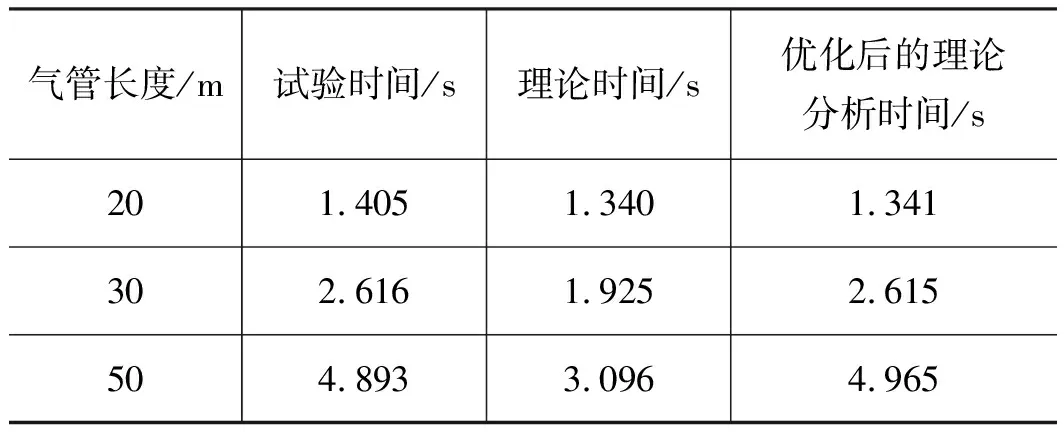
表2 时间对比表

图8 不同气管长度回路的压力-时间响应试验曲线

5 结论

(1) 在大容积的条件下，线性增长的气体排气公式不适用于远距离传输的气压传感器，气压传感器的管路长度与气压响应时间需要通过试验装置进行验证，根据不同的试验数据对理论公式进行优化；

(2) 实验数据表明：在长气管模型下，气体在气管内的阻尼比(沿程阻力系数)为惯性增长函数，气压响应时间与气管长度呈非线性、加速增长趋势；

(3) 在传输距离一定的情况下，可减少节流件数量、增加单向阀气流孔有效截面、气管拐弯数量等手段，目的是减小长气管回路的气阻，以提高气压传感器的灵敏度。