挥发性油藏原油采收率预测的改进方法
鹿克峰,苏畅,程超逸
(中海石油(中国)有限公司上海分公司勘探开发研究院,上海 200335)
0 引言
挥发性油藏的气油比通常为 267~623 m3/m3,原油体积系数大于1.8,在泡点压力以下具有高收缩率;通常认为衰竭式开采的挥发性油藏采收率不高,一般为19%~25%[1]。为避免原油收缩,多数挥发性油藏采用注气、注水保压或混相驱开发。一些实际开发案例显示,采用衰竭式开发的挥发性油藏实际原油采收率高于预测值。1978年投入开发的美国波德河盆地Buck Draw油田属弱挥发性油藏,低于饱和压力的情况下产量递减趋势没有明显增大,李国玉等[2]认为游离气中的凝析油延缓了产量的递减;中国渤海海域BZ13-1属近饱和挥发性油藏,受海上平台限制采用衰竭式开发,生产过程中气油比始终呈平稳上升趋势,在地层压降幅度为 40%时,原油采收率达 22%,超过最终采收率预测值[3];中国南海西部油田ZH1-2L挥发性油藏,采用衰竭式开发,地层压力低于原始泡点压力后气油比未出现快速上升趋势,在地层压降幅度为 35%时,原油采出程度达到 20%[4]。以上生产现象均说明,传统的挥发油采收率预测方法存在一定的问题。
针对衰竭式开发的饱和油藏,通常基于传统溶解气驱油理论预测采收率,应用较为广泛的Muskat法[5]、Schilthius法[6]以及 Tarner法[7]均假设油藏存在油气两相,且两相间不存在相间传质。事实上,由于挥发性原油中间组分占比高,衰竭开发过程中必然存在相间传质,传统溶解气驱油理论预测挥发油采收率的适用性有待落实。针对挥发性油藏的油藏工程方法研究始于 1974年,Cook等[8]和 Coats[9]提出了挥发油气比的概念,可通过挥发性油样等容衰竭实验测量;1986年,Fetkovich等[10-11]应用挥发油气比的概念,推导出挥发性油藏或凝析气藏气油相对渗透率比值的计算公式;1994年,Walsh等[12-13]进一步推导出广义物质平衡方程。前人的研究为挥发性油藏采收率预测奠定了一定的基础,但尚未形成完整的方法体系。
原油多次脱气实验测取的原油物性参数,不能直接用于评估挥发油的采收率。具体原因如下:①妥宏等[14-16]指出多次脱气实验是以油气两相保持稳定、不发生相间传质为前提,实验原理不适用于挥发性油藏;②吴克柳等[17-19]认为单次或多次脱气实验过程中,过高的压降速率和压降幅度易导致挥发油非平衡油气分离,使实验数据产生偏差。针对实验原理引起的实验数据偏差,鹿克峰等[20]提出结合等容衰竭实验数据矫正多次脱气实验数据的方法,并给出了相应的矫正公式。
为描述挥发性油藏衰竭开发过程中复杂的相态转换,本文定义 4个流体转换相态(液态油、液态气、气态气、气态油),并依据地面体积平衡原理实现分相产量与分相剩余储量分离,进而考虑脱出溶解气中凝析油含量的影响,改进挥发性油藏传统溶解气驱油理论采收率预测计算方法;结合单次脱气、等容衰竭、多次脱气实验,建立多次脱气实验数据矫正方法。
1 常规油藏工程方法的局限性
1.1 多次脱气实验方法的局限性
从渤海BZ13-1油田BZ13-2井、渤海BZ13-1油田BZ13-1-A4井、东海平北WYT构造NB19-6-2井、西非AKPO油藏Akpo 2井、东海西湖凹陷CX油藏CX-4井中各提取 1个油样。5个油样的 PVT(压力-体积-温度)实验数据如表 1所示,油样各项参数间存在关联性:饱和压力下,单次脱气测定的溶解气油比越高,其原油体积系数越高,多次脱气测定的原油体积系数和溶解气油比也越高。以单次脱气测定的溶解气油比作为衡量指标,将 5个油样依次定性为强挥发性原油(样品1、样品2)、中—弱挥发性原油(样品3、样品4)、典型黑油(样品5),实验温度分别为166,166,119,85,110 ℃。总体上,油样挥发性越强,饱和压力下,单次脱气与多次脱气测定的原油体积系数、溶解气油比差异越大,等容衰竭实验测定的脱出溶解气中的凝析油含量也越高。

表1 典型原油PVT实验数据
单次脱气实验始终处于封闭容器中,没有油量损失;多次脱气实验排气过程中,溶解气中的凝析油伴随脱出气体一起被排出,并不包含在最终回收的油量中,因此在实验达到油气相态平衡时,饱和压力下,多次脱气原油体积系数及溶解气油比会高于单次脱气。然而实际油藏开发过程中,脱出溶解气中的凝析油,部分伴随自由气相产出被地面回收,部分再次反凝析并伴随自由液相产出被地面回收,部分滞留在油藏中,从油藏到地面设备没有凝析油外泄。因此,多次脱气实验数据不能直接用于挥发性油藏,需要对实验数据进行矫正。
1.2 传统溶解气驱理论的局限性
针对废弃压力高于泡点压力的封闭型油藏,开发过程中地层无溶解气脱出,可直接采用未饱和油藏物质平衡方程估算基于原油本身弹性膨胀的原油采收率[21]:
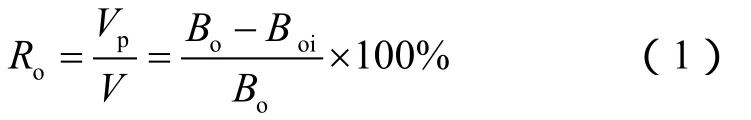
对于饱和油藏,因开发过程中储集层出现油气两相,通常采用传统的溶解气驱油理论预测采收率[7],其中包含 3个基本方程,即经典溶解气驱油藏物质平衡方程、原油饱和度预测方程、瞬时生产气油比预测方程,分别如(2)式—(5)式所示:

累计生产气油比预测方程为:
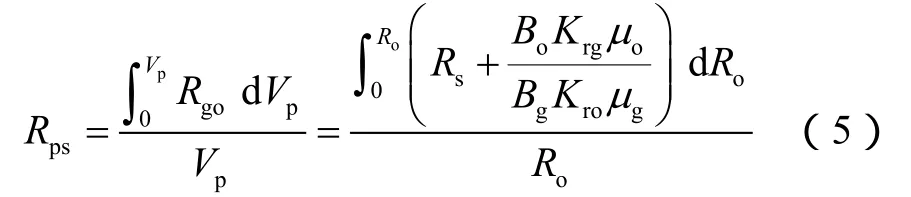
联立(2)式、(3)式及(5)式,以累计生产气油比Rps为迭代目标,预测原油采收率。
传统溶解气驱油理论涉及的基本方程中缺少凝析油含量项,表示脱出的溶解气为干气,这与挥发性原油PVT等容衰竭实验脱出的溶解气中含有凝析油的事实不符,直接采用该理论预测挥发性油藏采收率会低估原油采收率,需要改进计算方法。综上,采用常规油藏工程方法预测挥发性油藏采收率,需要矫正多次脱气实验数据并对传统溶解气驱油理论进行改进,二者均需要考虑脱出溶解气中的凝析油含量。
2 原油采收率预测方法改进
考虑挥发性油藏脱出的溶解气中凝析油含量对挥发性原油采收率的影响,分别从计算方法和实验数据矫正两个方面展开研究,改进传统溶解气驱油理论的3个基本方程式,建立多次脱气实验数据的矫正公式。
2.1 分相剩余体积和分相产量分离
随着挥发性油藏的开采,在地层压力降至泡点压力时,油藏中剩余烃类流体由单一油相转变为自由油相和自由气相,且自由油相中含有溶解气,自由气相中含有凝析油。因此,地面产出油应来自油藏中的油、气两相,地面产出气来源类同。为清晰描述挥发性油藏地下与地面流体相态之间的转换关系,定义 4个流体转换相:液态油、液态气、气态气、气态油。液态油和液态气表示在油藏中呈油相,在地面分别转换为油相和气相的组分;气态气和气态油表示在油藏中呈气相,在地面分别转换为气相和油相的组分。将 4个转化相体积定义为地面标准状态下的体积,依据地面体积平衡原理,计算分相剩余体积和分相地面产量。
2.1.1 剩余液态油体积和剩余气态气体积计算
在原始状况下,油藏中呈单相油状态,原始液态油体积即为原油储量Vfoi,原始液态气体积即为溶解气储量,可表示为VfoiRsi。在地层压力降至泡点压力以下时,油藏中存在两相,油藏中剩余液态油体积以Vfo表示,则剩余液态气体积可表示为VfoRs;油藏中剩余气态气体积以Vfg表示,则剩余气态油体积可表示为VfgRv,若累计产油量为Vp,则累计产气量为VpRps。
依据地面油、气相体积平衡原理:油藏剩余液态油体积与油藏剩余气态油体积之和等于原始液态油体积与累计产油量之差;油藏剩余气态气体积与油藏剩余液态气体积之和等于原始液态气体积与累计产气量之差,可得:
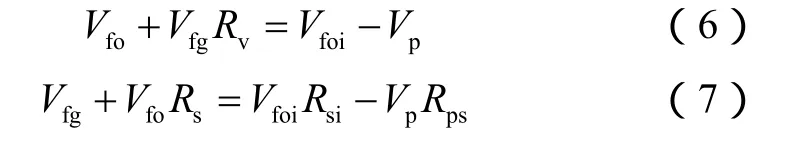
联合(6)式和(7)式,可得到剩余液态油体积和剩余气态气体积:
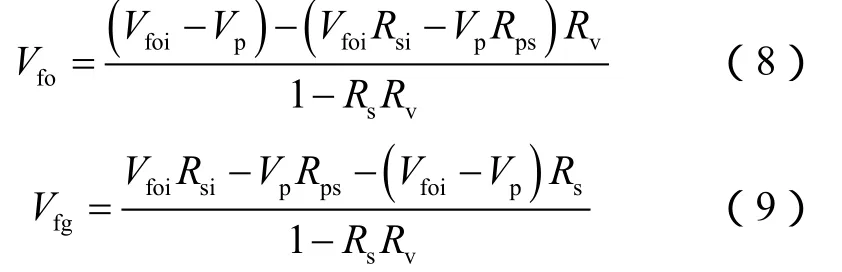
2.1.2 气态气与液态油瞬时产量计算
在地层压力降至泡点压力以下时,设油藏中瞬时气态气产量为qfg,瞬时液态油产量为qfo,则瞬时气态油产量为qfgRv,瞬时液态气产量为qfoRs。若现场计量的油藏瞬时总产气量为qg,瞬时总产油量为qo,依据地面体积平衡原理,可以得到:联合(10)式和(11)式,得到液态油和气态气的瞬时产量:

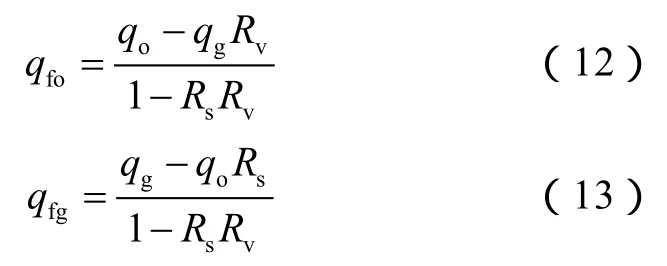
2.2 传统溶解气驱油理论的改进
2.2.1 挥发性油藏物质平衡方程
在地层压力低于泡点压力后,挥发性油藏满足地层体积平衡(封闭油藏,不考虑水侵):原始总烃类孔隙体积等于目前油相占据的孔隙体积与目前气相占据的孔隙体积之和,即:
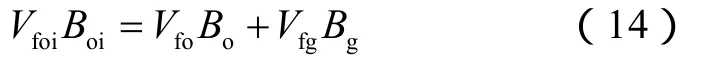
将(8)式、(9)式代入(14)式:
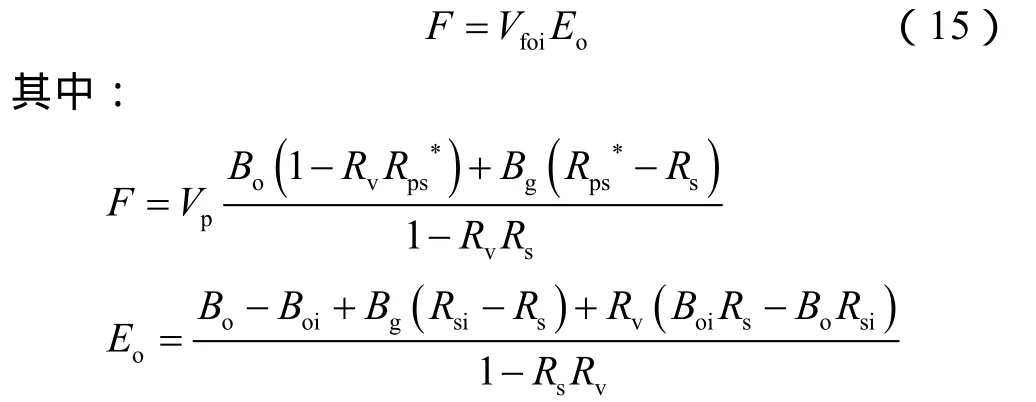
(15)式即为封闭型挥发性油藏物质平衡方程式,整体上与Havlena-Odeh提出的经典线性物质平衡方程具有相同形式[22-23],物理意义为原油储量的弹性膨胀量等于累计产出烃类地下体积,但前者同时考虑到气态油和液态气的影响,后者仅考虑到液态气的影响。将F计算式代入(15)式,整理出原油采收率的计算公式:

(16)式是考虑了脱出溶解气中凝析油含量,对传统溶解气驱油藏采收率预测方法中(2)式的改进。
2.2.2 挥发性油藏原油饱和度预测方程
油藏原油饱和度可表示为目前油相占据的孔隙体积与油藏总孔隙体积之比:
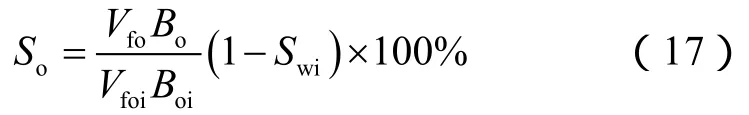
将(8)式和Ro*=Vp/Vfoi代入(17)式,得到:

(18)式为考虑脱出溶解气中凝析油含量,对传统溶解气驱油藏采收率预测方法中(3)式的改进。
2.2.3 挥发性油藏生产气油比方程
油藏中自由油相的瞬时流量应等于液态油瞬时产量乘以原油体积系数,而不是由现场计量的瞬时总产油量折算而来,自由气相类同。由气、油两相达西定律比值可得到:

将(12)式、(13)式代入(19)式,且等式左边分子分母同时除以qo,整理得到瞬时生产气油比(Rgo*=qg/qo)计算公式:
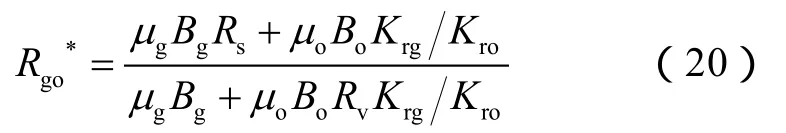
(20)式对原油采收率积分可得到单位原油储量下的累计产气量,进而实现累计生产气油比计算公式:
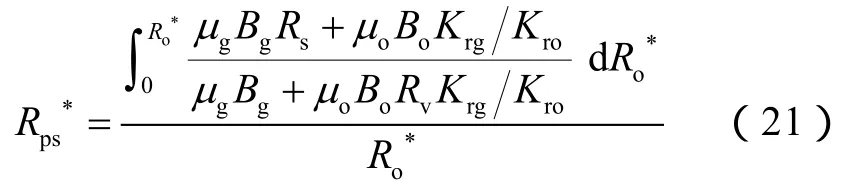
(21)式即是考虑脱出溶解气中凝析油含量的影响,对传统溶解气驱油藏采收率预测方法中(5)式的改进。
(16)式、(18)式、(21)式组成全新的溶解气驱挥发性油藏原油采收率预测方程组,若已知油藏流体PVT数据、油气相对渗透率曲线,可通过迭代法实现油藏采收率预测,具体分 4个步骤:①设定油藏初始压降,计算流体高压物性参数,此时(16)式中存在两个未知量Ro*、Rps*,需先假定一个Rps*值,计算出原油采收率Ro*;②将步骤①假定的Rps*值以及计算的原油采收率Ro*代入(18)式,计算出So*;③将步骤②计算的So*通过气油相对渗透率曲线标定,可得到Krg/Kro,进而代入(21)式计算出累计生产气油比;④步骤③计算的累计生产气油比与步骤①假定值不一定相等,通过反复迭代,直到假定值与计算值一致,此时计算的原油采收率即为所求值。通过同样步骤,可预测后续不同衰竭压力下对应的原油采收率。
2.3 多次脱气实验数据矫正方法
原油的多次脱气实验是在地层温度下,循环进行多次的降压脱气-等压放气过程,每次循环后测量钢瓶中原油体积以及放出气量,并记录最终标准状况下的残余油体积,依据测量数据计算原油的高压物性。因实验过程中不测量也不考虑放出气中所含油量(气态油),实验计算的原油体积系数和溶解气油比会明显偏高。但结合等容衰竭实验中测取的气态油含量,可以依据地面体积平衡原理求得不同衰竭压力下原油的真实体积系数和溶解气油比。
将多次脱气实验初始饱和压力状态作为第 0级,设最终标准状况下残余油体积为1 m3,则钢瓶中油相体积Vodb数值上等于多次脱气实验测定的饱和压力下原油体积系数,饱和压力下真实原油体积系数等于单次脱气实验测定值Bob,那么饱和压力下液态油体积即为:

同理,在j级压力下钢瓶中的油相体积Vod,j数值上等于多次脱气实验测定的原油体积系数,设该级压力对应原油的真实体积系数为Bo,j,那么剩余液态油体积即为:

多次脱气实验第j级压力下放出的气量Vsd,j-1-Vsd,j,数值上等于第(j-1)级与j级测定的溶解气油比之差,相应压力下等容衰竭实验测定的凝析油含量为Rv,j,则该级压力下放出的气态油体积为(Vsd,j-1-Vsd,j)×Rv,j。从第0级到第j级放出的气态油体积之和即为第j级压力下累计放出的气态油体积Vp,j:
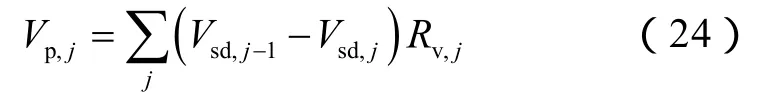
选取第j级放气结束时刻为研究节点,此刻,钢瓶中不存在气态气,即Vfg=0,且整个实验过程仅产出气态油,地面油相体积平衡式应为:剩余液态油体积等于饱和压力下液态油体积与累计放出气态油体积之差,即:

将(22)式—(24)式代入(25)式,得到原油真实体积系数Bo,j:

将(26)式中的Vod,j用Vsd,j替换,即为溶解气油比的矫正公式:
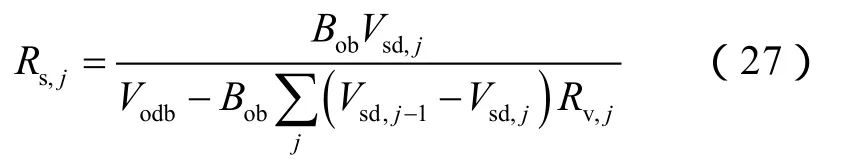
3 方法应用
基于表1中5个样品的实验数据,首先采用实验数据矫正方法,对多次脱气实验测定的原油体积系数和溶解气油比进行矫正,继而采用本文采收率预测改进方法进行等容衰竭实验模拟,以验证改进方法的可靠性;最后,分别采用“实验数据-传统方法”、“矫正数据-传统方法”、“矫正数据-改进方法”3种方法预测对比原油溶解气驱采收率,以明确脱出溶解气中凝析油含量对原油采收率的影响。
3.1 实验数据矫正
采用(26)式、(27)式对多次脱气实验数据进行矫正(见图 1、图 2),从图中可以看出典型黑油(样品5)矫正前后的原油体积系数、溶解气油比曲线基本重合,中—弱挥发性原油(样品3、样品4)矫正前后数据曲线出现明显差异,强挥发性原油(样品1、样品2)的数据差异进一步加大。对比实验数据可知,不同油样矫正前后的差异取决于溶解气油比以及溶解气中的凝析油含量,溶解气油比高、原油体积系数高的强挥发性原油经过数据矫正后收缩性大幅度降低。
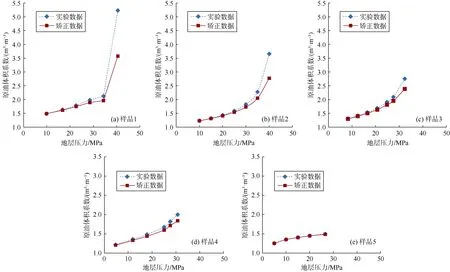
图1 多次脱气实验测定的原油体积系数矫正结果
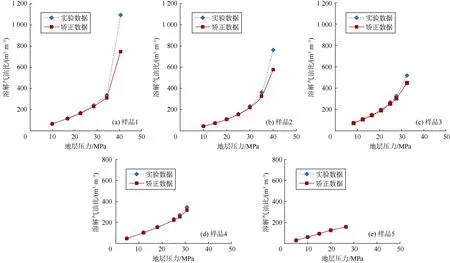
图2 多次脱气实验测定的溶解气油比矫正结果
3.2 实验模拟与方法验证
挥发性原油 PVT等容衰竭实验过程保持容积不变,只采出自由气,因此,将Kro=0,Swi=0代入本文改进方法基本方程(16)式、(18)式和(21)式,即可模拟PVT等容衰竭实验过程。实验流体基本参数中,原油体积系数和溶解气油比为多次脱气实验矫正后数据,计算截止的废弃压力取原始地层压力的1/4。
图3a为5个样品通过本文改进方法计算的原油饱和度与实验测定值对比,每个样品的模拟结果和实验数据均吻合较好,说明本文计算方法可靠;图3b为5个样品等容衰竭实验条件下计算的原油采收率,由此可见,尽管假定自由油相不流动(Kro=0),但计算的强挥发性原油(样品 1、样品 2)最终采收率分别达20.28%、15.35%,说明挥发性油藏脱出溶解气中的凝析油对产油量有重要贡献。

图3 等容衰竭实验中改进方法的模拟预测结果
另外,从与已有方法的继承性上也可以验证新方法的可靠性。若将凝析油含量Rv=0代入改进方法基本方程(16)式、(18)式、(21)式,可得到与传统方法基本方程(2)式、(3)式、(5)式完全相同的形式,说明本文改进方法是对传统方法的继承和发展。
3.3 不同方法计算的原油采收率对比
对每一种原油分别采用3种方法计算,方法1:直接基于多次脱气实验数据,采用传统溶解气驱油理论预测采收率,简称“实验数据-传统方法”;方法2:基于矫正后的实验数据,采用传统溶解气驱油理论预测采收率,简称“矫正数据-传统方法”;方法3:基于矫正后的实验数据,采用本文提出的改进方法预测采收率,简称“矫正数据-改进方法”。所有算例都采用相同油气相对渗透率曲线(见图4),束缚水饱和度为30%,计算截止的废弃压力都取原始地层压力的1/4。

图4 油气相对渗透率曲线
图5为3种方法计算得到的原油采收率与地层压力关系曲线,由此看出对于典型黑油(见图 5e)3种方法计算结果差异不大,“实验数据-传统方法”、“矫正数据-传统方法”、“矫正数据-改进方法”预测最终采收率分别为12.34%、12.52%、12.74%;中—弱挥发性原油的3种方法计算结果出现明显差异,基于样品4预测的原油最终采收率分别为16.21%、17.57%、19.74%(见图 5d);基于样品 3预测的最终采收率分别为17.37%、19.33%、23.29%(见图 5c);强挥发性原油的3种方法计算结果差异进一步增大,基于样品2预测的最终采收率分别为20.82%、24.16%、30.45%(见图5b);基于样品1预测的最终采收率分别为24.76%、28.26%、35.93%(见图 5a)。说明对于典型黑油,采用“实验数据-传统方法”计算可以得到与改进方法计算近似的结果;对挥发性原油,不仅需要对实验数据进行矫正,还需要采用改进的新方法计算。
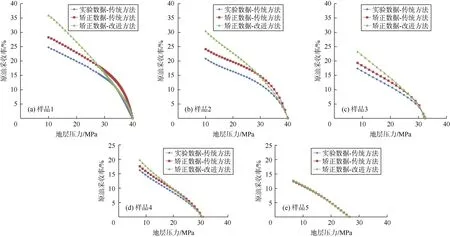
图5 3种方法预测的原油采收率对比
以“矫正数据-改进方法”计算的原油采收率为基准,统计“实验数据-传统方法”、“矫正数据-传统方法”计算的原油采收率相对误差的绝对值,发现其与原始溶解气油比存在较好的相关性(见图 6)。在总相对误差为10%时(其中实验数据造成的相对误差为3.8%;计算方法造成的相对误差为6.2%),对应原始溶解气油比约为235 m3/m3,若原始溶解气油比大于235 m3/m3,推荐使用“矫正数据-改进方法”;若原始溶解气油比小于 235 m3/m3,“实验数据-传统方法”或“矫正数据-传统方法”均不会造成较大误差(小于10%)。因流体物性影响因素复杂,包括组成、压力和温度,单一指标很难界定,只要资料条件允许,无论原油挥发性强弱,采用“矫正数据-改进方法”计算为宜。
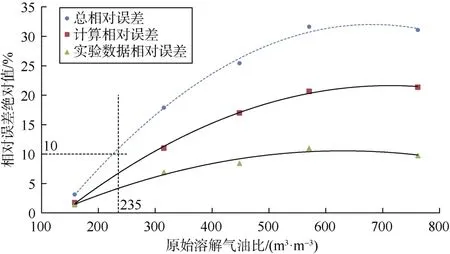
图6 计算误差分析图
结合挥发性油藏多次脱气实验和衰竭开发过程,分析不同方法计算结果的差异。无论是实验室条件还是油藏条件,在地层压力降低到饱和压力时,原油开始脱气,这是一个液态气逐步转变为气态气,并伴随液态油转化为气态油的过程,溶解气油比越高、凝析油含量越高,原始液态油转化为气态油的比率(当前压力下气态油体积与原始液态油体积之比)也就越高。在多次脱气实验条件下,气态油伴随自由气排出,并不包含在最终回收的油量中,而在油藏条件下,这些气态油可以通过 2个途径采出:一部分伴随自由气产出,一部分随压力下降再次转化为液态油,伴随自由油产出;最后,产出的气态油全部被地面设备回收。“实验数据-传统方法”从实验过程到开发过程都忽略了气态油的存在;“矫正数据-传统方法”虽考虑到实验过程气态油的影响,但忽略了开发过程中气态油的存在;“矫正数据-改进方法”则同时考虑了两个过程中气态油对原油采收率的影响。
从不同方法的计算结果对比可以看出,衰竭式开发的挥发性油藏也可以达到相当高的原油采收率。传统观念认为挥发性原油具有强收缩性将导致原油采收率较低,是基于多次脱气实验结果及传统溶解气驱油理论得出的,而本文研究发现,经矫正后的实验结果显示原油整体收缩性明显变弱,开发过程中脱出溶解气中凝析油对原油产量有着重要贡献。
4 结论
多次脱气实验测定的是脱出溶解气中的凝析油完全损失情况下的原油物性,测定条件与“生产过程中从油藏到地面设备没有流体外泄”的事实相悖,原油挥发性越强,凝析油损失越大,因此多次脱气实验原理导致挥发性油藏原油采收率被低估;传统方法实质上认为脱出的溶解气为干气,即原油产量始终且完全来自油藏油相,实际原油产量来自油、气两相,且随原油挥发性增强,气态油产量贡献也增大,因此传统方法预测的挥发性油藏原油采收率偏小。
随原油挥发性增强,“实验数据-传统方法”或“矫正数据-传统方法”适用性变差,仅适用于典型黑油和弱挥发性油(原始溶解气油比小于等于 235 m3/m3),而“矫正数据-改进方法”同时考虑到实验过程和开发过程气态油的影响,不受原油挥发性强弱的限制。本项研究证明了挥发油的强收缩性导致更多的液态油转化为气态油采出,衰竭式开发的挥发性油藏也可以达到相当高的原油采收率。
符号注释:
Bg——天然气体积系数,无因次;Bo——目前原油体积系数,无因次;Bob——单次脱气饱和压力下原油体积系数,无因次;Boi——原始原油体积系数,无因次;Bo,j——第j级压力下原油真实体积系数,无因次;Eo——原始原油膨胀系数,m3/m3;F——累计产出烃地下体积,m3;j——多次脱气压力级;Krg——气相相对渗透率,无因次;Kro——油相相对渗透率,无因次;qfg——瞬时气态气产量,m3/d;qfo——瞬时液态油产量,m3/d;qg——瞬时总产气量,m3/d;qo——瞬时总产油量,m3/d;Rgo——传统方法计算的瞬时生产气油比,m3/m3;Rgo*——改进方法计算的瞬时生产气油比,m3/m3;Ro——传统方法计算的原油采收率,%;Ro*——改进方法计算的原油采收率,%;Rps——传统方法计算的累计生产气油比,m3/m3;Rps*——改进方法计算的累计生产气油比,m3/m3;Rs——原油溶解气油比,m3/m3;Rsi——原始原油溶解气油比,m3/m3;Rs,j——第j级压力下原油真实溶解气油比,m3/m3;Rv——凝析油含量,m3/m3;Rv,j——第j级压力下放出气中凝析油含量,m3/m3;So——传统方法计算的原油饱和度,%;So*——改进方法计算的原油饱和度,%;Swi——原始含水饱和度,%;V——原始原油储量,m3;Vfg——剩余气态气体积,m3;Vfo——剩余液态油体积,m3;Vfoi——原始液态油体积,m3;Vfo,j——多次脱气第j级压力下液态油体积,m3;Vodb——多次脱气饱和压力下钢瓶中油相体积,数值上等于多次脱气实验测定的饱和压力下原油体积系数,m3;Vod,j——多次脱气第j级压力下钢瓶中油相体积,数值上等于多次脱气实验测定的原油体积系数,m3;Vp——累计产油量,m3;Vp,j——多次脱气第j级压力下累计放出的气态油体积,m3;Vsd,j——多次脱气第j级以下压力级放出的总气量,数值上等于第j级压力下测定的溶解气油比,m3;Vsd,j-1——多次脱气第j-1级以下压力级放出的总气量,数值上等于第(j-1)级压力下测定的溶解气油比,m3;μg——地下气相黏度,mPa·s;μo——地下油相黏度,mPa·s。

