半导体制冷箱温度场分析

王成刚 韩 崇 郭佳欢

（武汉工程大学 机电工程学院）

0 引言

随着科技技术不断发展，人类对生态环境的要求也逐渐提高，无污染的制冷方式越来越受到重视，半导体制冷方式具有无需使用压缩机、制冷剂，制冷响应快，结构简单和无噪音等优点，被广泛应用于电子冷却。军事装备、医疗卫生、智能生活、航空航天及科研等领域[1-3]。制冷速率和温度均匀程度是评价制冷箱性能的重要指标，大量学者对散热器结构及热端散热方式对半导体制冷模块的最佳制冷效果的影响进行了研究。本文以整个箱体为研究对象，通过ANSYS软件，针对某半导体制冷箱基于有限元体积法对箱体进行了仿真分析，对比制冷箱不同工况的温度分布情况，研究了冷端对流方式及制冷片分布位置对于制冷空间制冷效果的影响。

1 半导体制冷器工作原理

半导体材料具有一种重要特性，当在其中掺入一定量的杂质后，能够极大地改善半导体材料的导电能力[5-7]。且掺入不同的杂质能够使半导体材料呈现不同的特性。根据掺入杂质后半导体材料载流子是放出自由电子还是形成“空穴”，能够把半导体材料分为N 型半导体和 P 型半导体。一个由 P 型半导体材料形成的电偶臂与一个由 N 型半导体材料形成的电偶臂通过金属电桥连接在一起，就构成了一个热电偶——即半导体制冷器的基本结构单元。当有直流电通过热电偶内部时，在外加电场的作用下， N 型半导体中的自由电子和 P 型半导体中的空穴会按照一定的方向开始运动，而载流子在金属内的势能低于半导体，当空穴沿电流方向从金属电桥进入P 型半导体时，热电偶冷端需要吸收热量；而当空穴流经 P 型半导体离开进入金属片时，热电偶热端需要释放热量。同样，当电子沿电流相反方向从金属电桥进入 N 型半导体时，热电偶冷端需要吸收热量；而当电子流经 N 型半导体进入金属片时，热电偶热端需要释放热量，从而实现能量转换与热量传递过程。当众多热电偶依次串联在一起，就构成了半导体制冷器，其结构如图1所示[8]。

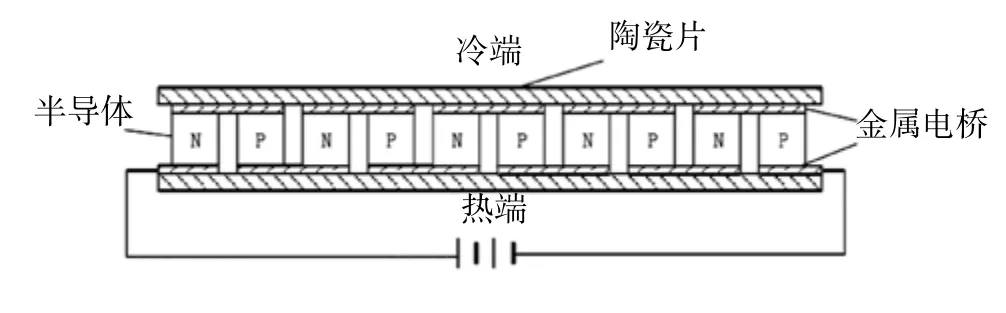
图1 半导体制冷器示意图

2 半导体制冷箱模型

2.1 物理模型

半导体制冷箱由保温层、箱体内胆、半导体制冷片、冷端散热器等部分组成，导入ANSYS软件的半导体制冷箱的几何模型如图2所示，制冷箱外部保温层尺寸为264 mm×264 mm×264 mm，保温层选用厚度为30 mm的聚氨酯材料，内胆选用厚度为2 mm的铝板组成，尺寸为204 mm×204 mm，制冷箱内部空间尺寸为200 mm×200 mm×200 mm，单个半导体制冷片尺寸为40 mm×40 mm×3.8 mm，模型共分为5个实体部分，将内部空气部分设置为流体区域，其他部分设置为固体，建立的半导体冷箱的几何模型如图2所示，计算过程使用直角坐标系求解。

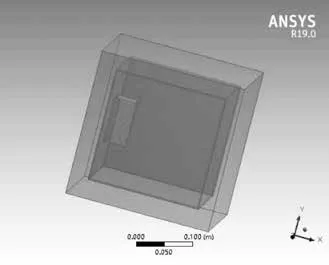
图2 半导体制冷箱几何模型

2.2 数学模型

箱体内的传热是一个热传导、热对流和热辐射相互耦合的非稳态过程，且箱体和系统之间存在耦合作用。简化计算模型后，对冷箱内空气的换热及流动进行如下假设：将冷箱内空气视为不可压缩理想气体；冷箱内空气与冷端接触面保持无滑移边界条件；不考虑冷箱开口热量泄漏；制冷过程中箱内热量传递为热传导和热对流，忽略热辐射影响；考虑箱体内空气重力的影响，Y方向重力加速度大小为-9.8 m/s2。

2.3 控制方程

制冷箱工作时，系统从一个稳定状态向新的稳定状态过渡，这个过渡过程为非稳态的传热过程，控制方程为：

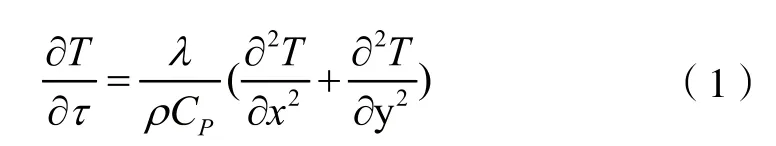
当在系统运行一段时间，温度不再发生较大的波动时，此时为稳态传热过程，控制方程为：

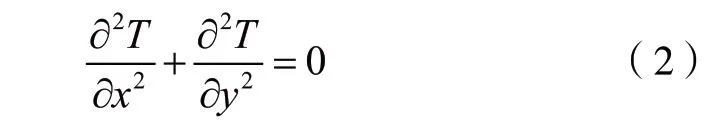
2.4 初始条件及边界条件

在系统刚刚开始运行的时刻,制冷箱各部件之间还未发生热交换，温度场基本处于均匀状态，此时可以认为，制冷箱内温度与室内温度相同，即＝0，T＝T0。

传热过程中的边界条件分为三类：第一类边界条件是指物体边界上的温度函数为已知；第二类边界条件是指物体边界上的热流密度为已知；第三类边界条件是指与物体接触的流体介质的温度和换热系数为已知。本文仿真过程中涉及空气对流换热及气体和固体耦合换热过程，将半导体制冷系统边界条件设置成第三类边界条件。

2.5 网格划分及物性参数

将流体区域及固体区域均设置为四面体网格，生成的网格相关信息及箱体材料如表1及表2所示。

表1 网格相关信息

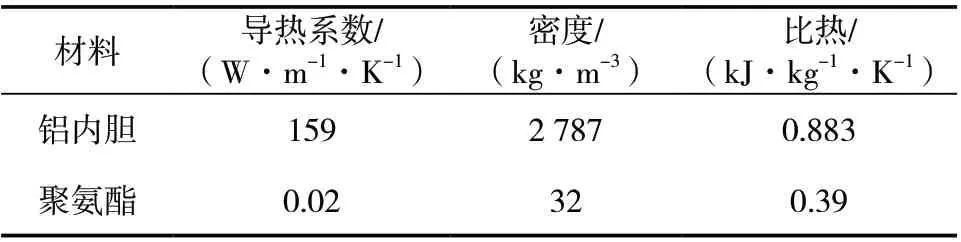
表2 箱体物性材料参数

3 仿真结果及分析

整个仿真过程可分为两大部分：

（1）除冷端对流方式不同以外，其他条件设置相同，通过冷端自然对流和冷端强制对流的温度云图的对比，分析对流方式对制冷效果的影响。

（2）对六种不同方式的冷端安装位置进行仿真分析，获得不同方案制冷空间的温度分布云图，通过监测冷箱内部中心点的温度变化情况，确定最优的制冷排列位置。

3.1 冷端自然对流与强制对流时制冷箱内温度分布影响

强制对流的空气对流系数大于自然对流系数，为了验证自然对流与强制对流的影响，设置环境温度为303 K，仿真时间为600 s，在冷端排布相同时，改变冷端对流换热系数，进行仿真分析。计算完成后，从冷端中间上下剖开分析上下面的温度场分布情况来分析整个制冷箱内部的温度场，结果如图3所示。

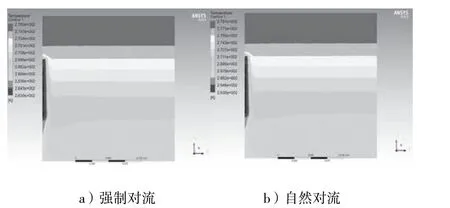
图3 强制对流和自然对流温度云图

从图3可知，仿真分析结束后，冷端采取自然对流时箱内最高温度为279.1 K，而冷端采取强制对流时箱内最高温度为274.1 K，在相同设置下冷端采取强制对流的方式制冷箱内最高温度比冷端采取自然对流时要低5 K左右，说明了空气对流系数增大会加强制冷空间的空气流动，大大增强制冷效果，减小制冷空间的温度梯度。

3.2 制冷片安装位位置对制冷箱内温度分布影响

为了验证制冷片不同安装位置对制冷箱内温度分布的影响，设计了六种冷端排布方式，如表3所示，并对不同方案进行了模拟分析。

表3 六种排列方式冷端位置分布表

将六种不同的排列方式分别进行600 s的仿真分析后，得到对应的制冷箱内温度场分布图，具体如图4所示。

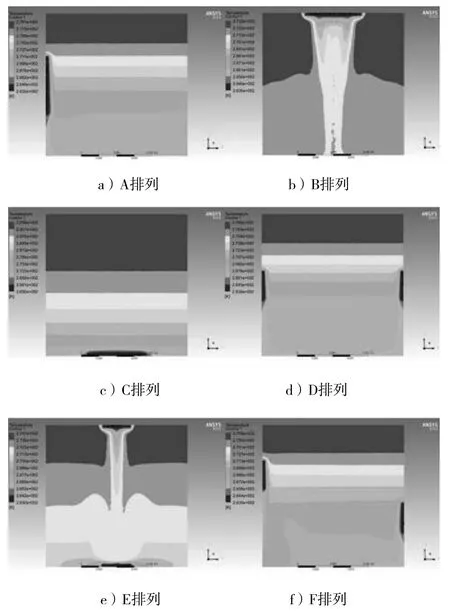
图4 六种排列方式的温度云图

由图4可知，6种排列方式在系统稳定时制冷空间内温度最大值分别为279.1 K、273 K、293.8 K、278.5 K、274.7 K、276 K。6种方案的制冷空间温度分布呈现自上而下的分层，最高温度均出现在上半区和距离冷端较远的位置。冷端位置采用B排布方式时，制冷箱内有一半区域温度维持在270 K，此外没有出现均匀的温度分层现象，在六种排列方式当中效果最佳。冷端位置按照C排布方式时，制冷箱内有1/3的区域温度为293.8 K，箱内上下温差达到了30 K，是六种方案当中温差最大的。主要原因是冷端排布在底部，冷空气下沉，箱体上方空间的空气不能及时冷却。

由以上分析可以看出，冷端的排布位置对制冷空间内的温度分布有很大的影响。随着冷端位置升高，制冷空间内部的空气温差逐渐减小，温度梯度也减小，空间内温度越均匀，越有利于半导体制冷箱性能的优化。

为了确定冷端采取哪种排列方式冷箱内降温更迅速，每60 s对冷箱中心点温度进行一次采集，6种排布方式中心点的温度变化情况如图5所示。

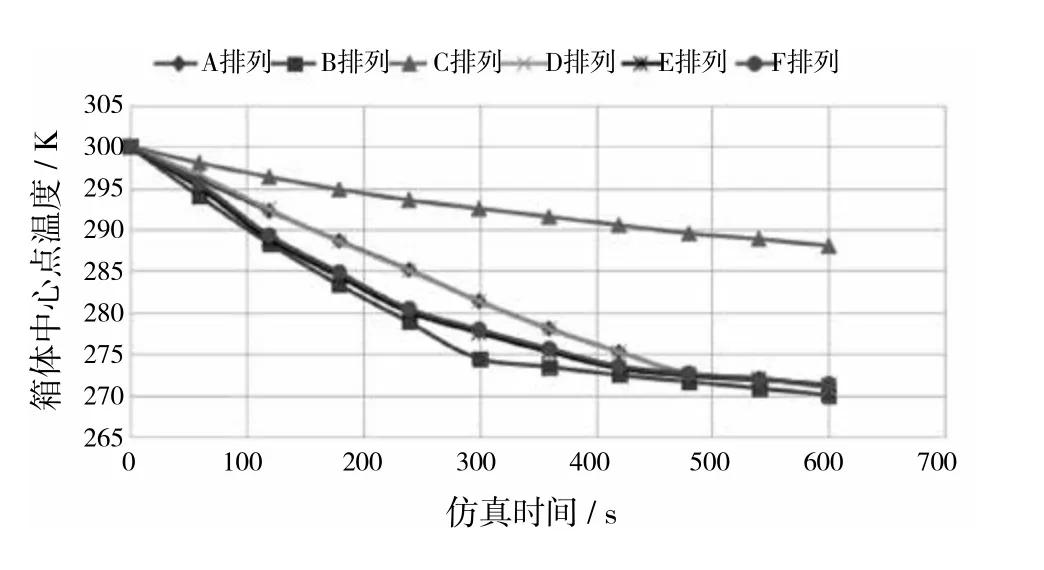
图5 六种排列方式冷箱中心位置温度时间履历图

由图5可知，制冷系统运行结束时，C排列方式中心点温度最高，其他五种排列方式中心温度都约为（272±2）K。在六种排列方式中，B排列方式冷箱中心点温度下降速率最快，能够更快达到预期温度。同时冷箱内中心温度最低，箱内温度差值也最小，温度分布最均匀。

4 结论

（1）制冷箱冷端采取强制对流的方式时，其制冷速率大于自然对流，同时制冷箱内空气温差值更小。

（2）通过对比6种排列方式可知，冷端位置的排布对制冷空间温度分布有很大影响。当两片制冷片安装在制冷箱顶部时，制冷箱内温差最小，温度分布最均匀。

（3）设计冷箱时可采用顶部安装制冷片并在冷端采取强制对流的散热方式，这种设计方案制冷空间降温迅速且温度分布较为均匀。