基于虚拟电厂的多元小微主体参与现货市场的竞价策略

宋大为，尹硕，何洋，李志恒，张钧钊，姜欣

(1. 国网河南省电力公司经济技术研究院，郑州450052；2. 国网河南省交易中心有限公司，郑州450056；3. 郑州大学电气 工程学院，郑州450001)

0 引言

多元小微主体是指功率不大、建设在负荷中心附近的、模块式采用先进信息控制技术的、清洁环保、经济、高效、可靠的自主智能供电形式[1]。其种类繁多，包括分布式电源(风电、光电)、储能装置以及需求侧响应等。多元小微主体在电力需求侧作为电力供应侧的有力补充，在优化调整负荷曲线、调节电力价格、降低能量传输损耗、缓解电力系统阻塞、提升电力系统清洁性等方面具有重要作用。然而，多元小微主体中的分布式发电(distributed generation，DG)给电力系统的运行带来了许多挑战，其有限预测性和高可变性使得DG无法被直接调度[2 - 5]。需求侧响应(demand respond，DR)和分布式储能(distributed storage，DS)已经被证明是部署智能电网最重要的关键因素，可有效缓解高比例DG渗透带来的挑战并提高系统可靠性[6 - 9]。虚拟电厂(virtual power plant，VPP)被认为是实现DG与DR和DS成功耦合的有效途径[10 - 13]。

随着我国售电市场不断放开，VPP作为一种特殊形式的售电商，其参与现货市场最优竞价问题亟待研究。尽管文献中有丰富的处理传统电厂日前(day-ahead, DA)竞价策略问题的优化模型但目前针对VPP的相同问题的研究还很少[14 - 15]。文献[16]考虑了由可中断负荷、储能、可调度发电厂组成的VPP，提出了两阶段随机混合整数线性规划(mixed integer linear programming, MILP)竞价模型，模型同时考虑了日前能量市场与平衡市场，在第一阶段模型中VPP被视为价格接受者，在第二阶段模型中VPP被视为偏离者(即被动代理人)。文献[17]提出了一个VPP参与日前市场的最优竞价策略问题，在一个混合整数非线性规划框架下，使用概率性的投标报价法和点估计法对市场价格和发电资源的不确定性进行建模。文献[18]给出了由风电场、光伏电厂和燃气电厂组成的VPP的最优投标策略问题。该问题被表述为MILP模型，并将长期双边合同与VPP在DA市场的参与结合起来。文献[19]建立了传统发电商、售电商与VPP同时参与市场竞争的分段报价模型和优化出清模型，采用分段线性的方法得到了VPP在不同时段采取的不同报价策略。文献[20]建立了VPP的电价竞标模型和电量竞标模型，将Stackelberg博弈理论应用于VPP的电价竞标和电量竞标过程中，确定VPP内多个分布式电源与控制协调中心的交易电价与调度计划。文献[21] 为减小可再生能源发电的波动性和间歇性对电网造成的冲击, 提高电网运行的经济性, 提出了一种考虑VPP和分时电价的风光火储系统两阶段优化调度策略。通过对以上VPP参与现货市场的竞争策略的分析，可以发现以下两点不足。

1)大部分文献在VPP参与现货市场的竞价中，都把VPP看作是电力市场价格的接受者，即它没有能力为了自己的利益改变市场结算价格。但是随着售电侧改革不断推进、分布式能源大量并网和互联网技术的不断发展，售电将直接面向终端用户。此时用户的出力变化和策略优化调整将会对市场价格产生影响，因此再把VPP看作是电力市场价格的接受者是不满足要求的。

2)鲜有文献研究VPP参与现货联合市场的竞价策略，以及竞价决策过程中自身报价的随机性和竞争对手策略的不确定性对竞价策略的影响。

因此，本文从多元小微主体参与现货市场出发，提出了一种基于VPP的两阶段双层联合竞价模型。首先第一阶段，依据先进的信息通信技术和控制架构，把多元小微主体聚合成一个VPP。其次根据对多元小微主体的出力特性分析，对整个VPP内部进行优化调度，由此确定整个VPP充放电的上下限。第二阶段为VPP参与日前能量市场与辅助服务市场联合竞价策略主从博弈模型，其目标为与预期的实时生产和不平衡费用最小化相结合的日前利润最大化。引入多场景描述交易决策博弈过程中竞争对手的不确定性给VPP收益带来的风险，保障VPP理性参与市场化交易。

1 多元小微主体的聚合模型

1.1 多元小微主体聚合模型

多元小微主体接入电网是对电力系统发电侧一次巨大的补充。由于多元小微主体具有快速调频以及快速响应能力，使得电网更加稳定、可靠地运行。但鉴于多元小微主体容量、体积较小的缘故，其很难直接被电网调度和管理。为了更好地管理多元小微主体，使其在电网运行中发挥有益作用，多种聚合技术营运而生，这些技术以高级计量设备、智能电网设备、先进通信系统为基础，作为电网与多元小微主体的中间层存在于电力系统中。而其中应用最广泛的一种技术当属虚拟电厂技术。VPP将各类分布式资源有机结合，并利用相关调控、通信技术实现整体管理(如图1所示)。

把各个多元小微主体聚合为一个VPP后，整个VPP对外表现的模型就是售电与购电的过程，其模型可以表示为：

(1)

1.2 多元小微主体不确定性分析

把各多元小微主体聚合成一个VPP后，首先要预测风电与光伏的出力曲线，再对VPP内部进行优化调度，大致确定第二天VPP的出力曲线，从而更好地制定VPP参与日前能量市场与辅助服务市场的竞价策略。本文首先利用拉丁超立方抽样法生成风电机组与光伏机组出力的场景集，再基于后向场景缩减技术生成3种经典场景[22]，最后采用概率加权法计算平均出力曲线，即最优预测曲线。

2 基于主从博弈的VPP竞标模型

2.1 Stackelberg博弈

Stackelberg博弈模型适用于有主从递阶结构的动态博弈关系，参与者通常被分为两种：领导者和跟随者。领导者首先做出决策，跟随者可以观察到领导者的决策，从而做出自己的决策。VPP首先要考虑的自身利益最大化，但是也要考虑到其他竞争对手报价和网络运行约束来进行报量报价。调度和交易中心得到市场各主体的报量报价后依照系统购电成本最小为目标进行日前能量市场和辅助服务市场的统一出清，得到日前能量市场和辅助服务市场各时段机组的出清电量和出清电价。因此，VPP参与现货市场竞价的博弈过程可视为一种Stackelberg主从博弈，其中VPP为决策的领导者，调度和交易中心为决策的跟随者。

虚拟电厂作为Stackelberg博弈中的上层领导者，其参与竞价的目标函数为：

(2)

调度和交易中心作为Stackelberg博弈中的下层领导者即跟随者，其目标是以系统总报价成本最小为目标函数，其表达式为：

(3)

2.2 基于Stackelberg博弈的VPP模型架构

如图2所示，第一阶段以VPP优化调度为研究对象，目的是确定VPP出力的上下限，受到各多元主体运营约束以及VPP内部功率平衡约束。第二阶段为Stackelberg博弈双层模型，上层模型以VPP作为研究对象，建立VPP作为投标主体进行竞价决策的交易决策模型；下层模型为现货市场出清模型，包括集中竞价交易模式下日前电能量市场与辅助服务市场联合出清。上层模型中的VPP作为领导者以自身利润最大化为目标函数进行日前联合竞价，并受到外部的竞标约束以及内部调频容量、调频里程的约束。下层模型是以调度和交易中心为跟随者，以购电成本最小为目标函数，并受到日前功率平衡约束、网络安全约束等约束。

图2 VPP参与现货市场竞价的博弈模型架构Fig.2 Game model architecture of virtual power plant participating in joint market bidding

3 VPP参与现货联合市场竞价模型

3.1 VPP协调优化调度模型

3.1.1 目标函数

将多元小微主体聚合为一个VPP，根据风电、光伏的预测曲线，调节储能装置各时段充放电功率、负荷削减量和VPP与上级电网购售电量，以VPP运行成本最小为目标，协调调度内部各小微主体。并将优化后的出力曲线作为下阶段系统运营优化的基础，其目标函数为：

(4)

3.1.2 约束条件

1)VPP内部功率平衡约束

(5)

2)风电

(6)

3)光伏

(7)

4)分布式储能

(8)

5)可调负荷

(9)

3.2 上层交易决策模型

3.2.1 目标函数

VPP参与现货零售市场的收益包括日前能量和日前调频市场的总收益，其目标是日前能量与日前调频市场相结合的日前利润的最大化，VPP在参与日前能量与辅助服务市场报价时，需同时考虑不同场景下日前市场价格期望曲线，每一个竞争对手的报价策略为价格期望曲线上或者曲线上方或下方的一个点且都会影响日前市场价格期望曲线的趋势，而大体量的竞争对手的报价在日前市场更具有话语权，更能够影响价格期望曲线的趋势。因此本文选取不同场景下典型竞争对手的报价，根据其典型竞争对手的报价及时调整自己的报价策略，使自身的收益最大化。为了精准地预测典型竞争对手的报价，本文首先通过拉丁超立方抽样生成典型竞争对手报价场景集，再基于场景缩减技术选取典型竞争对手报价的典型场景r。其目标函数为：

(10)

值得说明的是：典型竞争对手的不确定报价报量信息将影响第二阶段下层联合市场的出清结果，下层出清得到的现货市场价格返回上层又将进一步影响VPP报价。因此，下层目标函数考虑期望场景时，上层VPP交易决策模型中的目标函数中也需要将不确定场景包含在表达式中。

3.2.2约束条件

1)VPP竞标电量约束

考虑到 VPP 与主网传输功率限制，VPP 在电力市场的竞标电量需满足如约束式(11)所示。

(11)

2)VPP上下调容量约束

(12)

3)VPP上下调里程约束

(13)

3.3 下层交易决策模型

3.3.1 日前能量市场联合出清模型

调度与电力交易中心为下层决策者，即Stackelberg博弈中的跟随者，根据市场中的需求状况、以及电力市场中其他典型竞争对手的报价策略、报价偏好和发电成本等，在满足供需平衡以及各类机组安全约束的条件下，进行日前联合市场出清，其目的是使总购电成本最小。其目标函数为：

(14)

约束条件：

1)能量市场功率平衡约束

(15)

式中PL,t为t时刻系统负荷的大小。

2)网络安全约束

pl,min≤pl,t≤pl,max

(16)

式中：pl,t为线路在t时刻的潮流；pl,max、pl,min分别为线路的最大、最小传输容量。

3)系统调频容量约束

(17)

4)系统调频里程约束

(18)

5)常规机组功率约束

(19)

式中：Pg,t,r为t时刻机组g的出力值；Pgmax、Pgmin分别为机组g的最大、最小出力。常规机组约束还包含爬坡约束、申报的调频容量和里程约束等其他约束。其中，申报的调频容量、里程约束与储能的形式相同。中标量约束包括常规机组各时段中标量之和不超额定容量以及储能各时段中标量之和不超额定容量和额定功率。在此都不作赘述。

3.4 模型求解

本文提出的VPP报价策略模型属于非线性、混合整数优化问题，模型的非线性来源于第二阶段上层模型中的双线性项：各交易类型中VPP的申报量和申报价格，因此重点阐述对第二阶段的求解过程，具体的步骤如图3所示。

图3 模型求解流程图Fig.3 Model solving flowchart

4 算例分析

4.1 基础数据

本文以风电机组、光伏机组、储能机组和4 000户家庭构成的VPP为算例，选取IEEE 30节点系统并进行适当的改进，其接线情况见附图A1。各机组参数及对应节点情况见附表A1。VPP内部优化调度后各主体充放电功率如图4所示。VPP内部优化后的负荷量如图5所示。系统上、下调频里程乘子分别见附表A2。机组调频市场报价情况见附表A3，并把聚合而成的VPP接入25节点。

图4 VPP内部优化后各主体充放电功率Fig.4 Charging and discharging power of each main body after internal optimization of VPP

图5 VPP内部优化过的负荷量Fig.5 Internal optimized load of VPP

4.2 各市场参与联合市场的竞价结果

4.2.1 各主体日前市场的中标量

市场各主体日前能量市场中标情况如图6所示。各市场主体日前辅助市场调频容量中标情况如图7所示。各市场主体日前辅助市场调频里程中标情况如图8所示。

由图6可以看出，在日前能量市场上，传统机组G1、G2提供了绝大多数能量，而VPP主要在1：00—6:00与13:00—15:00期间提供能量，这是由于风电在夜间提供了较大的出力，正午时太阳的光照能力较强，此时光伏提供较大的出力。在9：00—11：00与17：00—19：00期间VPP需要从电网购买电量，这是由于VPP内负荷用电量较大(见图4)。

图6 市场各主体日前能量市场中标情况Fig.6 Bid winners of the energy market in the energy market

图7 各市场主体日前辅助市场调频容量中标情况Fig.7 Bid winners situation of the auxiliary market frequency modulation capacity of each market entity

图8 各市场主体日前辅助市场调频里程中标情况Fig.8 Bid winners of the FM mileage of the auxiliary market in each market

对比图7和图8，VPP承担了系统主要的调频容量和调频里程任务。这是由于相较与常规机组的调节输出，提供相同的调节容量时，VPP中因含有分布式储能装置，在向上和向下方向上对调节信号的响应更加频繁，因此能够比常规机组提供更多的调频里程，在调频市场上会被系统优先调用。由图还可以看出G2机组在辅助服务市场中相对于其它常规机组，中标了大量的调频容量和调频里程，这是由于G2机组自身参数决定的，说明其对调节信号反应迅速，爬坡能力强。

不同市场主体在各市场的收益情况如表1所示。由表1可以看出，传统机组G1、G2、G6的主要收益主要来自日前能量市场，VPP的主要收益主要包括日前能量市场收益与调频容量收益。结果显示机组G4和G5在能量市场、调频市场上的中标量全为0(本文算例中选取的机组G4、G5发电成本和启停成本较高见附表A1)，表明G4和G5未参与到联合市场中运行，进而相应的市场收益(能量收益、调频容量收益、调频里程收益)合计为0。

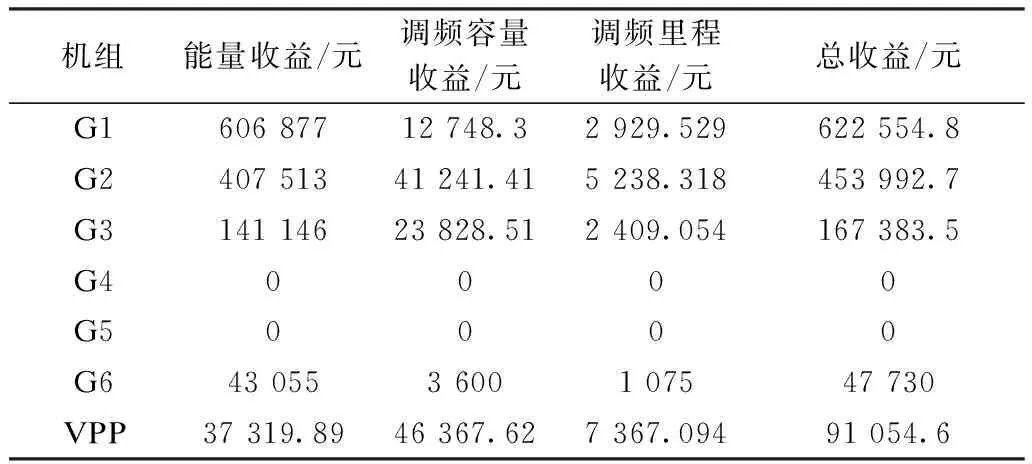
表1 不同市场主体收益对比表Tab.1 Comparison of income of different market entities

4.2.2 VPP的最优竞价策略

VPP在各市场中的最优报价如图9所示。VPP在各市场中的最优报量如图10所示。由图9可以看出，在不同的时段，VPP根据市场需求，上报不同的电价。而且由于VPP根据价格差来赚取利润，因此VPP放电报价总要高于充电报价。VPP调频容量报价虽然有所波动，但是整体维持在一条直线上，而VPP调频里程报价为一条直线。

图9 VPP在各市场中的最优报价Fig.9 The best quotation of VPP in each market

图10 VPP在各市场中的最优报量Fig.10 The optimal volume of VPP in each market

由图10可以更直观地看出，VPP在负荷较低的时段对其内部的储能装置进行充电，在负荷较高时，储能装置对外进行放电。VPP调频能力较高，所以其调频容量与调频里程的中标量较高。

4.2.3 联合市场的出清价格

日前能量市场联合出清价格如图11所示。日前辅助市场出清价格如图12所示。

图11 日前能量市场联合出清价格Fig.11 Day-ahead energy market joint clearing price

图12 日前辅助市场出清价格Fig.12 Day-ahead auxiliary market clearing price

图11可以看出，能量市场出清电价与负荷走势相近，呈现夜间低白天高的变化趋势，是由于常规机组按发电成本报价，报价和发电量线性相关，报价趋势和负荷走势相近。

由图12以看出，在日前辅助市场其调频容量以及调频里程的出清价格都是随着时间上下波动的。它们都遵循着一个规律：4：00—6：00出清的价格最低，12：00—14：00、20：00—23：00出清价格最高，但是整体的出清价格没有较大的波动，都维持在一个大致的水平上。

5 结论

本文基于Stackelberg主从博弈提出了一个VPP参与现货市场的两阶段随机双层优化竞价模型，用于优化由分布式能源资源、电池存储系统和电力用户组成的VPP组合参与现货市场的竞价策略，主要结论如下。

1)将多元分散的多元小微主体聚合为一个虚拟电厂VPP，由VPP运营商统一调度，可以很好地利用小微主体出力的互补性，提升了各主体的经济效益。

2)VPP在日前能量市场与传统机组进行联合竞价的时候，传统机组利用其出力大，频率稳定的特性，竞标到了绝大多数的电量。VPP只有在夜间或正午风电、光伏出力较大时才有较少的中标电量。

3)VPP在日前辅助市场上竞标到了绝大多数调频容量以及调频里程，这是由于VPP内部的储能设备发挥作用的缘故。在调频市场上，低廉的价格和优越的调频性能使得VPP被系统优先调用，获得可观收益。