感知探究迁移 深度互动学习——《组合图形的面积》教学实录（二）

文|汪艳红

【教学内容】

北师大版五年级上册第88、89 页。

【教学过程】

一、展示回顾，明晰概念

1.复习面积计算公式。

师：同学们，我们学过哪些平面图形？

（根据学生的回答，教师在白板上依次出示长方形、正方形、平行四边形、三角形和梯形）

师：给这些平面图形统一取个名字叫基本图形。（板书：基本图形）这些基本图形的面积怎样求？

（学生以抢答的形式分别说出各个基本图形的面积计算公式）

2.揭示组合图形的概念。

（教师利用白板出示将长方形、正方形、平行四边形、三角形、梯形动态拼成的火箭）

师：这个图形像什么？

生：火箭。

师：在2020年6月23日9时43 分，长征三号运载火箭搭载北斗三号最后一颗全球组网卫星发射成功！使我国成为世界上继美国、俄罗斯之后第三个拥有自己卫星导航系统的国家，打破了国外卫星导航领域的垄断。请用热烈的掌声向我国的航天人表达最诚挚的敬意吧!（播放火箭发射新闻视频）

师：火箭是由哪些基本图形组合而成的？

师：像这样，由几个基本图形组合而成的图形，我们叫它组合图形。（板书：组合图形）

3.感受组合图形在生活中的应用。

师：同学们，今天我们来认识组合图形，在生活中，哪些地方你见过组合图形？

4.认识辅助线。

课件闪动房子侧面，将侧面留在屏幕上，其余隐去。

师：这个组合图形是由哪些基本图形组成的？怎么才能一眼就看出来？

生：在上面画一条线，就可以很清楚地看出这个组合图形是由一个三角形和一个长方形组成的。

师：（根据学生的回答在图中添加一条辅助线）你的想法真不错，这条虚线叫做辅助线，它可是帮助我们分析思考的好伙伴。今天就借助辅助线来研究组合图形面积的计算方法。（板书：面积）

二、探索交流，寻求方法

1.估算引路。

（课件出示智慧老人家客厅的平面图）

师：同学们，智慧老人准备给客厅铺上地板，客厅地面是一个什么图形？

生：组合图形。

师：你们能根据图中的数据估一估智慧老人家客厅的面积大约有多大吗？

2.讨论思路。

师：同学们已经估算出客厅的面积大约是多少了，下面来验证智慧老人家的客厅面积究竟有多大。你们有什么好办法吗？

生：我觉得可以画一条辅助线把它分成两个基本图形，分别求出面积再相加。

生：我觉得可以画辅助线给这个组合图形补上一块，把它变成一个长方形，然后再把补上的面积减去。

师：这两个同学说得很有道理，通过添加辅助线，可以把组合图形转化成学过的图形。下面请小组合作，共同探索求这个组合图形面积的方法，看哪个小组想出的方法多。

3.合作探究。

学生先独立思考，然后小组合作。

（教师巡视，了解情况，指导帮助个别学生，提醒学生及时把想出来的方法记录在《学习单》上）

4.分享方法。

师：同学们，你们小组合作完成了吗？找到了几种方法呀？

（教师选择有以下五种方法的小组上台，利用实物投影进行展示，每人汇报一种方法）

图3

图4

图5

生1：我是这样想的，我把这个组合图形分成了一个长方形和一个正方形，（如图1）长方形的长是6 米、宽是4 米，面积是24 平方米，正方形的边长是3 米，面积是9 平方米。

图1

师：老师打断你一下，你是怎样确定分出来的是个正方形的？

生1：我用7 米减4 米得到下面那条边是3 米，看出它是一个正方形。

师：好，请继续！

生1：然后用长方形的面积24 平方米加上正方形的面积9 平方米，这个组合图形的面积是33平方米。

生2：我是这样想的，把这两个长方形的面积加起来就是组合图形的面积。（如图2）上面长方形的长是4 米，宽是6－3＝3（米），它的面积是4×3＝12（平方米）；下面长方形的面积是7×3＝21（平方米）；12＋21＝33（平方米），就是这个组合图形的面积。

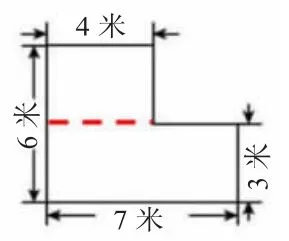
图2

师：这个同学很细心，用6－3＝3（米）求出上面长方形的宽。大家想一想不写这步可以吗？

生：不可以。

师：对，这是求这个组合图形面积要用到的条件，我们必须用缜密的计算步骤把它表示出来，缺少了可不行。

（依此类推，学生展示另外三种方法）

5.提炼方法。

师：观察以上五种方法，让你把它们分成两类，你打算怎么分？

生：把在图形里添加辅助线的归为一类，在外面添加辅助线的分为另一类。也就是把前三种分为一类，最后两种分为一类。

师：把组合图形分割成几个基本图形叫分割法。

师：同学们，老师有一个问题，你们在用分割法时都把组合图形分成了两个基本图形，为什么不分成三个、四个基本图形呢？

生：太麻烦啦！

小结：分割的方法越简洁，计算起来也就越简单。

师：把组合图形添补成一个大的基本图形叫添补法。

（板书：分割法、添补法）

6.拓展方法。

师：刚才我发现有位同学用了不一样的方法，请他说一说。

生：我把它先分成两个长方形，再把上面的长方形补到下面拼成一个长方形，求出长方形的面积是（7+4）×3=33（平方米），就是组合图形的面积。

师：我们又多了一种方法，但这样做得有条件支撑，上面长方形的宽是3 米才能补到这儿，这种先分割再添补的方法叫割补法。（板书：割补法）

小结：无论是分割、添补还是割补，目的都是将组合图形转化成已学过的基本图形。转化是我们学习数学的一种重要方法。（板书：组合图形基本图形）

师：在前面哪些知识的学习中用到了转化的思想？

生1：学习平行四边形面积、三角形面积、梯形面积时用到过，都是把这些图形转化成学过的图形来推导面积计算公式。

生2：在学习小数乘、除法时也是利用转化成整数乘、除法来学习的。

师：转化思想给我们的学习带来的帮助真是太大了，同学们要学会利用它。

7.估算评价。

师：同学们，我们之前在估算智慧老人家客厅面积的时候，就可以利用今天学到的方法来确定估算值的范围。比如：用分割法分成一个长方形和一个小正方形，大长方形的面积是24 平方米，那么我们就可以想到这个客厅的面积一定比24 平方米大；用添补法补成的长方形面积是42 平方米，我们就可以想到客厅的面积一定比42 平方米要小，其实刚才同学们估计的数值都在24～42 平方米这个正常值范围之间。总体上讲，大家估得都还不错。

三、练习巩固，拓展运用

1.基本练习。（教材第89 页练一练第1 题，略）

学生先估一估中队旗的面积大约有多大，再小组内交流不同的算法，然后选择合适的算法独立计算中队旗的面积，最后全班反馈。

2.变式练习。根据下面图形提供的数学信息，要求图形的面积，请选择正确的方法。

（学生作出选择后交流选择的理由）

小结：如果在分割和添补之后找不到相应的数据来计算这个组合图形的面积的话，那我们的分割和添补就是失败的。也就是说，我们在选择方法的同时，只考虑分割得简单可不行，还要考虑题目中所给的数据条件。

3.拓展练习。怎样计算涂色部分的面积？

四、总结回味，拓宽视野

师：通过本节课的学习，大家有哪些收获？

（播放课件）介绍我国古代数学家刘徽在《九章算术》中创建的割补术———出入相补原理。