冻土-构筑物界面粘聚-损伤-摩擦本构模型

陈 晓, 何鹏飞, 董建华, 任 新, 吴晓磊

(1. 甘肃建投土木工程建设集团有限责任公司, 甘肃 兰州 730050; 2. 兰州理工大学 理学院, 甘肃 兰州 730050; 3. 兰州理工大学 土木工程学院 甘肃 兰州 730050)

全年地表温度持续低于0 ℃或最冷季节低于0 ℃的地区称为冻土区,地球陆地面积约50%区域属于冻土区[1-2].我国是冻土分布大国,多年冻土和季节性冻土面积分别占国土陆地面积的21.5%和53.5%[1].随着经济社会的不断发展,在广阔的冻土地区修建了大量的交通、水利、能源、建筑工程.这些工程中不可避免地出现土体-构筑物接触面,在两者的相互作用体系中接触面的力学特征对构筑物的承载力和稳定性至关重要.在构筑物受荷时,接触面附近很薄的一层土体将出现强烈的非线性和大应变梯度变形.由于这层土体通常非常薄,方便起见在数学上通常会忽略其厚度,用界面模型来描述构筑物与土体之间的非线性变形.

界面本构模型是表征土体与构筑物发生相对位移过程中剪切应力-剪切位移关系的数学表达式.建立简洁、合理并能够方便数值分析的界面本构模型对模拟土体与构筑物界面相互作用有重要意义.目前关于融土与构筑物界面的本构模型研究较多,应用较多的有双曲线模型[3-4]、指数函数模型[5-6]、弹塑性模型[7]、幂函数模型[8]、损伤本构模型[9-10]、考虑接触面错动变形的刚塑性模型[11-12]、分形理论模型[13]和扰动状态理论模型[14]等.应用于冻土与构筑物界面的本构模型相对较少,董盛时等[15]使用双曲线模型对峰值强度前阶段的应力位移关系进行拟合,然后对饱和含水率下不同温度时的参数进行耦合,建立应力-位移-温度界面本构模型.杨平等[16]和Hu等[17]根据土体与结构面循环剪切试验结果，以不可逆体应变和可逆体应变的比值作为损伤因子,建立了除初始状态以外的任意状态接触面损伤本构模型.陈志良等[18]基于龚帕兹模型建立青藏冻结粉土-玻璃钢接触面剪切应力-位移本构模型.

这些本构模型在给定条件下都能得到较好的拟合效果,但它们都是基于界面的宏观变形特征提出的,忽略了界面细观破坏过程中胶结冰等提供的粘聚力的逐渐损伤过程及摩擦力的演化过程.冻土与构筑物界面的冻结力或摩擦阻力通常由两部分组成[19-22]：1) 冰与构筑物界面的粘结力；2) 土体与构筑物之间的摩擦力；对于粘性土还包括粘聚力.但已有的模型中忽略了界面胶结冰在剪切过程中对界面细观变形的影响,使预测的界面剪切过程失准.针对这一不足,学者们提出了粘结区域模型,并发展成为目前模拟界面结构中界面行为的一种常用方法[23-24].这一模型结合了界面细观变形过程中包括的界面粘结损伤、摩擦滑动和两者的耦合过程[25].其本构关系反映了界面变形的细观过程,包括了与界面变形过程相关的初始完整粘结作用，界面变形使得粘聚逐渐破坏、摩擦作用的演化和最终的界面滑动[26-27].模型中各参数的物理意义明确,数学表达式简单,能够方便地应用于数值分析中.本文将以上述理论为基础,考虑界面的细观变形过程,建立冻土-构筑物界面一维粘结-损伤-摩擦本构模型,并与已有试验数据进行对比验证其拟合效果.本文研究成果可为寒区工程中考虑界面特性的构筑物设计、分析和数值模拟提供参考.

1 冻土-构筑物界面剪切特性

通常,在界面含冰量较高时,冻土与构筑物界面的剪切应力(τ)与剪切位移(δ)关系表现为强应变软化型曲线[28],此时界面胶结冰的粘聚作用提供了较大的粘结力.在界面含冰量较低时,界面土体粘聚力相对胶结冰粘聚力很小,界面剪切行为表现为弱应变软化型.图1为典型的应变软化型曲线,根据曲线的特征可将其分为三个阶段：峰值前阶段、后峰值阶段和残余阶段.在峰值前阶段,剪切应力随着剪切位移的增大而快速增加,直到剪切应力的最大值，即峰值强度(τp),其对应的位移称为峰值位移(δp).在这一阶段,初始的线性变化阶段界面冰晶体保持完整状态,随后的非线性阶段界面冰晶颗粒开始逐渐破坏,并且颗粒(土颗粒、冰颗粒和冰包裹体)与构筑物表面的摩擦作用逐渐产生[29].在后峰值阶段,由于位移的增加，界面胶结冰大量快速的破裂,使得界面的胶结力明显下降，进而剪切应力出现快速下降[30].随后随着剪切位移的增加,剪切应力的变化逐渐放缓直至到达稳定值,这一阶段称为残余阶段.在残余阶段界面仍然具有一定的强度，称为残余强度(τr),其所对应的位移称为残余位移(δr).此时界面冰胶结力消失,剩余残余强度由摩擦力组成.上述界面的应力-位移变化过程表现出明显的粘结损伤和摩擦演化现象,同时摩擦作用在粘结损伤的初始阶段其实就已经开始发挥作用[31].

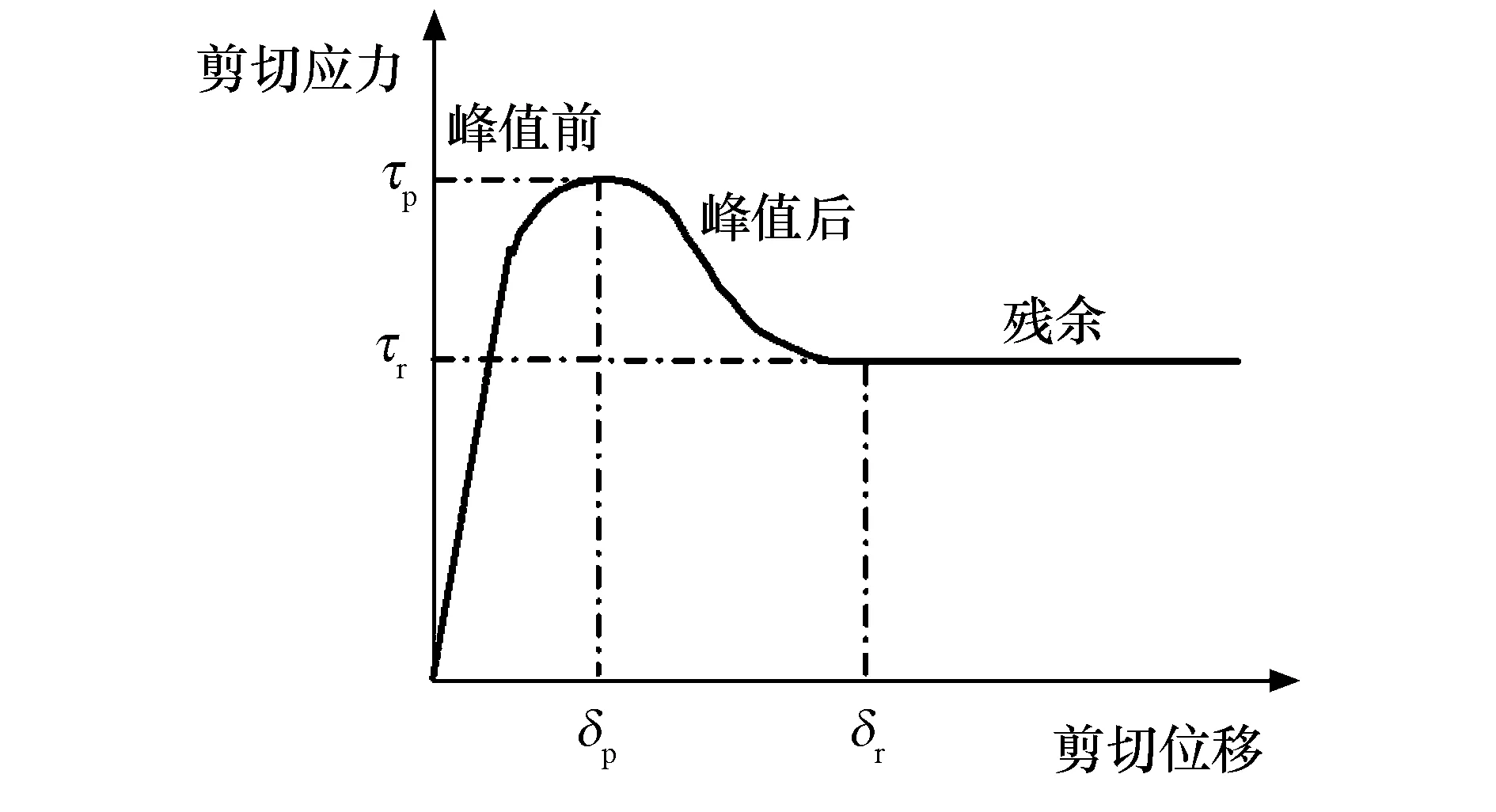
图1 典型冻土-构筑物界面剪切应力与剪切位移关系Fig.1 Typical relationship between shear stress and shear displacement of frozen soil-structure interface

2 基本概念

土体与构筑物界面的非线性剪切力学响应可通过粘聚-损伤-摩擦本构关系来描述.在细观尺度上,通过定义一个代表性的微元区域(REA)来区分区域内未损伤部分和完全损伤部分的相对关系,如图2所示.仅考虑一维的水平变形过程,假定界面为零厚度,忽略土体和结构的变形.图2所示微元区域的有限厚度只是为了让微元区域的描述更清晰.

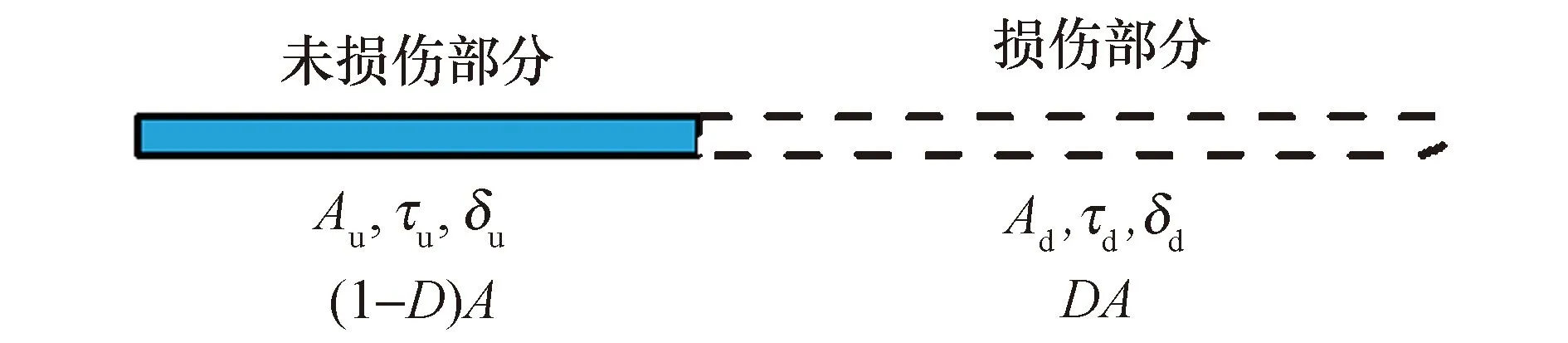
图2 界面微元区域Fig.2 Interface representative elementary area

与连续介质损伤力学模型中的相关定义类似[23],定义整个微元区域的面积为A,其中未损伤部分的面积为Au,界面处于完全粘结的状态.损伤部分的面积为Ad,界面开始出现相对运动.两部分对应的剪切应力分别定义为τu和τd,两部分的剪切位移分别为δu和δd.比例系数Ad/A称为界面损伤系数D，在未损伤时D为0,在完全损伤后为1,因此整个损伤演化过程可用D的变化来描述.

3 剪切应力-剪切位移关系

粘聚-损伤-摩擦模型是将考虑细观特征的模型粘聚力-水平位移关系和摩擦力-水平位移关系相结合得到的,如图3所示.图3a为粘聚力-水平位移关系(粘聚-损伤模型),可以看到它是一个双线性模型.在初始阶段随着位移的增加剪切应力线性增大,至剪切应力到达最大值τp,其对应的剪切位移为δp.随着剪切位移的发展,剪切应力开始线性降低直至0,其对应的剪切位移为δr.在粘聚-损伤模型中完整地反映了界面细观粘聚力的演化过程,从其开始发挥作用至最大值至最后完全破坏变为0.图3b为摩擦力-水平位移关系(摩擦模型).由于在界面变形的初始阶段,剪切带处于弹性阶段,界面没有摩擦力作用，因此在摩擦模型中摩擦的演化是从剪切位移为δp开始的,进一步随着界面相对位移的增加,界面的静摩擦力逐渐发挥作用.当剪切位移到达δr时,界面所有宏观连接的物质已经完全剪断,界面开始相对滑动,界面的静摩擦力转变为动摩擦力τf或残余应力τr,并且随着位移进一步地增加不再变化.界面所有连接物质完全剪断意味着粘聚作用的完全破坏.一般最大静摩擦力大于动摩擦力,这里为了分析假设两者相同.图3c为粘聚-损伤模型与摩擦模型的耦合模型,在此过程中,REA中损伤和未损伤部分面积的变化导致宏观剪切应力-剪切位移关系的非线性响应.

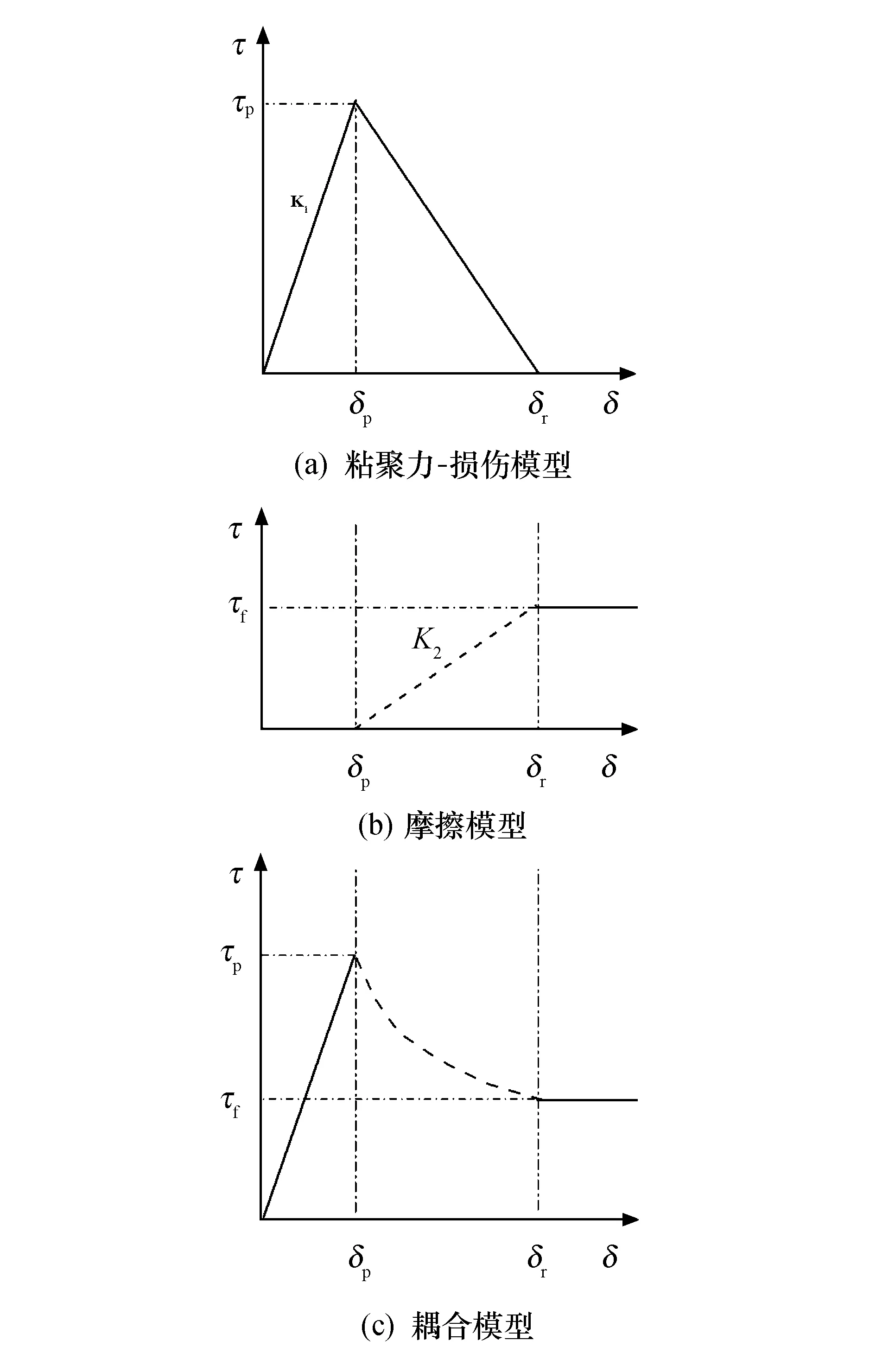
图3 界面的粘聚-损伤-摩擦模型Fig.3 Cohesion-damage-friction model of interface

界面耦合模型的基本运动学假设包括以下内容.

在整个微元区域上假设相对位移都是同步发生的,即：

δu=δd=δ

(1)

式中：δ表示界面的相对位移.

在微元区域内非损伤部分,界面的相对位移认为是完全弹性的.在损伤部分,界面相对位移可以分为两个阶段,即弹性位移阶段和非弹性位移阶段[23]：

δd=δde+δdi

(2)

式中：δde为弹性位移；δdi是非弹性位移.

从微观尺度上看,无论损伤部分还是非损伤部分,其各自区域内的应力都是非均匀的,但为了分析方便,假设各自区域内的应力是均匀分布的[23-24].如图3所示,在微元区域内非损伤部分的应力应变关系为线性关系：

τu=K1δu=K1δ

(3)

式中:K1是初始剪切刚度,可从试验数据中获得,也可通过K1=(cp+σNtan(φp))/δp计算得到.

在微元区域内的损伤部分,应力与弹性位移δde有关,界面的应力可表示为[23]：

τd=K2(δ-δdi)

(4)

式中:K2用以描述由于界面粗糙引起的弹性相互作用关系[23],K2与作用于界面的法向压力和界面摩擦角有关,可用下式表示：

(5)

损伤部分发生非弹性位移的判据通过下式确定：

τ-σNtan(φr)≤0

(6)

如果式(6)成立,则损伤部分发生的是弹性位移(δde),否则发生的是非弹性位移(δdi),并且界面的最大剪切应力为σNtan(φr).

式(4)至式(6)描述了微元区域内损伤部分的应力演化规律.为简化分析,可通过下式表示：

基于均匀化假设,采用加权法计算整个REA上界面应力的总值[23-24],

τ=(1-D)τu+Dτd

(8)

上式所描述的过程也就是在图3中所描述的过程.

4 损伤演化定律

从图3c中可以看出,在线弹性阶段(δ<δp),界面变形是弹性的,因此D=0.在δp<δ<δr的区域,界面开始逐渐损伤,同时摩擦作用开始演化,因此D逐渐增大.在δ>δp的区域,界面已经完全损伤,只有动摩擦力在作用,因此D=1.因此损伤变量D的演化过程可表示为[23],

(9)

最终,结合粘聚-损伤模型、摩擦模型、摩尔-库仑强度准则及损伤演化方程,得到界面剪切行为的本构关系为：

(10)

界面的损伤变量D反映了界面从开始完整状态到最终完全破坏状态,可表示为:

(11)

该模型通过对简单、易于建立的粘聚-损伤模型、摩擦模型和摩尔-库仑准则的耦合,提供了对界面剪切行为的统一描述.粘聚模型在界面开始剪切时就发挥作用,摩擦模型在损伤开始时发挥作用.在完全损伤后,粘聚模型完全破坏,界面刚度完全丧失,对剪切应力没有贡献.随后只有摩擦作用在界面发挥作用.该模型不仅描述了界面剪切行为的宏观响应,而且还描述了界面变形过程中的粘结行为和摩擦行为等细观机制.只要得到了界面的相关参数,该模型可以推广到不同材料的其他界面,且易于数值实现.界面条件(如土体性质、温度、含水量或粗糙度)的影响可以耦合在界面参数中.

5 数值结果

何鹏飞等[32]研究了冻土与混凝土界面在不同的温度、含水率和法向压力下的剪切行为,得到了界面的剪切应力-剪切位移关系曲线,本节将使用其文中试验数据对本文构建的界面模型进行验证.图4为典型的试验结果和模型参数(δp、δr、τp、τf).如上所述,模型中的相关参数cp、φp和φr可通过试验结果计算得到.然后通过式(9)或式(11)计算损伤变量D.最后,完整的界面剪切应力-剪切位移演化过程可通过式(10)计算得到.

图4 典型试验结果与模型参数Fig.4 Typical test results and model parameters

表1为通过试验数据计算得到的参数K1和K2.图5为该模型计算结果与试验数据[32]的对比.可以得出,尽管在计算值和试验数据之间存在一些差异,但差异是微不足道的,表明计算结果和试验结果可以很好地匹配.还可以看出,该模型既可以模拟

表1 试验结果中计算到的模型参数Tab.1 Parameters of model from the test results

图5 试验结果与模型计算结果对比

应变软化型曲线又可以模拟应变硬化型曲线.从图5a和表1中可以看出,K1随着初始含水量的增加而减少,而K2则相反.这意味着界面粘聚力随含水率的增大而减小,原因是在-1 ℃和100 kPa时界面只有较少的冰晶存在.如图5b和表1所示,K1随着温度的降低而明显增加,K2则略有降低.表明界面的粘聚力随温度的降低而升高,主要是因为界面胶结冰含量的增加,但温度对摩擦的影响很小[28,32-34].在应变硬化型曲线的拟合中,损伤过程和静摩擦力发展过程为对称的逆相互作用,因此缺少K2的某些数据.在图5c和表1中,由于法向应力对界面粘聚力的影响很小,所以K1随着法向应力的增加而平稳增加[28],而K2随着法向应力的增加而明显增加,这是因为摩擦阻力与摩擦系数和法向压力成正比.

Wang等[33]研究了不同表面粗糙度下冻结粉砂与不锈钢板界面剪切行为,下面使用本文建立的模型与其试验结果进行对比.通过试验数据计算得到的模型参数如表2所示，模型计算结果与试验数据对比如图6所示.可以看出,模型预测结果虽然与试验结果有轻微的差异,但试验数据的主要发展规律和关键参数都能够在模型中反映.造成差异的原因是模型将峰值应力前假设为无损伤的完全弹性变形,而试验中当应力接近峰值时已有一定非线性特征.

表2 试验结果中计算得到的模型参数Tab.2 Parameters of model from the test results

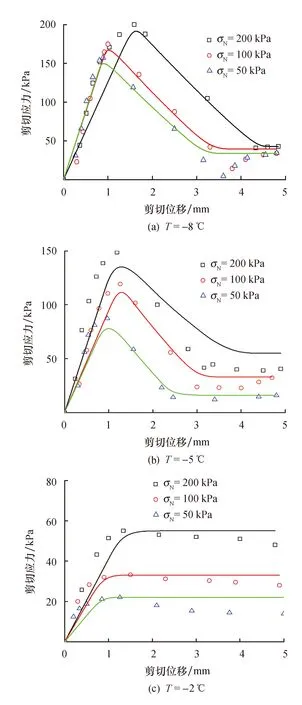
图6 模型预测结果与试验结果对比Fig.6 Comparison of test results and model prediction results

6 结论

1) 建立了冻土与构筑物界面的一维粘聚-损伤-摩擦本构模型,模型基于胶结冰在界面剪切过程中的力学响应及界面出现相对滑动后的摩擦力学特征.将界面微元区域分为损伤部分和非损伤部分,在界面发生相对位移的过程中,微元中非损伤部分假设为弹性变形.在微元由初始的非损伤状态向完全损伤状态变化过程中,摩擦作用随着损伤的发展逐渐发挥作用.

2) 模型以细观的力学演化过程为出发点,进而反映宏观的力学行为.物理假设明确且合理,参数易于确定.模型无需引入塑性软化,将损伤过程和摩擦过程分开考虑增强了模型的灵活性和适用性.

3) 模型既可以模拟应变软化型曲线又可模拟应变硬化型曲线.通过与已有试验数据进行对比发现,虽然模型计算结果与试验数据间存在偏差,但是差异性很小,模型计算结果能够较好地反映试验数据的发展规律和关键参数,模拟结果良好.