NA样本下双指数分布位置参数的经验Bayes估计①

黄金超

(滁州职业技术学院基础部,安徽 滁州239000)

0 引 言

对单参数指数族未知参数的Bayes(EB)统计推断已有相当多的研究,如基于独立同分布(iid)样本下,文献[1-5]讨论了单参数指数族EB估计和检验问题,并得到一些有意义的结论.文献[6]在iid样本下分别讨论了双指数分布参数的EB检验和估计问题,但是在相关样本下双指数分布的参数EB估计问题,据我所知,文中还没有出现,在渗透理论,可靠性分析,以及在某些多元分析等实际问题中,遇到的样本多具有相关性,常见有正相关(PA),负相关(NA).因而,在样本相关的情形下研究双指数分布参数的EB估计问题是非常有意义的.在“平方损失”NA样本下讨论了双指数分布族数的EB估计,构造一渐近最优EB估计函数,在一定条件下,获得EB估计是渐近最优性且收敛速度的阶为O(n-(rs-2)/2(s+2)).推广现有文献中的相应结果.

1 预备知识

首先给出NA样本随机变量(r.v.)序列的定义.定义1.1 随机变量X1,X2,…,X n称为负相关的(NA),如果对于集合{1,2,…,n}的任何两个不交的非空子集A1与A2都有

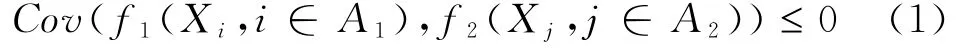
称随机变量序列{X j,j∈N}是负相关的(NA),如果对任何自然数n＞2,X1,X2,…,X n都是负相关的(NA).

考虑如下双指数分布:

此处x∈χ=(-∞,+∞),θ∈Ω=(-∞,+∞),Ω为位置参数空间.

与常见指数分布族等类似,双指数分布族同样是一类应用十分广泛的分布.双指数分布族可用于构造保险精算模型,各种经济模型经常构造双指数模型,另外双指数分布还用于工程技术方面,因此NA样本下研究双指数分布族位置参数的EB估计有重要的理论与实践意义.

设G(θ)为参数θ的未知先验分布,r.v.X的边缘分布密度为

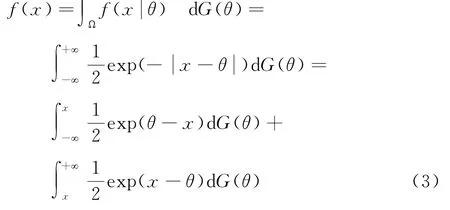
其中G(θ)为θ的未知先验分布.

边缘分布函数记F(x),即

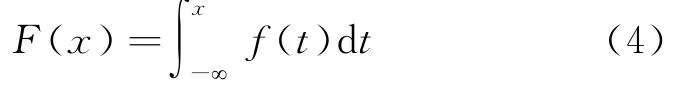
取损失函数为

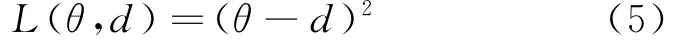
在平方损失(5)下,θ的Bayes估计为

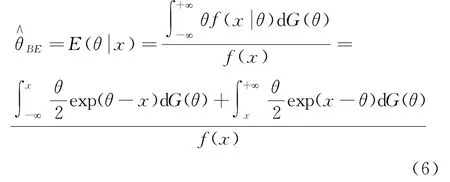
对双指数分布模型(2),在平方损失函数下θ的Bayes估计有下面引理给出.

引理1.1若f(x)＞0,则θ的Bayes估计为其中

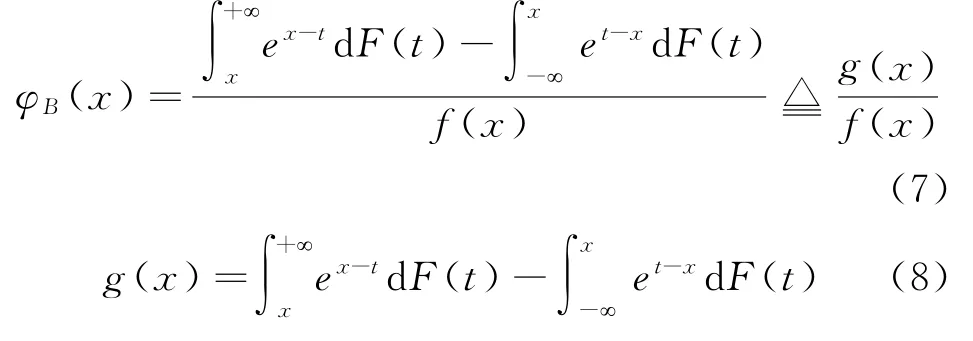
当f(x)=0时,约定

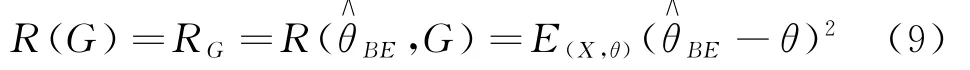
由于先验分布G(θ)的未知,故不能确定,因此无使用价值.从而导致考虑该参数的经验Bayes(EB)估计.

2 经验Bayes(EB)估计

设X1,X2,…,X n和X是同分布NA样本,密度函数如(3)式所示,通常称X1,X2,…,X n为历史样本,称X为当前样本,令f(x)为X1的概率密度函数,假定:

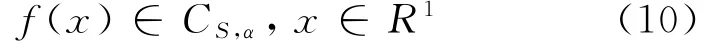
此处C s,α,表示在R1上s阶导数存在,连续且,用

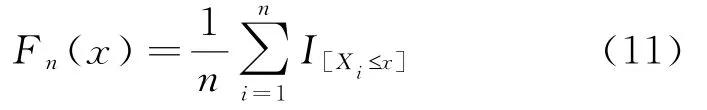
定义为F(x)的估计量.其中I[A]为A的示性函数.类似文献[6]定义g(x)的估计量:

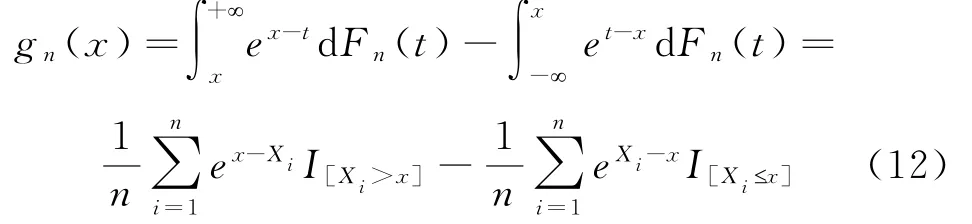
为了估计f(x),引入核函数.令K(x)(r=0,1,…,s-1)为有界的Borel可测函数,在(0,1)之外为0,且满足条件(C):

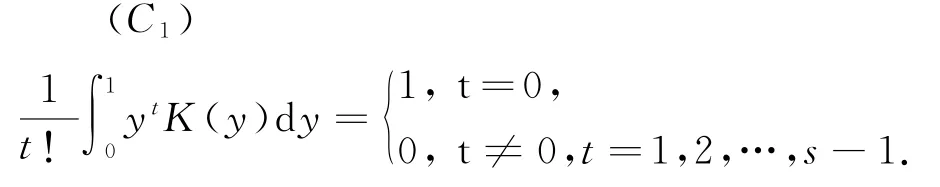
(C2)K(x)在R1上除有限点集E0是可微的,且

对NA序列的协方差作如下假定:

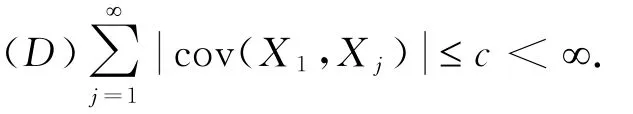
密度函数f(x)的核估计定义为

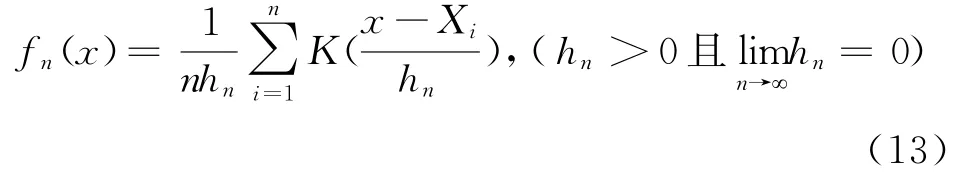
定义θ的EB估计

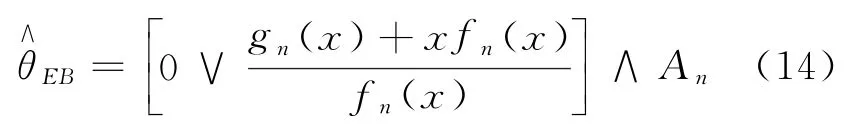
类似文献[5].

这里｛A n｝为正数序列,且=max(a,b),a∧b=min(a,b).

用E*,E n表示对(X1,…,X n,(X,θ)),X1,…,X n联合分布分别求均值.故的全面Bayes风险为

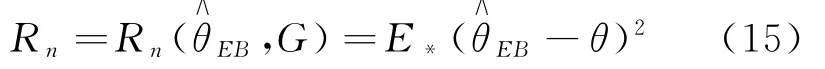
令c,c0,c1,c2…表示不依赖n的正常数.

3 若干引理及主要结果

引理3.1令X,Y是NA样本序列,且方差有限,则对任意的可微函数g1,g2有

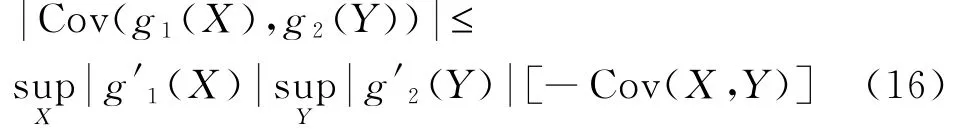
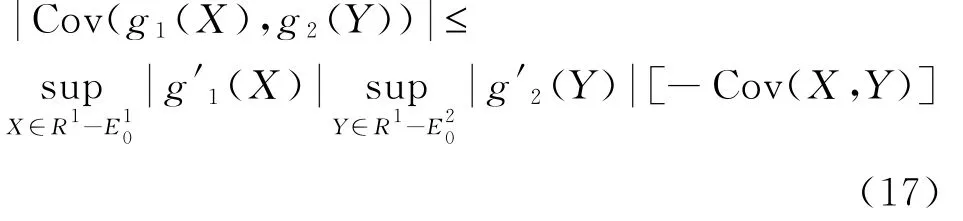
证明见文献[7]引理1

引理3.2设f n(x)由(13)式定义,其中X1,X2,…,X n为NA样本序列,若条件(C)和(D)成立且f(x)∈Cs,α,当取时,对0＜λ≤1有

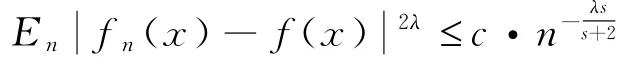
证明见文献[5]定理3.2.

引理3.3若R G＜∞,则对任何EB估计θ∧EB的风险R n有

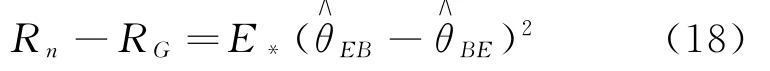
证明见文献Singh[2]引理2.1.

引理3.4对r.v.(Y,Z)和实数y,z≠0,0＜L＜∞且0＜λ≤2,则有

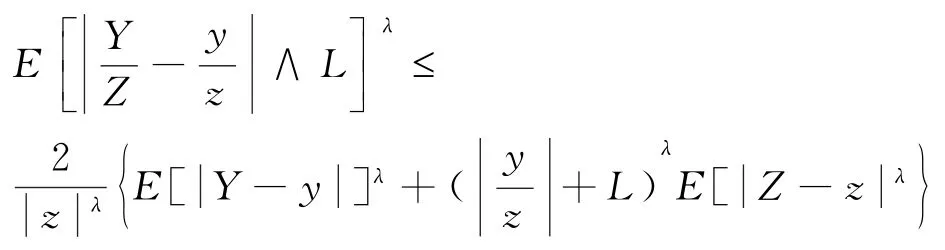
证明见文献[5]引理3.4

引理3.5如果对则对(6)式定义的

证明 由凸函数Jensen不等式可知

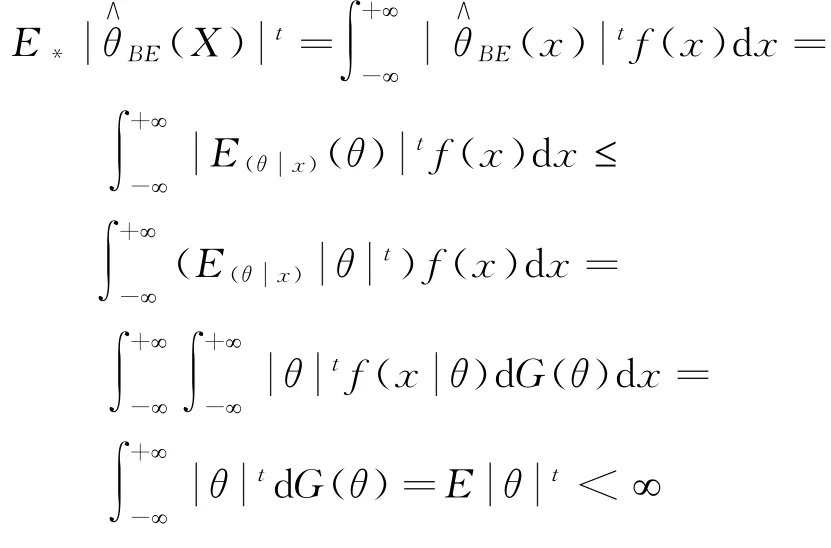
引理3.6设g(x)和g n(x)分别由(8)和(12)式定义,其中X1,X2…,X n NA样本序列,则对0＜r≤2有

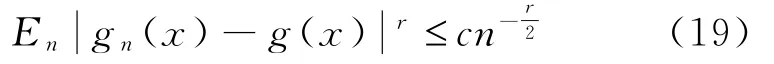
证明类似文献[6]引理3.2的证明

引理3.7若

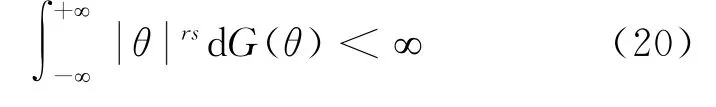
此处s＞1为任意确定的自然数,则对1/2＜r＜1-1/2s,有

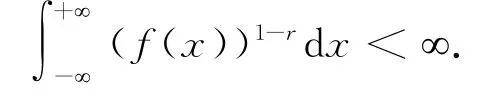
证明见文献[6]引理3.6.

定理3.1设R G,R n分别由(9)和(15)式定义由(14)定义,X1,X2,…,X n为NA样本序列,s＞1的自然数且rs＞2,条件(C)和(D)成立,若

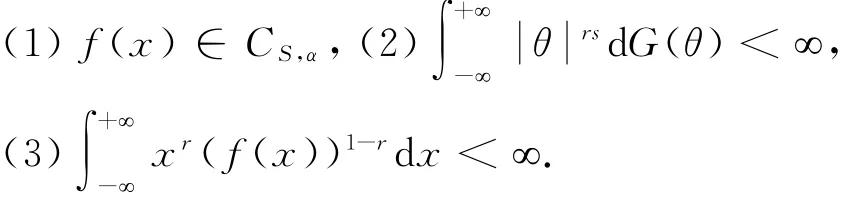
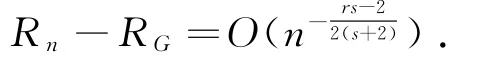
证明由引理3.3和条件(2)可知

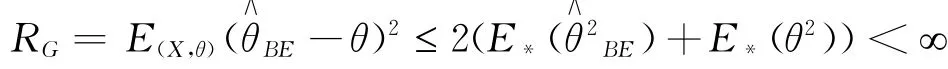
故引理3.3的条件成立,因此有

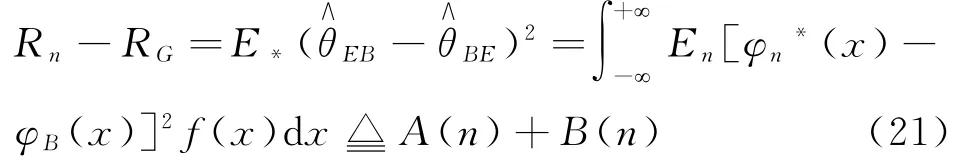
其中

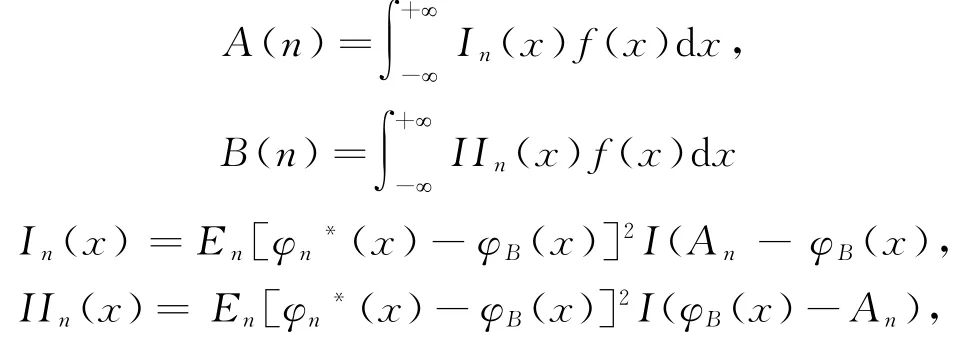
这里I(x)为示性函数:I(x)=1,若x＞0;否则I(x)=0.

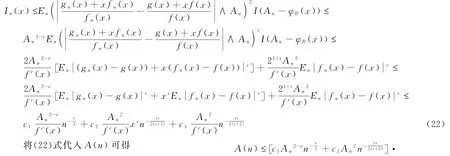
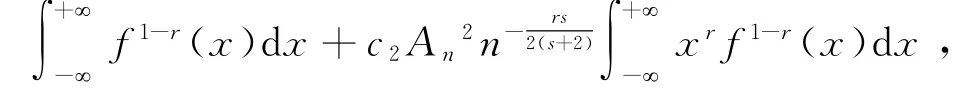
由条件(2)和(3)可得

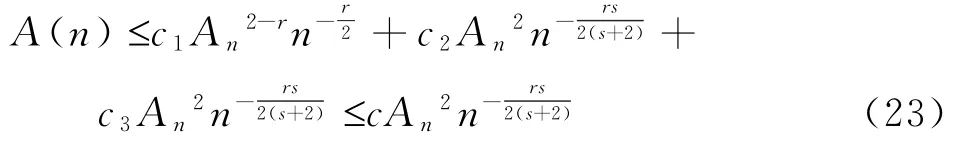
由于0≤φn*(x)≤A n当rs＞2时,有

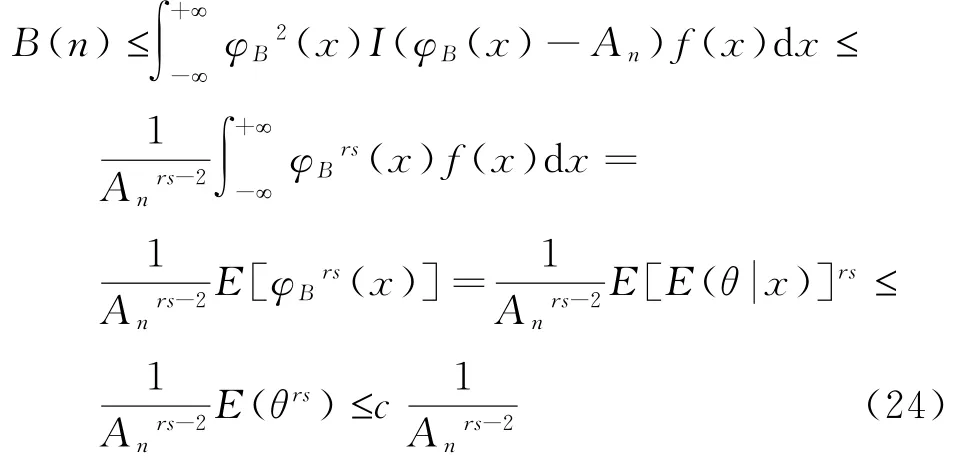
将(23)和(24)式代入(21)可得

取A n=n1/2(s+2)时,可得

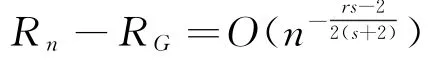
注:与文献[6]比较,比文献[6]多引用了一个NA样本下的引理,定理的证明比文献[6]定理证明简洁些.文献[6]在iid样本下得到收敛速度的阶为比在NA样本下得到收敛速度的阶为略快,与条件较弱有关,当r→1,s→∞,收敛速度阶均近似为O(n-1/2).在NA样本下得到结论比iid样本下更具有一般性,并推广文献[6]的相应结果.