基于演化博弈的共享经济三方主体的参与策略研究

朱峻毅 刘小华

【摘  要】论文构建了包含共享平台、共享资源提供者和消费者3个主体的演化博弈模型，讨论分析各参与主体的演化稳定策略，探讨共享经济模式的发展演化路径，说明代表性因素对博弈主体策略选择的影响，以期为共享经济的良性发展提供参考。

【Abstract】This paper constructs an evolutionary game model including three subjects： sharing platform， sharing resource provider and consumer， discusses and analyzes the evolutionary stability strategies of each participation subject， discusses the development and evolution path of the sharing economy mode， and explains the influence of representative factors on the strategy selection of the game subjects， so as to provide a reference for the benign development of the sharing economy.

【关键词】共享经济;三方主体;演化博弈;参与策略选择

【Keywords】sharing economy; three subjects; evolutionary game; selection of participation strategies

【中图分类号】F713.36;O225                                             【文献标志码】A                                                 【文章编号】1673-1069（2021）11-0065-04

1 引言

2010-2015年共享经济企业的非理性发展，导致很多学者开始思考共享经济是否存在不同于传统经济的新规律。已有部分学者运用博弈论的方法对共享经济问题展开了研究。例如，王洪利（2018）进行了基于演化博弈的消费者和商家租赁、共享行为的分析;刘珺（2017）以出行者和政府作为博弈对象，構建了出行者与政府策略选择的演化博弈模型;丁茂森等（2017）基于博弈论的角度，运用纳什博弈均衡的方法对目前共享单车公司的激烈竞争进行分析;全雄伟（2018）通过运用演化博弈理论对共享单车的竞争机制进行分析，发现共享单车存在恶性竞争的问题。现有的研究基本是针对共享经济型企业/平台（以下简称“平台”）、共享资源提供者和消费者3个主要参与主体，选取1个或者2个进行其行为策略的分析，缺乏从博弈论视角研究三者之间的冲突与合作问题。

2 共享经济主体的参与策略演化博弈模型构建

2.1 主体参与策略演化模型的假设

为有效地开展演化博弈模型的研究，需要对模型进行一些必要的假设。假设1：各博弈参与主体是有限理性、有限信息的。假设2：假设共享平台有2种策略选择，即对消费者与资源提供者进行补贴或不补贴。为简化模型，假设对二者的补贴是同步的，即同时补贴或者同时不补贴;且补贴是以优惠券或红包的形式预先给到消费者及资源提供者手中。假定共享平台补贴会促进资源提供者与消费者参与到闲置资源的共享与租赁中，使得共享平台的市场份额扩大，收益增加。假设3：假设资源提供者在资源共享前没有收益，其策略有2种，即提供出租资源或不提供出租资源。资源提供者提供共享资源时，一般需要对其投入一定的改造成本。假设4：假设消费者有2种策略，即选择共享平台提供的租赁服务或选择传统服务，实现自身的需求。假设5：补贴机制下，考虑共享平台、资源提供者与消费者的收益变化因素，剔除不变化的量，设定三者的收益方程为：共享平台收益=营业效益+衍生效益-成本;资源提供者收益=营业效益-成本消费者收益=服务价值-成本。

2.2 主体参与策略演化模型参数的选择与设定

在模型假设的基础上，定义如下模型中用到的参数：

C0——共享平台提供共享资源服务所投入的基本运营成本;S0——资源提供者为加入共享平台而进行的一次性改造的成本，如营业执照的获取、设备的改装等费用;Cs——资源提供者提供共享服务的运营成本;Q0——共享平台未提供补贴时的基本需求量;P0——消费者在无共享资源可用的情况下采用自购或者传统商家的服务产生的支付价格;Pc——消费者租赁资源提供者的资源支付给共享平台的价格;Ps——共享平台租赁资源提供者的资源所支付的价格;Dc——当消费者租赁共享平台提供的资源时，共享平台给消费者的补贴价格;Ds——当资源提供者在平台上共享自有资源时，共享平台给资源提供者的补贴价格;R0——消费者在无共享资源可用的情况下采用自购或者传统商家的服务产生的功能性收益;B0——消费者在无共享资源可用的情况下采用自购或者传统商家的服务产生的心理性损益;Rc——消费者在租赁共享资源后产生的功能性收益，R0+Dc≥Rc;Bc——消费者在租赁共享资源后产生的心理性损益;L——共享平台不提供补贴策略的机会损失，由于市场竞争激烈，共享平台不提供补贴，消费者在综合考虑收益及安全性等方面后不会选择，消费者选择传统商家，而获得的衍生收益函数;Ls——资源提供者不共享资源的机会损失，包含潜在的收益，如在汽车共享中未获得的利润、加油费优惠等损失;Lc——消费者选择共享平台，但是由于资源提供者没有共享资源而损失的收益，包含浪费的时间成本及由此带来的潜在损失等;θ——共享平台提供补贴而获得的需求量增加的函数，假设当共享平台提供补贴，会有效刺激更多的资源提供者分享自己的资源，同时会吸引更多的消费者选择共享平台提供的资源，共享平台需求量增加，补贴越大需求量越大，令θ为随补贴力度而变化的函数，即当补贴为D时，需求量增加θ（D）;δ——共享平台提供补贴而获得的衍生收益函数，主要指由于共享平台对外宣传提供补贴策略而获得的声誉及潜在的市场机会的收益，补贴越大收益越高，即当补贴为D时，衍生收益为δ（D）;x——共享平台选择“补贴”策略的比例;y——资源提供者择“共享”策略的比例;z——消费者选择“租赁”策略的比例，0≤x，y，z≤1。

2.3 主体参与策略演化模型的构建

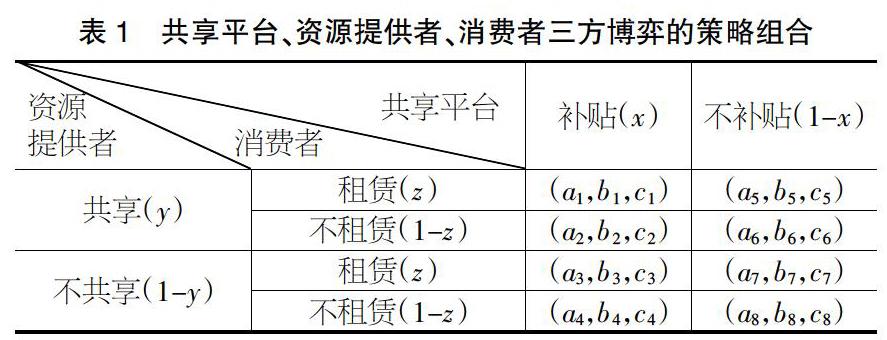
由于共享经济博弈的三方主体会通过学习、模仿进行策略选择，使得x、y、z发生变化。在模型假设的基础上，将共享平台“补贴”与“不补贴”、资源提供者“共享”与“不共享”、消费者“租赁”与“不租赁”的策略进行组合，如表1所示。

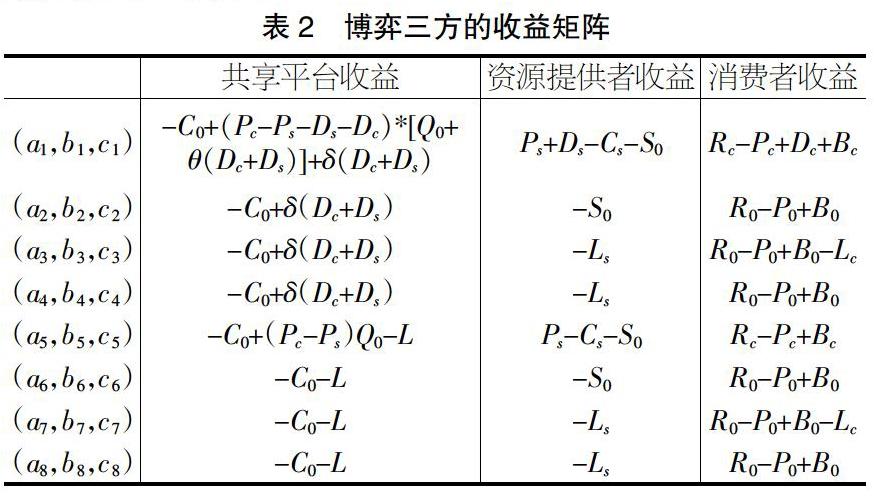
根据表1的策略选择，给出共享经济的三方主体的收益矩阵，如表2所示。

3 共享经济主体的参与策略演化博弈均衡分析

3.1 主体参与策略演化博弈的期望收益函数构建

根据表2的收益矩阵，可得共享平台、资源提供者、消费者三方主体的期望收益如下。

3.1.1 共享平台的期望收益函数

令共享平台选择补贴时的期望收益为Ux，共享平台选择不补贴时的期望收益为U1-x，则共享平台的平均期望收益为，则=xUx+（1-x）U1-x，其中：

Ux=yz{-C0+（Pc-Ps-Ds-Dc）[Q0+θ（Dc+Ds）]+δ（Dc+Ds）}+y（1-z）*      [-C+δ（Dc+Ds）]+（1-y）z[-C0+δ（Dc+Ds）]+（1-y）（1-z）[-C0+δ（Dc

+Ds）]

U1-x=yz[-C0+（Pc-Ps）Q0-L]+y（1-z）（-C0-L）+（1-y）z（-C0-L）+（1-y）（1-z）（-C0-L）

3.1.2 資源提供者的期望收益函数

令资源提供者选择共享的期望收益为Uy，共享平台选择不补贴时的期望收益为U1-y，则共享平台的平均期望收益为，则=yUy+（1-y）U1-y，其中：

Uy=xz（Ps+Ds-Cs-S0）+x（1-z）（-S0）+（1-x）z（Ps-Cs-S0）+（1-x）（1-z）（-S0）

U1-y=xz（-Ls）+x（1-z）（-Ls）+（1-x）z（-Ls）+（1-x）（1-z）（-Ls）

3.1.3 消费者的期望收益函数

令消费者选择租赁的期望收益为Uz，共享平台选择不补贴时的期望收益为U1-z，则共享平台的平均期望收益为，则=zUz+（1-z）U1-z，其中：

Uz=xy（Rc-Pc+Dc+Bc）+x（1-y）（R0-P0+B0-L0）+（1-x）y（Rc-Pc+Bc）+（1-x）（1-y）（R0-P0+B0-Lc）

U1-z=xy（R0-P0+B0）+x（1-y）（R0-P0+B0）+（1-x）y（R0-P0+B0）+（1-x）（1-y）（R0-P0+B0）

3.2 主体参与策略演化博弈的复制动态方程与均衡分析

3.2.1 共享平台的复制动态方程与均衡分析

根据Malthusian动态方程，共享平台的复制动态方程为：F（x）==x（1-x）{yz[（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）]+δ（Dc+Ds）+L}。

令F（x）=0，解得x*=0，x*=1，y*=。则有：Fx'（x）==（1-2x）{yz[（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）]+δ（Dc+Ds）+L}成立。由复制动态微分方程的稳定性定理及演化稳定策略可知，当F（x）=0，Fx'（x）<0时，x*为演化稳定策略。现讨论如下：

①当y*=时，有F（x）=0恒成立。这表明所有水平都是稳定状态，即此时策略选择比例不会随时间的推移而变化。

②当（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）>0时，易知：δ（Dc+Ds）>0，L>0，y≥0，z≥0。进而有：yz[（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）]+δ（Dc+Ds）+L>0，则可以得到Fx'（0）>0，Fx'（1）<0，所以x=1是平衡点。这说明共享平台在进行补贴之后，实际得到的营业利润大于其不补贴时获得的营业利润，共享平台倾向于选择补贴策略。

③当（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）<0时：

由复制动态微分方程的稳定性定理及演化稳定策略可知，当F（z）=0，Fz'（z）<0时，z*为演化稳定策略。现讨论如下：

4 共享经济主体策略的稳定性与演化结果分析

4.1 共享经济主体的参与策略演化博弈的稳定性分析

按照Hirshleifer的概念，下面根据雅克比矩阵定性分析系统在这些均衡点的局部稳定性。首先给出雅克比矩阵如下：

J=a11 a12 a13a21 a22 a23a31 a32 a33

综上可知，系统存在8个特殊的均衡点，分别为（0，0，0）（0，1，0）（0，0，1）（0，1，1）（1，0，0）（1，1，0）（1，0，1）（1，1，1）。另外，存在由x*、y*、z*与x=0或1，y=0或1，z=0或1组成的特殊点。下面分别讨论上述8个点与其他特殊点的渐近稳定性。

当8个点都代入雅克比矩阵时，都有a12、a13、a21、a23、a31、a32为0，则a11、a22、a33为该雅克比矩阵的特征值。根据李雅普诺夫间接法可知，当矩阵的3个特征值均为负数时，均衡点为演化稳定策略;当它们均为正数时，均衡点为不稳定点;当它们中有1个或2个为正数时，均衡点为鞍点。

分别分析上述8个点，具体如下：

①将（0，0，0）（0，0，1）（0，1，0）代入矩阵时，都有a11>0，则该3点都为不稳定点。②将（1，0，1）代入矩阵时，都有a33>0，则该点都为不稳定点。③将（1，0，0）代入矩阵时，有矩阵的2个特征值，a11<0，a33<0，当有a22<0成立，则（1，0，0）为均衡稳定策略。若要a22<0，必有-S0+Ls<0。④同理可得，系统在（0，1，1）时的雅克比矩阵时，需满足稳定条件I。即条件I：{（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）+δ（Dc+Ds）+L<0，-S0+Ls+Ps-Cs>0，Rc-Pc+Bc-R0+P0-B0>0}。⑤系统在（1，1，0）时的雅克比矩阵时，有α11<0，若满足稳定条件II：即条件II：{-S0+Ls>0，Rc-Pc+Bc-R0+P0-B0+Dc<0}，则（1，1，0）为渐近稳定点。⑥系统在（1，1，1）时的雅克比矩阵时，若满足稳定条件III：即条件III：{（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）+δ（Dc+Ds）+L>0，-S0+Ls+Ps-Cs+Ds>0，Rc-Pc+Bc-R0+P0-B0+Dc>0}，则（1，1，1）为渐近稳定点。⑦由x*、y*、z*与x=0或1，y=0或1，z=0或1组成的特殊点的渐近稳定性分析如下：

首先，當满足

yz[（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）]+δ（Dc+Ds）+L=0y（1-y）=0z（1-z）=0时，假定方程组存在解（x1，y1，z1），则系统在（x1，y1，z1）不存在渐近稳定点。

同理，当满足

x（1-x）=0-S0+Ls+z（Ps-Cs）+xzDs=0z（1-z）=0和x（1-x）=0y（1-y）=0y（R0-Pc+Bc-Rc+P0-B0）+xyDc=0时，易知此矩阵行列式值为0，故必有一个特征值为0，所以可知系统也不存在渐近稳定点。

其次，当满足

yz[（-Dc-Ds）Q0+（Pc-Ps-Dc-Ds）θ（Dc+Ds）]+δ（Dc+Ds）+L=0-S0+Ls+z（Ps-Cs）+xzDs=0z（1-z）=0时，雅克比矩阵此时必有一个非负特征值，故不存在渐近稳定点。根据上述证明，（x*，y*，z*）不是演化博弈矩阵的ESS。

总结上述分析，可得以上点的渐近稳定性，如表3所示。

根据系统演化博弈均衡解及实现条件，可以得出以下分析结果：首先，共享平台为折扣支付的成本能够被其增长的收入覆盖时，如（1，0，0）（1，1，0）和（1，1，1）3个策略组合，共享平台选择提供共享服务及提供折扣。且当收入增长越多时，共享平台收敛到补贴策略的速度越快。其次，目标消费者如果在选择共享服务中获得收益大于其在传统服务中获得的收益，如组合策略（0，1，1）和（1，1，1），则消费者会选择共享服务。如果其收益相对较高时，他们不会特别重视共享平台的补贴，仍旧会选择加入共享策略。但如收益不高，则会选择传统策略。消费者的收益包含物质收益及心理收益，如共享平台提供的便利性、独特性及其服务的异质性。因此，共享平台与资源提供者可以通过提高服务水平来提升双方的收益。收益水平越高，消费者选择该策略的概率越大。三方的参与策略也越快速地收敛到（1，1，1）策略。最后，资源提供者如能在共享资源中获得收益，且其收益可以弥补其为之投入的成本，他们会选择参加共享服务，如（1，1，0）和（1，1，1）策略组合。共享平台对于资源提供者的资质与服务提出相应的要求，即准入门槛。当准入门槛较低时，资源提供者越愿意出借资源;相反则越低。除此之外，共享平台对于资源的收费越高，越不利于促进共享经济的发展，没有资源愿意加入，则无法形成资源的有效流动。

4.2 共享经济主体的参与策略的演化结果分析

通过上述分析，可以发现共享经济3个主体间关系处于动态过程，共享经济是否能够良性发展，不仅取决于消费者消费意愿，还取决于资源提供者的意愿。引导二者是否能够资源分享，取决于核心企业——共享平台策略选择与引导。共享经济发展的健康有序，更应该注重政府监管政策的制定与引导，从而实现共赢。

【参考文献】

【1】王洪利.基于演化博弈的共享经济参与主体的行为分析[J].经济与管理，2018，32（2）：75-80.

【2】刘珺.汽车共享出行模式选择的演化博弈研究[D].南京：南京大学，2017.

【3】丁茂森，任如愿.基于博弈论的共享单车企业竞争策略选择分析[J].现代商业，2017（20）：107-108.

【4】全雄伟.共享单车竞争机制演化博弈分析与仿真[J].广东开放大学学报，2018，27（2）：99-103.

【5】张春媚.基于价值网的共享经济下服饰租售商业模式研究[J].东南大学学报（哲学社会科学版），2017，19（S2）：115-118.

【6】罗煜.新经济视角下华南城商业模式创新研究[J].商业经济研究，2017（10）：120-122.

【7】傅永军.公共领域与合法性——兼论哈贝马斯合法性理论的主题[J].山东社会科学，2008（3）：5-11.