T91/TP347H异种钢焊接接头过热工况下蠕变损伤模型研究

金震杰，刘川槐，曹 宇,陆一帆,潘卫国，纪冬梅

(1.上海电力大学 能源与机械工程学院，上海 200090；2.淮浙电力有限责任公司 凤台发电分公司,安徽淮南 232131)

0 引言

为了节能环保及提高发电效率，超(超)临界火力发电机组已经成为电力行业的主要发电机组，蒸汽的热力参数随之不断地提高，这也相应地对锅炉、汽轮机的金属材料安全性提出了更高的要求。其中以T91和T92为主的铁素体钢[1]与TP347H，Super304H和HR3C为主的奥氏体钢[2]被广泛用于超(超)临界机组的锅炉中。在锅炉的过热器与再热器管道中，由于各部分连接管道对于材料的抗蠕变性、导热性和耐腐蚀性的要求不同，以及成本、操作等问题，所以在管道连接处出现了大量铁素体钢和奥氏体钢异种钢焊接接头[3]。在高温高压的苛刻条件下服役，异种钢焊接接头由于残余应力[4]、热腐蚀[5-6]和蠕变破坏[7]等作用容易发生早期失效。据统计，由锅炉内过热器与再热器等位置的炉管失效而导致的事故占总事故的2/3[8]，其中，过热是造成过热器与再热器管道失效的一个重要原因[9]。在超(超)临界火力发电机组内，管道长期过热，不仅会使异种钢焊接接头产生蠕变损伤[10]，而且严重时会发生管道爆管[11]。目前，对于T91/TP947H异种钢焊接接头的研究，主要集中在微观组织分析[12]、力学性能测试[13]和失效原因分析[14-15]，而对于这种材料的损伤计算与寿命预测缺乏相应的研究。在许多情况下，蠕变损伤与长期过热可以说是等同的[16]，所以对异种钢焊接接头进行超温工况下的蠕变损伤计算与精准寿命预测是保证设计制造与安全运行的关键[17]，具有重大意义。

对于金属材料的蠕变损伤计算方面，专家学者提出过很多蠕变损伤模型，较为普遍的有等温线外推法[18]、Larson-Miller公式[19]、Norton定理[20]、Norton-Bailey定理[21]、Monkman-Grant方程[22]、θ参数法[23]、修正θ参数法[24]和连续损伤力学(Continuum Damage Mechanics)[25]等，总的来说，这些蠕变损伤模型可以分为应力损伤和应变损伤两类[26]。等温线外推法、Larson-Miller公式和连续损伤力学属于从应力角度出发的应力损伤模型，其中以Kachanov和Rabotnov的理论发展而来的连续损伤力学使用最为普遍，基于两人提出的Kachanov-Rabotnov方程是众多蠕变本构模型的基础。Larson-Miller公式则因其简便的形式在工程中有较多的应用。在应变损伤模型中，从应变方向出发，Norton-Bailey定理可以用来描述蠕变的第一阶段，Norton定理和Monkman-Grant方程则多用来描述蠕变的第二阶段。θ参数法则能描述整个蠕变三阶段，然而此模型与材料自身性质、温度和应力有关，对于材料不同的异种钢焊接接头使用会有一定的局限性[27]。

本文通过对T91/TP347H异种钢焊接接头在超温工况下进行蠕变试验，基于试验结果，分别采用非线性连续损伤力学模型、应力损伤模型中常用的Kachanov-Rabotnov模型(K-R模型)和应变损伤模型中常用的Norton定理拟合材料参数，并对试样在这三种模型下进行损伤计算、蠕变应变分析与寿命预测，最后将计算结果结合试验数据进行比较，分析各个模型的优缺点，为T91/TP347H异种钢焊接接头超温运行下的损伤计算与寿命预测提供参考。

1 试验材料与蠕变试验

本文针对T91/TP347H异种钢焊接接头，开展蠕变试验。试样由未服役的T91/TP347H异种钢焊接接头加工而成，接头为∅45 mm×12 mm的管材，采用氩弧焊焊接，使用的填充材料为ERNiCr-3，接头母材及中间焊缝材料的化学成分分别见表1～3。将试样加工为标准试样，结构尺寸如图1所示。

表1 SA213-T91钢的化学成分

表2 SA213-TP347H钢的化学成分

参考GB/T 2039—2012《金属材料 单轴拉伸蠕变试验方法》设计试验方案(见表4)。在高温蠕变持久试验机(GWT2504)上，对试样进行高温单轴蠕变试验，试验结果见表4，试样见图2。

表3 ERNiCr-3的化学成分

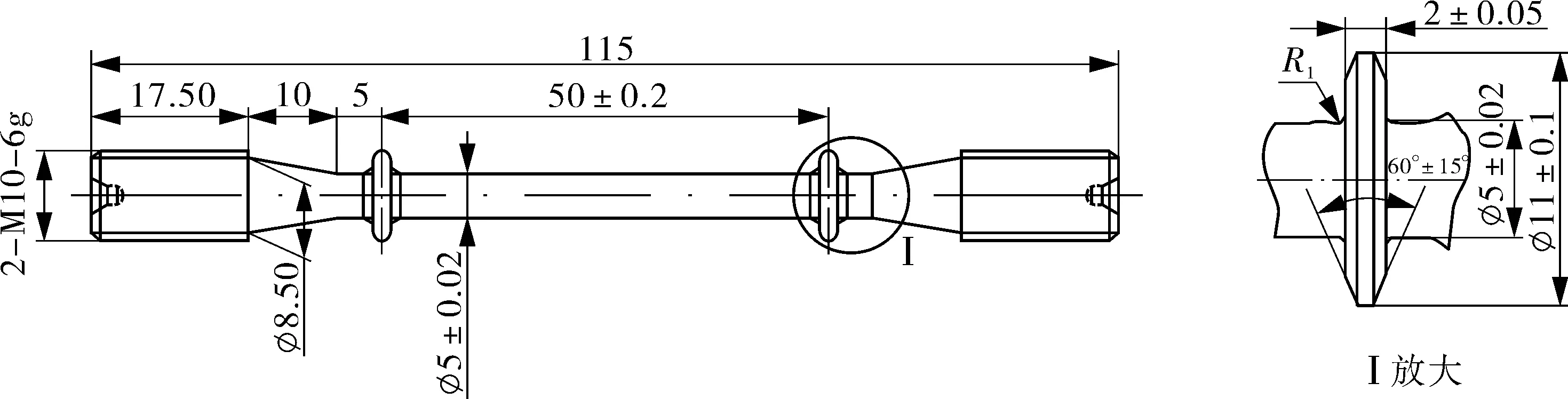
图1 试样结构尺寸

表4 T91/TP347H异种钢焊接接头的蠕变试验方案及结果

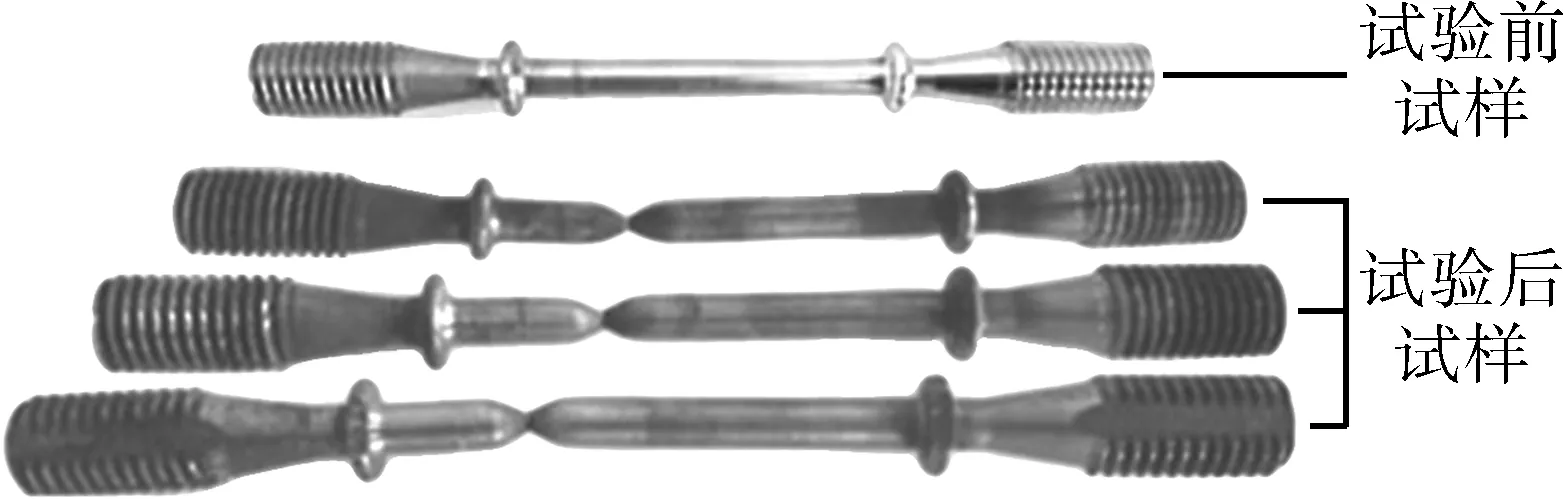
图2 试验前后的试样

根据试验结果可计算T91/TP347H异种钢焊接接头在不同试验方案下的蠕变应变，如图3所示。

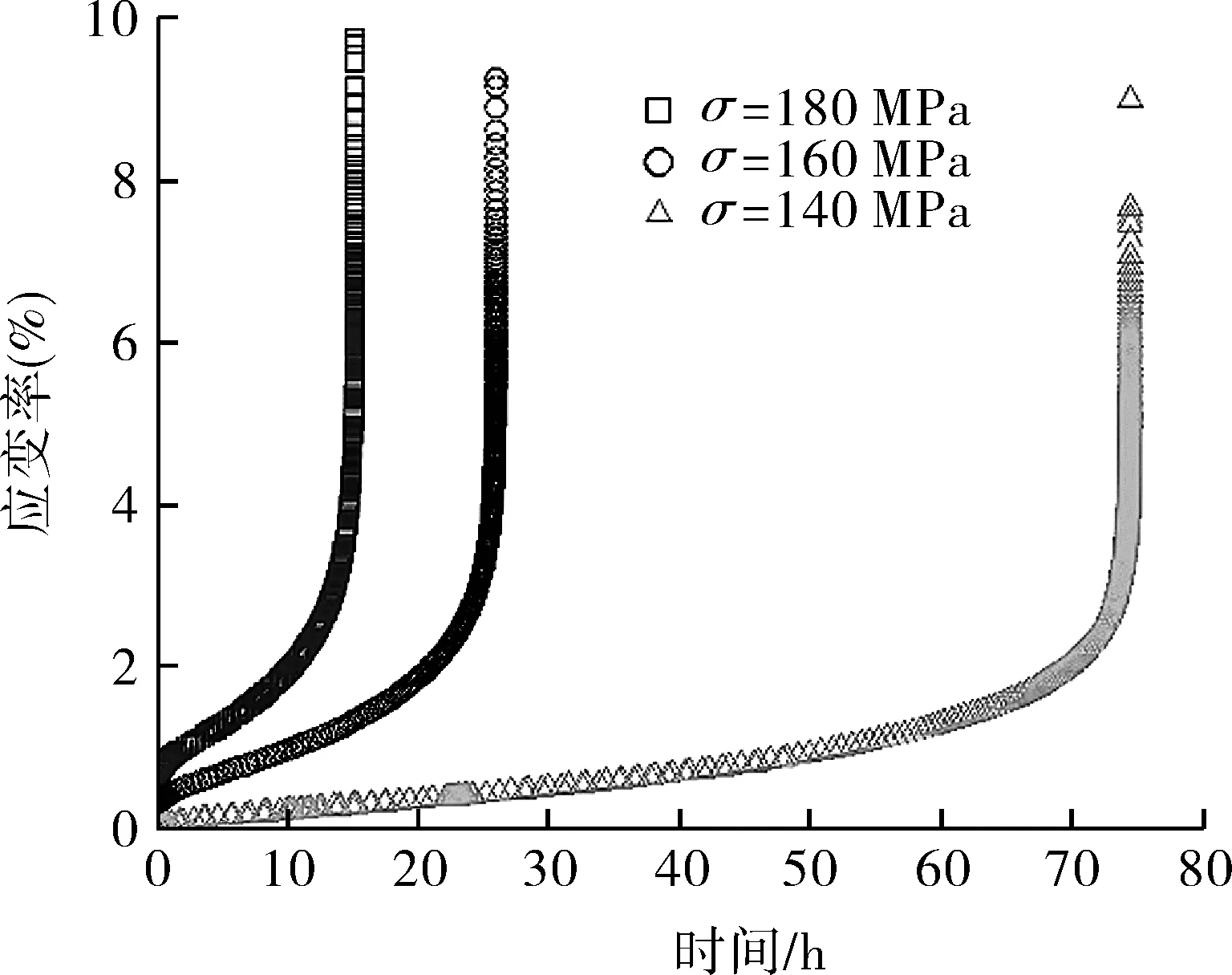
图3 T91/TP347H在不同应力下的蠕变应变

2 T91/TP347H异种钢焊接接头蠕变损伤本构模型

2.1 Norton模型

在整个蠕变过程中，其蠕变第二阶段的蠕变寿命占到了整个寿命的70%以上，因而大多蠕变本构模型描述的都是蠕变第二阶段，其中Norton定理使用最为广泛，其形式如下：

(1)

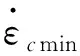
对式(1)两边取对数，改写为：

(2)

通过试验数据拟合出n和lnA,其拟合结果如图4所示。

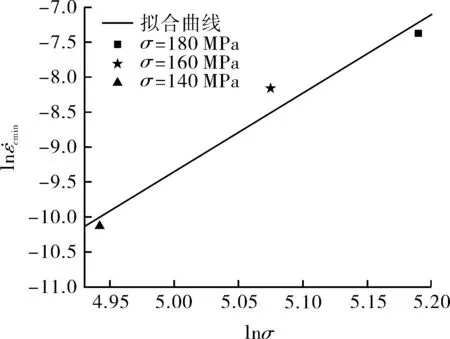
图4 Norton模型拟合曲线

文献[28]中提出Monkman-Grant方程，该方程表示材料最小蠕变速率与断裂时间的关系：

(3)

式中，i为材料参数;tr为断裂时间；C为Monkman-Grant常数。

同样地，利用试验数据对其进行拟合，得到参数C和i，拟合结果如图5所示。

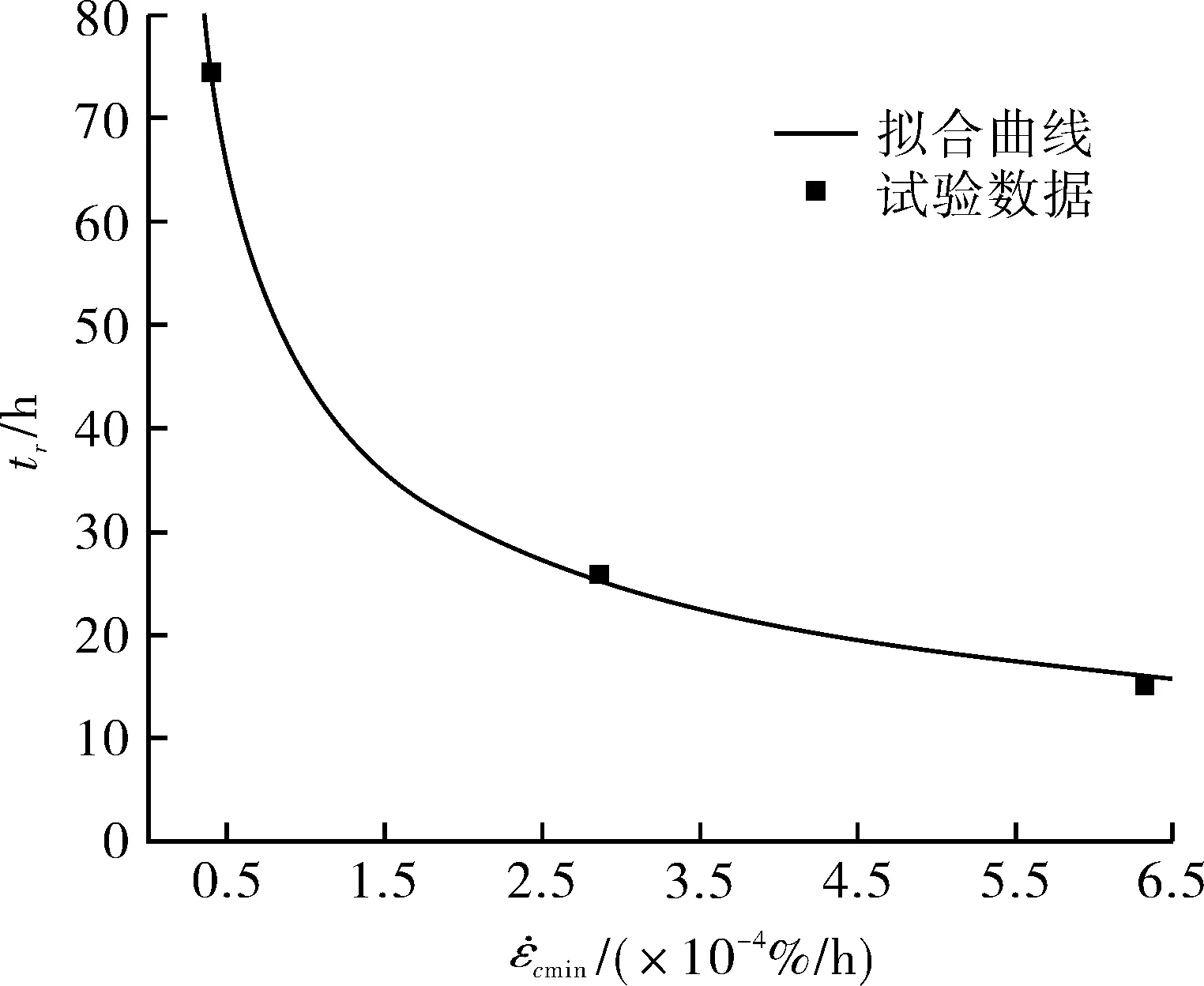
图5 Monkman-Grant方程拟合曲线

由式(1)(3)可以得到基于Norton定理和Monkman-Grant方程的蠕变断裂时间预测模型：

(4)

针对T91/TP347H异种钢焊接接头，模型所有参数见表5。

表5 Norton模型和Monkman-Grant方程材料参数

2.2 Kachanov-Rabotnov模型与方程材料参数拟合

KACHANOV[29]最早提出了连续损伤力学(CDM)的概念，将材料的损伤用连续性因子来表示，RABOTNOV[30]在此基础上将损伤与蠕变速率耦合在一起，提出了经典的Kachanov-Rabotnov蠕变损伤本构模型：

(5)

(6)

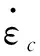
对式(6)两边进行积分，取时间t=0时，D=0为初始值，得到蠕变断裂时间t的表达式：

(7)

将t=tr时，D=1代入，得：

(8)

根据式(7)(8)可以得到：

(9)

将式(9)代入式(5)中，两边积分，得到蠕变应变与时间的关系式：

(10)

在式(10)中，当t=tr时，损伤D=1，则蠕变断裂应变为：

(11)

将式(10)与式(11)相除，得到蠕变应变εc、蠕变断裂应变εr比值和蠕变时间t、蠕变断裂时间tr比值的关系式：

(12)

为了方便拟合参数，首先将式(8)改写为：

tr=Kσβ

(13)

式中，K=[B(1+α)]-1,β=-m。

根据试验结果中施加应力与断裂时间，对式(13)进行拟合，求出K和β，其拟合结果见图6。

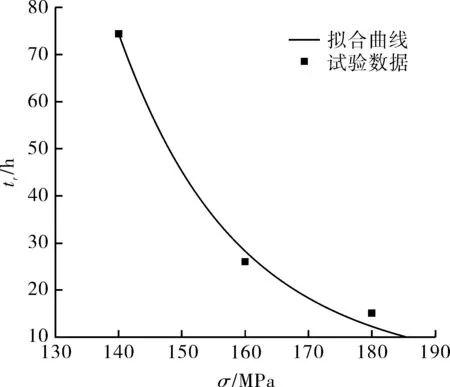
图6 断裂时间与应力关系曲线

再利用式(12)拟合T91/TP347H异种钢焊接接头在试验条件下的蠕变应变与蠕变时间的关系。理论上，在温度相同的情况下，不同应力的蠕变试验拟合出的指数是相同的，但实际每组试验都会有不同的偏差，所以不同的试验结果有着不同的拟合结果，现将3组试验数据整合在一起拟合出一个最佳的结果，拟合结果如图7所示。

对于材料参数中的A与n，可采用Norton模型的拟合参数[31]，进而求出α和B。以上所有Kachanov-Rabotnov蠕变损伤本构方程材料参数的计算结果如表6所示。

表6 Kachanov-Rabotnov模型材料参数

2.3 非线性连续损伤力学模型

2.3.1 双参数非线性蠕变连续损伤力学模型

对于连续损伤力学，基于KACHANOV的损伤理论，早期提出了用来描述蠕变损伤行为状态的公式[32]：

(14)

式中，λ，r为材料参数。

取t=0时，D=0为初值，对式(14)进行积分，得到：

(15)

将t=tr时，D=1代入，得:

(16)

再对式(14)进行微分，得到其蠕变损伤增量与时间增量的关系式：

(17)

此模型公式中包括了2个材料参数，文中称为双参数非线性蠕变连续损伤力学模型。

2.3.2 三参数非线性蠕变连续损伤力学模型

LEMAITRE[33-34]提出了有3个材料参数的多轴蠕变损伤模型：

(18)

式中，Rv为三轴度因子;α2,λ,r为材料参数。

单轴情况下Rv=1时：

(19)

当t=tr时,D=1，将其代入式(19)，得：

(20)

对式(19)进行微分，同样得到蠕变损伤增量与时间增量的关系式：

(21)

此时该模型中有3个材料参数，本文称为三参数非线性蠕变连续损伤力学模型。

2.3.3 模型材料参数的拟合

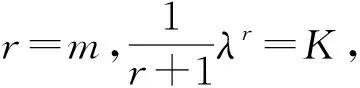
3 非线性连续损伤力学模型、Norton模型与Kachanov-Rabotnov模型的比较

3.1 各模型下蠕变应变的分析

对于用来描述材料单轴应力状态下的蠕变过程，Norton模型和Kachanov-Rabotnov模型都能通过相应的公式来表示蠕变过程。其中对式(1)进行积分，得到：

εc=Aσnt+K

(22)

式中，K为蠕变第二阶段变形率。

Kachanov-Rabotnov模型则利用式(10)来描述其单轴蠕变的过程。其中，材料参数α需要根据不同应力的情况选取拟合值，具体取值如表7所示。

表7 Kachanov-Rabotnov模型材料参数α的取值

非线性连续损伤力学模型只能从损伤角度来描述整个蠕变过程，无法从蠕变应变角度给出比较，现将Norton模型和Kachanov-Rabotnov模型在施加不同应力下的蠕变过程曲线进行比较与分析，其结果如图8所示。

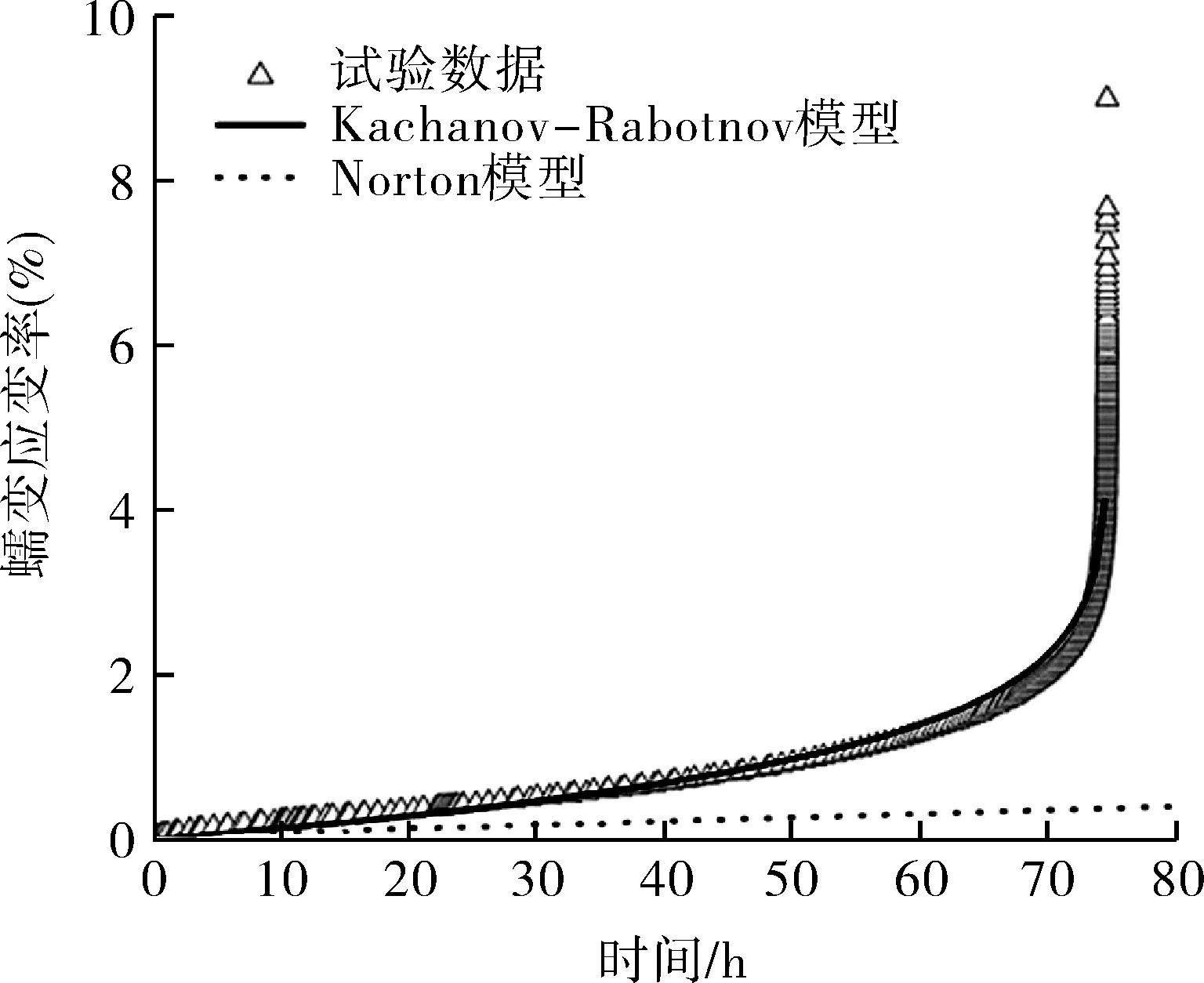
(a)σ=140 MPa

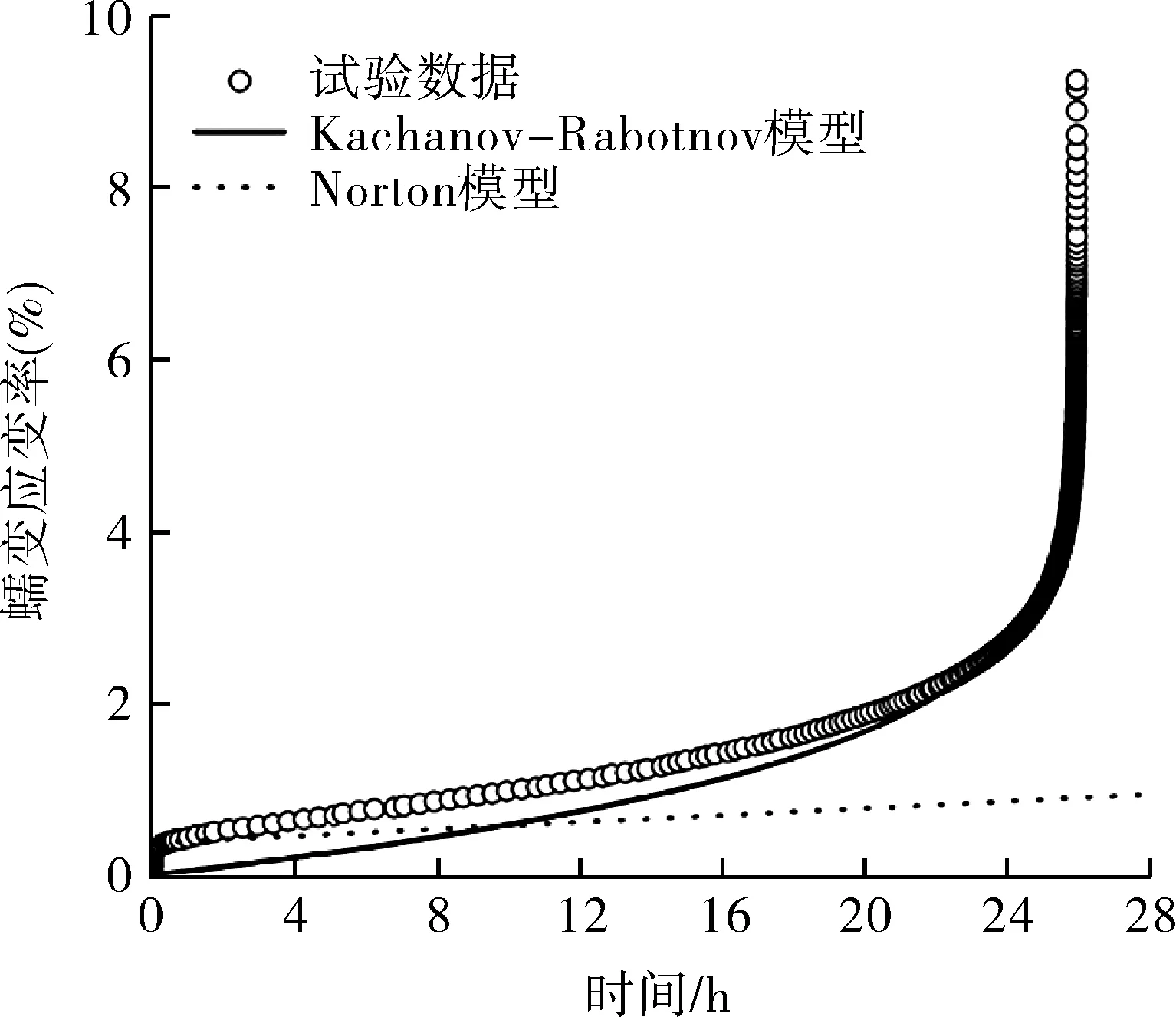
(b)σ=160 MPa

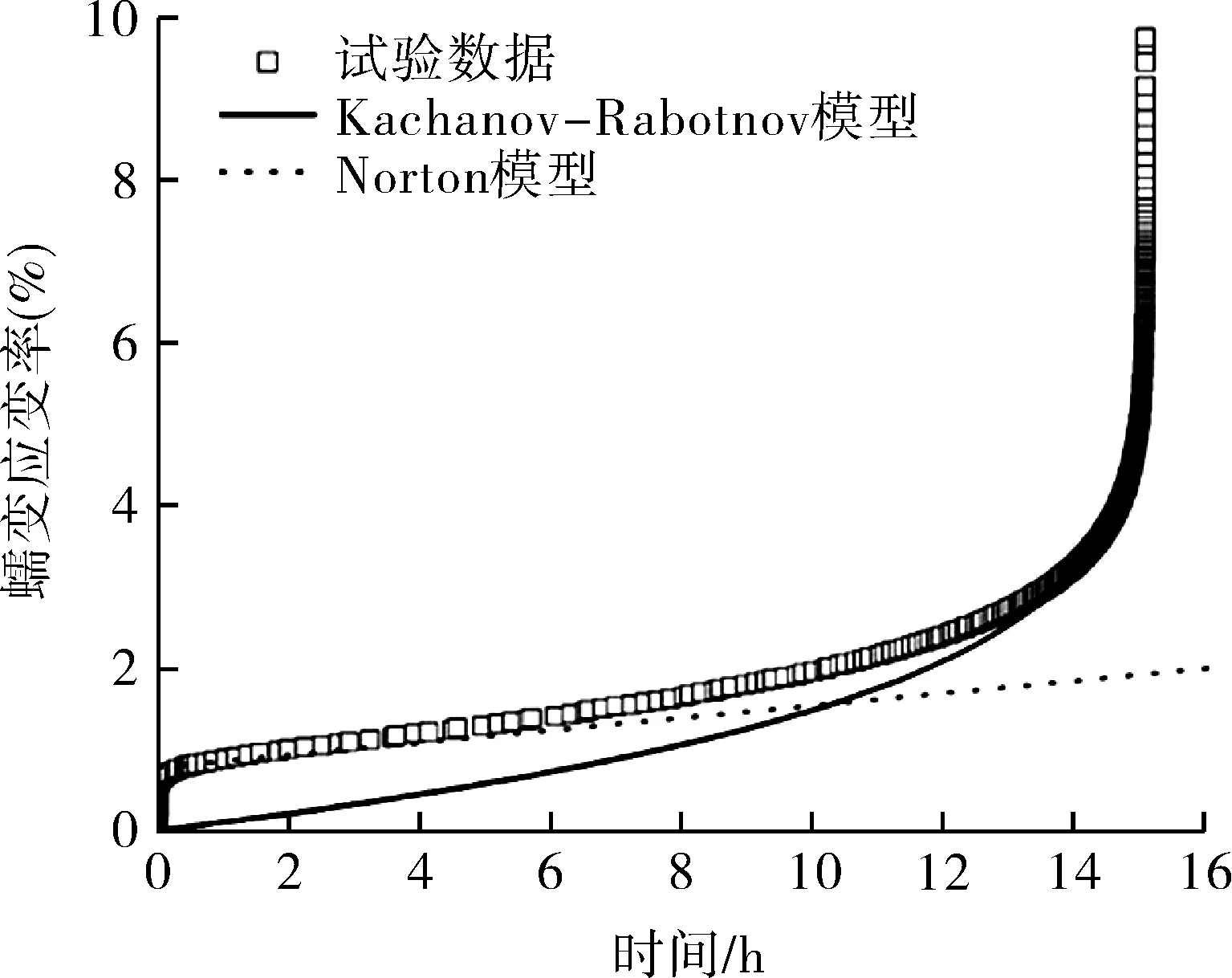
(c)σ=180 MPa

由图8可以看出，Norton模型在表达蠕变过程时，其蠕变变形率与时间呈线性关系，只能描述整个蠕变过程中的蠕变第二阶段，在蠕变第三阶段时则与实际情况相差过大，无法准确表示完整的蠕变过程。Kachanov-Rabotnov模型则可以很好地表述整个蠕变过程，尤其在蠕变第三阶段，Kachanov-Rabotnov模型比Norton模型能够更加准确地描述蠕变过程。因此从蠕变应变的角度出发，Kachanov-Rabotnov模型是最为适合准确体现T91/TP347H材料蠕变特性的。

3.2 各模型下蠕变损伤的分析

基于Norton定理的蠕变损伤表达式：

(23)

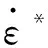
使用Norton蠕变损伤模型能够计算出蠕变第二阶段的损伤，但是无法计算蠕变其他阶段的损伤，并且由于试验存在的各种因素，其数据精度很难保证[35-36]，所以Norton模型不合适预测材料的实际损伤。Kachanov-Rabotnov蠕变损伤模型可用式(9)表示，双参数及三参数的非线性连续损伤力学模型的蠕变损伤则分别通过式(15)和式(19)数值计算获得，其损伤曲线如图9所示。

从对比的结果分析，三种模型预测的断裂时间总体相差不大，但是其临界损伤与损伤轨迹却存在着明显差异。Kachanov-Rabotnov模型在损伤D达到0.3～0.4时便已发生破裂，而非线性连续损伤力学模型则是在损伤D达到1时发生破裂。这是因为Kachanov-Rabotnov模型为解析表达式，无法在数值计算中得到损伤D=1的结果，从蠕变过程来说，蠕变的第三阶段损伤增加得非常快，损伤会在一个极短的时间内从进入第三阶段发展到完全损坏,所以在实际工程中，通常取损伤在0.2～0.4之间的值作为临界损伤。非线性连续损伤力学模型是通过数值计算的方法，从理论出发，当损伤D=1时为临界损伤造成完全损坏，与Kachanov-Rabotnov模型相比，这种模型可以更加完整和广泛地描述损伤过程，而Kachanov-Rabotnov模型则在描述整个损伤过程时存在一定的局限性。

(a)σ=140 MPa

(b)σ=160 MPa

(c)σ=180 MPa

3.3 各模型下预测断裂时间的分析

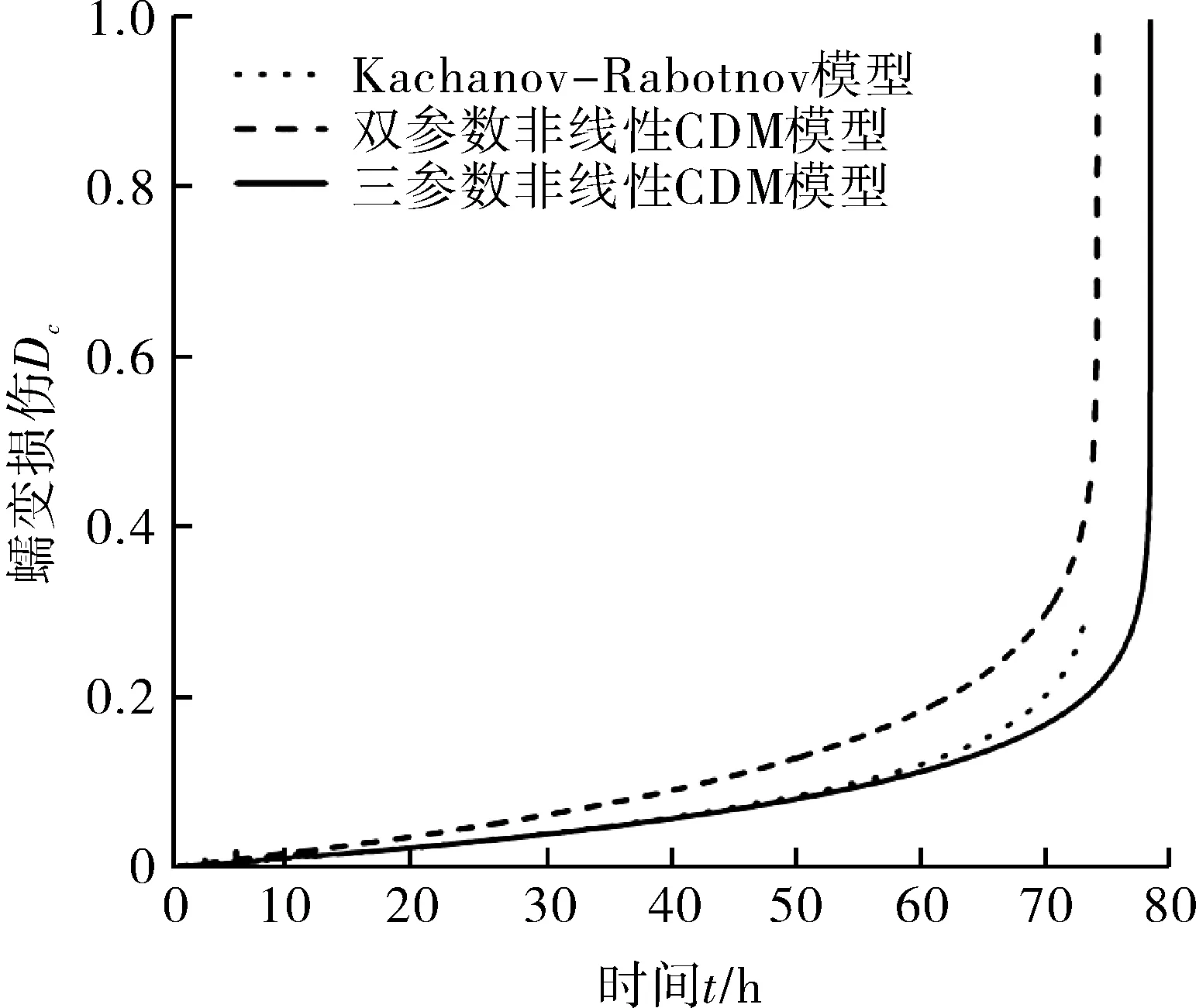
表8 Norton模型、K-R模型和非线性连续损伤力学模型材料断裂时间对比

Norton模型和Kachanov-Rabotnov模型的断裂时间可通过式(4)和式(7)求出，而非线性连续损伤模型则需利用式(15)和式(19)计算其损伤，当损伤D≥1时所对应的时刻便是断裂时间。各模型的断裂时间对比如表8所示。

通过对各模型预测的断裂时间进行对比可看出，与试验数据相比较，Kachanov-Rabotnov模型、双参数非线性连续损伤力学模型和三参数连续损伤力学模型的整体预测结果较为准确，整体误差不大，其中双参数非线性连续损伤力学模型最为精确，而Norton模型的预测结果整体误差偏大。

4 结论

(1)将各种模型下的拟合蠕变应变曲线与试验曲线相比较，可以看出Norton模型只能在蠕变第二阶段与试验曲线相符，在蠕变其他阶段与实际相差较大，Kachanov-Rabotnov模型则较好地描述整个蠕变过程，而非线性连续损伤力学模型无法从蠕变应变角度表述蠕变过程。

(2)从各模型损伤曲线的对比来看,Kachanov-Rabotnov模型的临界损伤在0.3～0.4之间，双参数及三参数的非线性连续损伤力学模型的临界损伤均为1，所以在计算损伤时，Kachanov-Rabotnov模型具有一定的局限性，而非线性连续损伤力学模型可以更加完整地计算整个损伤过程。

(3)将各种模型下的预测断裂寿命与试验数据比较，发现Kachanov-Rabotnov方程、双参数非线性连续损伤力学模型和三参数非线性连续损伤力学模型的预测寿命与试验数据较为接近，其中双参数非线性连续损伤力学模型的预测寿命最为准确，而Norton方程的预测寿命整体偏差较大。