基于双变压器结构的多谐振高频链矩阵整流器的调制策略与建模分析

王汝田，李晓飞，孙 超

(1.东北电力大学电气工程学院，吉林 吉林132012；2.国网吉林省电力有限公司物资公司，吉林 长春130000)

高频链矩阵整流器(HFLMR)是在传统的间接矩阵变换器基础上发展而来的一种新型变换器.有以下优点[1-3]：可以实现单位功率因数，能量双向流动；由于省去了电解电容，无直流储能环节，使得系统结构紧凑，提高了系统功率密度.因而，HFLMR有着极大的研究价值和应用前景.

文献[4-6]中，将HFLMR应用于风力发电中，直接进行高压直流输电，可以进行准确的最大风能跟踪，保证系统安全稳定运行，并且能够对有功和无功功率进行独立解耦控制.文献[7-8]将HFLMR应用于V2G中，给出了充放电的新型控制策略，减少了开关动作次数，提高了系统效率与安全性，实现了能量的双向流动.对于调制策略，文献[9]中作者首先介绍了一种应用于HFLMR的B-C-SVM方法，然后基于传统四步换流提出了一种新的换流方法，省去了额外的检测电流方向的硬件电路，减少了换流步骤，降低了换流成本.

虽然解决了开关管过电压和三相输入电流畸变的问题，但系统的功率密度和传输效率仍有待提高.谐振软开关变换器是一种高效的、低电磁干扰变换器，可以在宽范围内实现软开关，降低开关损耗，也能通过增加开关频率提高系统功率密度和传输效率.将谐振技术应用到高频链矩阵整流系统中是一种创新，目前相关的研究较少.文献[13]为了防止因变压器漏感存在使得矩阵开关出现过电压的现象，在高频变压器原边增加了一个串联LC，通过设计参数形成串联谐振，使得电压过冲现象得到抑制.文献[14]中在直流侧加入一个串联谐振电路，但它只能够实现开关管的软开关启动，关断的时候电流不为零，开关损耗大.上述仅仅是利用了简单的串联谐振，将LLC应用于HFLMR时，虽然也能谐振，但是谐振电流过大，系统得不到稳定的直流输出电压和电流，开关管过电压现象仍然存在.谐振变换器的特性会受到一些特征变量的影响，导致应用范围受限.尤其是电压增益影响最为严重，若电压增益曲线很平缓，将会使得变换器的启动和短路保护变得困难[15-17].多个谐振元件导致变换器具有含谐振零点在内的多个谐振频率点，并且在不同频率点表现出不同的特性.文献[18]提出了一种双向LCLC补偿电容式功率传输(CPT)系统，将其应用于V2G系统，通过补偿结构降低了电容电压应力，保证了输入输出的单位功率因数，但其电流利用率有待提高.文献[19-20]提出了一种新型的多谐振变换器，可以传递基波与3次谐波，提高了电流利用率，实现了软开关，但其仅给出了直流输入场合的实验结果，而现在大部分场合，如电动汽车V2G应用、风力发电和中长距离海上风电电能传输的场合都是三相交流输入，因而不能满足三相输入场合的需求.

针对以上所述，本文结合HFLMR与多谐振技术，提出了一种新型的基于双变压器结构的多谐振高频链矩阵整流器，代替了传统变换器中AC/DC-电解电容-DC/AC两级变换，省去了电解电容，实现了低频交流到正负交变的高频电的直接转换，提高了系统功率密度和传输效率.变压器一次串联二次并联，漏感并入相应谐振电感，降低了变压器自身漏感对变换器性能的影响.与此同时，功率开关管与二极管的通断过程均实现了软开关，降低了开关损耗.控制策略采用B-C-SVM调制策略，可以实现网侧电流正弦化，功率因数单位化.

本文结构如下：第一节介绍基于双变压器的多谐振HFLMR拓扑结构；第二节分析了系统的工作原理，然后对其作了精确建模；第三节介绍针对提出的结构所采用的调制策略；第四节对所提结构与调制策略进行仿真验证；最后在第五节给出结论.

1 系统拓扑结构

本文所提出的基于双变压器结构的多谐振高频链矩阵整流器系统拓扑如图1所示，它由前级3*1矩阵变换器高频整流单元、多谐振单元、后级二极管全桥不控整流单元以及负载组成.

图1 基于双变压器结构的多谐振高频链矩阵整流器拓扑

其中前级3*1矩阵变换器整流单元由六组背靠背连接的IGBT开关组成.多谐振单元中，L1、L2、C1、C2为谐振电感与谐振电容，Lm1、Lm2分别为两个变压器T1、T2的励磁电感，T1、T2为降压型变压器，二次绕组匝数少，漏感对变换器性能影响可忽略不计.图中i1、i2、iC2和iD1分别是流过L1、L2、C2和D1的电流，up与us分别为谐振网络的输入与输出电压.本文所提出的结构代替了传统变换器中AC/DC-电解电容-DC/AC两级变换，省去中间电解电容，减小了系统体积，提高了功率密度，同时具有良好的输入输出波形；实现了工频交流到正负交变的高频电的直接转换；多谐振单元在实现电气隔离的同时提高了系统的传输效率，降低了系统损耗.

2 系统工作原理与建模分析

2.1 系统的工作原理

提多谐振变换器的主要工作波形如图2所示.从图2中可以明确观察到，整个开关周期分为六个间隔.每个间隔对应的运行模态等效电路如图3所示.从图3中GS1-GS6是功率开关管S1-S6的驱动信号.

现今，随着科学技术以及信息技术的快速发展，城市化进程也在不断推进，而土地规划作为一个城市发展的基础，其可以确保城市土地的利用，提高城市交通通畅度，以此来为社会大众营造一个良好的居住环境，进一步保证社会的稳定。而在土地工程管理中引入相应的测绘技术，则可以更好地提高土地测绘数据的准确率。其作为一项先进的新型技术，不仅涉及统计学、线性模式等专业，还包含了信息化技术，而要实现其在土地工程管理中的作用，相应的企业以及单位必须对其技术内容以及实际应用情况进行全面掌握，以此来发挥出其最大效能。

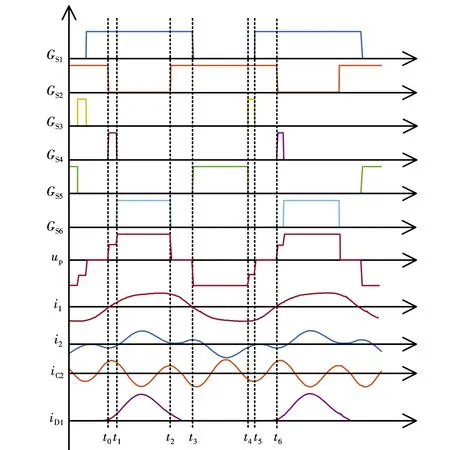
图2 变换器主要工作波形

运行模态1[t0-t1]：此间隔内S1一直导通，在t0时刻电流i1减小到0然后变为正值，开关S2零电流关断，同时S4接收驱动信号.电流由S2换流到S4，实现零电流换流，3*1MC输出正向电压.另外，i1正向流动，i2反向流动，电容C2一直充电，负载由二极管D1、D4导通供电.D1、D4电流从0开始增加，即D1、D4零电流开启.该间隔的等效电路如图3(a)所示.

运行模态2[t1-t2]：此间隔内开关S1一直导通，t1时刻S4关断且S6接收驱动信号导通，电流从S4成功换流到S6，3*1MC输出正向电压.在此期间电流i1与i2正向流动，电容C2在充电结束后开始放电，然后再次充电.负载仍由D1、D4导通供电.图3(b)为此阶段等效电路.

运行模态3[t2-t3]：此间隔内开关S1依旧导通，t2时刻电流由开关S6再次换流到S2，输出电压为0.电流i2正向流动，iC2由正向流动变为负向流动，电容C2开始放电.电流i1正向流动且在t3时刻减小到0，S1以ZCS关断；iD1在t3时刻前减小到0，二极管D1以ZCS关断.对应的等效电路如图3(c)所示.

图3 不同间隔等效电路图

运行模态4[t3-t4]：此阶段为模态2的逆向工作状态，3*1MC输出与模态2相反的负电压，电流方向和电容C2充放电过程与模态2相反，负载电阻由D2、D3导通供电.图3(d)为其等效电路.

运行模态5[t4-t5]：此阶段为模态1的逆向工作状态，不再重复描述，间隔的等效电路如图3(e)所示.

运行模态6[t5-t6]：此间隔内开关S2一直导通，S1在t5时刻接收驱动信号，在此之前S1两端电压已降至为0.由于S1不能瞬间开通，谐振槽电流i1继续反向流动，逐渐减小.S1通过ZVS开通以后，与S2形成直通状态，此时3*1MC输出电压up为0.另外，i2反向流动，iC2由反向变为正向流动，即电容C2放电结束后开始充电.负载由整流二极管D2、D3导通供电.该阶段在t6时刻结束，相应的等效电路如图3(f)所示.

2.2 多谐振单元建模分析

为了获得多谐振单元在某个特定频率下的基本特性，对文中所采用的多谐振单元作了精确建模.在分析谐振网络的基本特性前，对系统做了两点近似处理.其一为忽略内阻，其二为采用等效基波法(FHA)对变换器进行建模，变换器基波等效电路如图4所示.图中Up(s)、Us(s)分别为谐振网络的输入和输出电压；流过电感L1、L2和电容C2的电流分别为I1(s)、I2(s)和IC2(s)；变压器T1、T2流出的二次电流分别为Io1(s)、Io2(s).各个电流的正方向在图中已给出，如图中箭头所示.后级全桥不控整流单元、滤波电容Co以及负载R组成了一个非线性输出单元，根据基波等效法，可将其用一个交流等效电阻Req代替，Req的表达式为

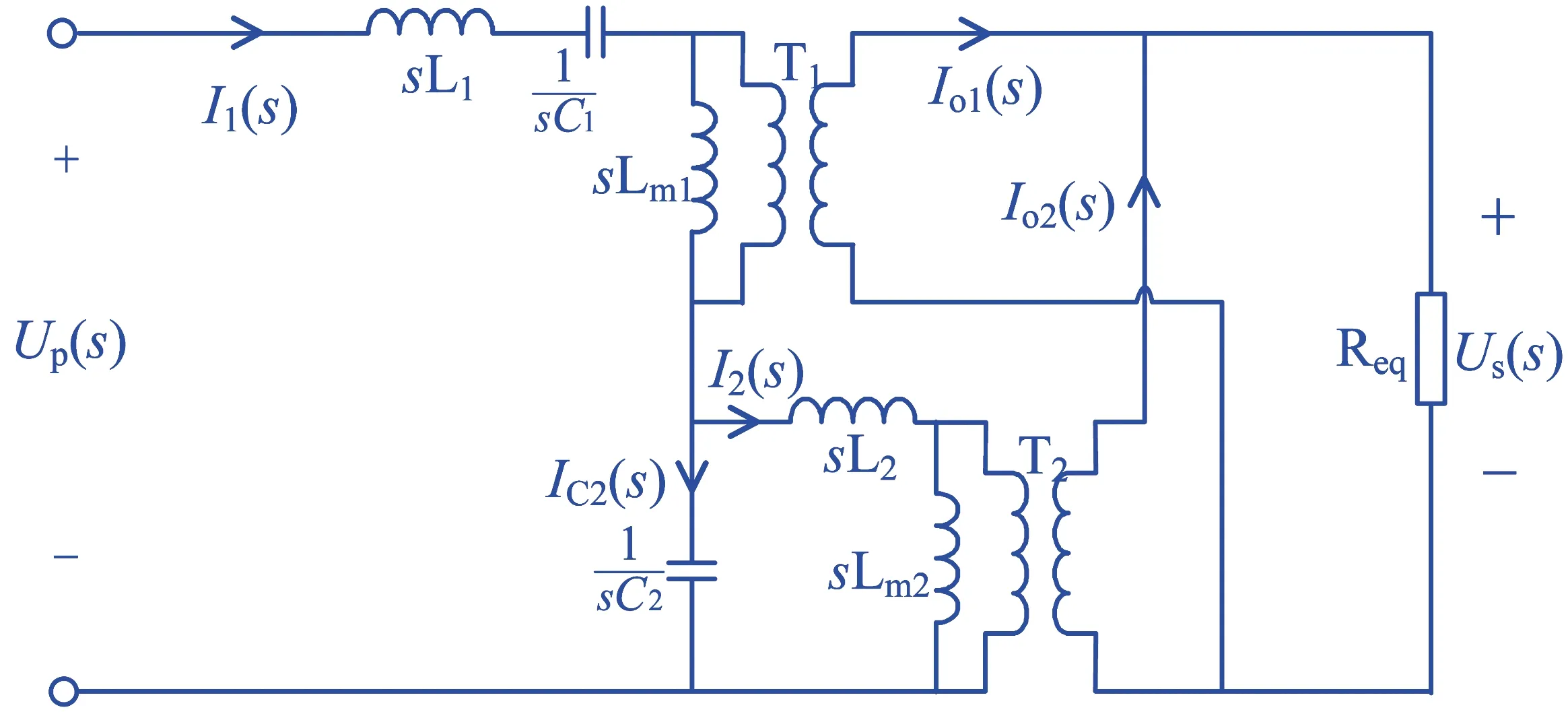
图4 多谐振单元FHA等效电路

(1)

根据图4所示电路，列写相应的KCL/KVL方程，即

(2)

公式中：UT1(s)、UT2(s)分别为变压器T1、T2的一次侧电压.

对变压器参数进行折算，则变压器电压、电流有如下关系

(3)

(4)

此外，谐振网络输出电压Us(s)还可以表示为

Us(s)=Req[Io1(s)+Io2(s)].

(5)

联立公式(2)～公式(5)，可以得到以下两个关系式

(6)

(7)

将上式做以下处理，令

(8)

公式中：As、Bs、Cs均为中间变量，将处理后的公式(6)代入公式(7)，可以得到Us(s)与Up(s)的关系为

(9)

文献[9]给出了3*1矩阵变换器输出的交变高频电压的幅值平均值|Up|与输入相电压幅值|Ui|的关系为

(10)

公式中：m为电流调制度，本文给定为0.8；φ为输入相电压与相电流夹角，要想达到单位功率因数，即相电压与相电流同相位，需保证φ=0.输出整流单元为不控桥式整流，则系统输出电压幅值|Uo|与谐振单元输出电压幅值|Us|关系为

(11)

变换器的电压增益Mgain可用Uo与输入相电压Ui的比值来表示，即Mgain为

(12)

将公式(9)、m=0.8以及s=jω代入公式(12)中，增益Mgain最终可以表示为公式(13)，ω为开关频率fs所对应的角频率，关系为ω=2πfs.Aω，Bω和Cω为中间变量，如公式(14)所示.

(13)

(14)

除此之外，变换器的多谐振单元含有多个谐振频率点.根据Mgain表达式，当其虚部分子为零，即Aω=0时，谐振单元刚好处于谐振点f1和f2处，分母为零时系统处于谐振零点.解虚部分子为零方程可得到谐振点处的频率为

(15)

公式中：aω与bω为中间变量，表达式为

(16)

解虚部分母为零方程可得谐振零点

(17)

根据电压增益Mgain表达式，利用MATLAB软件编写程序，然后绘制出如图5所示的变换器在不同负载下的电压增益曲线.由图5可知，变换器含有3个频率谐振点，分别为f1、f2和f0，与上述理论分析一致.图中可以看出谐振点处的电压增益与负载没有关系，在其他地方则随负载的加重逐渐增大.图5对应的曲线中，变换器在f1附近取得最大值，然后随开关频率的增加，在f1～f2频率段内先下降后上升.当fs大于f2时，Mgain迅速下降，并且在f0点下降为零.增益在f1处取得最大值，在大于f1对应的开关频率区域，变换器可以实现ZVS开通.所以fs应始终保持在此范围内，使得变换器可在较宽范围内实现软开关.本文取电压增益最大时对应的频率，即研究fs为10.2 kHZ时对应的系统特性.

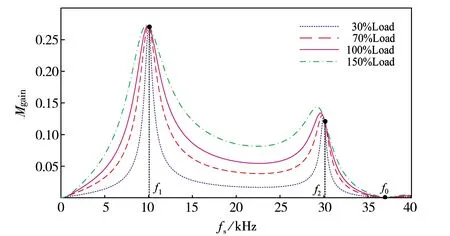
图5 不同负载下的电压增益曲线

3 调制策略

传统整流器的输出直流电压极性不变，HFLMR为了与谐振单元配合，调制方法将会与传统调制有所不同.它由5个矢量来合成参考输入电流：2个用来合成正电流+Im的基本矢量(Im为一个开关周期内电流平均值)、2个与之极性相反的用来合成负电流-Im的基本矢量和零矢量，这样就能使得3*1MC输出一个正负交变的高频电压，满足多谐振单元的工作条件.输出极性有正有负，故将这种合成参考矢量的方法称之为双极性电流空间矢量调制(B-C-SVM).

扇区划分如图6(a)所示，以1扇区为例，参考输入相电流由5个基本矢量(Iab、Iac、Iaa、Ica和Iba)来合成.在前半个周期内，由参考电流相邻的两个基本矢量作用输出正电流，即iout=Im；后半个周期内，由与前半个周期极性相反的基本矢量作用时输出负电流iout=-Im.除了这两对基本矢量外，还需在有效矢量中插入零矢量，使得输出电流的平均值在每个周期内为常数.

假设在前半个周期，输入参考电流矢量由相邻的2个非零矢量Iα1和Iβ1以及对应的零矢量I0合成.此时3*1MR输出电流为Im.基本作用矢量如图6(a)所示，Iα1、Iβ1以及I0对应的占空比计算公式dα1、dβ1和d01表示为

(18)

公式中：tα1、tβ1、t01分别为空间矢量Iα1、Iβ1、I0的作用时间；m为电流调制度，Iim为输入相电流幅值，且有0≤m=Iim/Im≤1；角θr为输入参考相电流矢量Ir与非零矢量Iα1之间的夹角，如图6(b)所示.

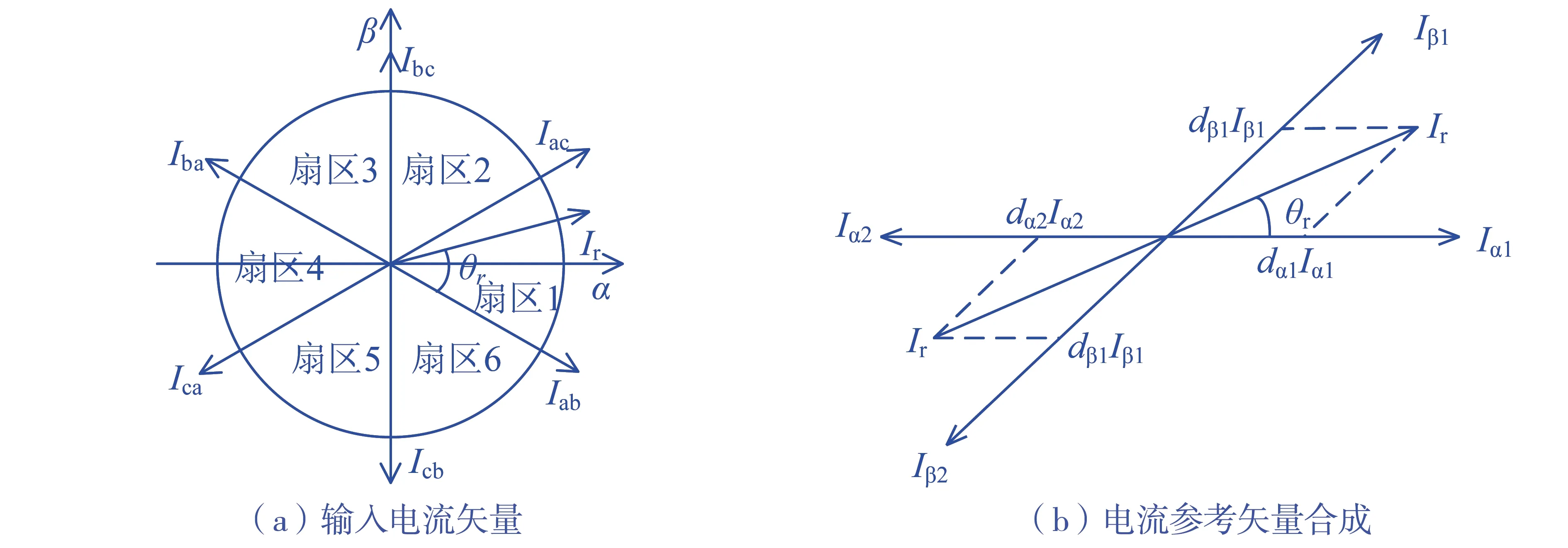
图6 输入相电流空间矢量与合成

后半个周期使用与Iα1、Iβ1极性相反的Iα2、Iβ22个有效矢量以及零矢量来合成参考矢量，合成方法与上文所提基本一致，如图6所示.此时3*1高频链整流器输出的电流在前后两半个周期内极性相反.通过B-C-SVM调制后MR输出电压以及开关相关动作如图7所示.由公式(18)可以看出占空比表达式仅和θr和m有关，即只需这2个参数恒定，就可以保证前后两半个周期内矢量的占空比相同，即dα2=dα1、dβ2=dβ1、d02=d01.通过以上参考矢量合成方法，就可以保证3*1MC能给与多谐振单元配合，输出正负交变的高频电.

图7 MR输出电压顺序与开关驱动信号

4 仿真实验分析

为了验证文中所提系统的有效性和可行性，基于Matlab/Simulink和S-function建立了系统的仿真模型.综合考虑各方面因素，仿真模型参数如表1所示.电网电压为220 V三相对称电压，fs为转换器开关频率.

表1 主要实验参数

网侧滤波后A相输入电压ua与电流ia波形如图8所示，图8中电流为实际值的5倍，由图8可见，电流能够跟随电压变化，电流电压基本同频同相，实现了单位功率因数的目的.

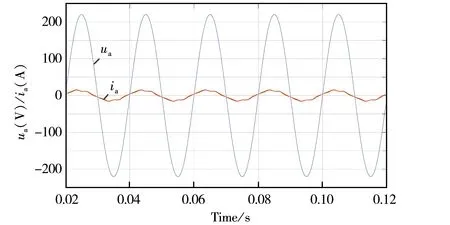
图8 网侧A相输入电压、电流波形

谐振回路输入和输出的电压电流波形如图9所示，图9(a)是谐振回路输入稳态电压up与电流i1，也是3*1MC输出稳态电压电流波形，图中电流为实际值的10倍.图9(b)是谐振回路输出稳态电压us与电流is，也是副边控整流桥的稳态输入电压电流图.从图中可见，变换器实现了工频交流电到正负交变的高频电的直接转换.同时，电流与电压频率和相位变化大体一致，表明变换器具有高功率因数.

图9 谐振回路输入输出波形

高频变压器原边电压电流仿真图如图10所示，图9(a)是变压器T1的原边电压uT1与电流iT1，图中电流为实际仿真值的5倍.图9(b)是变压器T2的一次侧电压uT2与电流iT2，图中电流为实际仿真值的3倍.由图可见，在变压器原边电流为零时电压开始出现极性变换，也就是说3*1高频链矩阵整流器功率开关管通断时输出为电压为零，实现了零电流换流.

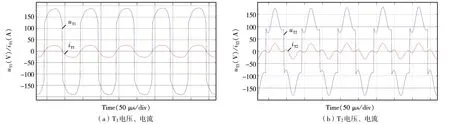
图10 变压器一次侧电压电流波形

功率开关管和二极管的电压电流波形如图11所示，图11(a)是功率开关管S1的电压uS1与电流iS1，电流为实际电流的10倍，图11(b)是二极管D1的电压uD1与电流iD1.由图11可知，电压的转变即开关的通断总是在电流为零的时候，开通时电压先降到零然后电流再缓慢上升到通态值，关断时电流缓慢降到零然后电压上升到通态值，开通关断过程无电压电流重叠，实现了软开关操作，极大地降低了开关损耗.

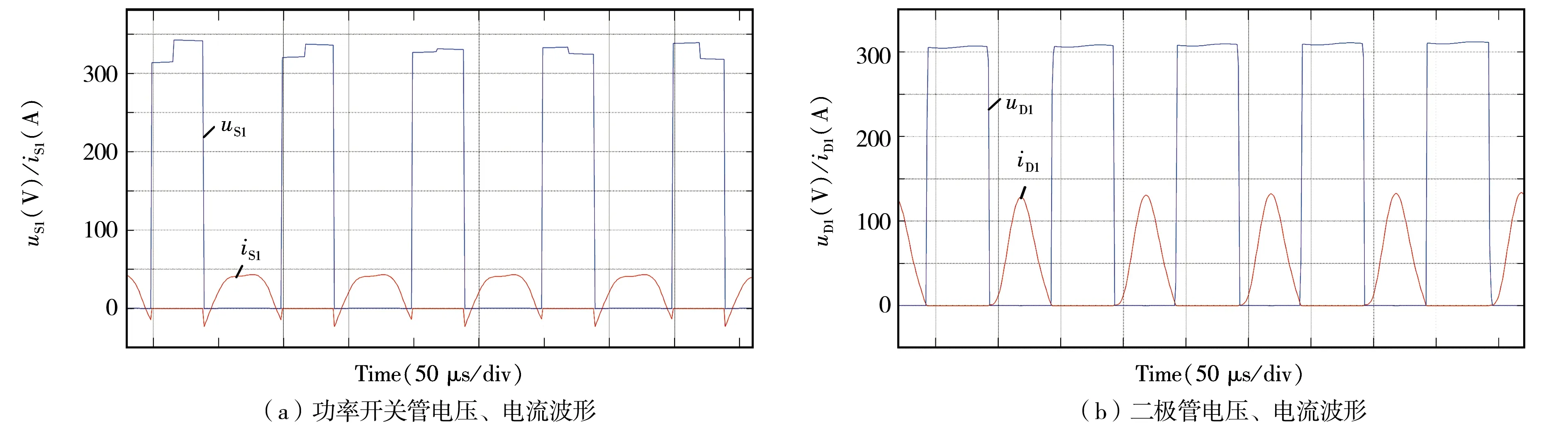
图11 功率开关管和二极管的电压电流波形

取自稳定后的负载输出电压波形如图12所示，由图12可知，输出电压在达到60.5 V左右后基本保持稳定状态，实现了输出电压稳定的目的.若想取得其他期望的稳定电压值，可以在确定增益后调节多谐振单元中电感与电容的大小来实现.

图12 负载的输出电压

5 结 论

文中提出了一种基于双变压器结构的多谐振HFLMR，针对此结构对双极性电流空间矢量调制方法进行优化，使3*1MR能输出正负交变的高频电，网侧输入电流正弦化，功率因数单位化.通过分析变换器的工作波形与运行模态，以及对多谐振单元的精确建模，得出了谐振参数与谐振频率点之间的关系.高频矩阵整流与多谐振相结合，使得变换器功率开关管与二极管都能实现软导通与关断，降低了变换器的开关损耗.最后，通过仿真模型，验证了所提系统的有效性和可行性.