基于动态加权集成学习的遥测数据预测方法

梅玉航,贾海艳

(中国人民解放军92941部队，辽宁 葫芦岛 125000)

0 引言

遥测数据主要用于获取飞行器上各子系统的运行状态监测数据，通过分析遥测数据以监测各子系统功能正常与否并对其进行安全控制[1]。遥测数据本质是多维时间序列，同时遥测数据易受测量设备、空间环境和运行状态等影响产生不明显的数据漂移变化，其表现可能是数据的突变形式，也有可能是缓慢的线性变化等，变化趋势不易判断，对其进行数据分析的主要问题之一是能进行高精度的预测，从而判定其监测的子系统状态是否正常。

目前用于时间序列预测的方法有两类:一类为数学和统计方法，如线性回归，ARIMA方法和指数平滑等[2-3]；另一类基于机器学习方法，如支持向量机回归[4]，随机森林和神经网络等[5-6]。对某种模式时间序列的预测都存在特定对应的方法，但在时间序列存在数据漂移的情况下，随着时间的推移，这些方法预测的精度会不断降低。集成学习的优势在于即使一些基学习模型不能准确预测时间序列模式的变化，但另一些基学习模型能实现精确预测，通过对各基学习模型预测输出的加权求和从而实现预测误差相互抵消，使总体的预测精度得到补偿。因此通过集成多样性的基学习器能解决传统预测方法随时间性能下降的问题[7]。

在遥测数据分析处理过程中不可避免伴随着噪声，而噪声源通常不易确定，因此人工智能神经网络方法更适合对遥测数据的预测。神经网络借助有监督学习方法能建立输入变量与输出变量间复杂的函数关系[8]，目前广泛用于解决预测问题，其预测精度和效率取决于神经网络的结构和训练方法[9]。另外，神经网络对于遥测数据预测还具有一些特殊的优势：神经网络具有自学习能力，有多个可供选择的转换函数和神经网络结构；通过多层神经网络的隐层神经元的非线性特性可实现非线性映射功能；高度的并行机制可提高预测的实时性。凭借以上优点，神经网络算法可实现具有复杂算法的数据预测。但是，传统的神经网络方法在确定复杂神经网络的参数时需要占用一定时间和资源，因此针对多变量时间序列预测问题需要开发能自动确定网络参数和结构的工具，以找到参数最优解。

考虑到如前述使用单一预测模型存在不稳定性，而集成算法模型能有效解决模型的泛化性和可信度[10-11]，因此提出一种基于动态加权神经网络(NNRW)集成学习方法[12]，通过集成多个较简单神经网络来替换单一复杂的神经网络，从而减少预测模型建立的时间和复杂性，保证遥测数据预测的实时性。选择神经网络作为基学习器，根据各基学习器目前和过去的性能，动态调整输出权值，实现对遥测数据的预测，并提高预测的总体精度。

1 集成预测原理

集成预测通过集成学习方法获取数据预测模型，该方法的主要原则是利用基模型的多样性，通过对不同基模型输出的适当联合进而获取到相比于其中最优的单个基模型更精确的结果。集成学习过程具体分为3个阶段：集成产生，集成修剪和集成整合。在集成产生阶段，训练完成一组具有多样性的预测基模型。在集成修剪阶段，实现消除基模型集合的冗余，剔除高误差模型，从而提高最终预测的总体精度。最后在整合阶段，利用各基模型计算结果的线性联合实现对各基模型预测结果的整合，以获取最优的预测结果。

为解决飞行器上多个子系统遥测数据预测问题，针对各子系统配置相应的神经网络集成学习器，遥测数据经预处理后，各子系统相关的遥测数据集分别输入对应训练完成的集成学习器，并输出下一时刻的状态参数预测值。其工作原理如图1所示。

图1 神经网络集成预测工作原理图

子系统识别ID通过通信模块传递到控制器，控制器可控制不同子系统对应的遥测数据预处理数据集依次输入相应的神经网络集成学习器，并将集成学习器预测结果传回控制器进行输出，当控制器发现某个集成学习器预测性能下降时，向递增学习模块发出学习信号，该递增学习模块进行训练初始化，完成训练数据集准备和新的神经网络的训练，训练完成后对集成学习器中性能变差的神经网络基学习器进行替换。

2 神经网络(NNRW)集成学习器

飞行器遥测数据本质是一个多维时间序列，该时间序列为按照严格的采样间隔获取的数据集，而时间序列预测是利用已知数据Yt-n…Yt-3,Yt-2,Yt-1,Yt, 预测得到Yt+1[10]。其中：Yt+1为集成神经网络预测得到的目标值；Yt为已知的观测值；t为时间轴上的序列号。

2.1 集成学习器原理

基于神经网络的预测，要求具有较高的预测精度以及计算效率，可以满足遥测数据处理的要求。考虑到单一神经网络存在不稳定性，而集成学习方通过联合多个同质或异质神经网络进行预测，不仅可实现预测模型的泛化性能，而且预测精度可高于单一最优神经网络，神经网络集成学习器由多个同质神经网络构成，这样可获得稳定的预测输出，极大减少神经网络的设计参数数量，简化了参数选择和优化过程，提高了集成学习器的效率。

集成学习器原理如图2所示。

图2 神经网络集成学习器

一个神经网络集成学习器包含一组神经网络基学习器，其中的每个神经网络基学习器都独立对输入的遥测数据进行预测，神经网络基学习器的结构为单隐藏层的前向反馈多层感知机，为简化集成学习器结构和提高预测性能，将各神经网络基学习器输出的加权和作为集成学习器的输出预测值。该种方法可保证预测的精度优于其中最优神经网络的预测精度并能在数据存在漂移及扰动时对预测结果进行平滑处理。

2.2 多层感知机神经网络

神经网络基学习器为多层感知机神经网络(multilayer perceptron)结构，该结构设计具有一个输入层，一个隐藏层和一个输出层结构。

其功能函数如式(1)所示：

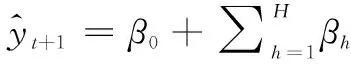
(1)

其中:I表示神经网络输入pi的数量；H为神经网络隐藏层节点数量；g(·)为非线性激活函数，这里为双曲正切函数。

β=[β1,...βH]为输出层权值；γ=[γ11,...γHI]为隐藏层权值；β0、γ0i为单个神经元的偏置。

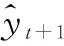
由于基学习器中隐层神经元的数量对预测性能起关键作用，为获得隐层节点数量的最优值，以最小均方误差(MSE)为判定标准，采用搜索方法获取。定义隐藏层神经元数量的搜索间隔[3，31]。训练位于间隔内的10个具有该隐藏层数量的神经网络，评估集成神经网络的精度，之后转换到该间隔内其他值，直至数量间隔搜索完成。选择具有最小MSE的集成神经网络，其隐藏层数量为最优。

2.3 神经网络训练算法

由于反向传播训练算法通常收敛速度较慢，选择Levenberg-Marquard算法，该算法适合于性能指标为均方误差(MSE)的神经网络训练。由于该方法不需要计算正定矩阵，其正定矩阵可近似为：

H=JTJ

(2)

梯度为：

g=JTe

(3)

其中：J为Jacobian矩阵，包含网络误差对权值的一阶导，e为网络误差向量。Jacobian矩阵可通过标准化的反向传播算法求取的，降低了计算正定矩阵的复杂性。

如果权值和偏差更新等于δ:

δ=ΔWm(k)+Δbm(k)

(4)

因此Levenberg-Marquard算法近似如下函数:

(JTJ+μI)δ=Jte

(5)

其中:J为神经网络的Jacobian矩阵；μ为阻尼因子；δ为权值更新向量；e为误差向量。

每次成功的迭代都会减小μ值，当迭代中性能函数增大时，μ值增加，这样性能函数在每次迭代循环中总是递减，当性能指标达到时算法收敛。

2.4 动态加权算法

以往集成学习的加权算法是一种各基学习器输出权值为静态和固定值的方法，其权值确定方法如式(6)所示:

(6)

其中：msei为第i个神经网络在验证数据集上的测量均方差。

动态加权方法中每个神经网络基模型的权值根据其过去和现在的预测性能改变，该方法具有优于静态加权集成方法的性能。神经网络集成学习器输出为：

(7)

∀k=1,2,…,N

wk,i为第i个模型的在数据k上的权值，取决于第i个模型和时间索引k。设权值为非负且无偏。

每个基模型的过去性能由样本内验证数据集评估，目前性能由样本外预测评估，通过利用预测误差作为评估标准，对基模型输出权值进行增减。具体算法如下：

β：缩减因子，

θ：神经网络基学习器移除时权值对应的门限值

p:神经网络基学习器替换周期

Λ,λ{1,..,c}：总体和局部预测；

m：集成学习器中神经网络基学习器数量

ε1,...m：预测误差

步骤：

(1)训练获得神经网络基学习器

(2)w1,...m←1/m

(3)fori=1,…,m do

(4)Λ=0

(5)for j←1,…,m do

(6)λ←predict(ej,xi)

(7)εj←MAPE(λ,yi)

(8)Λ←Λ+λ*wj

(9)w←lowerweights(w,ε)

(10) ifI mod p=0 then

(11) for j←1,..,m do

(12) ifwj<θ then

(13)e,w←replacewithnewNN()

(14)归一化w

(15)输出Λ

该算法初始训练并创建一组m个多层感知机神经网络作为基学习器，各基学习器具有相等的权值。迭代开始获取训练样本的预测值，这些局部预测值与权值之积与全局预测值Λ进行累加，计算每个基学习器的预测误差，如式(8)所示，以向量形式保存：

(8)

其中:n为样本数量，At为实际值，Ft为预测值。

算法中通过转换函数实现权值动态权值更新，如式(9)所示，对预测性能最差的基学习器权值分配缩减因子β，而对其它基学习器逐渐增加乘子，直到理论最大值1。

(9)

3 实验验证及分析

遥测数据集是由飞行器上各子系统功能传感器产生输出的一组连续监测数据，表征了各子系统的特定功能和状态。各子系统的监测参数依赖于飞行器的运行状态，同时各监测参数间具有一定的相关性。针对遥测数据预测问题，利用多层感知机神经网络具有的数据预测特性，采用动态加权算法集成多个感知机神经网络做为基学习器，通过对各基学习器预测结果的加权计算，实现对各基学习器的预测结果进行一种优化平均运算，以减小计算结果的分散性，满足遥测数据预测精度要求。飞行器遥测数据有距离、速度、俯仰角以及内部各传感器采集的数据，为验证集成学习预测的性能，选用飞行器某气体单元子系统内压力参数的遥测数据作为实验样本集进行集成学习算法的验证，并对集成学习模型的性能进行评估。

3.1 数据处理

由于多层感知机神经网络为有监督学习，为了保证训练的神经网路预测性能最优，需要保证一定规模的数据进行训练，首先需要产生具有输入向量，输出向量的训练数据集。为此采用滑动窗口技术获取训练数据集，具体过程为从遥测数据的时间序列中抽取对应窗口的片段作为输入向量，输出值的期望值为对应该窗口的下一顺序观测值。通过在遥测数据上逐个数据滑动窗口，随着时间从一个位置变换到下一位置，串行连接每个片段构成训练数据集。

将获取的数据样本集划分70%为训练集，15%为验证集，15%为测试集三部分，训练集和验证集用于训练，估计和搜索最优神经网络结构，最后，使用测试集评估所获得神经网络的预测性能。

多层感知机神经网络结构为包含两个输入的一个输入层，具有15个神经元节点的隐藏层和一个输出层。

3.2 动态加权算法评估

遥测数据集首先需要进行一定的预处理，包括去除噪声，对数据进行归一化处理。在集成学习预测方法中，神经网络基学习器的性能对最终的预测性能起着决定性作用，因此要求对神经网络基学习器进行最优化，最优化参数包括隐层节点数量、隐层输出权值。动态加权集成学习预测算法实际的预测效果如图3所示。

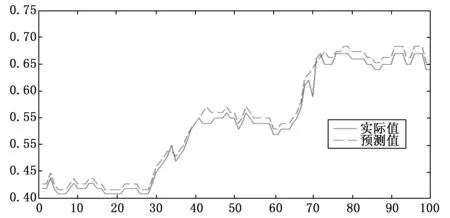
图3 实际数据和预测

为实现动态加权集成算法的性能评估，将其与静态加权算法进行比较，两种算法具有完全相同的网络结构参数和基学习器数量，静态加权算法只对各基学习器预测结果进行简单的平均运算，将两种算法输出结果的MAPE指标作为算法性能的判断标准。其性能比较结果如图4所示。

图4 动态和静态加权算法性能比较

结果表明集成学习器中合理的神经网络基学习器数量为5～9个，包含更多数量的神经网络基学习器对集成学习器预测精度提升效果有限，而且增加了计算复杂性。同时MAPE指标也表明推荐的动态加权方法同静态加权方法相比具有更小的预测误差。

4 结束语

针对飞行器遥测数据预测中要求具有实时性和高精度的需求，提出基于多层感知机神经网络的动态加权集成学习方法，该方法通过集成多个多层感知机神经网络作为预测基学习模型降低了预测模型的复杂度，提高了预测模型的实时性，实现了更加精确的预测，给出了多层感知机神经网络的设计、优化方法和动态加权算法的过程。对于遥测数据存在异常漂移情况，通过给出的动态加权算法，能识别优秀的神经网络基学习器，增加其输出权值，对性能差的神经网络基学习器减弱其对预测输出的影响，甚至对其进行更换，从而提升预测结果的精度。

采用飞行器某子系统内的遥测数据对集成学习方法性能进行了验证，确定了感知机网络隐藏层的最优节点数和神经网络基学习器数量的最优值，通过与静态加权集成学习方法的比较，结果表明提出的动态加权集成方法预测精度更高。该集成学习预测方法也取决于神经网络基学习器的参数选取，通过对隐藏层节点数量和学习速度进行最优化设计，可以保证最终的集成结果也是预测最优值。