基于IGWO-BP的SCR脱硝效率软测量模型

章文涛,张东平

(1.南京工程学院 电力工程学院，南京 211167； 2.南京工程学院 环境工程学院，南京 211167)

0 引言

随着我国经济高速发展，工业用电需求日益增长。现阶段煤炭仍是我国的主体能源[1]，而火力发电过程中排放的烟气含有多种有害物质，因此针对燃煤电厂排放物进行的脱硫、脱硝等措施尤为重要。选择性催化还原(SCR)方法作为燃煤电厂烟气脱硝的主流选择，通过催化剂催化，烟气中氮氧化物(NOx)与还原剂反应后产生氮气与水，可高效控制排放烟气中氮氧化物含量[2-3]。火电厂对SCR系统脱硝效果有实时监测的客观需求的同时，由于SCR系统脱硝效率影响因素较多且相互间存在强耦合性与非线性关系，使得难以通过反应机理建立有效模型对其进行准确的预测。

随着机器学习的研究与应用，智能算法在火电厂SCR脱硝系统中应用广泛[4]。工程上有利用长短时记忆循环网络对脱硝效率进行预测，如温鑫等[5]将深度循环神经网络与LSTM结合，把时间因素纳入考虑，构建出拟合效果好的预测模型。支持向量机在该领域也有所应用[6-7]，文献[8]利用PSO算法对双支持向量机的参数进行寻优，从而构建PSO-TWSVM模型，在提高预测精度的的同时降低计算时间。杨碧源[9]等人针对蜂窝型催化剂，利用BP网络建立SCR脱硝预测模型。

针对BP算法存在过拟合、易陷入局部最优解等问题[10-11]，本文提出一种基于改进GWO-BP的SCR脱硝系统效率预测模型对大唐洛河发电厂6号机组脱硝装置进行效率预测。该算法主要创新点在于：在传统BP算法基础上，通过主成分分析进行降维,调整灰狼算法中的收敛因子与指导权重，再于算法前期加入随机引导狼进行改进，而后用改进后的灰狼算法优化BP初始网络结构，避免算法陷入“局部最优陷阱”，提高该算法非线性学习能力。

1 IGWO-BP算法结构设计

1.1 BP神经网络

BP神经网络[12]是一种多层前馈神经网络，其通过输入层、隐含层及输出层的拓扑结构进行信号的正向传播与误差逆向传播，在训练过程中使用最速下降法调整网络的权值与阈值，从而使输出结果逐渐接近样本期望值。BP神经网络作为应用最为广泛的模型之一，具有较强的非线性映射能力、自学习与自适应能力。但同时也存在易陷入“局部最小陷阱”等缺点。

1.2 灰狼优化算法

灰狼优化算法(GWO,grey wolf optimizer)由Mirjalili等人[13]于2014年提出，它受启发于自然界灰狼捕食，模拟灰狼族群的社会等级制度与捕食策略，具有优异的全局搜索能力与收敛性能，也可以与其他算法结合进行优化[14]。

灰狼算法的基础是将种群按严格等级制度进行排序(见图1)，其中上三层分别为α层、β层与δ层，底层为ω层，分别对应自然界灰狼族群中的头狼、副手、小头目与底层灰狼。在寻优过程中，头狼始终是最接近猎物的，低级狼群的行动受到高级狼群的指引，随着算法不断迭代狼群位置也不断更新，直至狼群找到最优解，寻优结束。

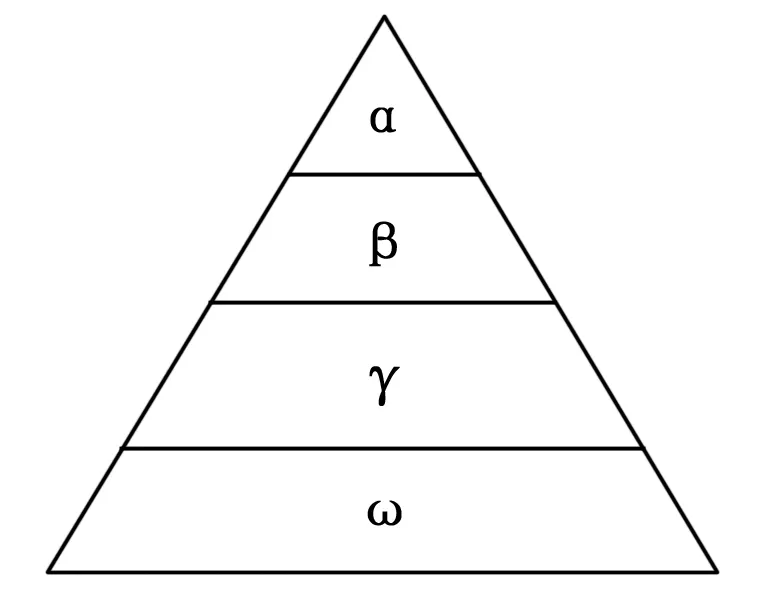
图1 灰狼算法等级制度

1)包围猎物。灰狼算法寻优过程首先需要对最优解进行包围，公式如下：

(1)

(2)

(3)

(4)

a=2-t/tmax

(5)

2)跟踪与猎杀猎物。在寻找潜在最优解的过程中，β与δ在α的引导下对猎物进行包围，在优化过程中模拟自然界狼群捕猎行为，先假设α、β与δ更了解猎物所在位置，并在寻优过程中利用最佳的3个解引导灰狼ω进行位置更新。引导过程如式(6)～(8)所示:

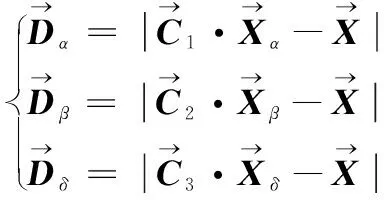
(6)

(7)

(8)

1.3 改进GWO算法

灰狼算法种群位置更新依赖于α狼、β狼与δ狼的引导，若初始位置不理想，容易陷入局部最优陷阱，在算法后期搜索能力变弱，导致最终结果早熟[16]。为解决这一问题，本文首先调整灰狼算法中的收敛因子与指导权重，再于算法前期加入随机引导狼，以达到扩大搜索范围，提升搜索效率的目的。

1.3.1 GWO算法收敛系数调整

(9)

式中，k为根据迭代次数设置的非线性调整参数，t为当前迭代次数，T为最高迭代次数。

1.3.2 优化指导权重

传统灰狼算法中，考虑到α狼、β狼与δ狼本身适应值间存在差异的实际情况，而3者在位置更新中对于ω狼的指导权重完全相同，这不能很好地表现实际中狼群搜寻猎物的情况。因此需要进行权重优化。改进后权重应有助于适应值更高的狼对于狼群有更好的指导权，从而增加狼群逼近最优解的速率。

本文使用一种基于适应度比值的指导权重，表达式如下：

(10)

(11)

(12)

X(t+1)=X1·W1+X2·W2+X3·W3

(13)

式中,W1、W2、W3分别为α狼、β狼与δ狼对于指导ω狼前进所占权重，fα、fβ、fδ分别为前三头狼的适应值。

1.3.3 随机引导狼

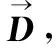
图2 IGWO算法示意图

位置更新公式如下：

(14)

(15)

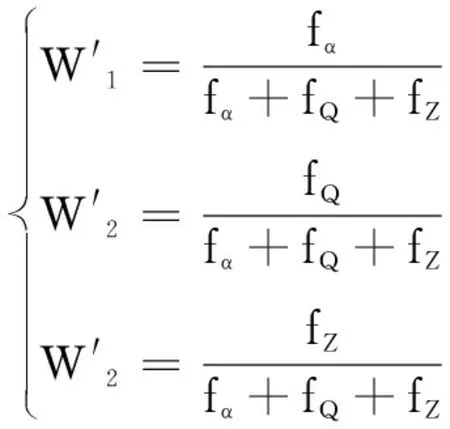
(16)

(17)

利用Ackley函数对改进灰狼算法进行测试，发现IGWO算法在第48代收敛于3.98×10-15，而传统的GWO算法于第412代才收敛于2.12×10-13。由此可见，改进后的灰狼算法具有更高的精度与收敛速度。

1.4 IGWO-BP神经网络的构建

BP网络信号在层与层之间前向传递，误差通过函数反向传递。为了获得更好的预测效果，IGWO-BP网络需在上述结构基础上引入改进灰狼算法，BP网络原本随机产生的初始权值与阈值易使算法早熟，而IGWO算法的加入可以在保留BP神经网络自学习能力强等优点的前提下，对BP网络的初始权值与阈值进行优化，使得算法有更好的全局寻优能力。

IGWO-BP网络建模流程如图3所示。

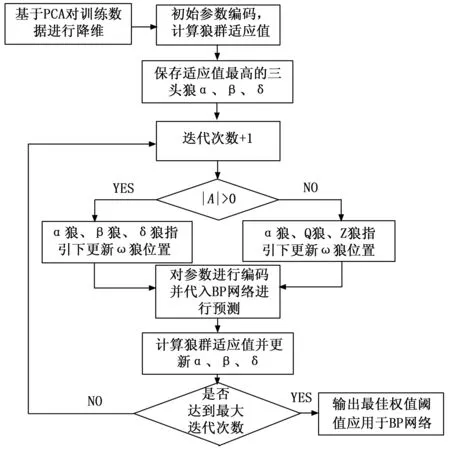
图3 IGWO-BP网络建模流程

2 模型预测实例及分析

2.1 输入变量的选择

图4为传统火电机组SCR烟气脱硝系统，电厂SCR系统一般由氨注入系统、SCR反应系统及氨储存处理系统组成[18]。其主要工作流程为：将原先储存于氨罐中的液态氨(还原剂)通过蒸发器气化后注入SCR系统，经由氨缓冲槽与管道输入锅炉区，与空气混合后喷入烟气中与NOx进行反应。SCR系统参数庞杂，合理且完善的指标选择既是进行脱硝效率预测的前提，也是保证预测结果准确有效的关键。

图4 SCR系统示意图

本模型的唯一输出变量为SCR系统的脱硝效率，通过SCR工作机理分析及燃煤电厂现实运行与监测状况对输入变量进行选择如下。

1)机组负荷率；给煤率与机组负荷率正相关，随着给煤率增大，燃烧室内烟气温度随之提高，生成的氮氧化物也相应增加[19]。

2)尿素溶液流量；作为还原剂，尿素溶液流量对于整个SCR系统脱硝效率影响起关键作用。

3)反应器入口温度；炉内温度越高，反应器入口温度越高，NOx排放量也越大。另一方面，烟气温度对于催化剂活性存在影响，过低的烟气温度会降低脱硝效率，而温度过高也可能会使催化剂产生烧结现象[20]。

4)锅炉总风量与锅炉总煤量；总风量与总煤量代表了锅炉送煤效率。

5)反应器入口Nox浓度；入口氮氧化物浓度越高，对SCR系统脱硝带来的压力越大；

6)反应器催化剂床层压力；反应器内部压力影响系统内反应速率，同时脱硝系统压力损失与催化剂抗腐蚀与抗磨损性能有关。

2.2 基于主成分分析的数据预处理

模型基础数据来源于2020年大唐洛河发电厂6号机组脱硝运行数据参数，采样时间为10月15日至11月1日，采样间隔为5分钟，共4 468组数据。在本次IGWO-BP神经网络预测模型中，采用交叉验证法进行模型训练与检验，具体实施方法为随机取其中4 368组数据进行模型训练，取剩余100组数据进行模型检验。

在基础数据中，包含了机组负荷率X1，尿素溶液流量X2，A、B、C侧反应器入口压力X3、X4、X5，A、B、C侧反应器入口温度X6、X7、X8，上、中、下催化剂床层压力X9、X10、X11，锅炉总风量X12，锅炉总煤量X13，共13项指标。由于各参数量值存在差异，首先需要对脱硫系统参数进行预处理。其公式如下：

(18)

由于原始数据中13个指标之间具有较强的耦合性，且较多的变量不仅会影响灰狼算法与BP神经网络算法的训练成本。为了降低不同变量间的相关性并减少输入变量，使最终的输入参数为互不相关的独立变量，本文对数据进行预处理后，采用主成分分析法(PCA)，对13个脱硝系统参数进行降维处理，得到参数如表1所示。

表1 主成分特征值及贡献率

由表1可知，前6个主成分理论上就占据原先13个指标百分之95以上的信息量，能较好地代表原始元素。故提取前6个由脱硝效率影响因素组成的主成分作为神经网络的输入元素，其特征向量如表2所示。

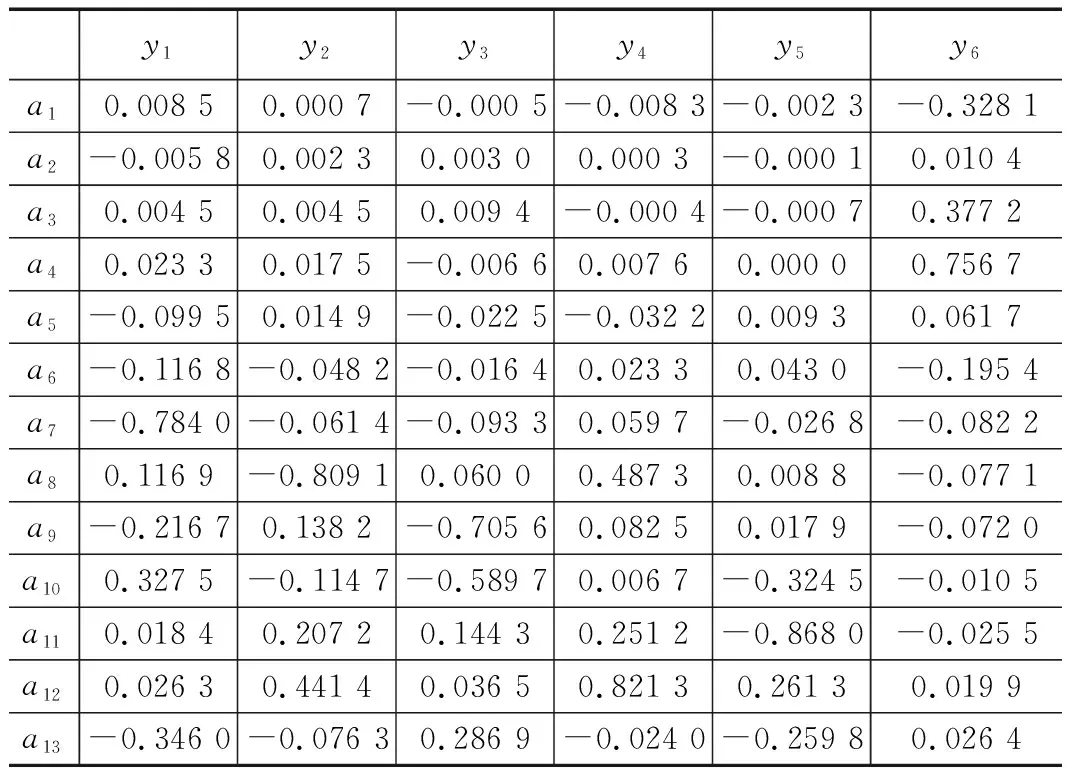
表2 主成分对应的特征向量

表2中,y1,y2,y3,y4,y5,y6代表在PCA处理后得到的6个主成分，每列a1，a2，…，a13为所对应yi的特征向量，代表13个原始变量X1，X2，…，X13在该主成分中所占的比重。

每个新变量yi是由原始13个参数线性组合而成，系数为对应特征向量值。如表2所示，第1个主成分主要反映了B侧反应器入口温度和锅炉总煤量，第2个主成分主要反映了C侧反应器入口温度和锅炉总风量，第3个主成分主要代表了上催化剂床层压力与中催化剂床层压力，第4个主成分主要代表了C侧反应器入口温度与锅炉总风量，第5个主成分主要代表了中下两层催化剂床层压力，第6个主成分主要代表了A、B两侧反应器入口压力。

所以，通过PCA降维处理后的6个主成分既可以较为全面反映原始数据的信息，又消除了数据间的相关性，还通过减少参数种类节约后续网络训练成本。

2.3 脱硝效率预测结果分析

在本模型实际训练的中，将前文提取的6个主成分y1,y2,y3,y4,y5,y6作为输入层元素，预测的脱硝效率值作为单一输出。

在Matlab中，相关参数设置如下：BP网络结构为6-4-1(6个输出层节点，4个隐含层节点，1个输出层节点)，隐含层函数使用tansig函数，输出层函数选用purelin函数。迭代次数为1 000，学习率为0.1，学习目标为0.000 1，灰狼种群数为40，个体编码长度为33，最大进化次数为10 000，初始位置范围为[-1,1]，式(9)中的k值为2。

为了验证IGWO-BP算法效果，在MatlabR2016a仿真平台下建立3种脱硝效率预测模型。分别为：1)传统BP神经网络模型；2)传统GWO-BP神经网络模型；3)IGWO-BP神经网络模型。3种模型共用一套由4 000组原始脱硝数据随机抽取后的训练与检验数据。并采用平均绝对误差MAE、平均绝对百分比误差MAPE与拟合优度R2作为评价标准比较3种模型，3种评价标准计算公式为式(19)～(21):

(19)

(20)

(21)

按照前述方法建立的IGWO-BP模型对训练样本脱硝效率预测训练效果如图5所示，3种模型间评价参数如表3所示。IGWO-BP模型预测误差绝对值与BP模型及GWO-BP模型对比如图6、图7所示。

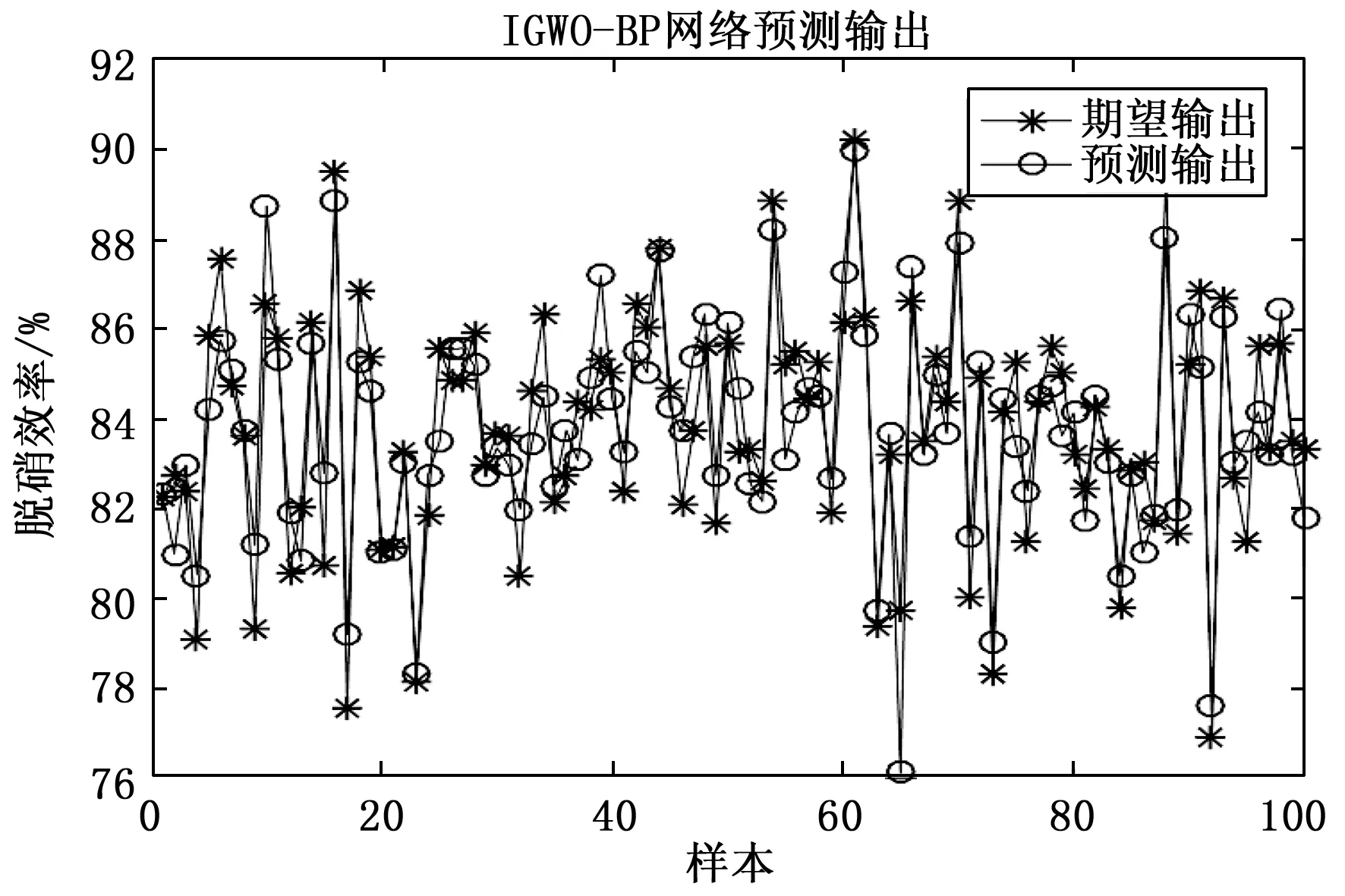
图5 IGWO-BP神经网络预测结果

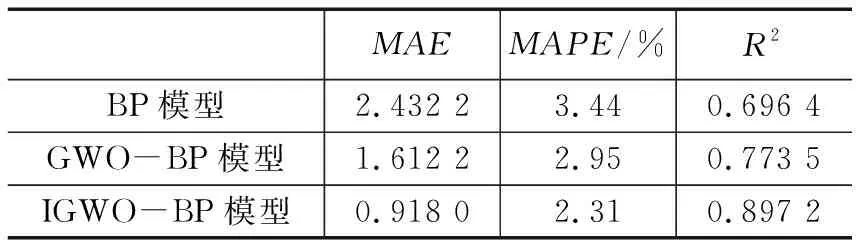
表3 3种模型预测效果对比

由表3分析可知，IGWO-BP预测模型下平均绝对误差MAE相较传统BP模型减小62.62%，平均绝对百分比误差MAPE降低48.92%，拟合优度R2增加28.83%；IGWO-BP预测模型相较传统GWO-BP模型MAE减小43.06%，MAPE降低21.69%，R2增加15.99%。由图6、图7可以看出，IGWO-BP、传统GWO-BP与BP模型预测结果最大误差绝对值分别为3.61%、4.13%与6.67%，IGWO-BP模型下的预测效果明显优于传统BP模型，与GWO-BP模型相比，虽然个别点预测精度不如GWO-BP，但整体上预测效果优于GWO-BP模型。

图6 传统BP与IGWO-BP预测误差对比

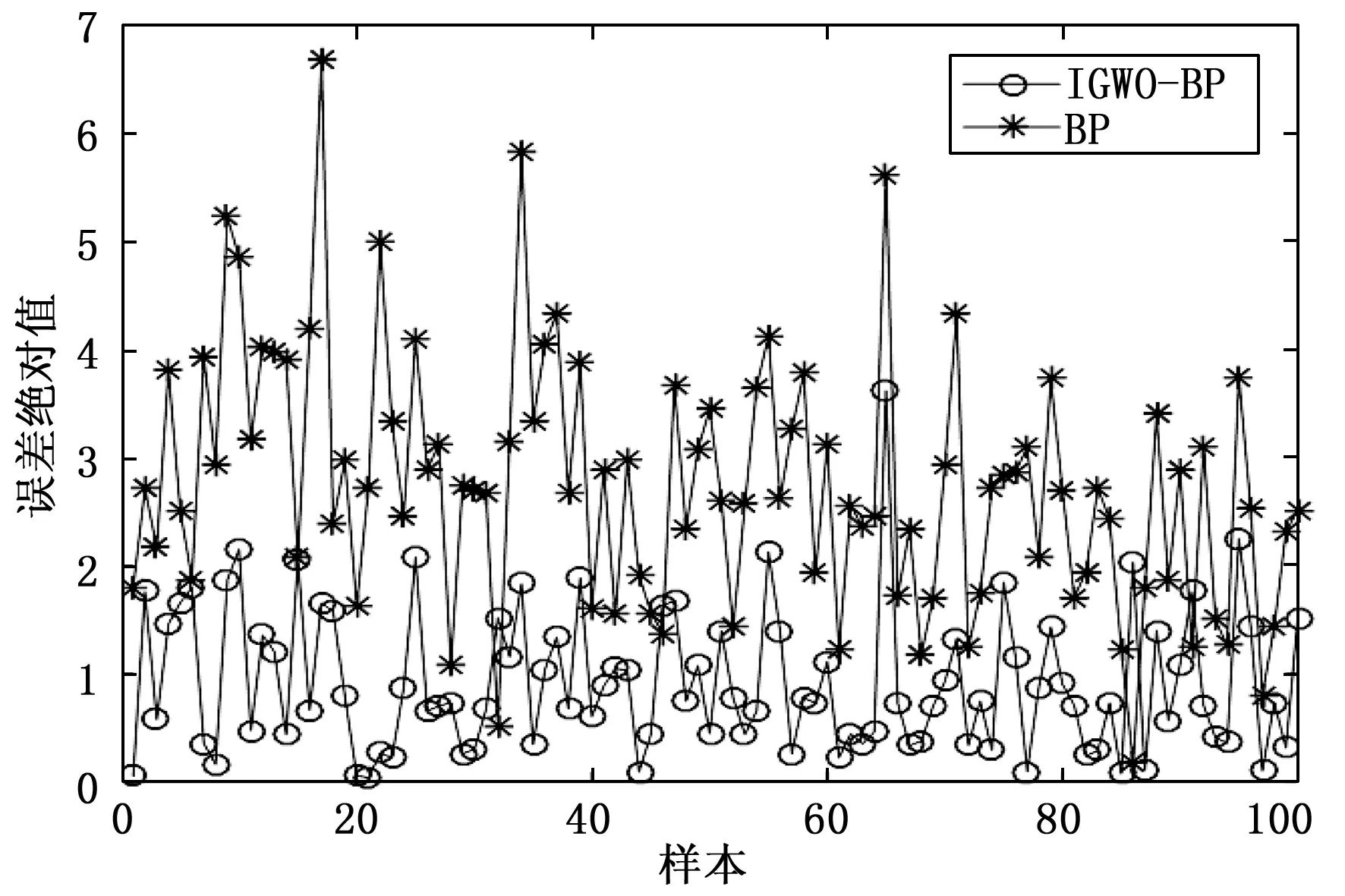
图7 GWO-BP与IGWO-BP预测误差对比

3 结束语

提出一种将改进灰狼算法与BP算法相结合，应用于燃煤电厂脱硝效率软测量的方法。将影响脱硝效率的因素通过主成分分析法降维成少数几个有代表性且互相独立的因素。再利用改进灰狼算法的优势，对传统BP算法进行优化，得到大唐洛河发电厂6号机脱硝装置预测模型。通过结果可知，本方法一定程度上提高了预测精度，改善了传统BP网络可能陷入“局部最优解”的缺陷，可用于电厂脱硝效率的预测。