基于支持向量机回归的民用飞机航材消耗预测研究

曾浩然，冯蕴雯，路成，潘维煌

（西北工业大学航空学院，西安710072）

0 引 言

装备保障直接影响航空公司机队的正常运行，航材作为装备保障的关键部件，其精确化保障在降低库存管理成本、优化资金分配、提高飞行安全等方面有重要作用，而航材消耗预测方法的准确性是实现精确化保障的基础。目前主要的航材预测技术可概括为三种：基于时间序列法的预测技术、基于回归分析法的预测技术和基于机器学习的预测技术［1］，每类预测技术还包括多种方法。

时间序列预测方法中指数平滑法最为经典，因其原理简单易懂、操作方便，成为航材消耗预测研究中最常用的方法［2-4］。毕钊等［5］综合考虑季节变动、中长期趋势以及随机干扰等因素之间的相互作用，改善时间序列法短期预测精度不高的问题；J.D.Croston［6］则考虑了时间间隔与消耗历史等因素，基于指数平滑法提出Croston方法用于航材预测，但现实中很多需求都不符合正态分布，因此该模型预测精度不高；R.H.Teunter等［7］使用英国皇家空军的大型数据集，将Bootstrap法用于预测间断型航材需求量，但在预测小样本集航材需求时效果不佳。指数平滑法对数据集的大小较为敏感，当样本量减少到一定程度，预测结果就会产生较大偏差［8］。

回归分析法通过建立目标输出与输入变量之间的关系，确定消耗与影响变量的关系式［1］。陈振林等［9］提出一种非参数回归的航材消耗模型，能较好地改善缺乏先验知识、预测周期长等问题；Guo F等［10］提出一种双层组合回归预测模型，进一步提高回归模型的预测精度。当涉及因素过多时，回归分析法的预测精度会降低，不能有效实现航材消耗预测。此外，当变量参数维数较高时，需要足够的样本支撑来实现回归分析模型的建立。

机器学习中最为典型的方法是人工神经网络和支持向量机。A.S.Vander等［11］基于航材消耗信息，利用人工神经网络模型进行航材需求预测；孙伟奇等［12］将最小二乘原理结合支持向量机应用于小数据集航材消耗预测，验证了该类方法在工程中的适用性。

本文以回归原理为基础，结合支持向量机理论对航材进行预测，提出基于支持向量回归的航材预测模型，通过对比指数平滑法和支持向量机回归模型的预测结果，验证本文模型的有效性。

1 支持向量机回归预测模型

支持向量机（Support Vector Machine，简称SVM）现论于1995年提出，能够在小样本的前提下实现非线性和高维问题分析［13-15］，具有适应性强、训练时间短、泛化能力强等特点［16-19］。此外，SVM能够有效克服维数灾变和过学习等传统算法难以解决的问题［20-23］。

SVM主要包括支持向量机分类和支持向量机回归（Support Vector Regression，简称SVR），目前两种方法已在很多领域得到广泛应用［24］。航材消耗预测实质上属于回归分析，结合航材消耗历史数据进行下一阶段或下一时刻点的需求预测分析［25］。利用SVR建立预测模型的步骤如图1所示。

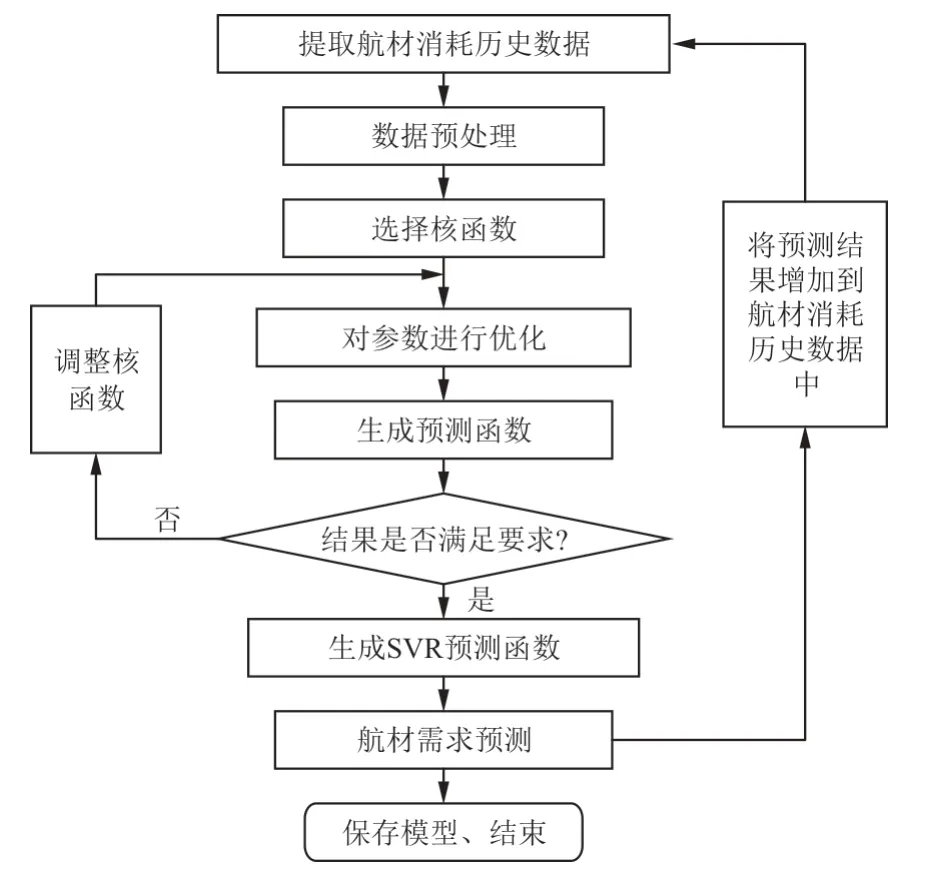
图1 基于支持向量机回归的航材预测模型建立步骤Fig.1 Support vector machine regression-based aircraft material forecast model building steps

首先进行数据预处理，将数据划分成训练数据集和预测测试数据集，然后将训练数据集输入模型进行训练，得到训练后的SVR模型。其中训练过程的原理为：通过引入非线性算子函数φ，把初始样本映射到高维空间，并在高维空间对初始样本进行处理，通过这种方法能够将非线性预测问题变为高维度上的线性预测问题，这样就可以把一些较为复杂的运算简单化［26］。最后，将预测测试数据输入训练后得到的模型中进行回归计算，输出预测结果。SVR基本原理介绍详见文献［27］。

2 典型国产民用飞机航材消耗预测案例

本节针对某型飞机的LRU航材历史消耗数据进行分析研究。该组数据共有36期消耗值，选取前31期消耗量数据作为初始训练数据（如表1所示），最后5期作为预测测试数据（实际消耗值），用以分析预测模型的实际效果。

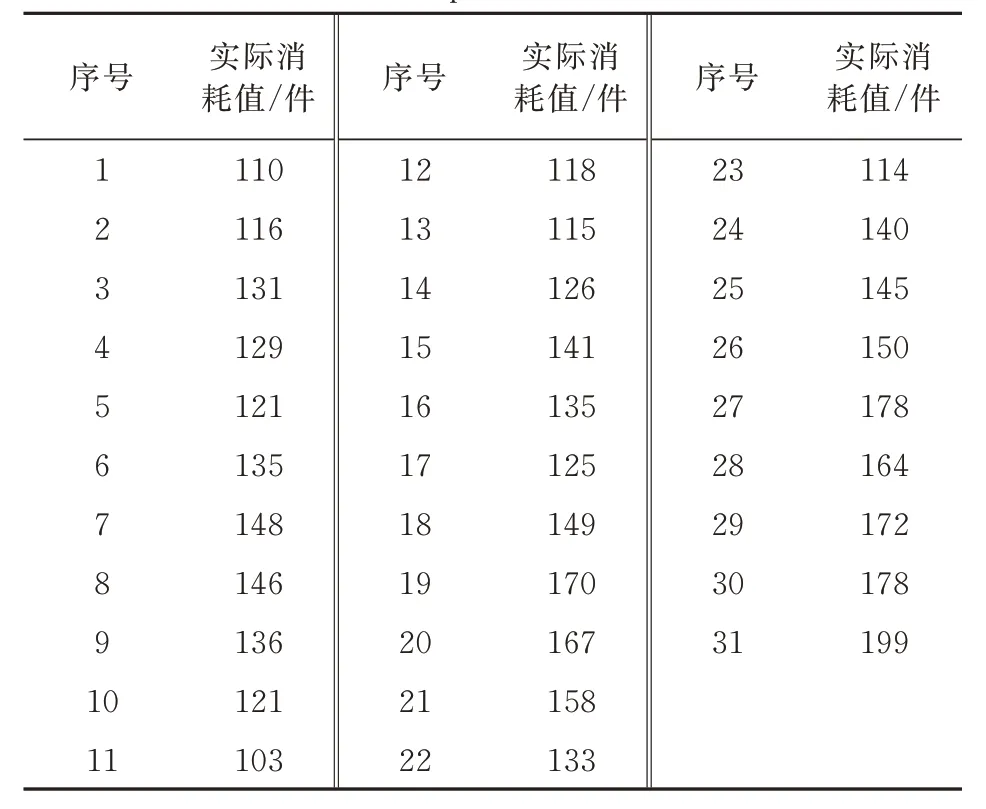
表1 航材消耗量预测训练样本Table 1 Training samples for aviation material consumption forecast

模型的核函数选用径向基核函数（Radial Ba‐sis Function，简称RBF），惩罚系数C和核参数g运用网格搜索法对其进行优化，最终选择C=1 024，g=0.031 5。其预测结果如表2所示。

表2 航材消耗预测测试样本与预测值Table 2 Test samples and forecasted values for aviation material consumption forecast

整理表2数据并绘制航材历史消耗与预测曲线，如图2所示。

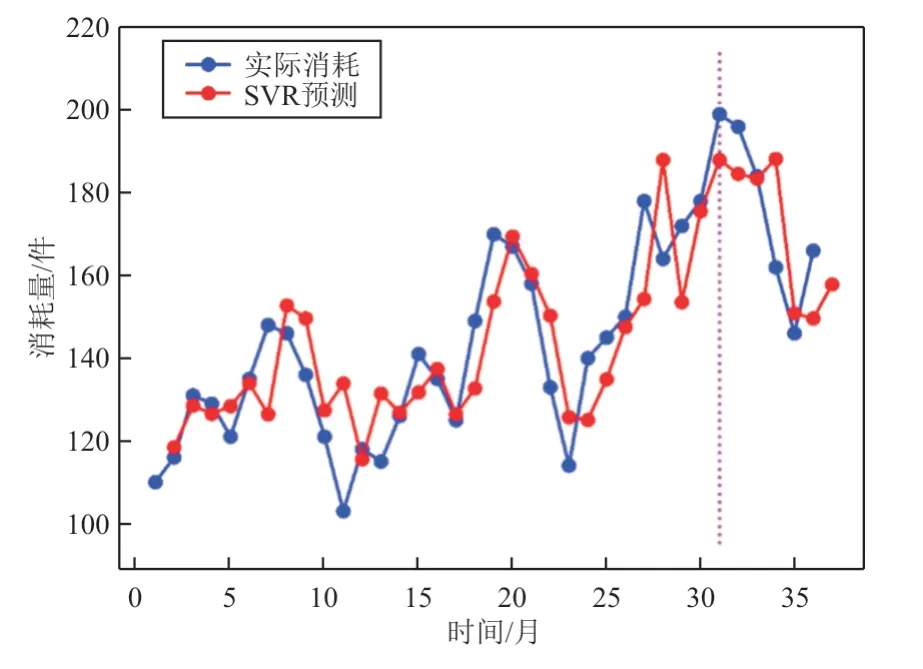
图2 实际消耗与SVR预测曲线Fig.2 Actual consumption and SVR forecasted curve

3 预测精度对比分析

将相同的数据分别输入到一次、二次和三次指数平滑模型中进行预测对比分析。

为有效评价模型拟合效果，使用以下两个指标分析不同模型的预测准确性：

（1）平均绝对误差MAE

数学表达式为

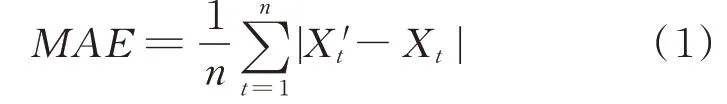
（2）平均绝对百分比误差MAPE

数学表达式为

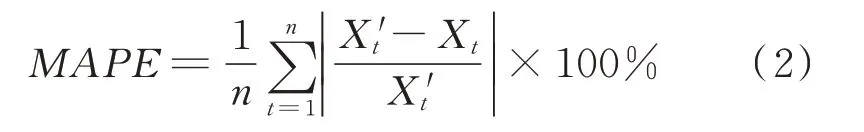
式中：Xt'为观测值；X t为预测值。

同样选取前31期历史消耗量作为初始训练数据，最后5期作为预测测试数据，取第1期消耗数值最为初始平滑值。一次、二次、三次指数平滑法的平滑系数均为0.9，预测结果如图3所示。

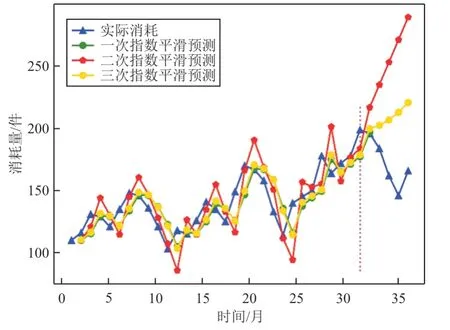
图3 实际消耗与指数平滑预测曲线Fig.3 Actual consumption and exponential smoothing forecast curves

通过式（1）和式（2）计算得到SVR模型的MAE和MAPE结果如表3所示。

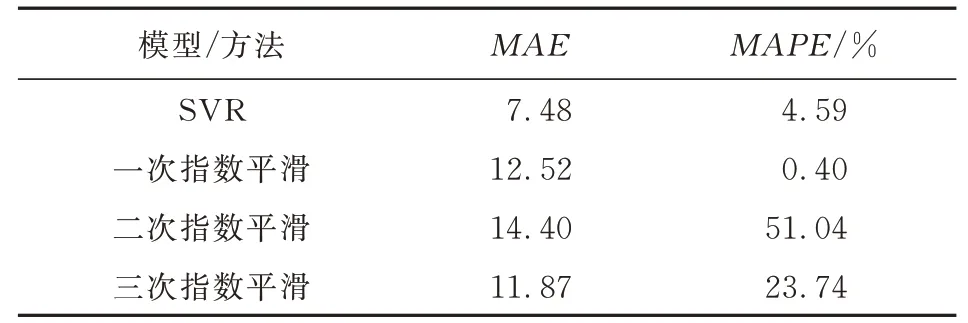
表3 多种预测模型平均绝对误差和平均绝对百分比误差Table 3 Mean absolute error and mean absolute percentage error of multiple prediction models

从图2~图3可以看出：SVR模型得到的预测曲线对实际数据的拟合程度优于指数平滑法。再结合表3可知，SVR模型的MAE=7.48，小于三种指数平滑法的11.87、14.40和12.52。由于一次指数平滑法具有只能预测一期的特点，其MAPE低于SVR模型，但SVR模型的MAPE为4.59%，显著小于二次、三次指数平滑法的51.04%和23.74%。

综上所述，SVR的预测效果好于指数平滑法，将支持向量机回归理论应用到航材消耗预测领域有助于提升航材的精细化保障水平。

4 结 论

（1）在某型航材样本数据较少、预测周期较短的情况下，支持向量机回归模型对消耗变化趋势的拟合效果强于指数平滑法，且具有更小的平均绝对误差和平均绝对百分比误差，该方法预测精度优于指数平滑法。

（2）支持向量机回归模型较为有效地解决了传统时间序列法难以解决的小样本航材预测问题，为推进装备精细化保障提供了一条可行的、有效的新途径。