基于TARAM的民用飞机结构类事件的持续运营安全评估
贾宝惠,马语蔚,王卓,王毅强
(中国民航大学交通科学与工程学院,天津300300)
0 引 言
风险和安全一直是民航业的重要考虑因素[1],为了保证飞机的持续适航性,民用运输飞机在投入运营前均通过了型号合格审定,但在实际运营过程中,由于标准制定或者标准符合性验证等方面存在未知的变化,飞机设计与制造方面存在缺陷,以及存在意料之外的状况,会导致飞机在运行阶段出现未能预料的故障或失效情况[2]。民航当局和飞机制造商需要根据收集到的故障或故障信息,评估该故障对受影响机队造成的不安全后果,当受影响机队的风险高于适航要求时,则该机队将处于不安全状态。为了保证机队的持续适航性,民航当局或制造商需要制定纠正措施[3-4],但纠正措施往往很难在短时间内全部完成且随着暴露时间的增加,不安全事件的风险也会相应增加[5],因此还需要针对纠正措施确定合理的实施时限,以保证机队的运营安全。
国外对于风险评估的研究较早,美国联邦航空局(FAA)的运输部致力于运输类飞机的持续运行安全(COS)。运输飞机风险评估方法(TARAM)[6]提供了用于运输类飞机的风险分析方法和可接受风险指南。FAA在TARAM方法中研究了个人风险、机队风险等5种风险值,用于判断受影响机队是否处于不安全状况,在AC39-8通告[7]中利用暴露时间内的风险因子和每飞行小时风险评估机队安全状态。EASA在其冈斯顿方法中介绍了纠正措施实施时限的确定方法,通过每飞行小时风险与机队的风险水平来确定纠正措施的实施时限[8]。
国内对于风险评估的相关研究起步较晚,但也取得了一定的研究成果。王冠茹等[9]结合风险管理理论,针对民用飞机运行阶段的不安全事件,建立了风险评估流程;李龙彪等[10]基于未纠正机队风险、90天机队风险和控制方案机队风险三类机队风险,针对常失效率故障建立了风险评估模型;郭媛媛等[11]针对磨损失效故障,结合机队历史运行数据建立了单机和机队风险评估模型;张子文等[12]建立了基于蒙特卡洛仿真的运输类飞机耗损失效场景的风险评估模型;Guo Y等[13]建立了包括当前风险水平、可接受程度、纠正措施时限的剩余风险确定流程;郭媛媛等[14]还给出了故障模式影响分析方法和故障树分析方法相结合的单机风险评估方法,并提出机队风险计算模型,以及在耗损失效期提出未纠正机队风险分析方法,还对各种方法适应情况进行了分析归纳,预测单机和机队运行期间的风险。
上述研究针对常失效率和磨损失效的故障建立了风险评估模型,但针对民用飞机结构裂纹故障风险的评估过于保守。本文基于运输飞机风险评估方法(TARAM),考虑飞机的不同裂纹尺寸,给出威布尔参数的计算方法,并建立风险评估流程,针对某型号飞机机身裂纹进行风险评估,计算该裂纹事件的个人和机队风险水平,以及纠正措施实施时限。
1 机队风险与个人风险
在民用飞机的持续运行期间,利用个人风险和机队风险两个安全指标,对整个机队的安全水平进行评估。
1.1 机队风险
风险的关键指标之一是机队风险RT,它是在不采取任何纠正措施的情况下,在剩余寿命内受影响机队预计会造成的乘客死亡率,表示为
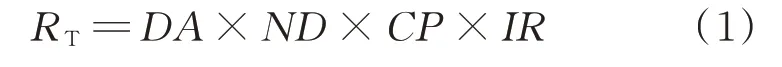
式中:DA为在受影响机队的剩余寿命内预计有故障的飞机数量;ND为在导致不安全后果之前未检测到故障发生的概率;CP为飞机不安全后果发生的条件概率;IR为死亡率。
(1)DA计算
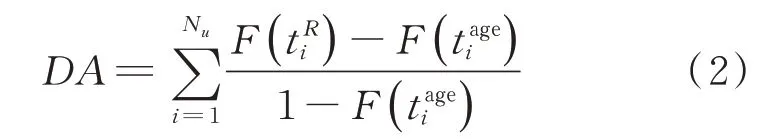
式中:F(t)为累积分布函数的威布尔分布;N u为到目前为止未出现裂纹的飞机数量,但这些飞机在剩余寿命内仍然可能会出现裂纹;tagei为第i架飞机目前的年龄;t Ri为飞机的退役年龄。
(2)未检出率ND
ND可以认为是条件概率的一部分,在民用飞机的运行和维护过程中,结构产生裂纹之后,未能以任何方式发现结构裂纹,从而导致不安全的后果,因此它是结构裂纹问题中的一个重要因素,需要单独进行分析。因为不同的部件考虑的因素会有很大的不同,所以分析不同结构裂纹时需要建立针对性流程图以确定其未检出概率。
(3)确定不安全后果
裂纹导致的不安全后果可利用因果链进行分析,从研究故障发展至不安全后果需要经历多个状态,造成最终不安全状态的条件概率为

式中:P0为研究故障概率;Pi为中间状态的转移概率。
单一故障可造成多种不安全后果,每种不安全后果使用死亡率进行表示,条件概率CP和死亡率IR可利用历史统计数据进行计算。因此,该故障引发的总不安全后果为
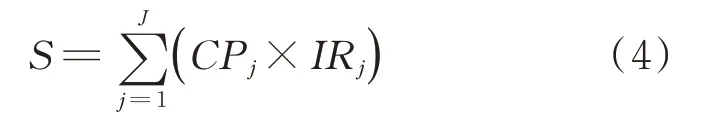
式中:S为总不安全后果的严重程度;J为故障可导致的不安全后果的数量;CPj为第j个不安全后果发生的概率;IR j为第j个不安全后果的死亡率。
1.2 个人风险
个人风险RI是机队中任意一架飞机上的机组和乘客在每个飞行小时面临的最高死亡率。
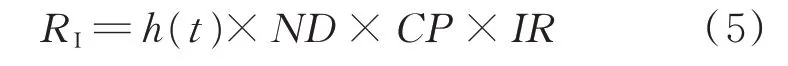
式中:h(t)为研究故障的故障率函数,表示部件工作到时刻t时尚未出现故障,t时刻后的下一单位时间发生故障的概率。
2 考虑不同裂纹尺寸的威布尔参数的计算
在民用飞机结构裂纹数据处理中,威布尔分布是最常见且拟合程度较好的分布[15]。由于民用飞机结构的可靠性较高,通常只有小样本数据,而威布尔分布在处理小样本数据时,相比其他方法具有较好的效果[16-17],为了更好地拟合民用飞机结构的失效情况,故本文采用威布尔分布。
参数β(形状参数)和η(特征寿命)由威布尔分析确定,通常使用从航空安全信息分析和共享计划获得的机队数据。当发生故障的飞机数量很少(即小于20架),可以使用威布尔贝叶斯方法。
在威布尔贝叶斯分析中,形状参数可以通过以往经验、历史失效数据和失效物理的工程知识确定[18]。
2.1 形状参数的确定
基于有关疲劳损伤可靠性分析报告[19-20]及FAA对于运输飞机的经验总结[21],列出可与威布尔贝叶斯方法相结合用于分析的威布尔形状参数值,如表1所示。

表1 形状参数估计值Table 1 Estimated shape parameters
2.2 特征寿命的确定
在已知形状参数的条件下,结合机队运行数据,将当前飞机飞行小时数作为故障时间,则特征寿命η为
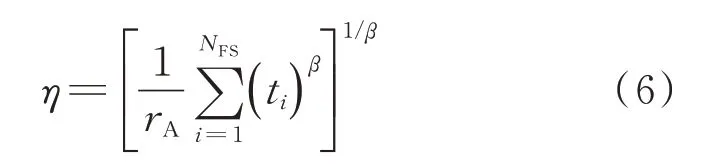
式中:rA为到目前为止已发生裂纹的飞机数量;NFS为受影响机队的飞机数量;ti为第i架飞机在发现裂纹或截止目前的飞行小时数。
因为受影响机队中飞机有不同尺寸的裂纹,有些飞机可能还没有裂纹,利用以上计算方法会导致结果较为保守,故本文将每架飞机的故障年龄设定为飞机出现临界尺寸裂纹的年龄。将受影响机队进行分组,具体情况如下:A组——最初发现有裂纹的飞机;B组——已被检查并认定为无裂纹的飞机;C组——没有被检查是否有裂纹,但已知没有发生危险事件的飞机。
通过以上划分,未发现裂纹的飞机不仅包括B组中的飞机,还包括C组中的飞机;C组飞机虽然未被检查过,但是它们没有临界尺寸的裂纹。因此,未发现裂纹的飞机数量N u是B组+C组的数量,NFS为A组+B组+C组的飞机数量,即受影响的整个机队。
对于A组中发现裂纹的飞机,裂纹从观测时的尺寸发展到临界尺寸增长所需的时间需要与观测时的运行时间相加,并作为其故障时间。tmi为通过目视检查发现裂纹时的年龄,tmo为从目视发现的裂纹尺寸扩展到临界尺寸的时间。因此,故障时间取ti=tmi+tmo。
对于B组来说,通过检测但未发现裂纹,从产生裂纹发展至目视可发现的裂纹尺寸需要一段时间tdm。裂纹从产生并增长到临界尺寸所需时间为tdm+tmo,因此,故障时间取ti=tagei+tdm+tmo。
对于C组来说,因未经过检查,故该部分飞机的裂纹情况是未知的,故障时间保守取ti=tagei。
3 民用飞机结构裂纹风险评估流程
3.1 风险准则
实际风险计算结果需要与持续安全风险准则进行比较,以确定受影响机队的风险是否可接受,并制定相应的风险控制措施。根据AC-21-AA-2013-19的要求,持续适航阶段的实际风险平均水平应保持在飞机设计允许的最大风险水平之内。参考TARAM准则,对于飞机结构裂纹事件导致的个人风险水平必须低于1×10-7/fh。同时,飞机结构裂纹事件导致的机队风险水平必须低于0.02。
将风险准则划分为4个区域,如图1所示,当机队风险小于0.02,且个人风险小于1×10-7/fh,受影响机队的风险处于可接受水平,机队处于适航状态,无需采取纠正措施;当机队风险高于0.02,或个人风险高于1×10-7/fh,受影响机队的风险为不可接受水平,机队处于不安全状态,需要采取纠正措施。其中部分飞机由于利用率和使用年限的影响使得个人风险较大,当个人风险大于1×10-7/fh但小于1×10-6/fh时,此时处于过度风险,需要制定纠正措施降低风险;当个人风险大于1×10-6/fh但小于1×10-5/fh,需立即采取规则(IAR);当个人风险高于1×10-5/fh,需立即发布紧急适航指令。个人风险的计算值为机队在某一时刻的瞬时风险值,可用于判断乘客和机组在某一时刻是否处于不安全状态;机队风险的计算值为受影响机队在研究时间段内的风险值。两个指标的研究范围不同,个人风险为相对瞬时峰值,而机队风险为所研究时间段内绝对汇总值。因此,个人风险与机队风险不仅可作为评判受影响机队是否处于不安全状态的评价指标,还可将个人风险作为判断飞机纠正措施种类和实施紧迫性的指标。综上,需要机队风险与个人风险共同使用,用于评价受影响机队的风险水平及制定纠正措施。
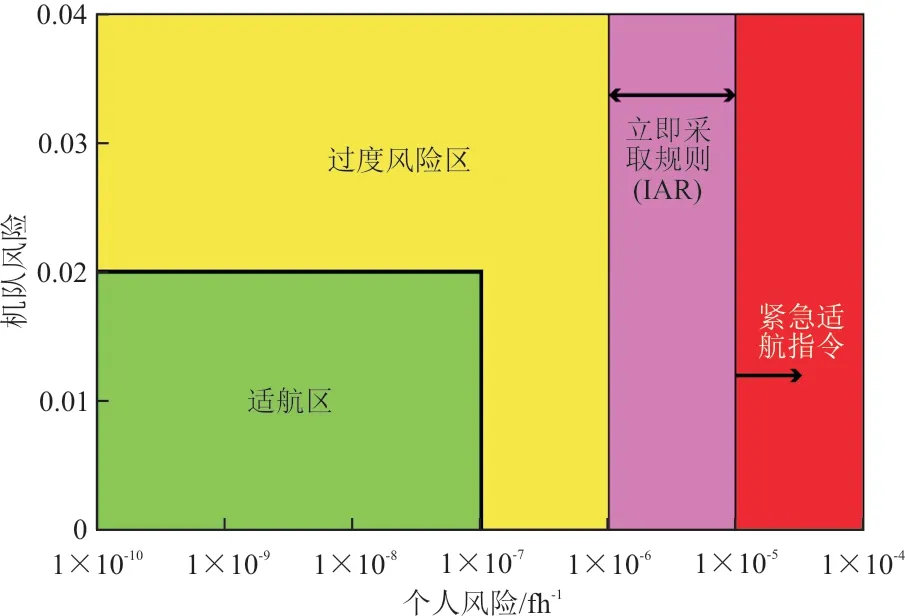
图1 TARAM风险指南曲线图Fig.1 TARAM risk guide curve diagram
3.2 基于TARAM的风险评估流程
风险评估流程包括以下步骤,如图2所示。
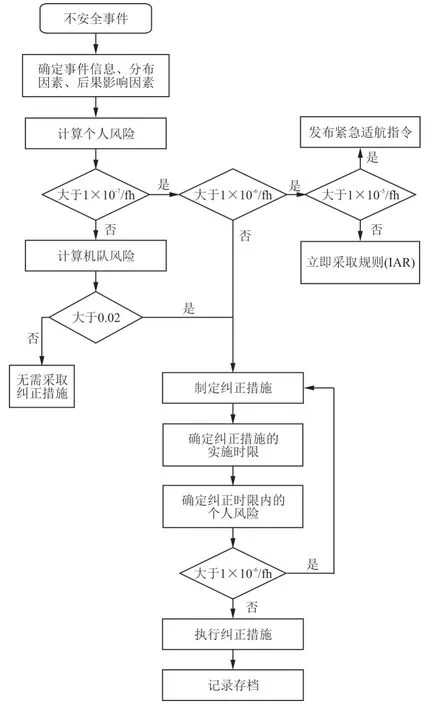
图2 基于TARAM的风险评估流程Fig.2 Risk assessment process based on TARAM
步骤1:在不安全事件的触发下,分析事件的发生原因及后果严重度,并收集受影响机队的相关数据。因结构裂纹的故障数据较少,故基于机队的运行及故障数据,利用考虑裂纹情况的威布尔贝叶斯方法对威布尔分布的参数进行估计,为机队故障风险评估提供支持。
步骤2:预测受影响机队在剩余寿命内的故障次数,并结合未检出概率、不安全后果的条件概率和死亡率计算机队风险;基于机队中服役时间最长飞机的失效率确定机队的个人风险;与风险准则进行比较,确定受影响机队是否处于不安全状态。
步骤3:在受影响机队处于不安全状态时,根据事件发生原因制定合理的纠正措施,并将0.02作为纠正措施实施时间内的机队风险阈值,绘制机队风险与实施时限关系图以确定出机队的纠正时限;利用纠正措施实施时限内的个人风险对纠正时限的合理性进行验证。
步骤4:记录存档。
4 案例分析
某航空公司的某型号飞机在维修过程中通过目视检查发现在STA 360和STA 380之间的左侧纵梁S-15位置的蒙皮上有一处受到循环增压载荷的疲劳裂纹。该结构为机身增压边界结构,属于主 要 构 件(Principal Structural Elements,简 称PSE)。如果不采取维修或更换蒙皮等纠正措施,蒙皮裂纹可能会继续扩展,机身蒙皮上的多个相邻裂纹可能会相互连接,最终可能会导致飞机减压等灾难性后果,因此该裂纹是一个不安全事件,需要进行风险分析。需要注意的是,该案例数值仅用于风险模型评估计算,不代表实际运营水平。
本次发现裂纹的飞机是在目视检查条件下发现的,裂纹并未扩展至临界裂纹尺寸,故认定该裂纹长度为中等长度,该架飞机的年龄为36 000 fc。通过收集、整理该机队的运行数据,可知受影响的机队规模为470架,此型号飞机的退役寿命为60 000 fc,利用率为250飞行循环数/月,平均每次飞行约1 h,该机队的飞行循环数如表2所示。
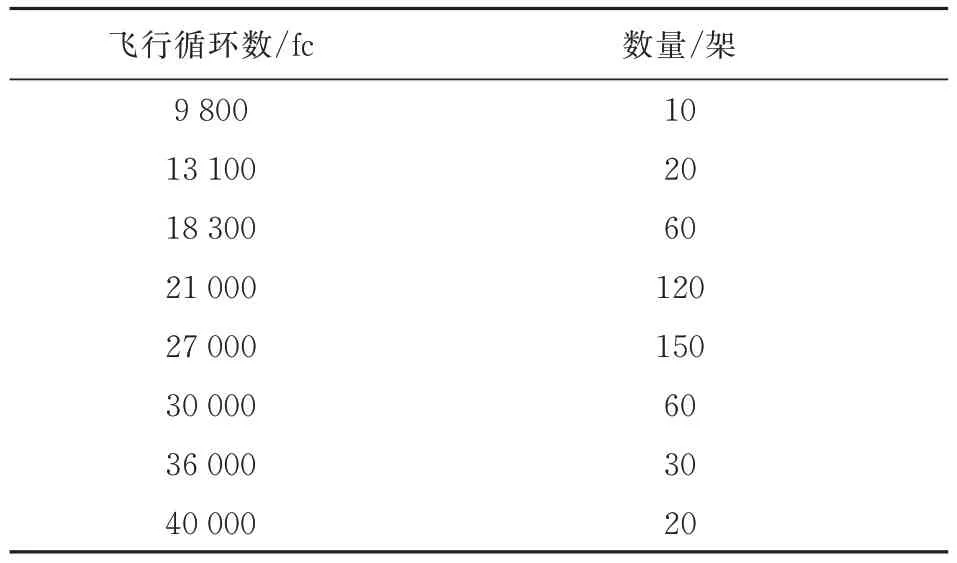
表2 机队役龄分布Table 2 Fleet life distribution
在检测率pinsp=0.1时,对其他46架飞机进行裂纹尺寸检测,抽检飞机年龄分布如表3所示。

表3 抽检飞机役龄分布Table 3 Distribution of sampling aircraft
在完成检测的飞机中发现2架飞机出现裂纹,未进行检测的飞机因为没有经过检查,所以不知道它们是否有裂纹。因此按照分组规则可知,A组的飞机数量为3架,B组的飞机数量为44架,C组的飞机数量为423架。
在威布尔分析中,受影响机队飞机的退役寿命t Ri=60 000 fc;形状参数β=4(材料为铝)。参考文献[22]中的方法,使用有限元分析方法确定裂纹长度从萌生至目视可见长度的增长时间为tdm=7 500 fc;裂纹长度从目视可见长度增长至临界长度的时间tmo=7 500 fc。计算出的特征寿命为
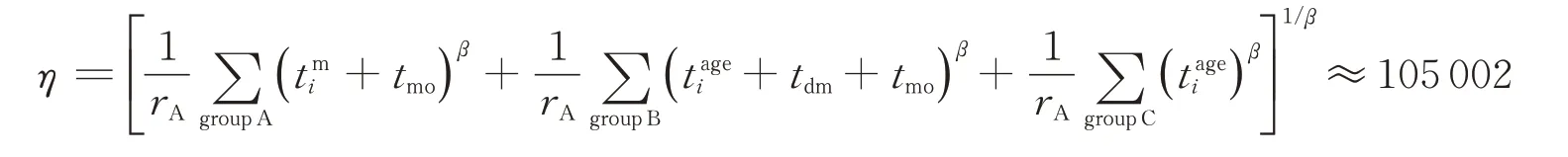
将计算出的威布尔分布参数带入累积分布函数,可得

许多发现的裂纹不是通过寻找特定裂纹的定向检查发现的,而是在正常操作和日常维护过程中偶然发现的。
本文参考文献[21]中的方法利用专家经验建立未检出概率确定流程,如图3所示,根据裂纹情况和检测手段确定出未检出概率ND=0.6。
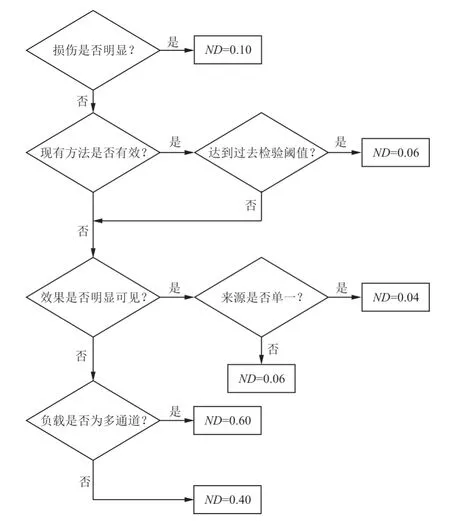
图3 未检出概率确定流程Fig.3 Undetected probability determination process
条件概率与危害度的确定依据故障发生后可能发生的事件以及不安全后果,进行事故因果链分析,如图4所示。
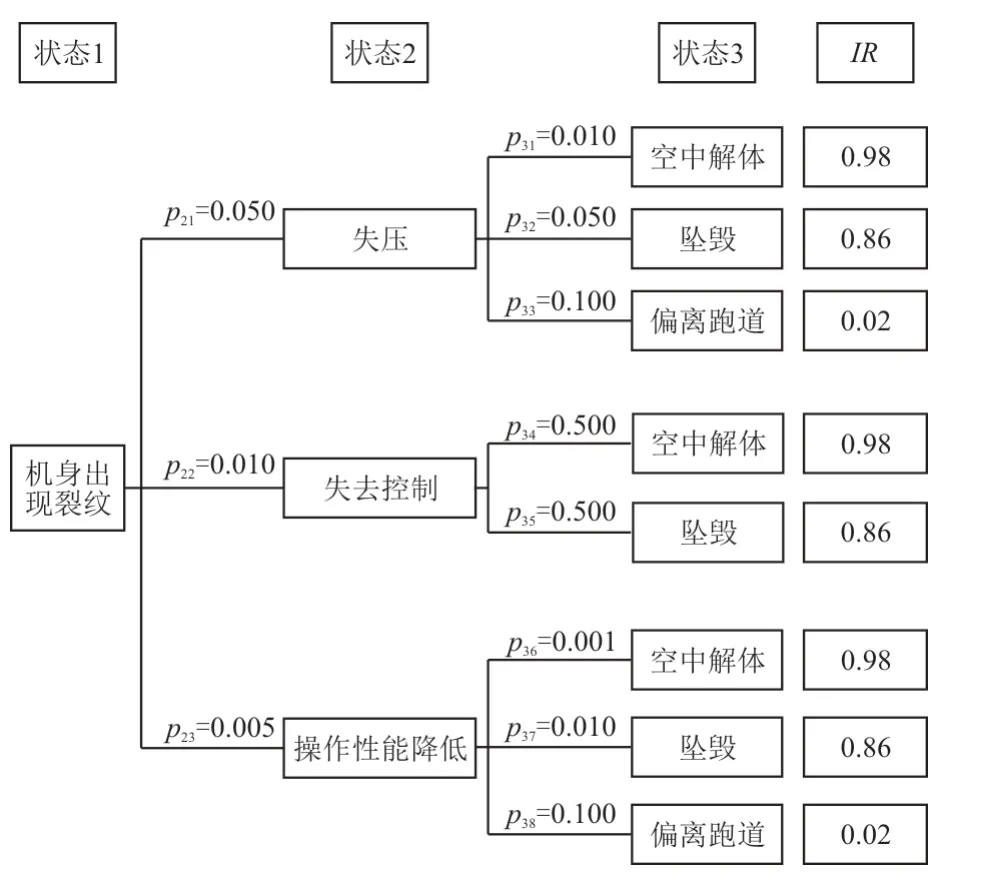
图4 机身裂纹故障因果链Fig.4 Fault causal chain of fuselage cracks
不安全后果的严重程度是通过不安全后果的统计死亡率来确定的。死亡率如表4所示。

表4 不安全后果的死亡率Table 4 ortality of unsafe consequences
根据图4中的条件概率和表4中的损伤率IR可以计算出机身裂纹造成的不安全后果的严重程度为∑( )CPi⋅IR i=0.012。进而可以确定在剩余寿命内的机队风险为
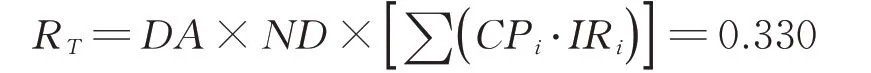
由于飞机年龄越大,个人风险越高,为了保证机队中每架飞机在每次飞行循环中风险不超过准则要求,需要评估最老的飞机在不采取纠正措施条件下的个人风险。
在已知威布尔参数条件下可知失效函数为

不采取纠正措施条件下最老飞机的飞行时间为退役年龄60 000 fc,因此,个人风险为

通过将计算得到的机队风险、个人风险与风险准则进行比较发现,个人风险为可接受水平,但机队风险处于不可接受水平,因此该机队处于不安全状态。通过研究分析,认为需要对机队中所有飞机在STA 360和STA 540之间,并位于S-14L至S-19L区域的蒙皮组件进行详细目视检查,并根据裂纹情况进行维修与更换,位置如图5所示,但实施该纠正措施需要一定的时间。为了确定纠正措施实施时限,本文将机队风险的指南0.02作为机队风险阈值。

图5 STA 360至STA 540蒙皮板组件Fig.5 STA 360 to STA 540 skin panel assembly
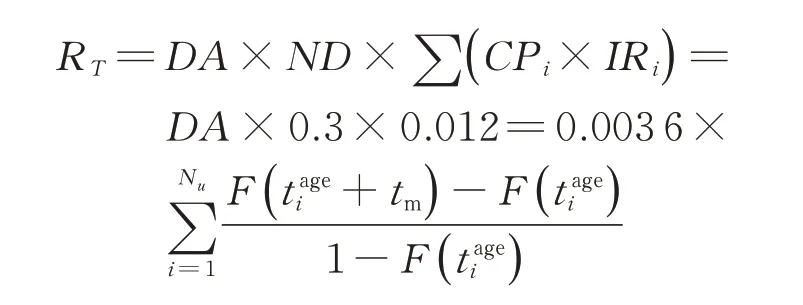
纠正措施实施时限tm可以有效地控制纠正措施期间的机队风险RT。以1个月(250 fc)为单位,分别计算纠正措施实施时限为1月至40月的机队风险水平。机队风险与纠正措施实施时限之间的关系如图6所示。
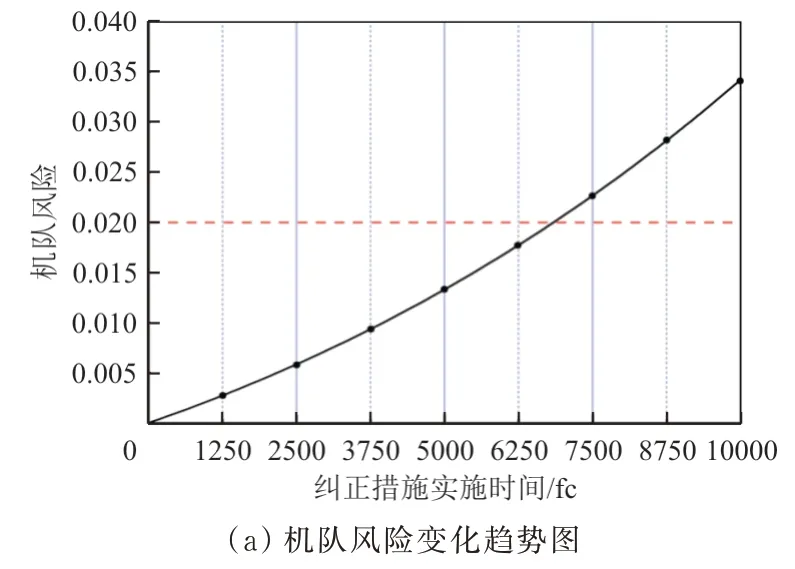
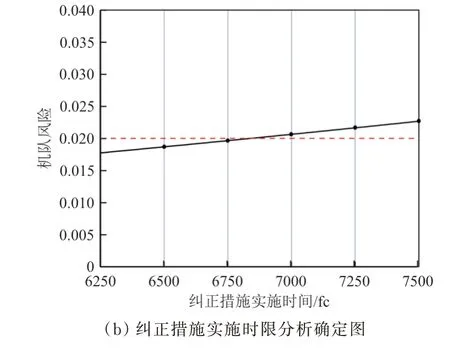
图6 机队风险与纠正措施实施时限之间的关系Fig.6 Relationship between fleet risk and implementation time limit of corrective measures
从图6可以看出:为保证机队安全,该机队的纠正时限为27月(6 750 fc),即制定的全面检查的纠正措施需要在该纠正时限内完成。
由于该机队年龄分布较为分散,为了保证每架飞机在每次飞行中的安全,本文使用纠正措施实施时限内受裂纹事件风险影响的个人风险进行验证。
从图7可以看出:个人风险在纠正措施实施时限内,未超过风险阈值1×10-6/fh,因此,可以认为本文制定的纠正措施及实施时限满足机队持续安全要求,可保证该机队的运行安全。
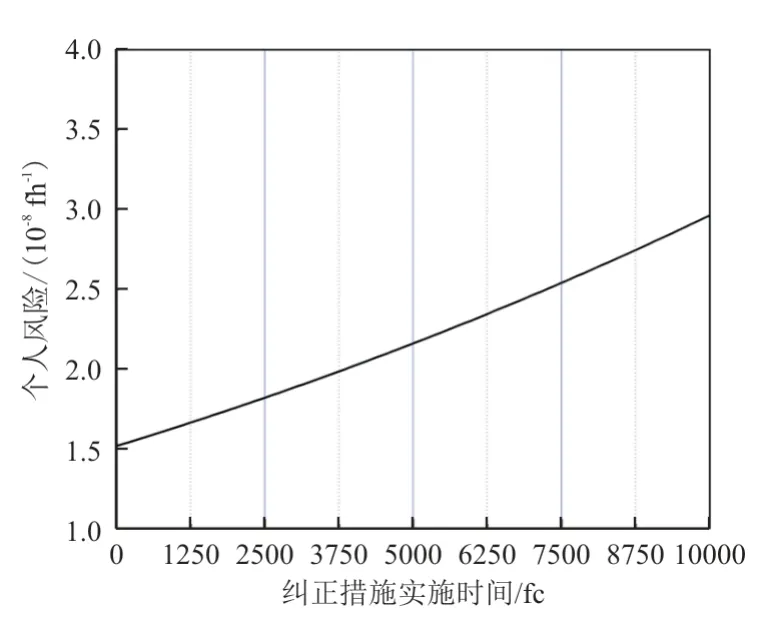
图7 个人风险与纠正措施实施时限之间的关系Fig.7 Relationship between individual machine risk and implementation time limit of corrective measures
5 结 论
(1)因为受影响机队中飞机有不同尺寸的裂纹,有些飞机可能还没有裂纹,因此,将每架飞机的故障年龄认定为飞机出现临界尺寸裂纹的年龄更为合适。
(2)确定纠正措施后,应评估纠正措施条件下的个人风险,即使用纠正措施实施时限内受裂纹事件风险影响的个人风险进行验证,以证明采取的纠正措施满足持续安全的要求。

