最小二乘法在医疗服务系统中的应用

王子炫，许林瑞，曾媛，黄晟祺，汪玉笳，李功权

（长江大学地球科学学院，武汉430100）

0 引言

在人们物质生活不断提高的今天，人们越来越关心自己的身体健康，去医院检查身体与看病的人越来越多。与此同时，党的十九大明确指出：“全面建立中国特色基本医疗卫生制度、医疗保障制度和优质高效的医疗卫生服务体系”。在进入移动互联网时代后［1］，“互联网+”这种新的经济形态的飞速发展，以及“智慧医疗”这一概念的提出［2］，使得各种基于互联网的服务产品层出不穷，产生了众多“互联网+医疗健康”的智能医疗服务系统。加之微信公众平台在2012年开放了第三方开发接口，这就意味着应用接口开放了［3］。

在这样的大环境下，团队开发出了基于GIS的就医无忧服务系统，该系统是一个基于SSM框架的Web系统，可以实现查询、人流分析展示、显示医院模型、数据上传、模拟预测等功能，具有操作方便灵活、图形化信息属性、显示直观清晰的特点。

医院每天的就诊人数是一个重要的数据，该数据作为医院业务水平的判断标准之一，也间接反映了去医院挂号排队的时间。因此，在基于GIS的医疗服务系统中，开发了数据上传和模拟预测这两大功能，可以看到某医院前一周的历史就诊人数以及预测的未来7天的就诊人数。这样，人们就可以根据系统预测的医院就诊人数来计划安排就医或体检的行程。该功能从已知的每日医院就诊人数出发，通过建立数学模型来预测未来一周内医院的就诊人数。

最为广泛使用的便是最小二乘法，它通过寻找残差平方和的最小值来寻找数据的最佳函数匹配［4］。最早使用最小二乘法是在1801年，天文学家朱赛普·皮亚齐发现第一颗小行星——谷神星，数学家高斯发明最小二乘法预测了谷神星的精确位置。之后，最小二乘法被应用于机器学习与曲线拟合等诸多科学领域，具有简便高效、精准性高等优势。

1 应用技术

1.1 SSM框架

基于GIS的就医无忧服务系统采用SSM框架，SSM框架包含Spring、Spring MVC以及MyBatis这3部分。Spring由IoC和AOP组成［5］，用于程序的解耦；Spring MVC是Spring的一个子框架，用于简化Web开发；MyBatis封装了JDBC，用于操作数据库。这三者进行整合便形成了SSM框架。

这三者之间的关系就是，用户向Spring MVC发送请求，由Spring MVC判断是否需要从数据库中获取数据，如果需要，MyBatis会获取数据返还给逻辑层，之后Spring MVC将得到的数据交由Dispatcher进行渲染，最后展现用户界面。

1.2 My SQL数据库

传统的数据管理模式都是将数据以文件形式存储，所有数据都被放在一个大仓库内，而关系数据库将数据保存在不同的表中，这样不仅提高了读取速度，也让数据库具有较高的灵活性。MySQL是一个开源的关系型数据库，该数据库相对于其他数据库来说体积更小，并且具有很好的移植性［7］。

MySQL是一种在服务器上运行的数据库系统，它几乎可以在所有平台上运营，包括UNIX、Linux、Windows，而且体积小到甚至可以安装服务器在自己的PC中，可靠、可拓展、运行速度快，是目前为止在Web应用方面最好的关系数据库管理系统。

1.3 最小二乘法预测原理

首先，获取到数据，这些数据包含两个变量，即自变量x和因变量y，在坐标系中将这些成对的数据表示成（x,y）的点。但是这些点成离散分布，依靠仅有的相关关系并不能计算出经过这些点的函数，所以，需要引入函数f(x i,θ)近似模拟对应关系［8］。当真实值与计算值的差平方最小，即残差的平方和最小时，拟合效果最好，残差的平方和用δ表示。当θ的取值使得δ的值最小时，f(x i,θ)就是根据数据拟合出来的回归方程。

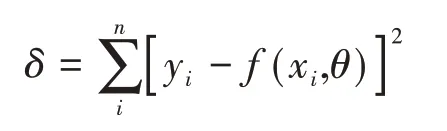
通常使用最小二乘法进行拟合时，要让δ对θ求偏导，再使用迭代法计算出θ，但是在预测医院就诊人数这个模型中，数据关系较为简单，因此，我们引入的对应关系为一元线性的，f(x i,θ)的形式变成了（1）式。

需要拟合的线性回归方程：

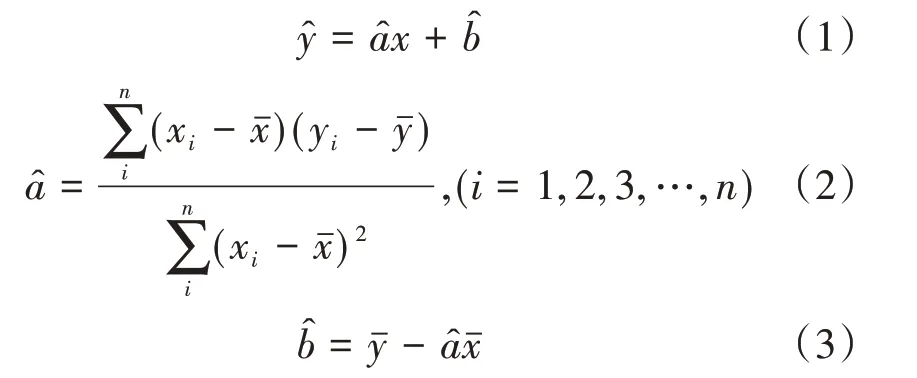
其中，式（2）可化简成下式：

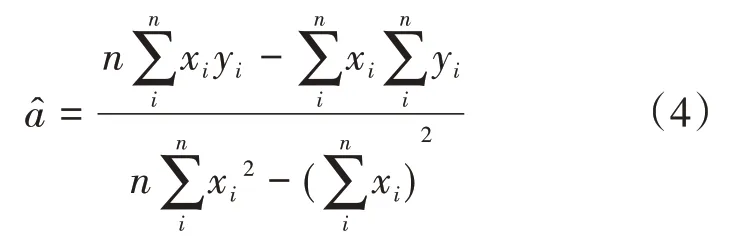
拟合出来的回归方程是满足残差平方和最小的，这样的回归方程预测的结果最为准确。

1.4 Quartz开源作业调度框架

Quartz是一个完全由Java编写的开源作业调度框架，为在Java应用程序中进行作业调度提供了简单强大的机制。Quartz允许程序开发人员根据时间的间隔来调度作业，可以设置触发器规定在相同的时间间隔内运行同一个模块，并且实现了作业和触发器的多对多的关系，还能把多个作业与不同的触发器关联。其12个包中组织有300个左右的Java类和接口，功能众多。

Quartz框架的核心是调度器，调度器是负责管理Quartz应用运行时环境的重要工具。

2 在系统中实现

2.1 数据获取与处理

将从网上获取到的某医院近10天的数据制成表1，为了计算方便，我们使用日期编号替代日期，3月1日编号为初始值1，3月2日编号为2，接下来以此类推。

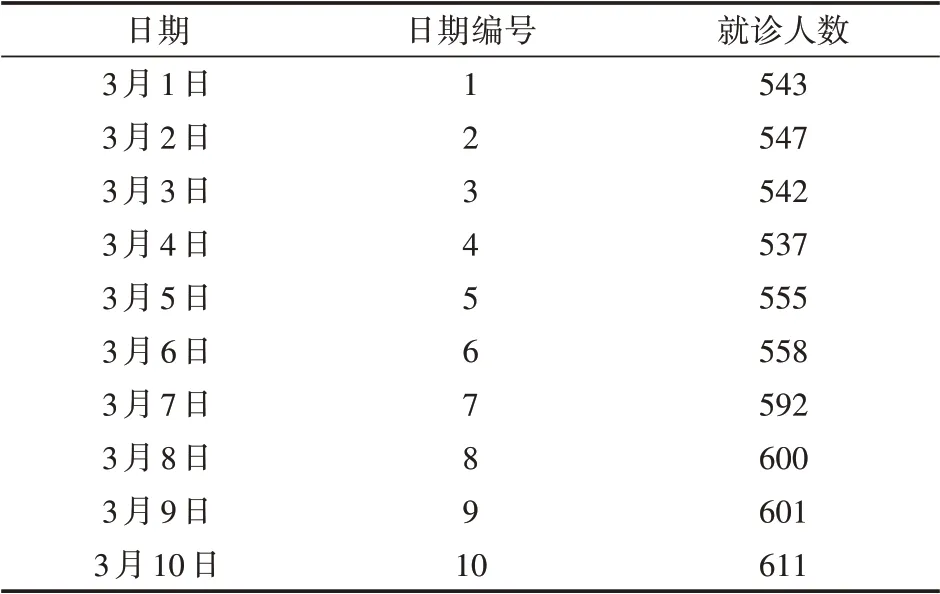
表1 2021年3月1日—3月10日某医院就诊人数

2.2 建立数学模型

从数据中可以看出，随着时间的变化，医院的就诊人数有着增加的趋势。我们将日期编号作为x轴，将就诊人数作为y轴。制作出就诊人数—日期散点图。

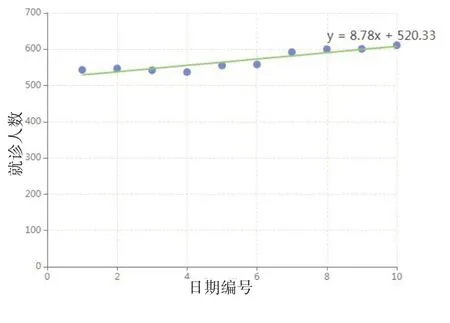
图1 2021年3月1日—3月10日就诊人数—日期散点图

根据散点图，使用最小二乘法进行拟合，计算出线性回归方程。将数据代入求出的值分别是8.78和520.33。

由此，我们得到关于日期和就诊人数的回归方程：

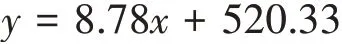
2.3 实现模拟预测功能

知道最小二乘法的原理后，需要在系统中实现预测功能。在后端中，我们使用Java语言进行代码的编写，创建LineRegressionUtils类来存放最小二乘这个功能。声明calCoefficientes方法用于计算（4）式中的各项值，声明train方法计算数据总量并调用calCoefficientes方法，最后声明predict方法输出计算结果，即：

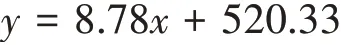
仅仅有一个类是不够实现对医院就诊人数预测这个功能的，我们使用了开源作业调度框架Quartz构建了一个触发器，使得该程序在每天的零点执行一次，来预测今后几天的医院就诊人数。

整个数据上传与模拟预测的流程是先使用Calendar.getInstance方法获取日历数据，之后使用.add（Calendar.DATE,-8）方法获取当日前7天的日期数据，并将其转化成double型数据类型，使用predictService.findMemberCountByDays方法来根据传入的日期查询相对应的就诊人数，并将其转化成double型数据类型。有了这些数据后调用之前的编写的LineRegressionUtils.train（x,y）方法计算回归曲线。之后按照同样的方法获取与处理后7天的日期数据，并通过Dubbo远程调用服务实现预测数据导入到数据库。

3 结语

在本文中，基于GIS的就医无忧服务系统采用最小二乘法对医院未来7天的就诊人数进行了模拟预测。医院的就诊人数是一个不确定的量，但是可以根据往日的数据，使用最小二乘法寻找到就诊人数与日期的相关关系，从而以此为根据进行预测。