基于内聚力界面的钨合金两相细观结构拉伸模拟

杨梓清

摘 要：在钨合金粉末冶金制备工艺的基础上，本研究建立了一种基于颗粒挤压方法的钨合金两相结构模型。首先在光学显微镜下观察了钨合金的微观组织结构，并统计了其颗粒分布特征，随后利用随机顺序吸附算法生成符合实际分布的颗粒初始构型，然后利用Python脚本程序在ABAQUS软件中建立颗粒挤压模型，以提高颗粒的体积分数。当模型模拟出的颗粒体积分数达到钨合金中鎢颗粒真实的体积分数时，提取颗粒边界轮廓，并运用布尔运算生成粘结相。最后通过Python脚本程序在颗粒界面生成内聚力单元，结合有限元方法，将上述模型运用于钨合金的拉伸模拟，确定了内聚力单元的参数，并与试验结果进行了对比验证，讨论了内聚力参数对拉伸应力-应变曲线的影响。

关键词：钨合金;细观结构;挤压模型;内聚力单元;有限元法;拉伸仿真

中图分类号：TB33;TB302.3文献标识码：A 文章编号：1003-5168（2021）15-0014-06

Abstract： Based on the powder metallurgy preparation process of tungsten alloy， this study establishes a dual-phase structure model of tungsten alloy based on particle extrusion method. First， the microstructure of the tungsten alloy is observed under an optical microscope， and its particle distribution characteristics are counted， subsequently， the random sequential adsorption algorithm is used to generate the initial configuration of the particles in line with the actual distribution， and then the particle extrusion model is established in the ABAQUS software using the Python script program to increase the volume fraction of the particles. When the particle volume fraction simulated by the model reaches the true volume fraction of tungsten particles in the tungsten alloy， the boundary contours of the particles are extracted and the Boolean operation is used to generate the binder phase. Finally， a cohesive force unit is generated on the particle interface through a Python script program， combined with the finite element method， the above model is applied to the tensile simulation of tungsten alloy， the parameters of the cohesion unit are determined， the test results are compared and verified， and the influence of cohesion parameters on the tensile stress-strain curve is discussed.

Keywords： tungsten alloy;microstructure;extrusion model;cohesion element;finite element method;tensile simulation

材料的宏观力学特性往往会受到其微观结构特征的影响，特别是高比重钨合金这种拥有复杂微观结构的两相材料。已有研究表明，钨合金的力学性能受其微观结构特征的影响[1-3]。比如，钨合金的平均颗粒半径会影响钨合金的拉伸性能，平均颗粒尺寸越小，钨合金的屈服强度和抗拉强度越大，表现出细晶强化效应;钨合金内部钨颗粒分布不均匀，会导致其拉伸性能下降;钨合金的钨含量增加，粘结相体积相对减少，钨-钨连接度增加，从而导致其拉伸性能和冲击性能降低。因此，在研究钨合金复杂的力学性能时，不能忽略其微观结构组织特征的影响。如今，科学技术飞速发展，有限元方法已经变得越来越成熟和完善，能够解决许多工程问题，而对于具有两相结构的钨合金，有限元仿真不应该局限于宏观尺度，而应该更进一步从细观角度考虑其微结构的效应。因此，建立真实有效的钨合金微观结构仿真模型具有重要意义，在细观尺度上研究钨合金的结构参数可以更好地解释钨合金力学性能差异的原因，这对钨合金加工制备方法的改进有一定指导作用。

1 钨合金微观结构

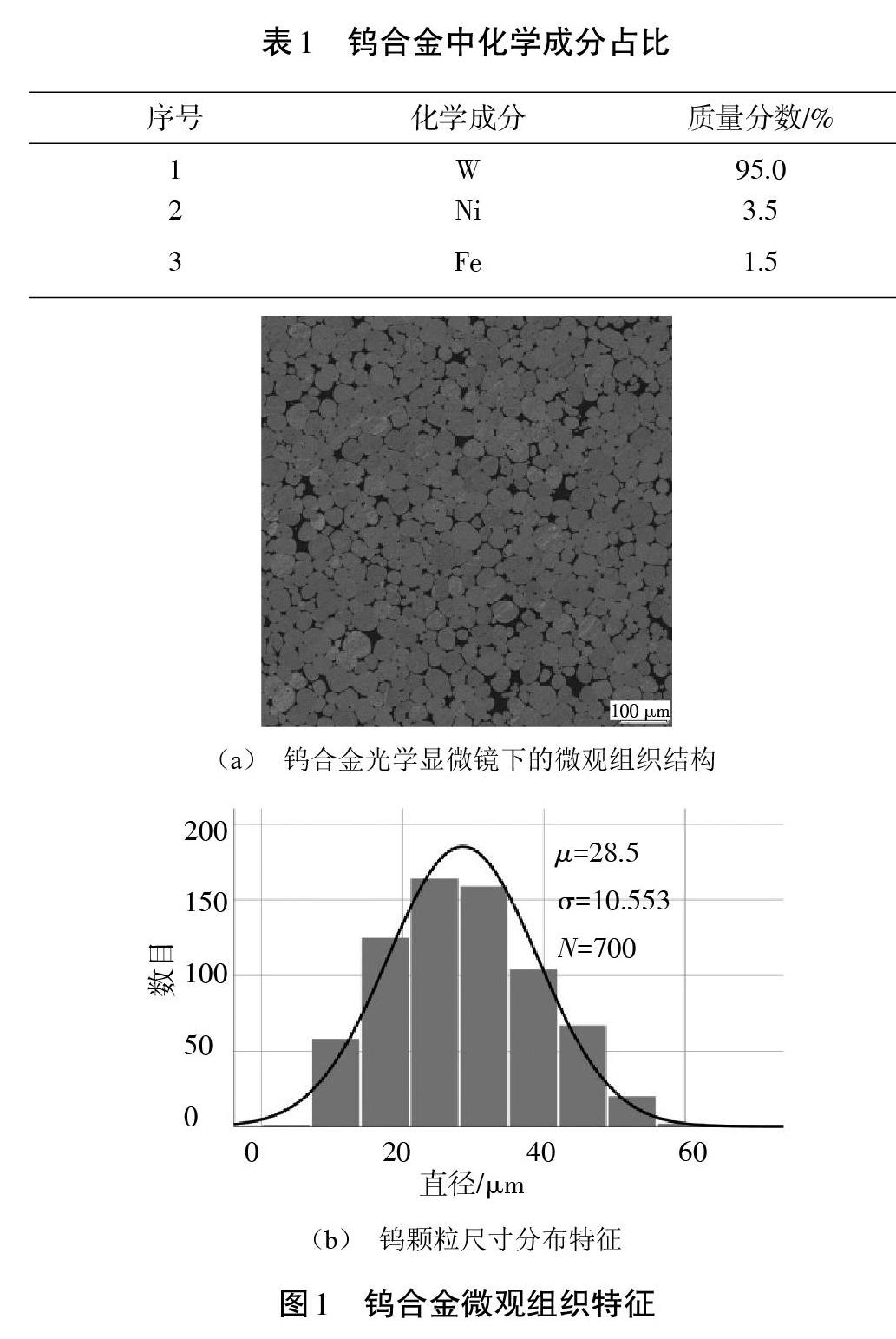
本文研究的钨合金为95W-3.5Ni-1.5Fe合金，其化学成分组成如表1所示。根据钨合金中每种元素的质量分数和密度可得，钨合金中，钨（W）颗粒的体积分数为89.8%，镍（Ni）和铁（Fe）颗粒的体积分数之和为10.2%。首先，将钨合金表面抛光，并在光学显微镜下观察，其微观组织结构如图1（a）所示。灰色部分是近似圆形的钨颗粒，在粉末冶金过程中会稍微发生变形，而黑色部分为粘结相。钨颗粒被粘结相包围，二者之间存在明显的界面。之后，统计钨颗粒尺寸的分布特征，其直径主要分布在10～60 [μm]，并近似服从正态分布，均值（[μ]）为28.5 [μm]，标准差（[σ]）为10.553，统计数目（[N]）为700，如图1（b）所示。

2 钨合金微观结构模型建立过程

钨合金两相微观结构模型的建立过程主要分三个步骤，分别是颗粒挤压模型的建立、轮廓重建与几何修复、内聚力单元的插入。

2.1 颗粒挤压模型

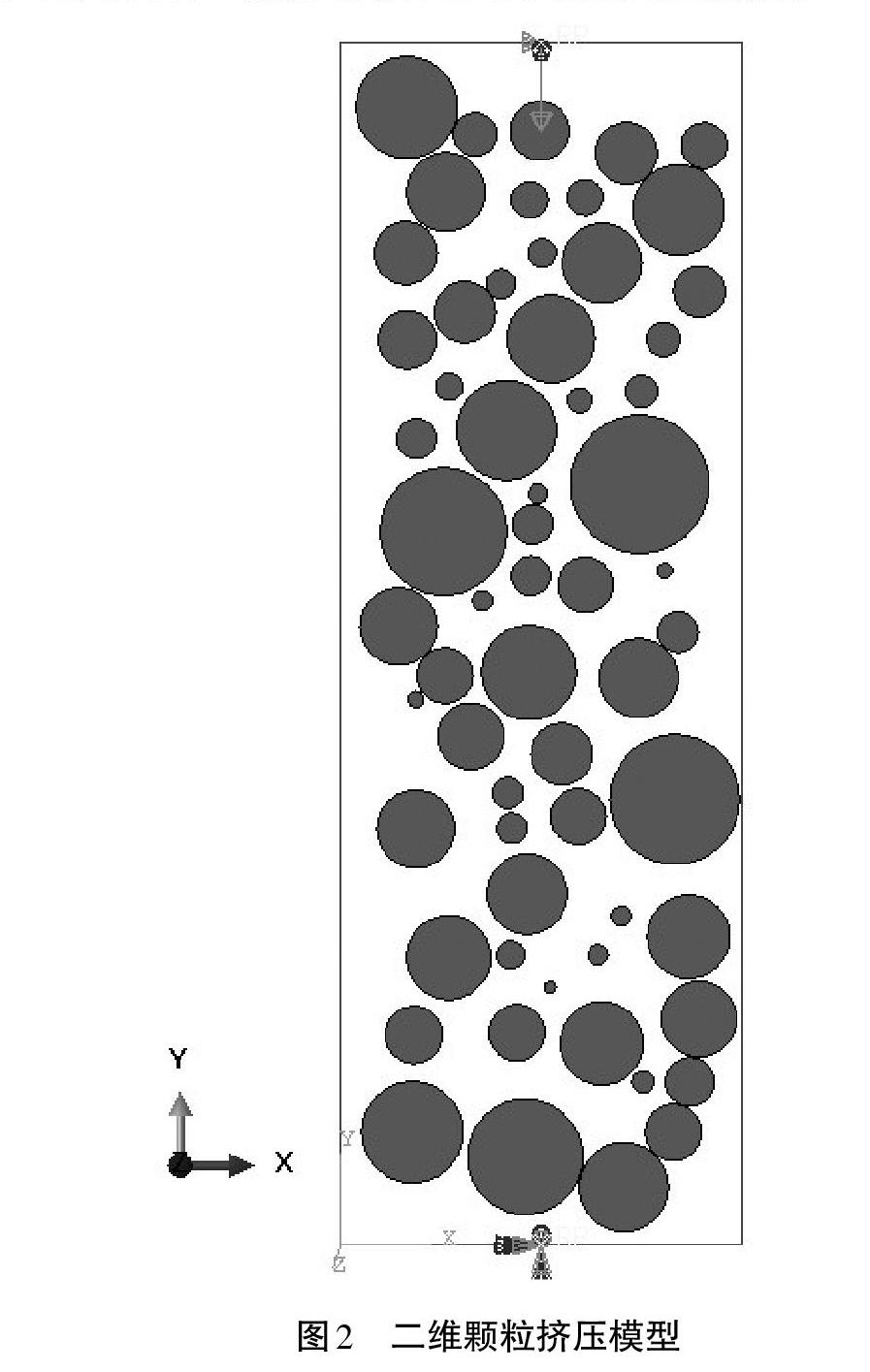
根据钨合金粉末冶金的制备过程，研究人员在ABAQUS软件中建立了二维颗粒挤压模型，如图2所示。首先，根据颗粒分布特征，利用RSA加密算法在MATLAB软件中生成初始颗粒。颗粒的位置（用[x]和[y]坐标表示）是在指定区域中随机生成的，颗粒的尺寸（用[d]表示）也是随机生成的，且服从上述提到的正态分布。因此，每次生成的颗粒都可以用一组随机数（[x]、[y]和[d]）表示。如果当前生成的颗粒不与之前已生成的颗粒重叠（两个颗粒之间的距离大于它们的半径和），则记下该颗粒的信息（[x]、[y]和[d]）。如果当前生成的颗粒与已生成的颗粒重叠，则将其舍弃，并重新生成颗粒，再做判断，直到所有颗粒的体积分数达到要求。随后，输出所有颗粒的信息，编写Python脚本程序将颗粒信息输入ABAQUS软件中。接着，在ABAQUS软件中创建一个可以包含所有颗粒的四边形刚体，刚体的上边界可以向下移动，以实现挤压过程，而其他边界则完全固定。将每个颗粒设置为弹性体，并任意给定合理的弹性模量和泊松比。网格划分和接触设置都通过Python脚本实现。网格最小尺寸为0.001 mm，网格划分得越细，最终模型的轮廓越精确。颗粒之间、颗粒与刚性边界之间都设置相互接触。

随着上边界的连续向下移动，颗粒逐渐被挤压变形，颗粒的体积分数逐渐上升。当所有颗粒的体积分数达到钨合金中钨颗粒真实的体积分数时，提取所有颗粒的轮廓，输出每个颗粒边界上所有的节点坐标。为了保证边界上的节点按照顺序逐个输出，在挤压模型运算之前，要将每个颗粒边界上所有的节点从小到大重新编号。

2.2 轮廓重建与几何修复

完成挤压模型后，依次输出变形后所有颗粒边界上的节点坐标，再编写Python脚本程序将其按顺序输入ABAQUS软件中，以完成建模。轮廓重建的模型如图3（a）所示。随后，创建一个可以包含所有变形颗粒的矩形实体，并对所有颗粒执行布尔运算，以获得粘结相的模型，如图3（b）所示。至此，钨合金的两相模型已初步建立。但是，该方法中颗粒的边界是由输入的节点依次连接形成的，由于计算机本身的数值误差，相邻颗粒之间可能会存在微小的间隙，这不利于后续的网格划分，并且会严重影响网格的质量。因此，在划分网格之前需要进行几何修复。

将上述的颗粒和粘结相模型保存为IGES文件格式，并将其导入Hypermesh软件中，使用其几何修复功能来清理重复的边和狭窄的边，并适当调整几个颗粒相交的狭小区域，以提高网格质量。然后，划分网格，尽管四边形单元的求解精度高于三角形单元，但在相邻颗粒的区域四边形单元网格质量比三角形单元差，因此使用三角形单元。接下来，为每个颗粒和粘结相创建单独的单元集，以便随后赋予材料属性。最后，将上述模型导出为INP文件格式，该文件类型可以直接通过ABAQUS软件读取。最终在ABAQUS软件中显示的网格模型如图4所示。

2.3 内聚力单元的插入

在获得了包含颗粒和粘结相的网格模型后，进一步考虑颗粒边界的存在，在颗粒-颗粒界面和颗粒-粘结相界面插入一层零厚度内聚力单元。ABAQUS软件可视化窗口不能直接生成零厚度的内聚力单元，因此要编写Python脚本来修改INP文件，实现内聚力单元的插入[4]。在INP文件中，要重点修改三个部分：节点信息、单元信息以及单元集信息。为了在边界上插入内聚力单元，首先要将边界上的节点分裂，边界上的节点在颗粒或粘结相集合内出现几次就需要分裂几次，然后用新分裂出的节点替换边界单元内原来的节点。最后，利用分裂出来的节点创建内聚力单元，如图5所示。

3 钨合金两相结构拉伸模拟

上文介绍了在ABAQUS软件中利用Python脚本程序建立钨合金的两相微观结构仿真模型，该模型包括了钨颗粒和粘结相，还考虑了颗粒界面的存在。接下来将利用该模型进行拉伸仿真，与准静态下钨合金的拉伸试验曲线进行对比，从而验证该模型的可靠性。

3.1 钨合金拉伸试验

根据《金属材料 拉伸试验 第1部分：室温试验方法》（GB/T 228.1—2010），将95W-3.5Ni-1.5Fe合金制备成哑铃形试样，其尺寸如图6所示，然后将试样装夹在万能试验机上进行试验，为了获得准确的应变，在试样中段使用引伸计测量其变形。试验过程中采用位移驱动的方式进行加载，加载速度为0.2 mm/min，当观测到试验曲线过了屈服点之后，取下引伸计继续加载，直到试样被拉断。之后，利用试验机的力传感器和引伸计，得到钨合金的准静态拉伸应力-应变曲线。

3.2 钨合金两相结构拉伸仿真模型

二维平面应变的钨合金两相结构拉伸模型如图7所示，在模型的左右边界施加一个沿[x]方向的位移（[Ux]），等于常数[C]，[y]方向的位移（[Uy]）为零。如上所述，该模型包括三部分：钨颗粒、粘结相和界面。为了简便起见，钨颗粒的材料属性选用纯钨的弹塑性材料参数，粘结相的材料属性选用铁的弹塑性材料参数，二者的材料参数均列于表2中，纯钨和铁的塑性本构模型如图8所示[5]。界面给定双线性内聚力本构模型，如图9所示（[δ0]表示损伤起始点的位移，[δf]表示完全失效点的位移），该模型主要包含三个參数，即断裂能量[Gc]、最大应力[t0]和内聚力刚度[k]，各参数取值如表3所示。需要说明的是，界面的内聚力模型参数目前没有直接的试验测定方法，是结合仿真与试验曲线试凑出来的。具体的方法是运用控制变量法，不断调整内聚力模型的参数，直到仿真得到的应力-应变曲线与试验接近。

3.3 内聚力参数对钨合金拉伸性质的影响

在以上拉伸仿真中，试样的等效应力可以取右边界上所有节点沿[x]方向的应力的平均值，等效应变为试样的整体应变。等效应力和等效应变的计算公式为：

式中：[σ]为等效应力;[ε]为等效应变;[N0]为试样右边界上的节点数目;[σxx]为节点沿[x]方向的应力;[Ux]为右边界沿[x]方向的位移;[L0]为试样沿[x]方向的初始长度;[i]为非零自然数。

3.3.1 模型尺寸比对拉伸仿真结果的影响。模型的尺寸比（[Φ]）定义为模型整体尺寸与平均颗粒半径的比值。对于一个非均质的模型，其尺寸比应该足够大才能够包含足够多的微结构，模型才具有代表性，同时其尺寸比也应该足够小，才能节省计算成本[6]。因此，确定钨合金两相结构模型的尺寸比是有必要的。本研究保证平均颗粒尺寸不变，通过改变模型的整体尺寸来得到不同尺寸比的模型，如图10所示，三个模型的尺寸比分别为10、15和20。

三个不同尺寸比仿真模型的拉伸应力-应变曲线与试验曲线的对比结果如图11所示。从图中可以看出，当尺寸比为10时，仿真的应力-应变曲线与试验曲线保持一致的趋势，但是还存在一定的差异，说明该尺寸比下的模型代表性不足;而当尺寸比为15或20时，仿真曲线与试验曲线基本重合，因此可以说明尺寸比为15或20的仿真模型具有足够的代表性。为了方便研究，以下的仿真都采用尺寸比为20的模型。

3.3.2 内聚力刚度对拉伸仿真曲线的影响。对于内聚力单元刚度的选择，许多学者提出了不同的方法。DAUDEVILLE等根据界面厚度和弹性模量确定了内聚力刚度[7]。ZOU等根据经验，提出内聚力刚度值为单位长度界面强度值的104～107倍[8]。内聚力单元刚度应足够大，以提供合理的刚度，但也应足够小，以减少数值问题带来的风险。TURON等指出，内聚力刚度在大于材料弹性模量的50倍时，数值计算的结果对于大多数问题能够保证足够的精确性[9]。本文中，内聚力单元的刚度从1×105 N/mm3增加到5×107 N/mm3，而最大应力和断裂能量分别为520 MPa、55 N/mm，保持不变。仿真曲线与试验曲线的对比结果如图12（a）所示。当内聚力单元的刚度较小（1×105 N/mm3和1×106 N/mm3）时，内聚力单元不能为整体的模型提供足够的刚度，在拉伸过程中迅速发生损伤，导致拉伸的应力-应变曲线与试验曲线有很大误差;当内聚力单元刚度增加到1×107 N/mm3时，内聚力单元已经能够为整体的模型提供一定刚度，仿真的应力-应变曲线能够出现弹性-屈服-塑性阶段，但与试验曲线仍存在一定误差，表现为弹性阶段上升的斜率偏低，屈服后的塑性阶段应力值整体偏低;当内聚力单元刚度继续增加到5×107 N/mm3时，仿真曲线与试验曲线基本重合。因此，内聚力单元的刚度选择5×107 N/mm3比较合理，该值也符合TURON等给定的内聚力刚度确定方法，即大于50倍的弹性模量[9]。

3.3.3 最大应力对仿真应力-应变曲线的影响。最大应力反映了颗粒界面的连接强度，已经有研究表明，界面强度对钨合金的拉伸性能有很大的影响，较低的界面强度导致钨合金在拉伸过程中沿界面断裂，从而表现出较低的屈服强度和极限强度[10]。本文中，最大应力选择为400 MPa、520 MPa、600 MPa，内聚力单元刚度为5×107 N/mm3，断裂能量为55 N/mm。仿真曲线与试验曲线的对比结果如图12（b）所示，当最大应力为520 MPa时，弹性和塑性阶段模拟的应力-应变曲线与试验结果吻合较好。当最大应力增大或减小时，仿真的应力-应变曲线弹性阶段上升的斜率几乎没有变化，而屈服强度相应增大或减小，这与已有的结论保持良好的一致性。

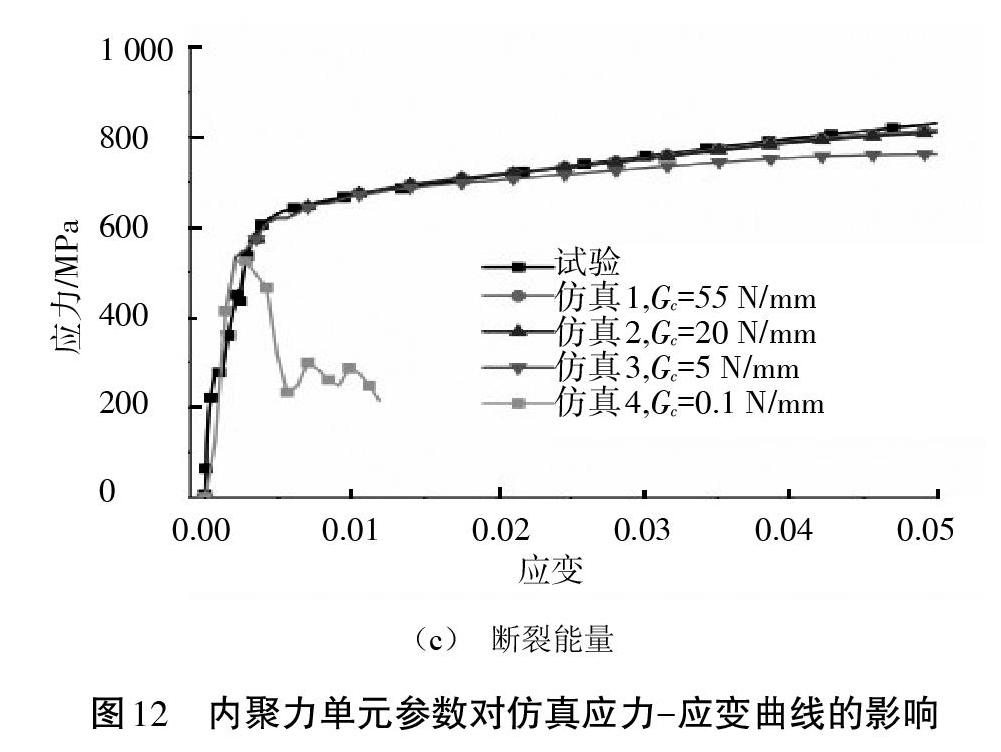
3.3.4 断裂能量对拉伸仿真应力-应变曲线的影响。断裂能量从0.1 N/mm增大到55 N/mm，内聚力刚度为5×107 N/mm3，最大应力为520 MPa。仿真结果如图12（c）所示，从曲线中可以看出，当断裂能量足够大时（5N/mm、20 N/mm、55 N/mm），该值对仿真的应力-应变曲线影响很小，几乎不影响弹性阶段上升的斜率，稍微影响屈服后的塑性阶段，断裂能量越小，塑性阶段下降越快。而当断裂能量减小到一定程度（0.1 N/mm）时，仿真的应力-应变曲线发生很大的变化，在经历了一定的上升阶段后，曲线迅速下降，这是由于给定的断裂能量太小导致内聚力单元在拉伸过程中完全失效，从而使拉伸应力-应变曲线出现骤降现象。

4 结论

根据95W-3.5Ni-1.5Fe合金粉末冶金的加工工艺，本文提出了一种基于颗粒挤压的两相结构建模方法。首先根据钨合金的实际颗粒分布特征，利用RSA算法在MATLAB软件中生成了初始颗粒构型，然后将所有颗粒信息输出到ABAQUS软件中建立一个颗粒挤压模型。随着挤压过程的不断进行，模型模拟的颗粒体积比逐渐上升，当其达到真实的颗粒体积比时，将所有颗粒轮廓输出，并编写Python脚本程序将颗粒轮廓输入到ABAQUS软件中完成轮廓重建，随后运用布尔运算生成粘结相，最后在颗粒与粘结相相交的区域插入内聚力单元，以模拟颗粒界面的作用。上述模型被应用于拉伸仿真，本研究结合准静态下95W-3.5Ni-1.5Fe合金的拉伸曲线确定了内聚力单元的材料参数，最后分析了内聚力单元参数对拉伸曲线的影响。

研究表明，本文基于颗粒挤压的方法建立的95W-3.5Ni-1.5Fe合金两相细观结构仿真模型是可行的，该模型考虑了95W-3.5Ni-1.5Fe合金中钨颗粒、粘结相以及颗粒界面，近似还原了95W-3.5Ni-1.5Fe合金的真實结构。根据仿真与试验，本文得到了95W-3.5Ni-1.5Fe合金颗粒界面的内聚力单元参数。其中，内聚力单元的刚度主要影响拉伸应力-应变曲线弹性段的斜率，单元刚度越低，曲线弹性段的斜率就越低;最大应力主要影响拉伸应力-应变曲线的屈服点，对弹性段的斜率几乎没有影响;断裂能量在一定范围内对拉伸-应力-应变曲线的影响很小，且主要影响塑性阶段。

参考文献：

[1]罗荣梅.一种95W细晶钨合金动态力学性能[J].辽宁化工，2015（7）：776-778.

[2]KIRAN U R，KHAPLE S K，SANKARANARAYANA M，et al.Effect of swaging and aging heat treatment on microstructure and mechanical properties of tungsten heavy alloy[J].Materials Today：Proceedings，2018（2）：3914-3918.

[3]SATYANARAYANA P V，BLESSTO B，SOKKALINGAM R，et al.Effect of Fe Addition to Binder Phase on Mechanical Properties of Tungsten Heavy Alloy[J].Transactions of the Indian Institute of Metals，2019（4）：1-9.

[4]王鷹宇.Abaqus分析用户手册[M].北京：机械工业出版社，2018：60-62.

[5]刘筱玲.钨合金材料宏微观性能分析及动态性能测试研究[D].成都：西南交通大学， 2008：20-22.

[6]SAVVAS D，STEFANOU G，PAPADRAKAKIS M.Determination of RVE size for random composites with local volume fraction variation[J].Computer Methods in Applied Mechanics and Engineering，2016（305）：340-358.

[7]DAUDEVILLE L，ALLIX O，LADEVEZE P.Delamination analysis by damage mechanics：Some applications[J].Composites Engineering，1995（1）：17-24.

[8]ZOU Z，REID S R，LI S.Modelling Interlaminar and Intralaminar Damage in Filament-Wound Pipes under Quasi-Static Indentation[J].Journal of Composite Materials，2002（4）：477-499.

[9]TURON A，DAVILA C G，CAMANHO P P.An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models[J].Engineering Fracture Mechanics，2006（10）：1665-1682.

[10]SENTHILNATHAN N，ANNAMALAI A R，VENKATACHALAM G.Microstructure and mechanical properties of spark plasma sintered tungsten heavy alloys [J].Materials Science & Engineering A，2018（710）：66-73.