高维度集中空调系统优化控制模型及算法研究
王子轩,姚晔*,赵鹏生
(1-上海交通大学制冷与低温工程研究所,上海 200240;2-上海真聂思楼宇科技有限公司,上海 200331)
0 引言
低碳经济的发展对建筑节能提出了越来越高的要求。据统计,中央空调系统占建筑年平均能耗的50%[1]。集中式中央空调在公共建筑中应用普遍,其节能空间大,集成度高,测控模块完备,为优化控制提供了硬件支持,是空调节能的焦点。
许多学者在集中空调节能控制方面进行了研究。LIANG 等[2]建立了ARMAX 预测模型,并运用模型预测实时调整风阀开度,实现了空气处理设备(Air-handling Unit,AHU)层面的节能。MOSSOLLY 等[3]使用遗传算法对一个七区域的小型空调系统进行优化,实现了权衡能耗和空气质量的多目标优化。LI 等[4]考虑电价和热负荷等时变因素,优化了空调系统的经济性。蔡盼盼等[5]以一个空调系统实验台为对象,进行了低维度空调系统的建模和优化研究。AFROZ 等[6]将空调系统的建模方法分为白箱、灰箱和黑箱3 大类进行了综述性概括。GHAHRAMANI 等[7]对HVAC 系统进行了无模型控制的仿真研究。负荷预测和建模方面也有较多研究[8-12]。
相较于有模型控制,无模型控制由于需要通过试错进行启发性训练,从算法仿真到工程应用需要付出更多的稳定性的代价和训练时间。因此,本文从系统建模和模型求解角度进行研究。
高维度是集中空调系统优化控制的难点。建筑热负荷主要来自外墙传热、太阳辐射和人员设备散热[13],因此一栋建筑不同区域的热负荷具有差异性,而一栋公共建筑的众多区域往往由一套中央空调系统提供冷量,这在数学模型上反映为优化参数的高维度。因此,从整体的角度实时地为具有不同负荷特性的区域设定最优运行参数,是集中式空调系统节能运行的关键。当前的研究主要侧重于AHU和送风末端层面的控制,以及小型空调系统的整体优化;而关于大型集中空调系统对应的高维度优化运行问题,相关的建模和优化算法研究比较稀缺。
粒子群优化算法是一种广泛应用于函数优化的智能优化算法,然而其具有容易陷入局部最优解等不足。为此,本文提出了一种适合求解高维优化问题的随机增量式粒子群优化算法(Random Increment Particle Swarm Optimization,rPSO),并以上海市一栋公共建筑的集中空调风-水系统为案例,建立了以节能为目标的优化模型,以rPSO 为求解算法进行了多工况的仿真,以验证rPSO 的高维寻优性能和优化控制算法的节能潜力。
1 优化模型
1.1 研究对象
图1所示为某大型集中空调系统,该系统负责64 个空调区域。冷冻水由冷源系统(包括冷水机组、冷却水泵和冷却塔)产生并储存于蓄冷水罐中;在末端有用冷需求时,冷冻水泵组将冷冻水输送至64个AHU 中的空气-水换热器换热,待处理空气在AHU 风机驱动下通过AHU 中的空气-水换热器换热降温除湿后送入至空调区域。本文以风-水系统为优化对象,包括冷冻水泵组和64 个AHU。

图1 某集中空调系统
1.2 部件能耗模型
AHU 风机的能耗模型为:

式中,Pfan为AHU 风机单位功耗,kW;Ga为送风流量,m3/s;ai(i=1,2,3,4)为回归方程系数,根据AHU 厂家提供的标准工况下的测试数据辨识;βfan为校正系数。除风量外,泵与风机功耗还与压力损失有关[14],βfan根据现场测试数据辨识。由于室内通风要求,以及散流器对送风流场均匀性的要求,送风风量一般不小于最大风量的20%~40%[15],研究对象为通风要求较高的公共空间,取ffan=40%,故送风流量有上下限GaMax和ffanGaMax。
冷冻水泵能耗由式(2)计算得到:

式中,Ppump为水泵单位功耗,kW;Gw为冷冻水流量,kg/s;bi(i=1,2,3,4)为回归方程系数;βpump为校正系数。由于电机转速限制,水泵的工作流量有上下限GwMin和GwMax。
冷冻水泵组的能耗由式(3)~式(5)计算得到:
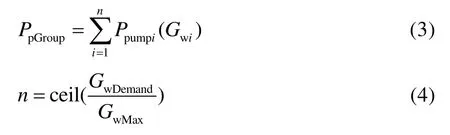

研究对象泵组由同型号水泵组成,最大质量为流量400 t/h(GwMax),最小流量为100 t/h。计算冷冻水总流量GwDemand后,各水泵间采用平均分配策略,计算水泵开机台数n(ceil 函数的含义是向上取整),最终结合式(2)计算泵组总能耗PpGroup。水泵的小流量开机是一种低效状态,系统整体优化需要选择最优开机台数。
AHU 表冷器的换热模型见式(6)和式(7)[16]:
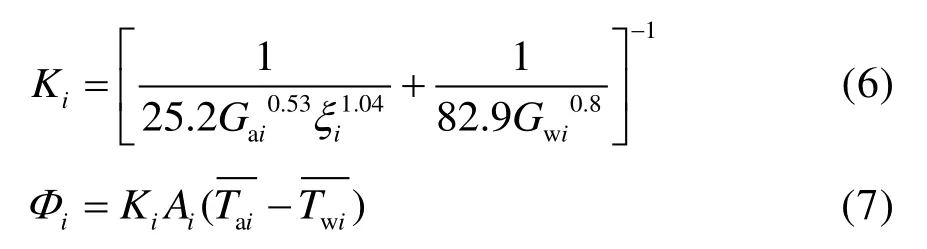
式中,i为系统中的第i台AHU,i为正整数;Ki为传热系数,W/(m2·K);Φi为换热量,W;ξi为空气测析湿因子;为表冷器空气进出口温度的算术平均值,K;为表冷器冷冻水进出口温度的算术平均值,K;Ai为空气侧换热面积,m2。
1.3 系统优化控制模型
AHU 与泵组的功耗具有耦合关系,以HVAC系统功耗最小为优化目标,建立控制优化模型,其对应的最优化问题的数学描述为:

式中,NAHU为系统中AHU 的数量,i为AHU 的编号;Psys为系统总功耗,kW;为一个维度NAHU的序列,是NAHU个AHU 送风温度TaLi的一个可行解。向模型输入,可根据式(1)和式(7)即能力守恒方程计算每个AHU 风机的送风流量和需要的冷冻水流量,最终根据式(3)和式(8)求出风-水系统总功耗Psys。Psys在最优化问题中称为适应度,使用优化算法求解出一个使适应度最小的称为最优解。约束条件要求所有水泵和AHU 风机的流量不得超过上下限,为刚约束,换热量Φ(TaLi)尽可能满足负荷,差值不超过正负偏差变量d+,d-为软约束。
图2所示为优化控制模型的输入输出及其时间关系,其符号说明见表1。在第k时刻测量输入参数,运行优化程序计算第k+1 时刻的优化运行参数,在第k+1 时刻将参数输入硬件系统执行。其中,n维序列用于记录n个同类型设备的参数;测量k时刻AHU 冷冻水进出口温度的温差计算,由于测量时刻k与执行时刻k+1 间隔短,认为。
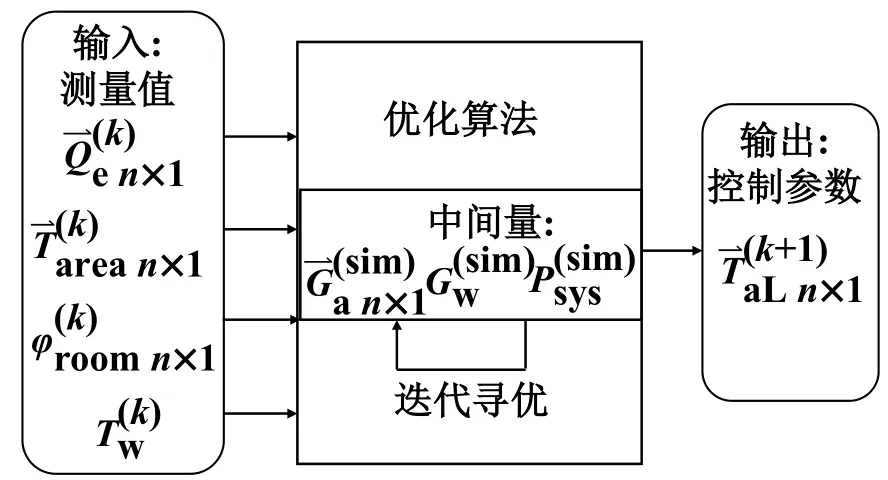
图2 优化控制模型

表1 优化控制模型框图中的符号说明
优化模型需要通过粒子群优化算法(Increment Particle Swarm Optimization,PSO)迭代求解,每次迭代调用一次系统能耗模型,每次优化模型求解的用时约为topt=NiterNswarmtmodel,其中Niter为PSO 迭代次数,Nswarm为PSO 粒子数,tmodel为求解一次能耗模型的用时。
在对优化模型编程求解时,考虑到求解时间,对系统能耗模型进行了部分简化,不影响问题的本质,简化如下:1)式(6)~式(7)在K变化不大的情况下,将K设为经验常数,降低优化计算中迭代求解K付出的代价;需要使用精确值时,采用二分法迭代计算;式(6)~式(7)需要使用传热系数K,在K变化不大时,将K看作常数;2)对于并联系统,认为AHU 冷冻水入口温度等于总管供水温度。
2 优化算法
2.1 粒子群优化算法
粒子群算法(PSO)于1995年由KENNEDY等[17]首次提出,许多学者后续提出了多种改进算法,以提升其寻优性能和通用性,因此目前PSO 的具体实现形式是多样化的,SHI 等[18]和CLERC[19]提出了如下形式的PSO 算法:
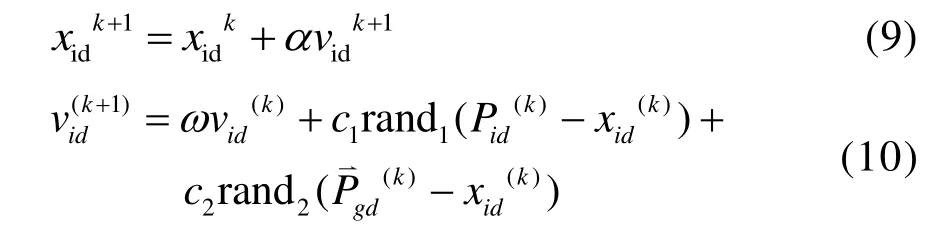
式(9)和式(10)形式的PSO 方程应用广泛,很多学者将其看作基本粒子群算法(bPSO)[20]。
2.2 随机增量粒子群算法
高维函数优化常常面临多峰搜索问题,PSO 在求解这类问题时,容易出现“早熟收敛”,陷入局部最优解;同时,PSO 的寻优性能受到模型参数的影响。
本文为增强算法的全局寻优能力,从加宽搜索角度出发,提出了一种用于高维函数优化的改进型粒子群优化算法,即随机增量粒子群算法(rPSO)。其迭代流程与基本PSO 类似,如图3所示。多次实验发现,对于本问题的寻优在200 代之后适应度下降不再明显,本文以300 代作为rPSO 收敛条件。

图3 rPSO 迭代寻优流程
rPSO 的改进体现在粒子速度的更新方程,其更新思想是:首先根据速度惯性、与个体历史最优位置的距离、与种群历史最优位置的距离3 项,确定一个向量,再将其归一化,得到一个方向向量仅由1、-1、0 三种元素构成),确定粒子速度更新的方向;最后,对每一维乘以一个与该维度取值范围相关的随机增量,从而确定粒子速度更新的增量,同时用step 因子控制速度随机增量的步长范围,使粒子移动步长适中。随机性保证了rPSO 粒子搜索中有更宽的搜索方向角,适中的步长保证了优化算法的收敛性,这些特性提升了PSO 高维寻优中找到全局最优解的能力。rPSO 每轮迭代的方程如下,其中式(11)为位置更新方程,式(12)为速度更新的标量形式,式(13)为向量形式。

式中,ω、c1和c2分别为惯性因子、自我学习因子和种群学习因子,取值范围一般取[0,2],step 因子一般取0.2,下标id为第i个粒子的第d维,上标k表示第k次迭代,分别为粒子的位置和搜索速度,也对应优化变量的取值,randj(j=1,2,3)是一个服从U(0,1)平均分布的随机数,对于每个粒子每一维度randj均重新随机生成;适应度是目标函数的值,为直到第k次迭代第i个粒子找到的适应度最低的位置,为直到第k次迭代所有粒子找到的适应度最低的位置。粒子位置更新要判断新位置是否超出取值范围的上下界xdHigh、xdLow,xLimitd=xdHigh-xdLow是第d维区间长度。
2.3 性能对比
使用bPSO、rPSO 分别对64 个AHU(对应64个区域)的大型集中空调优化运行问题进行仿真实验。每个区域的负荷设置为AHU 最大冷量的50%,粒子数为100,迭代次数为300,rPSO 的step 因子取0.2,bPSO 的α取1,ω,c1,c2取两组见表3。每组实验中rPSO 和bPSO 分别求解50 次,寻优结果和统计见图4 和表2。
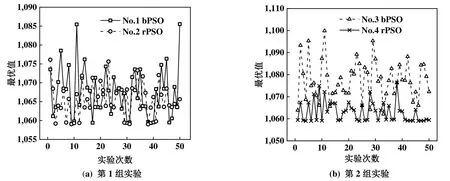
图4 rPSO-bPSO 寻优能力对比

表2 rPSO-bPSO 寻优实验统计
由表2 可知,rPSO 具有两点优势:1)rPSO 的寻优性能更稳定,由于粒子群算法是一种群体启发式寻优算法,其寻优结果具有一定随机性,对于存在众多局部最优解的高维优化问题,随机性更明显。对比第1 组~第4 组的最优值方差,发现rPSO求解方差明显小于bPSO,即rPSO寻优性能更稳定;2)rPSO 对模型参数的敏感性更低,调参更简单,工程实用性更强。对于rPSO,在第1 组和第3 组不同的模型参数下,寻优平均值和方差都相近;而对于bPSO,在第2 组和第4 组不同模型参数下,寻优平均值和方差相差很大,且第4 组寻优性能不 。
在工程中,优化问题是差异性的,选择模型参数的工作必不可少,rPSO 对模型参数的低敏感性使这部分工作更加便捷和省时;另外稳定性是算法在工程应用中的考量因素。因此,rPSO 更好的寻优稳定性和调参便利性,使其在工程应用具有更好的应用前景。
3 优化运行仿真分析
根据现场调研,目前许多公共建筑的集中空调系统仍采用定送风温度的传统运行模式,送风温度一般为18 ℃或19 ℃。图1所示系统的无末端风阀,传统模式下,通过单独调节风机风量或单独调节水阀开度控制室温,即中高负荷,AHU 采用设计送风温度送风,送风温度恒定,通过PID 调节风量来控制供冷量,保持室温稳定;低负荷下,AHU 风量已达到最低限时,风机保持最低转速,通过PID 控制水阀来控制供冷量,保持室温稳定。这种控制策略的优点是,由于PID 适合单输入单输出控制,定送风温度可以保证风量PID 控制的稳定性;但是系统此时的运行参数非最优,存在能源浪费现象。
优化控制可以在保证室温稳定的前提下,实现系统的节能,主要通过两步算法实现:1)根据负荷情况,动态调整各AHU 的送风温度,达到系统能耗最优;2)用模型预测控制替换传统策略中风量控制的简单PID 算法。本文的优化模型求输出的最优送风温度后,再将其作为模型预测控制的输入,用于风量控制,模型预测控制在风量控制中已有成熟的应用[2]。
图5 对比了在不同的平均负荷率下,优化控制相对传统的定风量送风模式的节能潜力。仿真分为第1 组和第2 组,其平均负荷率相同但局部负荷分布不同,64 个空调区域的局部负荷分布服从截取在[0.3,1]上的正态分布X~N(μ,s),s为方差,对于第1 组和第2 组分别为0.05 和0.15,μ为负荷率均值,μ∈[30%,100%](负荷率低于30%时,系统不再定送风温度运行,不进行能效对比)。

图5 优化控制-定温送风模式功耗对比
分析图5 发现:1)优化控制在不同的负荷分布下节能效果不同,整体上,随系统整体负荷率的升高而升高;2)中负荷段,第2 组的节能潜力更大,即此时,优化控制对负荷分布不均匀程度大的系统有更大的节能潜力;3)由于正态分布的负荷不完全由均值μ确定,还具有一定随机性,因此功耗不随μ完全单调递增;4)优化控制的节能效果明显,对于第1 组,节能率最高为16.85%,平均为13.18%,对于第2 组,节能率最高为17.04%,平均为13.45%。
图6所示为第1 组和第2 组64 个区域负荷分布的差异性,可知第2 组负荷分布的差异更大。

图6 各区域的负荷分布
4 结论
本文提出一种高维度集中空调系统的优化控制模型及求解算法,即随机增量粒子群优化算法(rPSO)。以一个64 区域的集中空调系统为案例进行建模和多工况优化仿真,得出如下结论:
1)与基本粒子群算法bPSO 对比,rPSO 求解稳定性更好,模型参数选取更便利,在工程应用中实用性更强;
2)在不同负荷下,优化控制带来的节能率不同,在负荷率均值为30%~100%的中高负荷段,对于第2 组不同的负荷分布,优化控制相对于18 ℃定送风温度模式,平均节能率分别为13.18%和13.45%;
3)优化模型对送风温度进行动态调整,对急剧变大(或变小)的负荷具有更好的响应能力;
4)对不同类型的集中空调系统,可采用与本文不同的建模方法来建立优化模型,但本文的优化算法对于这些模型的求解具有普遍使用性。

