直流系统机电暂态通用化建模技术

赵利刚，洪潮，甄鸿越，周挺辉，王长香，黄冠标，张野

(直流输电技术国家重点实验室(南方电网科学研究院)，广州510663)

0 引言

直流输电技术由于其线路走廊窄、输送容量大、输送距离不受限制等优点，在电能的远距离大容量输送方面得到了广泛应用。目前，我国已投运的两端直流输电系统超过20回，包括两端常规直流、两端柔性直流、背靠背常规直流、背靠背柔性直流等多种形式；南澳三端柔性直流输电工程、舟山五端柔性直流工程均已投产运行。2020年，张北柔性直流电网示范工程和昆柳龙±800 kV特高压多端混合直流输电工程正式竣工投产。直流输电技术正在经历从两端到多端再到直流电网的发展过程[1]。

在现有的商业化交直流大电网安全稳定计算分析软件中，基本涵盖两端的常规直流或者多端的柔性直流输电系统的建模仿真，但是对于混合直流以及直流电网，已有商业化软件较少涉及。文献[2]分析了VSC的稳态模型及其控制方式，推导了含VSC直流电网的交直流网络稳态潮流模型，提出了一种含VSC换流器的统一交直流网络潮流交替迭代方法；文献[2]更多地针对交直流电网的稳态分析方法，对于暂态仿真尚未涉及。文献[3]针对多端直流输电系统的机电暂态建模问题，构建了不同类型换流器和多端直流线路组成的多端直流网络的等值电路，提出了多端直流输电系统中不同类型换流器的控制方式以及各换流站间控制方式的协调机制，建立了多端直流输电系统机电暂态仿真通用模型；将直流输电系统的机电暂态建模从两端直流扩展到了多端及混合直流，尚未进一步扩展到直流电网。文献[5]介绍了直流电网建模仿真的最新发展，总结了适用于直流电网的设备模型和仿真方法，提出了直流电网建模和仿真技术的挑战；该文献更多地关注直流电网的电磁暂态建模相关技术总结，对于机电暂态仿真涉及较少。上述文献从稳态潮流分析到暂态的机电或电磁暂态仿真等方面对直流电网的建模方法开展了相关研究，取得了丰富的研究成果，但是对于交直流大电网机电暂态仿真中含直流电网在内的多类型直流输电系统进行统一建模、提高仿真模型的通用性等方面涉及不多，因此有必要在此方面继续开展相关研究。

本文将交直流大电网机电暂态仿真中直流输电系统建模由嵌入交流系统的元件扩展到直流网络的维度，将电力系统分为交流网络和直流网络，交流网络和直流网络分别统一求解，交直流网络在换流母线处进行信息交互。文章将重点关注直流网络方程的建立及求解，提出换流器及其控制系统、直流线路等的建模方法，并通过算例系统对所提出方法进行仿真计算，验证其有效性和准确性。

1 直流网络建模的整体思路

传统交流电网由发电机、输电网络和用电负荷等组成。在其机电暂态仿真中，一般采用基于基尔霍夫定律的节点电压方程描述交流网络，将输电网络描述为节点导纳矩阵，将发电机和用电负荷等描述为节点注入电流或者导纳矩阵与注入电流的组合。在节点注入电流已知的情况下，可以根据节点电压方程求解得到各个节点电压，进而求得母线功率、线路功率和电流等各运行量。

在直流输电系统的类型及数量较少时，可以将直流输电系统作为嵌入交流系统的一个元件，对每个元件采用特定的模型进行模拟，比如两端常规直流、两端柔性直流、多端柔性直流等，建模及应用的复杂程度尚可接受。但是随着直流输电系统类型的不断增多，比如混合直流、多端直流、直流电网等的不断出现，如继续采用对单个直流输电类型进行特定建模的方法仿真软件中将出现很多个不同类型的直流系统模型，模型提供者的建模复杂程度不断提高，模型应用者的应用便利程度不断降低，该方法已不能适应直流输电系统的快速发展。

直流系统全电磁暂态仿真可以准确地模拟直流输电系统的动态响应，也能够适应各种不同类型的直流输电形式，但现阶段全电磁暂态仿真技术的仿真规模和计算速度尚难以满足大规模电网的仿真需求。因此，本文提出一种直流系统通用化建模方法，对不同类型直流输电系统的适应性更强、通用化程度更高，满足大规模交直流电网的大批量安全稳定计算分析需求。

直流网络的通用化建模技术将交流电网的模拟方法应用于直流系统。换流器对应交流电网中的发电机，直流线路对应交流电网中的线路/变压器等，直流负荷对应交流电网中的用电负荷，形成直流网络的节点电压方程，将全部直流系统作为一个网络统一求解，通过换流器与交流系统交互。此处的全部直流系统可以是一个相互联系的直流电网，也可以是多个互不联系的两端常规直流、两端柔性直流、两端混合直流、多端常规直流、多端柔性直流、多端混合直流以及直流电网的组合。

直流网络通用化建模的直流节点电压方程如式(1)所示。

YdcUdc=Idc

(1)

式中：Ydc为直流网络的节点电导矩阵，为n×n维的实数矩阵；Udc为所有直流节点的直流电压向量；Idc为所有直流节点的注入直流电流向量，Udc和Idc均为n×1维的实数列向量；n为直流节点数量。Ydc、Udc和Idc的形成方法将在后续作详细说明。求解式(1)得到直流节点电压向量后，即可求得直流网络内的换流器注入功率和电流、线路功率和电流等各变量。

需要说明的是，在采用基于直流节点电压方程的通用化建模方式后，也可以方便地将交流系统中网络故障的处理方法应用于直流网络中，可以通过对直流节点电导矩阵中自电导和互电导的修改来模拟直流系统内部的短路或断路故障，例如可以通过在某个节点的自电导中加上一个大电导值来模拟该节点短路。

在交直流大电网的机电暂态仿真中，交流网络一般采用0.01 s的计算步长，直流网络需采用更小的计算步长，一般取交流步长的1/20[3]。交直流系统通过交替求解完成交直流网络的完整求解过程，直流网络与交流网络的信息交互通过换流母线进行。交流网络将换流母线交流电压幅值和相角信息传递至直流网络；直流网络计算完成后，将换流站有功功率和无功功率传递至交流网络，因在一个交流步长内直流系统可能计算多步，直流系统传递至交流系统的有功和无功功率值取一个交流步长内多个计算步长的平均值，计算方法如式(2)所示。

(2)

式中：P、Q分别为交流系统计算时直流系统传递给交流系统的有功功率和无功功率；n为交流步长与直流步长的比值；Pi、Qi为每个直流步长计算得到的直流系统递至交流系统的有功和无功功率值。

经过大量实际电网系统的仿真验证，交替求解方法可以较准确地模拟交直流系统的动态响应，其交替误差在可接受的范围内，同时较大幅度地降低了仿真算法实现的难度。交替求解过程如图1所示。

图1 交直流网络求解示意图Fig.1 Schematic diagram of AC and DC network solution

除上述的直流网络节点电压方程外，直流系统的求解还包括换流器控制系统，因为直流输电系统采用较小的计算步长，同时考虑到程序实现的简单化，直流控制系统采用和直流网络交替求解的方式，为每一个直流系统计算步长。首先根据上一时步直流系统电压、电流、功率等运行量的数值，求解控制系统，得到控制系统的控制值，然后应用控制系统的控制值进行直流网络的求解，直流网络求解完成后，直流系统的一个时步计算结束，进入下一时刻。对于电网换相换流器(line commutated converter，LCC)，一般采用定功率、定直流电压、定直流电流、定熄弧角等控制方式，控制系统给出的控制值为晶闸管的触发角；对于电压源型换流器(voltage source converter，VSC)换流器，考虑一般采用直接电流控制，控制系统给出的控制值为dq坐标系的电流参考值，VSC换流器直接控制内环电流控制器，其响应速度小于机电暂态仿真的时间步长，在建模中一般忽略内环电流控制器，认为其可以实时跟踪dq轴电流的参考值。因此，在仿真中可以将控制系统给出的dq轴电流参考值直接作为dq轴电流实际值进行直流网络的计算。本文重点关注直流网络的统一建模求解，求解时认为控制系统给出的控制值已知，对于换流器控制系统的建模求解不再详细说明。

2 直流节点模型

根据是否与交流网络相连接，可以将直流节点分为换流节点和纯直流节点两类。换流节点通过换流器、换流变压器等与换流母线相连，从交流网络吸收有功功率或者向交流网络传递有功功率，换流节点根据换流阀类型的不同，又可以分为LCC换流节点和VSC换流节点。纯直流节点不与交流系统相连接，仅与其他直流节点连接，还可以连接直流负荷等。

2.1 LCC换流节点模型

LCC换流节点包括换流变压器、换流阀、平波电抗器、直流侧滤波器等，如图2所示。

图2 LCC换流节点示意图Fig.2 Schematic diagram of LCC converter node

换流变压器和换流阀采用准稳态模型描述，在交流电压、换流变变比、换流阀触发角已知的情况下，直流电压和交流电压、直流电流的关系如式(3)所示。

(3)

式中：Udc为直流电压；Idc为直流电流(方向为整流侧流向逆变侧)；Vt为换流母线的交流线电压有效值；nt为换流器桥数；kt为变压器变比；Xc=ωLc， 为变压器等效电抗；θ为换流器的控制角，对于整流器，为触发角，对于逆变器，则为关断角。

对式(3)进行变换，可以得到式(4)。

(4)

从式(4)可以看出，换流变压器和换流阀准稳态模型可以等效为电流源和电阻的并联。

对直流平波电抗器采用电感进行模拟，以电流流向直流线路为正方向，模型如式(5)所示。

(5)

采用隐式梯形积分法进行差分，得到平波电抗器的模型如式(6)所示。

(6)

式中：Udc1为平波电抗器换流阀侧的直流电压；Udc为平波电抗器直流线路侧的直流电压；Idc为平波电抗器上流过的直流电流；h为直流系统仿真步长，L为平波电抗器电感。从式(6)可以看出，平波电抗器模型也可以等效为电流源和电阻的并联。

直流侧滤波器采用电容进行模拟，电流以流向直流线路为正，直流侧滤波器的模型如式(7)所示。

(7)

式中：Ic为直流侧滤波器上流过的电流；C为直流侧滤波器的电容值。

采用隐式梯形积分法进行差分，得到直流侧滤波器的模型如式(8)所示。

(8)

从式(8)可以看出，直流侧滤波器模型同样可以等效为电流源和电阻的并联。

根据式(5)—(7)，LCC换流节点可以表示为恒定电流源和等效电阻并联的形式，如图3所示。

图3 LCC换流节点模型图Fig.3 LCC converter node model diagram

对应到式(1)，LCC换流节点模型可以分别表示成为直流网络节点电导矩阵和注入直流电流向量的对应变量。假设LCC换流节点的节点编号为i，对应节点电导矩阵的元素如式(9)所示。

(9)

对应注入电流向量的元素如式(10)所示。

(10)

2.2 VSC换流节点模型

VSC换流节点包括换流变压器、换流阀、平波电抗器等，换流阀可以是两电平、三电平或者MMC换流阀，本文以MMC换流阀为例进行说明，其示意图如图4所示。

采用直接电流控制时，控制系统的输出为dq旋转坐标系下电流的交轴与直轴分量，此时换流阀与交流系统的交换功率如式(11)所示。

(11)

式中：Vcd、Vcq分别为换流母线电压的d轴分量和q轴分量；Isd、Isq分别为控制系统输出电流的d轴分量和q轴分量。

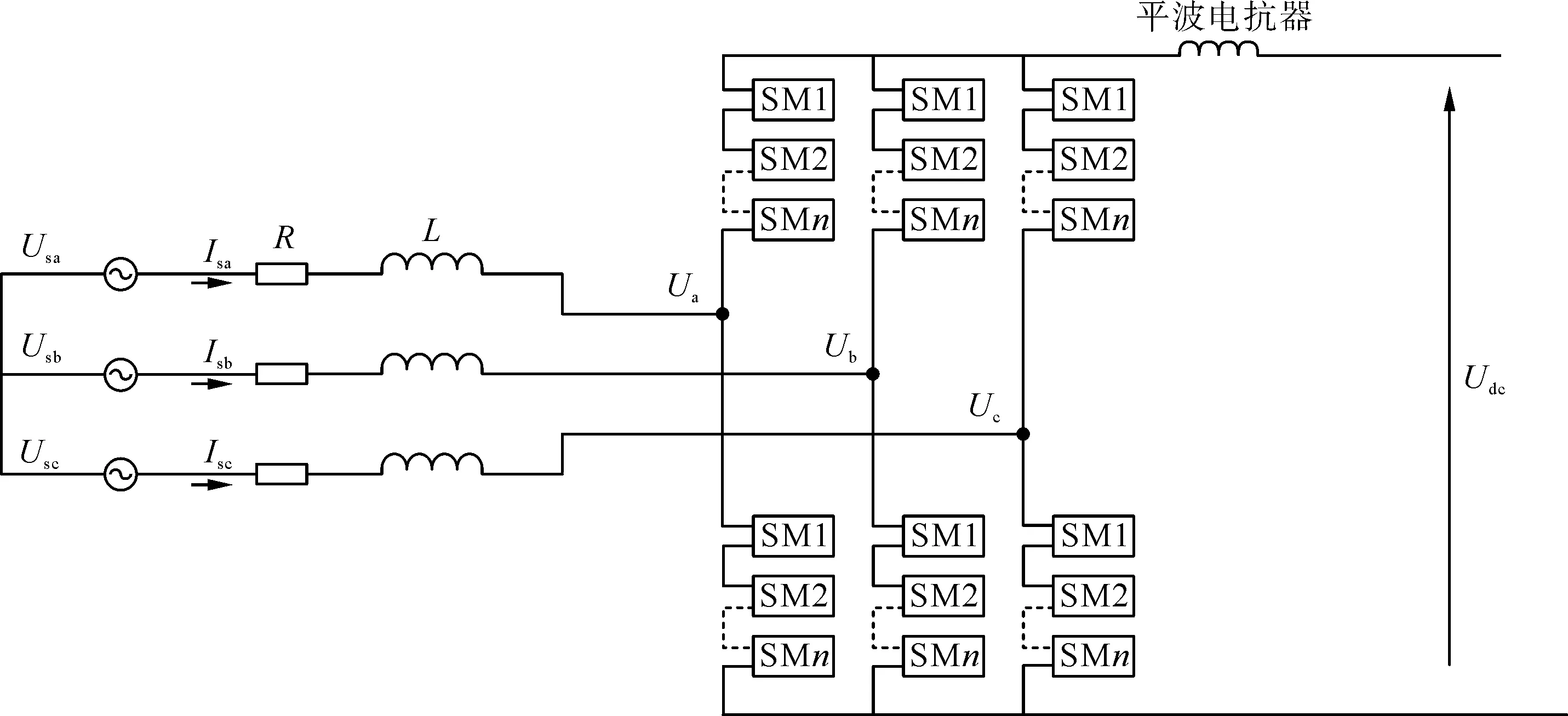
图4 VSC换流节点示意图Fig.4 Schematic diagram of VSC converter node

(12)

式中：Pdc为直流功率；kloss为换流阀的损耗系数，Udc为直流电压；C为换流器的等效电容；Id为等效电容换流阀侧的直流电流；Idc为等效电容平波电抗器侧的直流电流。

采用隐式梯形积分法对式(12)进行差分，得到VSC换流节点的模型如下。

(13)

直流平波电抗器模型可以采用与LCC换流节点模型中平波电抗器的处理相同，如式(5)—(6)所示，VSC换流器模型可以等效为图5所示的两个电流源和电阻并联然后串联的形式。

图5 VSC换流节点模型图Fig.5 VSC converter node model diagram

上述处理方式下平波电抗器两侧的直流电压均为未知量，直流电导矩阵和注入电流向量元素的形式将十分复杂。因为平波电抗器与直流线路相连，为了降低VSC换流节点模型的复杂程度，可以将平波电抗器电感并入所连直流线路的电感进行处理，VSC换流节点模型仅考虑换流阀。假设某纯直流节点的编号为j，VSC换流节点对应的节点电导矩阵元素如式(14)所示。

(14)

对应注入电流向量的元素如式(15)所示。

(15)

2.3 纯直流节点模型

对于接有直流负荷的纯直流节点，直流负荷模型可以参考交流网络中ZIP负荷模型，将负荷等效为恒定电阻、恒定电流或者恒定功率进行模拟，假设某纯直流节点的编号为k，恒定电阻负荷对应的节点电导矩阵元素如式(16)所示。

中国历史文化悠久，文化底蕴深厚，尤其是经典古诗文更是中华文化瑰宝，滋养着每一代人的健康成长。让小学生深入理解中华民族传统文化，培育学生的民族自豪感，有助于小学生人格的健全与发展，促进学生的可持续发展。语文知识重在积累，诵读经典可以在潜移默化中熏陶学生的心灵，提升学生的语文素养与知识应用能力。

Ydckk=Ydckk+1/R

(16)

式中R为负荷等效电阻。

恒定电流负荷对应的注入电流向量元素如式(17)所示。

Idck=Idck+Ikload

(17)

式中Ikload为负荷等效电流。

恒定功率负荷对应的注入电流向量元素如式(18)所示。

(18)

式中：Pkload为负荷等效功率；Udck为节点k的直流电压。

从式(15)、式(18)可以看出，如果存在VSC换流节点或恒功率直流负荷，直流节点电压方程式(1)为非线性方程组，需要采用牛顿法或其他迭代方法求解。

3 直流线路模型

直流线路采用π型等值电路模拟，考虑直流线路的电阻、电感和对地电容，示意图如图6所示。

图6 直流线路示意图(π型等值电路)Fig.6 Schematic diagram of DC line(π equivalent circuit)

其模型如式(19)所示。

(19)

式中：Udc1、Udc2为直流线路两端的直流电压；Rdc、Ldc、C1、C2为直流线路的电阻、电感和首末端电容；Idc、Ic1、Ic2分别为直流线路电流、首端电容流入和末端电容流向直流线路的电流。

将式(19)采用隐式梯形积分法进行差分，得到差分后的直流线路模型如式(20)所示。

(20)

根据式(20)，直流线路可以表示为恒定电流源和等效电阻并联的形式，如图7所示。

图7 直流线路模型图(恒定电流源与等效电阻并联)Fig.7 DC line model diagram(constant current source in parallel with equivalent resistance)

假设直流线路两端的直流节点编号为i、j，对应节点电导矩阵的元素如式(21)所示。

(21)

对应注入电流向量的元素如式(22)所示。

(22)

4 算例分析

基于电力系统计算分析软件DSP[8]开发完成本文所述的通用建模方法，建立图8所示的仿真算例验证本文所提方法的有效性。

图8 算例系统图Fig.8 Example system diagram

图8所示算例系统为含4个换流站的单极直流网络，直流电压为500 kV，每个换流站外接1个等值同步发电机，正常运行情况下，换流站1和换流站2为整流站，换流站3和换流站4为逆变站，初始潮流如图中所示。换流站及直流线路相关参数如表1—2所示。

为验证该直流网络在故障下的响应，在换流站2换流母线处设置三相接地短路故障，故障持续时间为0.1 s，直流网络的暂态响应过程如图9所示。

表1 算例系统换流站参数Tab.1 Example system parameters of converter stations

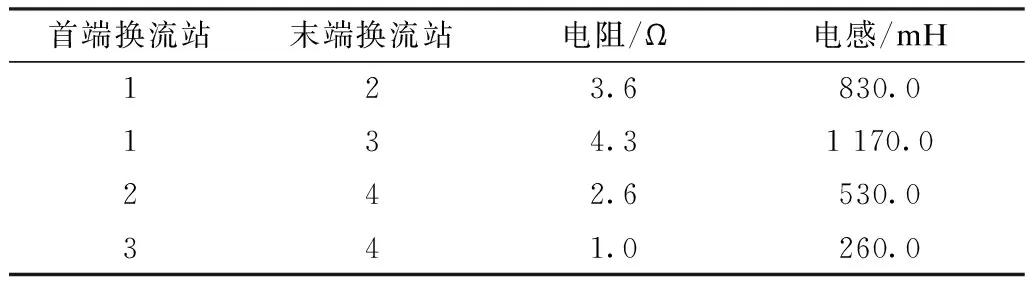
表2 算例系统直流线路参数Tab 2 Example system parameters of DC lines

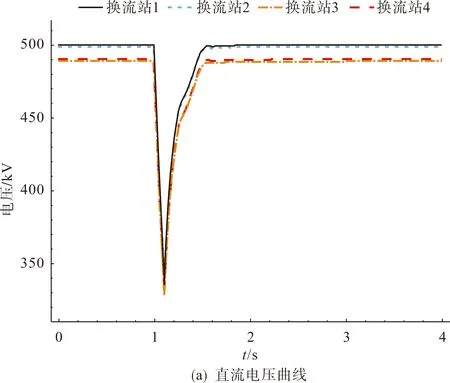
图9 算例系统结果曲线Fig.9 Result curve of example system

从图9可以看出，在换流站2发生三相短路后，换流站2的直流功率在故障期间降低至0，直流网络的注入功率减小，直流网络电压持续降低，为维持直流系统电压，换流站1的注入功率增大，换流站3和换流站4吸收的直流功率减小；在短路故障消失后，换流站2的直流功率迅速恢复，直流网络电压逐渐恢复，换流站1、换流站3、换流站4的直流功率也逐渐恢复至故障前数值。从仿真结果可以看出，所建立直流系统模型的故障响应特性符合预期变化规律，验证了本文所提建模方法的有效性。

5 结语

本文将交直流大电网的机电暂态仿真分为交流网络和直流网络，将全部直流输电系统作为直流网络进行统一建模仿真，交直流网络在换流母线处进行信息交互。详细说明了LCC换流节点、VSC换流节点、直流负荷、直流线路等的建模方法，在此基础上说明了直流网络节点电压方程的形成及求解方法，最后通过算例系统对所提出方法进行仿真计算，结果表明，所提方法能够有效适应多种不同类型的直流输电形式。