巷道围岩蝶形塑性区蝶叶方向性形成机制及工程应用

李 季，强旭博，马念杰，张荣光，李 博

(1.西安科技大学 能源学院，陕西 西安 710054; 2.中国矿业大学(北京) 能源与矿业学院，北京 100083)

一直以来，巷道矿压理论分析的基础是经典的支承压力理论，其核心是利用支承压力集中系数来反应围岩所处应力场的大小，但并未涉及围岩所处应力场的方向。由于该理论具有简单易行的优点，在巷道矿压理论分析中被广泛应用并发挥了重要的作用。然而，相关研究和实践表明[1]，深部巷道在受到大埋深和强采掘的影响下，其所处应力场会变得相对复杂，其复杂性不仅体现在应力场大小的增减，而且其应力场方向也会发生改变[2-3]，进而导致深部巷道出现一些新的巷道矿压现象，例如矩形巷道尖角处围岩变形破坏并非最严重、巷道围岩呈现非均匀变形破坏特征等[4-7]。众所周知，地下巷道围岩的变形破坏是由围岩产生的塑性区引起的，塑性区的形态和范围决定了围岩变形破坏的模式和程度，而塑性区的产生是围岩所处应力场和自身力学性质共同作用的结果。此时，采用经典支承压力理论进行分析时，便会忽视应力场方向对深部巷道围岩塑性区分布特征的影响，导致其无法很好地解释深部巷道出现的一些新的矿压现象。因此研究应力场方向对围岩变形破坏特征的影响对于深部巷道矿压理论分析具有重要的理论意义。

针对应力场方向对巷道围岩变形破坏的影响，国内外学者先后进行了有益地探索。最早关于应力方向对巷道稳定性的研究即为澳大利亚学者GALE W J提出的最大水平应力理论[8]，该理论认为巷道围岩的所受应力具有明显的方向性，且巷道顶底板破坏主要受水平应力影响，即巷道与水平应力的夹角越小，顶底板的稳定性越好;此后，众多学者以此为基础进一步研究了围岩应力方向与巷道轴向之间的关系对巷道围岩稳定性的影响，孙玉福[9]利用数值模拟得到围岩塑性区会随着巷道轴向与最大水平主应力间夹角的不同而发生改变，且夹角与巷道围岩稳定性有很大关系;朱志洁等[10]通过分析得出巷道围岩稳定性会随着最大水平主应力与巷道轴向间夹角的改变呈现复杂变化;高圣元等[11]通过研究发现背斜构造中巷道轴向布置角度会对围岩稳定性产生重要影响，夹角在60°附近时可降低围岩变形;赵亮等[12]研究发现巷道与最大水平主应力以一定角度斜交时，巷道顶底板的变形会偏向某一侧;高富强[13]认为最大水平主应力方向与巷道轴向的夹角越大时，巷道稳定性越差;赵龙[14]通过研究发现巷道轴线与最大主应力方向夹角在20°～70°时，对巷道围岩变形及破坏范围影响最为严重;田成东和白海波[15]认为巷道变形量会随着巷道轴向与最大水平应力间夹角的增大而增大。近年来，部分学者开始关注采动应力场方向对围岩变形破坏的影响，黄炳香等[16]通过研究发现在高地应力和强烈采动应力共同作用下，围岩行为迅速表现为复杂的非稳态、非线性特征;张文忠[17]利用数值模拟的方法研究了断层附近采动主应力方向偏转情况及断层面剪应力及剪应力增量的分布规律;周钢等[18]研究认为原岩地应力的最大主应力以铅垂应力为主，在采动过程中最大主应力方向与水平面夹角逐渐减小，且会严重影响巷道围岩稳定性;陈上元等[19]认为采动应力造成巷道围岩应力场的大小和方向发生改变，从而导致了巷道的非对称变形;王家臣等[20]采用理论分析、数值模拟及现场实测的方法研究了采动应力旋转角度对围岩稳定性的影响，采动应力旋转造成围岩承载能力降低，采动应力旋转角度愈大，围岩稳定性愈差。

以上研究分别从围岩应力方向与巷道轴向关系，采动应力场方向变化等方面入手，研究了围岩应力场方向与巷道布置的关系，并开始关注到采矿活动引起采场顶板岩层运动，会造成围岩所处应力场方向改变[16-18]，但并未涉及围岩应力场方向对塑性区形态影响的定量规律。因此，笔者以巷道蝶形破坏理论为基础，采用理论计算和数值模拟等方法，重点研究主应力方向对围岩蝶形塑性区形态的影响规律及蝶形塑性区蝶叶方向性的形成机制。

1 塑性区蝶叶形态表征

实际工程中，巷道所处的天然应力场并非均匀应力场，而是会因巷道埋深、地质构造作用等因素，水平应力与垂直应力存在大小差异(侧压系数≠1)，在受采掘扰动后，井下巷道围岩所处非静水压力场的非均匀程度将更加明显。因此，研究巷道处于这一非静水压力场中的围岩塑性区具有重要工程意义。关于非静水压力场下圆形巷道围岩塑性区问题，于学馥等[21]给出了双向非等压条件下圆孔周围的塑性区边界方程，此后由多位学者进行分析修正，后经马念杰等[22-23]详细推导后对圆形巷道围岩塑性区形态进行了归纳总结，提出了蝶形塑性区的概念，并对其形成机制及工程意义进行了详细阐述。虽然对非静水压力场中圆形巷道围岩塑性区边界方程的研究已经基本成熟，但对于塑性区蝶叶方向性及其工程应用的相关研究却鲜有涉及。

在非静水压力场中，巷道围岩塑性区形态将不再是经典的巷道围岩塑性区理论(如卡斯特奈公式和芬纳公式)所计算出的如圆形或椭圆形等均匀形态，而是呈轴对称的“蝶形”非均匀形态分布[22-23]，如图1所示。由图1可以看出，蝶形塑性区的边界轮廓分别在4个象限内凸出，将此凸出部分定义为塑性区蝶叶[24]。蝶叶最大半径即为塑性区的最大半径，其位置用极坐标(rmax，θmax)表示，a为圆形巷道的半径;P1为最大主应力;P3为最小主应力。

图1 蝶形塑性区形态示意Fig.1 Schematic diagram of butterfly plastic zone

同时根据笔者已有研究成果[25]表明，在受到围岩岩性和应力方向等因素的影响下，井下巷道围岩蝶形塑性区蝶叶形态并不会和图1所示的蝶叶形态严格一致，而是会发生一定程度地改变，如图2所示。

图2 巷道围岩塑性区形态变化示意Fig.2 Schematic diagram of plastic zone morphology change of roadway surrounding rock

根据蝶形破坏理论，导致此类现象出现的原因不仅是由于反映应力场大小的非均匀系数η对蝶形塑性区蝶叶分布范围及尺寸产生影响，应力场方向也会对蝶形塑性区蝶叶位置产生重要影响。

2 蝶叶方向性形成机制

2.1 理论分析

于学馥[21]和马念杰[26-27]等给出了非等压条件下圆形巷道围岩塑性区边界隐性方程为

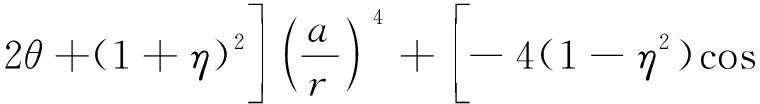
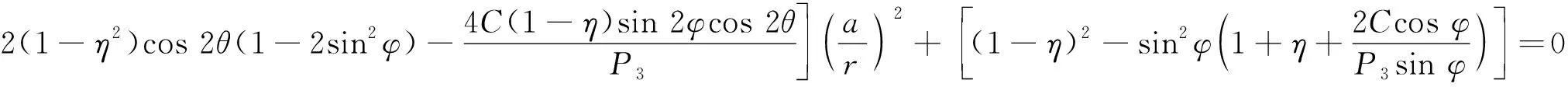
(1)

为分析非静水压力场条件下围岩塑性区蝶叶方向性，在式(1)中引入围岩塑性区主应力方向偏转角度α并进行因式分解可得

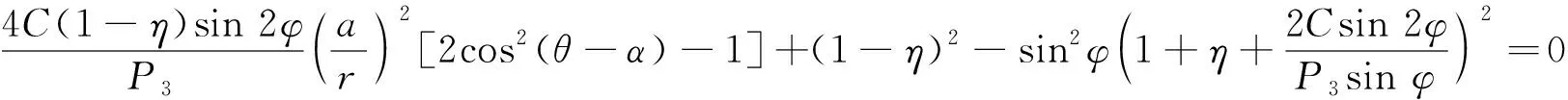
(2)

cos22(θ-α)+sin22(θ-α)=1

(3)

将式(3)代入式(2)并提出公因式，变形可得

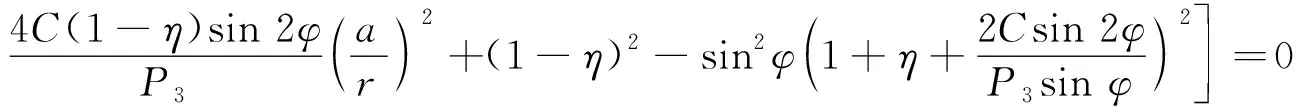
(4)

令:

则式(4)可化简为围岩塑性区主应力方向偏转角度α与极坐标位置角度θ的余弦四次隐性方程:

K1cos4(θ-α)+K2cos2(θ-α)+K3=0

(5)

式中，r为塑性区边界上任一点的半径;C为黏聚力;φ为内摩擦角;η为围压非均匀系数(定义其为最大主应力与最小主应力的比值);θ为塑性区边界上任一点的极坐标角度;α为主应力方向偏转角度(定义其为P3与竖直方向的夹角，顺时针为正)。

分析式(5)隐形方程可知，Ki是关于巷道半径、围岩性质参数、围压以及塑性区半径的函数，而当围岩性质及围压大小一定时，巷道围岩塑性区半径也会为定值，则Ki可以看作常数。此时，塑性区边界上对应点的极坐标角度与主应力方向偏转角度存在如隐形方程所示的函数关系，2者之间的变化会同步发生。当塑性区边界上每一点的极坐标角度因主应力方向偏转而发生改变时，则围岩塑性区整体会发生偏转。

对于井下巷道而言，其原岩应力场中，最大主应力主要以水平应力为主，而采矿活动加载效应引起的采动支承压力集中系数会达到2～3倍，导致巷道围岩所处的应力场中最大主应力不再以水平应力为主。根据式(5)，通过改变主应力方向的偏转角度α，固定其他计算参数不变，得到不同主应力方向下的塑性区边界分布图，并将其与初始主应力方向(最小主应力为竖直方向，最大主应力为水平方向)的塑性区边界分布图进行对比，如图3所示。

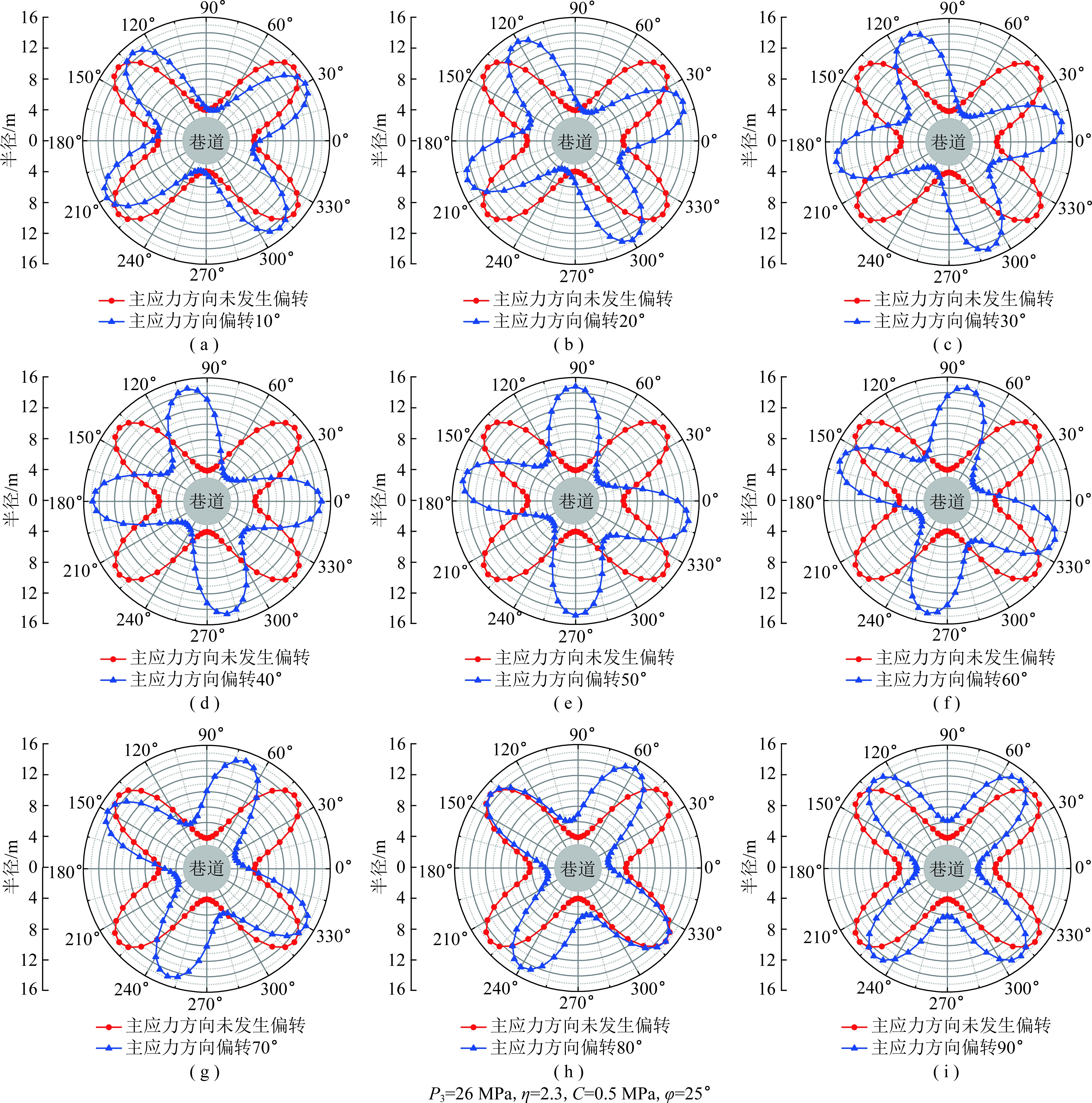
图3 圆形巷道围岩塑性区边界分布对比(理论计算)Fig.3 Comparison of the distribution of the plastic zone boundary of circular roadway rock surrounded (Theoretical calculation)

通过图3可以看出，在非静水压力场环境下，均质圆形巷道围岩会形成蝶形塑性区，且蝶形塑性区的4个蝶叶会随着主应力方向的偏转而随之发生偏转。当主应力方向未发生偏转时，将第1,2,3,4象限的蝶叶分别标记为A，B，C，D，表1为主应力方向偏转不同角度时塑性区4个蝶叶位置的极坐标。由表1可知，围岩塑性区的4个蝶叶位置会随着主应力方向的偏转而改变，且蝶叶位置的偏转角度与主应力方向的偏转角度相等，如图4所示。

图4 主应力偏转角度与蝶叶偏转角度关系Fig.4 Diagram of relationship between deflection angle of principal stress and deflection angle of butterfly leaf

表1 主应力偏转不同角度时塑性区蝶叶位置(理论计算)Table 1 Butterfly leaf position of plastic zone when principal stress deflects different angles(Theoretical calculation)

2.2 数值模拟验证

为了验证理论计算解的可靠性和普适性，利用FLAC3D数值模拟验证圆形巷道围岩塑性区蝶叶的方向性。数值模拟围岩本构模型采用摩尔—库伦模型，模型边界采用应力约束，施加最大主应力60 MPa，最小主应力为26 MPa;当主应力方向发生偏转时，根据弹塑性力学中的应力转换公式进行主应力换算。数值模型巷道半径a=3 m;其余数值模拟参数见表2。

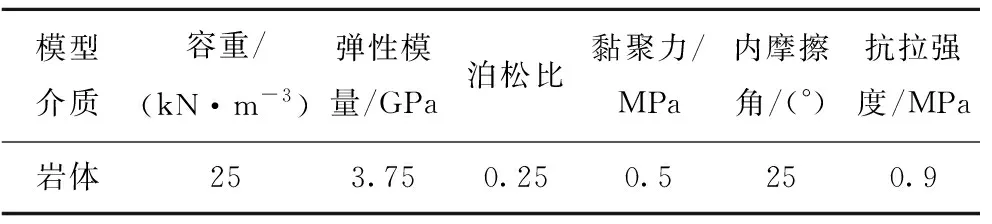
表2 模型力学参数Table 2 Mechanical parameters of model

数值模拟得到的圆形巷道围岩塑性区分布形态如图5所示，以左上角的蝶叶为研究代表，随着主应力方向发生偏转，其与竖直方向的夹角随之改变，蝶叶的偏转角度与主应力方向的偏转角度近似相等(2者差值不超过3°)，见表3。

表3 圆形巷道塑性区蝶叶偏转角度(数值模拟)Table 3 Butterfly leaf deflection angle in plastic zone of circular roadway(Numerical simulation)

图5 圆形巷道围岩塑性区分布形态示意(数值模拟)Fig.5 Distribution pattern of plastic zone in circular roadway rock surrounded(Numerical simulation)

综合理论分析和数值模拟可以看出，在相同参数条件下，理论分析和数值模拟得到的结果基本一致。当主应力方向发生偏转时，围岩蝶形塑性区的蝶叶会随之发生偏转，且偏转的角度与主应力方向的偏转角度基本相同，蝶形塑性区蝶叶具有显著的方向性。

3 蝶叶方向性的适用性分析

3.1 巷道断面形状对蝶叶方向性的影响

目前，煤矿井下常见的巷道断面形状有圆形、矩形和拱形。因此，本节将分别通过理论计算和数值模拟的方法研究断面形状对蝶形塑性区蝶叶方向性的影响。受制于现有数学力学方法的限制，矩形巷道和拱形巷道围岩的塑性区无法通过理论计算得到精确解。因此，对拱形巷道与矩形巷道塑性区边界进行理论计算时，采取外接圆的方式并利用式(5)计算得到其主应力方向发生偏转前后的塑性区形态对比图，如图6，7所示，并利用数值模拟进行验证分析。矩形巷道尺寸为4 m×3 m;拱形巷道尺寸为上部半径3 m，下部尺寸6 m×3 m。由图6，7可以看出，随着主应力方向的偏转，拱形巷道与矩形巷道的蝶形塑性区蝶叶同样会随之发生偏转，且两者的偏转角度相等(表4)。

图6 拱形断面巷道塑性区理论计算结果Fig.6 Theoretical calculation result of plastic zone in arched roadway

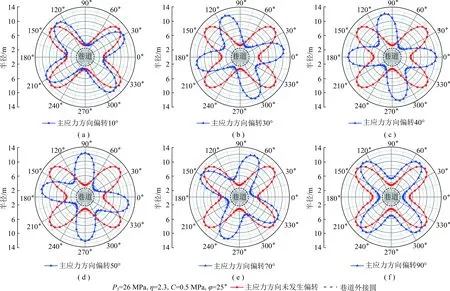
图7 矩形断面巷道塑性区理论计算结果Fig.7 Theoretical calculation result of plastic zone in rectangular roadway

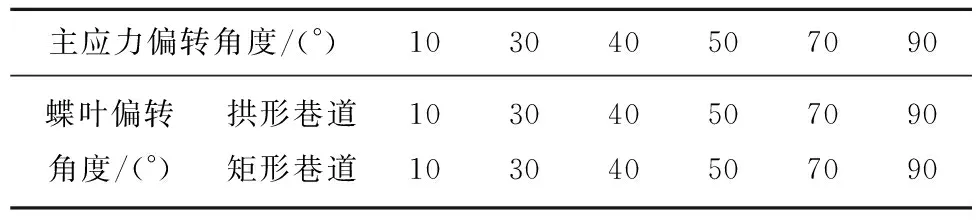
表4 不同巷道断面形状塑性区蝶叶偏转角度(理论计算)Table 4 Deflection angle of butterfly leaf in plastic zone of different roadway shapes (Theoretical calculation)

为了验证上述理论计算的可靠性，采用数值模拟对矩形和拱形巷道的塑性区分布进行验证分析，数值模拟参数与理论计算保持一致，见表5，其他模拟初始条件参数与圆形巷道相同。

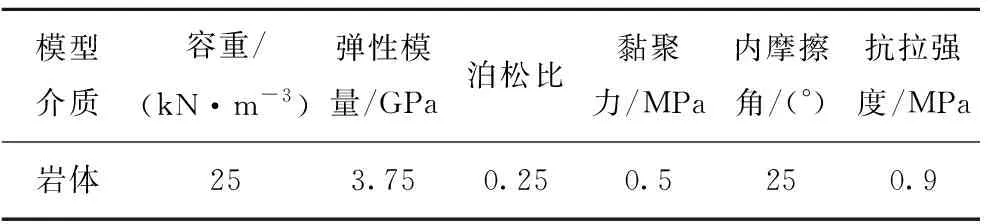
表5 数值模拟力学参数Table 5 Numerical simulation of mechanical parameters

数值模拟得到的不同巷道断面形状的塑性区分布形态如图8所示，并以左上角的蝶叶为例，得到了蝶叶随主应力方向发生偏转时，其与竖直方向的夹角。由图8可以看出，当主应力方向发生偏转时，不同巷道断面形状条件下的围岩塑性区蝶叶位置均会发生偏转，且蝶叶位置的偏转角度与主应力方向的偏转角度基本一致，误差不超过3°，见表6。因此，围岩蝶形塑性区蝶叶的方向性与巷道断面形状无关。

图8 不同巷道断面形状塑性区分布形态Fig.8 Distribution pattern of plastic zone in different shape of roadway

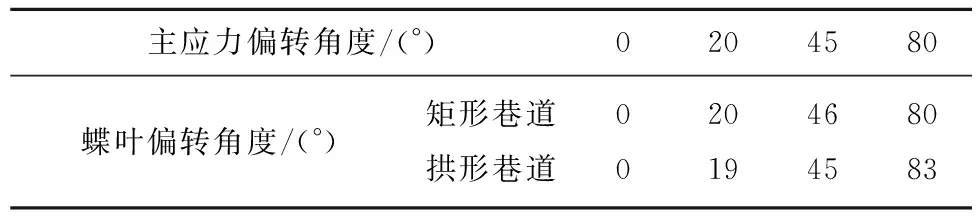
表6 不同巷道断面形状塑性区蝶叶偏转角度(数值模拟)Table 6 Deflection angle of butterfly leaf in plastic zone of different roadway shapes(Numerical simulation)

3.2 围岩性质对蝶叶方向性的影响

由于煤系地层多为沉积形成的层状岩体[28]，井下巷道围岩基本为沉积岩，造成不同岩层之间的围岩力学性质差异明显。因此，为了研究围岩性质对蝶形塑性区蝶叶方向性的影响，本节先对不同力学参数条件下围岩蝶形塑性区蝶叶方向性进行研究，再通过数值模拟研究巷道复合顶板条件对蝶形塑性区蝶叶方向性的影响。

3.2.1力学参数

通过理论计算得到不同力学参数条件下圆形巷道围岩蝶形塑性区分布图，如图9所示。由图9可以看出，不同力学参数条件下，蝶形塑性区蝶叶均会随着主应力方向的偏转发生偏转，且偏转角度与主应力方向偏转角度一致，见表7。因此，蝶形塑性区蝶叶的方向性与围岩力学参数条件无关。

表7 不同力学参数下塑性区蝶叶偏转角度(理论计算)Table 7 Deflection angle of butterfly leaf in plastic zone under different mechanical parameters (Theoretical calculation)

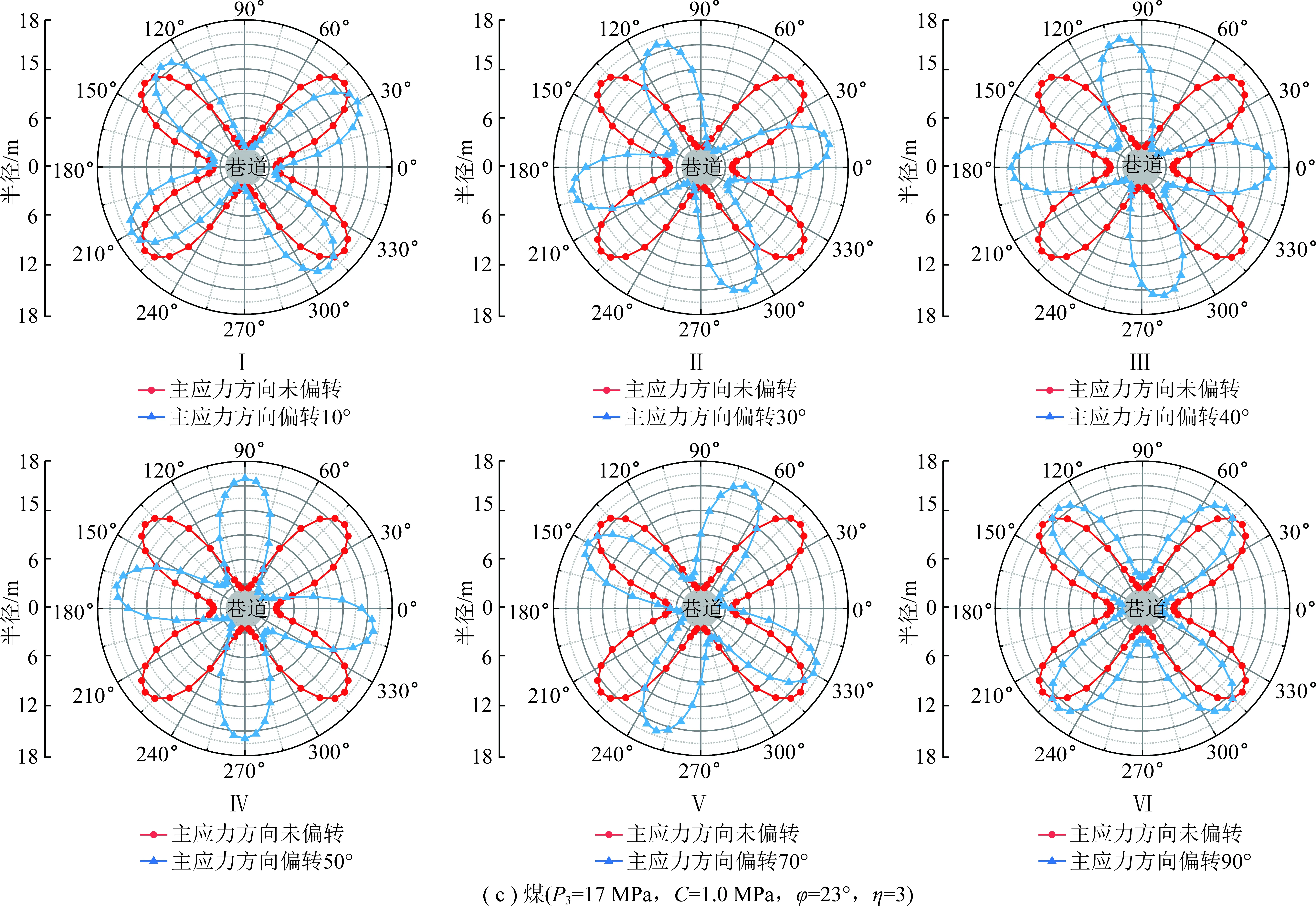
图9 不同力学参数下塑性区边界理论计算分布Fig.9 Theoretical calculation distribution of plastic zone boundary under different mechanical parameters

同时，通过数值模拟得到了不同围岩力学参数条件下巷道围岩塑性区分布图，并以左上角的蝶叶为代表，得到其与竖直方向的夹角，如图10所示。可以看出，不同围岩力学参数条件下的围岩塑性区的形态均呈蝶形形态，虽然蝶叶的形状会因围岩力学参数的不同存在差异，但当主应力方向发生偏转时，围岩塑性区都会随之偏转，蝶叶位置也会随之发生改变，且偏转角度都与主应力方向偏转角度基本相同，误差不超过3°，见表8。

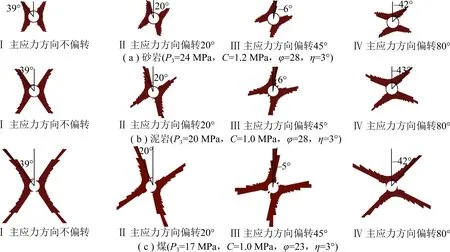
图10 不同力学参数下塑性区分布形态数值模拟Fig.10 Numerical simulation of plastic zone distribution under different mechanical parameters

表8 不同力学参数下塑性区蝶叶偏转角度(数值模拟)Table 8 Deflection angle of butterfly leaf in plastic zone of different mechanical parameters (Numerical simulation)

3.2.2层状岩层

由于层状岩层条件下的塑性区无法利用理论计算得到，故利用数值模拟对4种类型的层状岩层顶板结构的围岩塑性区分布形态进行研究，分别为下软上硬型、下硬上软型、软弱夹层型及坚硬夹层型顶板结构，各结构组成见表9，岩层及其岩石力学参数见表10，模拟结果如图11所示。

表9 层状结构顶板岩性组成Table 9 Lithologic composition of layered roof

表10 模型岩层力学参数Table 10 Mechanical parameters of model rock stratum

图11 层状岩层顶板条件巷道围岩塑性区形态Fig.11 Plastic zone of surrounding rock of roadway under condition of layered rock roof

由图11可知，由于顶板层状岩层的围岩性质存在差异，因此围岩中较为坚硬岩层的存在会限制蝶叶塑性区的扩展，甚至使塑性区出现彻底隔断[29]，同时，受到围岩岩性的影响，塑性区蝶叶会发生不同程度的退化等变异现象[25]。但蝶叶方向性不会因发生变异或塑性区隔断现象而消失，塑性区蝶叶同样会随着主应力方向的偏转而偏转，且两者偏转角度基本保持一致，误差同样不超过3°，见表11。

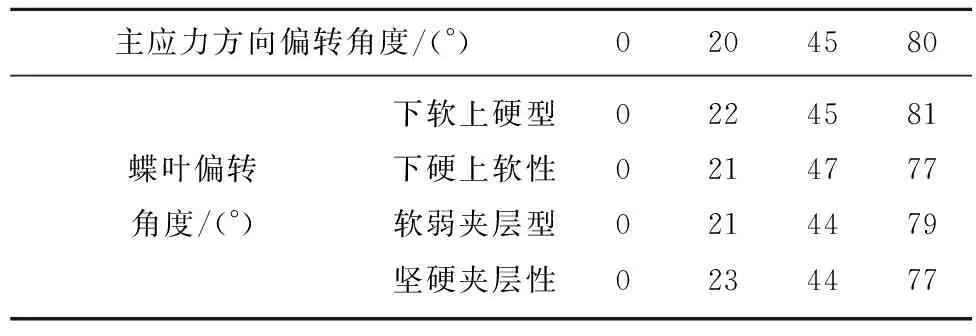
表11 层状岩层顶板条件巷道围岩塑性区蝶叶偏转角度 (数值模拟)Table 11 Butterfly leaf deflection angle in plastic zone of roadway surrounding rock under roof condition of layered strata (numerical simulation)

综上所述，不同巷道断面形状和围岩性质条件下，蝶形塑性区蝶叶均会随主应力方向偏转而发生偏转，且两者的偏转角度基本相等(误差不超过3°)，蝶形塑性区蝶叶方向性与断面形状和围岩性质无关，具有普适性。

4 蝶叶方向性对围岩稳定性的影响

为了分析巷道围岩变形量与围岩蝶形塑性区形态的联系，利用FLAC3D数值模拟得到了围岩主应力方向偏转40°时(图12)的围岩塑性区分布形态及巷道变形量等值线云图。

由图12可以看出，巷道顶板左侧上方岩层、巷道左帮上部围岩、巷道右帮下部围岩和顶板右侧下部围岩由于形成了蝶叶塑性区，其塑性区尺寸较大，且与之对应的左侧上方岩层的下沉量、巷道左帮上部围岩和巷道右帮下部围岩的变形量、顶板右侧下部岩层的底臌量也比巷道其他位置围岩变形量大，巷道围岩变形量和塑性区尺寸呈正相关性。

图12 主应力方向偏转40°时塑性区与位移关系对比Fig.12 Comparison of the relationship between plastic zone and displacement when the principal stress direction is deflected by 40°

同时，通过对比分析不同主应力方向下矩形巷道蝶形塑性区分布图(图8(a))可以看出，主应力方向未发生偏转时，巷道塑性区蝶叶主要位于巷道4个尖角处的深部围岩中，这与普遍认为矩形巷道尖角处围岩的变形破坏较严重是相符的;而当主应力发生偏转时，巷道塑性区蝶叶不再位于巷道尖角处位置围岩中，其会随着主应力方向偏转而位于巷道不同位置的围岩中，这就解释了在某些深部巷道中其变形破坏严重的位置并非一定出现在巷道尖角处，蝶叶方向性会导致围岩的变形破坏具有非对称性。

综上所述，蝶形塑性区的蝶叶即为围岩塑性破坏范围，而蝶形塑性区尺寸与围岩变形量呈正相关性。当围岩塑性区的形态不再呈现均匀形态而呈现为蝶形分布形态时，蝶形塑性区蝶叶方向性会使蝶叶位于巷道围岩的不同位置，导致巷道围岩不同位置的变形破坏呈现差异化分布特征。尤其当塑性区蝶叶位于巷道顶板位置时，蝶叶塑性破坏范围会成为巷道顶板的冒顶高风险区域。在实际工程中，由受围岩低抗拉特性及节理化等特征的影响，巷道的实际冒顶形态与顶板塑性区蝶叶形态无法完全吻合，但产生蝶叶塑性区的顶板位置仍是冒顶的高发区域。

5 工程应用

赵固二矿11030工作面运输巷与11011采空区留设8 m窄煤柱掘进(图13)，断面尺寸高3.3 m×宽4.8 m，埋深700 m左右，巷道顶板岩层主要为泥岩、砂质泥岩和大占砂岩，底板岩层为砂质泥岩和泥岩。该巷道掘进期间，巷道断面收敛严重，矿压显现剧烈。现场矿压监测数据显示，巷道围岩变形呈现明显的非均匀大变形特征，如图14所示。

图13 巷道位置与工作面布置Fig.13 Roadway location and working face layout

图14 11030运输巷非均匀变形特征Fig.14 Non-uniform deformation characteristics of 11030 headgate

11303运输巷围岩破坏现场探测如图15所示，根据文献[30]研究，当煤柱尺寸为8 m时，围岩应力场主应力方向大致会逆时针偏转20°左右，导致其围岩塑性区分布特征如图16所示，塑性区蝶叶分别位于巷道顶板煤柱帮侧、底板煤壁帮侧、煤柱帮煤体及煤壁帮煤体，与围岩现场探测破坏形态基本吻合。

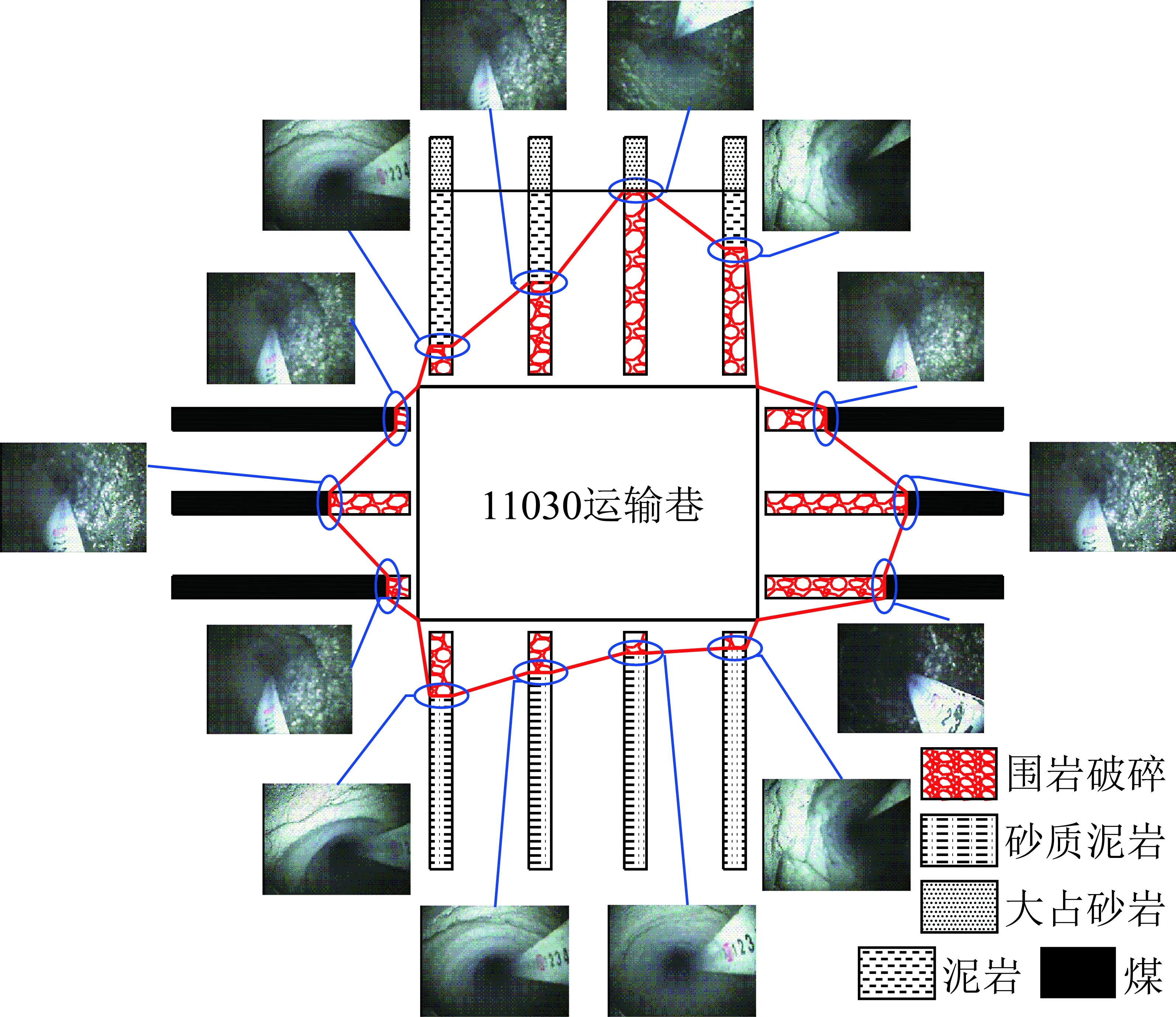
图15 11030运输巷围岩破坏现场探测Fig.15 Field detection diagram of surrounding rock failure of 11030 headgate

通过对比11030运输巷巷道变形特征和11030运输巷由数值模拟得到的围岩塑性区分布形态可以看出(图16)，巷道围岩塑性区分布形态与围岩的非均匀大变形特征高度一致。围岩应力场主应力方向偏转导致塑性区蝶叶分别位于巷道围岩不同位置，塑性区深度较大的蝶叶位置的围岩变形量相对较大。因此，蝶叶方向性是导致巷道围岩出现非均匀大变形的主要原因。

图16 11030工作面运输巷围岩非均匀变形破坏机理Fig.16 Non-uniform deformation failure mechanism diagram of 11030 headgate rock surrounded

6 结 论

(1)当主应力方向发生偏转时，蝶形塑性区蝶叶会随之发生一定的偏转，且主应力方向偏转角度与蝶叶偏转角度基本相等，蝶形塑性区蝶叶具有显著的方向性。

(2)不同断面形状和围岩性质条件下的巷道蝶形塑性区蝶叶，均会随主应力方向偏转而随之发生偏转，即蝶叶方向性不受断面形状及围岩性质的影响，具有普适性。

(3)蝶形塑性区蝶叶方向性决定了蝶叶产生的位置，导致蝶叶位置的围岩变形破坏程度相对严重，且巷道围岩的变形破坏特征与蝶形塑性区分布特征高度一致。