混合级联型多电平逆变器共模电压优化方法

余亚东，李杰 ，王乐，薛亚许

（1.平顶山学院电气与机械工程学院，河南 平顶山 467000；2.深圳市禾望电气股份有限公司，广东 深圳 518055）

目前混合级联型多电平逆变器结构以全桥拓扑为主要结构，因其输出谐波小、易于控制等优点获得了工业界的青睐。但是全桥拓扑结构在以电机作为负载时，频率越高，在负载端产生的共模电压就越高，这一现象势必会造成电动机的过电压，进而加速轴承绕组的老化[1]。同时共模电压通过在PWM调制逆变器调制的电机内部与寄生电容形成回路产生漏电流，这将引起电机保护装置的误动作。同时，当共模电压对电机调速系统中的耦合电容等容性元件进行激励时，这也会引起危害性的共模漏电流，其可通过调速系统中的导电元件流回电网系统中，进而产生电磁干扰EMI，影响大电网上挂接设备的顺利运行。由此可知，共模电压的存在降低了整个系统的可靠性，实际损失不可估量。为了有效减小共模电压对电力设备的影响，对共模电压研究是必要的。

为了改善共模电压对系统带来的不利影响，文献[2]提出了使用无源滤波器的方法来抑制共模电压，该方法可以有效地抑制过电压的幅值，但是系统频率改变时，该方法对逆变器的谐波的限制能力较弱[3]。因此又有学者提出了使用有源滤波器的方法来完全消除共模电压[4−7]。这些方法虽然在抑制共模电压方面有一定的作用，但硬件成本较高。若采取一些相关的方法在控制算法上进行创新，则可以在不增加硬件的基础上，实现对共模电压的抑制或消除，将是相对比较好的办法。文献[8]将五段式SVPWM调制策略应用于非对称三电平逆变器中，确保了系统具有低的开关损耗及谐波量，这对非对称型多电平逆变器的设计具有重要的参考价值[9]。文献[10]通过对比分析多种PWM控制算法对共模电压的抑制效果，得出了SVPWM算法对共模电压的抑制是众多算法中的佼佼者。以上只是在抑制共模电压方面起到了一定作用，为了完全消除共模电压，文献[11]将载波算法应用于NPC变流器中，在消除共模电压方面具有明显优势，但是对逆变器的输出电压THD的限制较弱。为了既能完全消除共模电压又能有效限制输出电压THD值，文献[12−13]均提出了一种以基本矢量为单元重新合成参考矢量的方法，但这些算法只适用于电平数目很高的情况。

上述学者的研究大多是针对标准型逆变器输出共模电压控制算法的研究，少有学者针对混合级联型多电平逆变器的共模电压进行研究，本文基于旋转坐标变换，以混合级联型二级七电平逆变器输出的共模电压基本矢量在坐标平面中的分布特点作为切入点，提出了一种广泛适用于混合级联型的二级七电平逆变器共模电压消除的优化控制算法，搭建了相关的实验平台，实验结果验证了本文提出的优化控制算法的正确性，同时可为混合级联型的多电平逆变器共模电压的消除提供重要的技术支撑。

1 混合级联型逆变器共模电压矢量分布特点

本文将采用经过45°旋转后的α′−β′坐标平面为研究基础，假设Uα，Uβ和Uα'，Uβ'分别为α −β坐标系中的坐标值和α′−β′坐标系中的坐标值，根据两者的关系可得关系式如下：

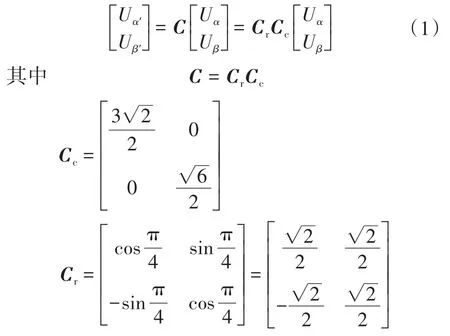
式中：Cr为轴向压缩矩阵；Cc为45°顺时针旋转变换矩阵。

为了满足矢量的精准定位需要，可将α′−β′坐标系中的坐标值进行进一步的转化，令旋转坐标系中的三相电压存在的共模电压是α−β坐标系中的共模电压的3倍，这样能够确保旋转坐标系下的基本矢量是整数：

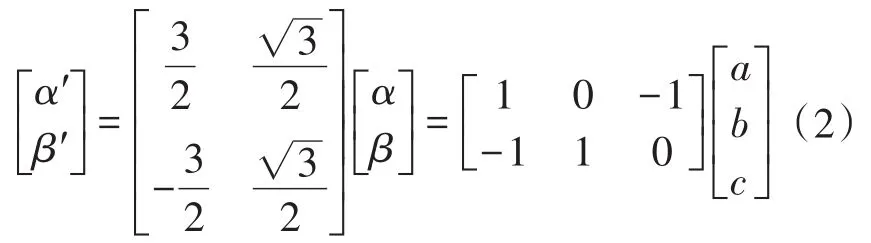
式中：[α′,β′]T，[α,β]T分别为α′− β′坐标系与α−β坐标系下的对应点坐标；[a，b，c]T分别为经过归一变换后的坐标（三相坐标）。

由式（1）、式（2）式可得：a，b，c与α′，β′以及共模电压N的关系式为

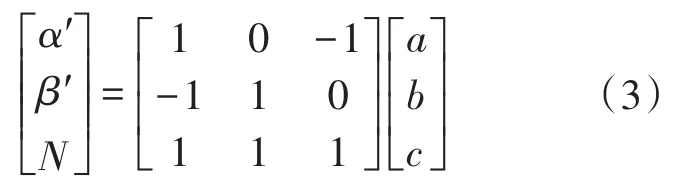
根据式（3）能够得出α′−β′坐标与a−b−c坐标的关系式如下式：

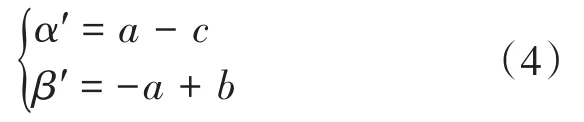
通过求取式（3）的逆矩阵，可得指定共模电压N的基本矢量值U(α′,β′)：

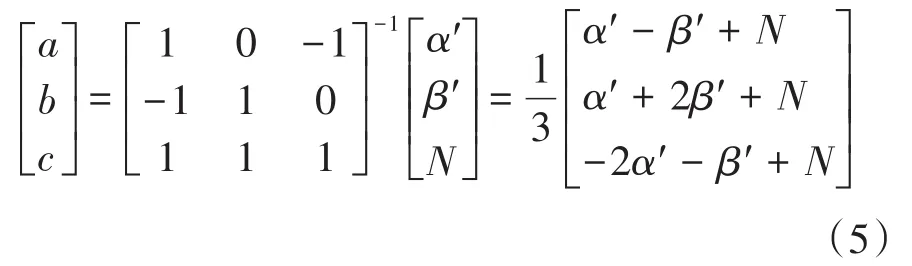
经进一步化简，可得到下式：

则进一步进行转化可得下式：

式中：k为任意整数。

若式（8）成立，那么b，c均为整数也成立。

式（8）表明，在α′− β′坐标系中，所有共模电压的基本矢量是以斜坡函数的方式分布的直线簇，该斜坡函数的斜率为45°，轴截距为L=−3k+N。

令N值分别取−1，0，1代入式（8），可得出下式：

式（9）代表了3簇不同的直线集合。

将式（9）中的α′− β′坐标系中的坐标关系式通过图1进行直观的表示（k分别取值1，0，−1）。

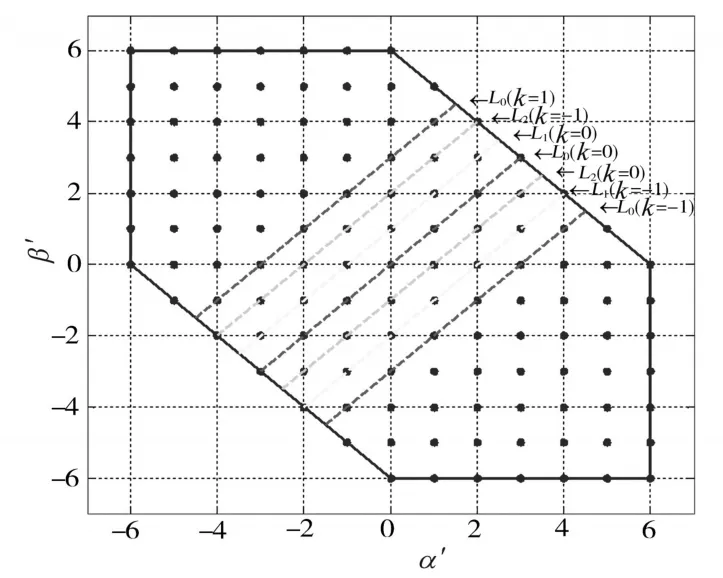
图1 α′−β′坐标平面直线簇图Fig.1 Straight line cluster diagram ofα′− β′coordinate plane

图1中L0，L1，L2直线分别是式（9）中的L0，L1，L2直线簇在共模电压N=0，−1，1时的在α′β′平面中所有共模电压基本矢量点。

为了进一步说明混合型级联逆变器的基本矢量分布规律，本文采用二级七电平逆变器作为研究对象，图2为混合型级联二级七电平逆变器共模电压基本矢量分布图，其中，大圆点为存在的高电压−低频率基本矢量，“+”为同时存在共模电压幅值为1的基本矢量点，存在的其他的标识均为低电压−高频率矢量点。图2中的每一个高电压−低频率基本矢量点均被6个低电压−高频率基本矢量点围绕（空间矢量是立体空间，在每个*的对立面还有3个，由于图2是二维的，无法显示立体空间，所以在图2中无法看到对立面的3个）。

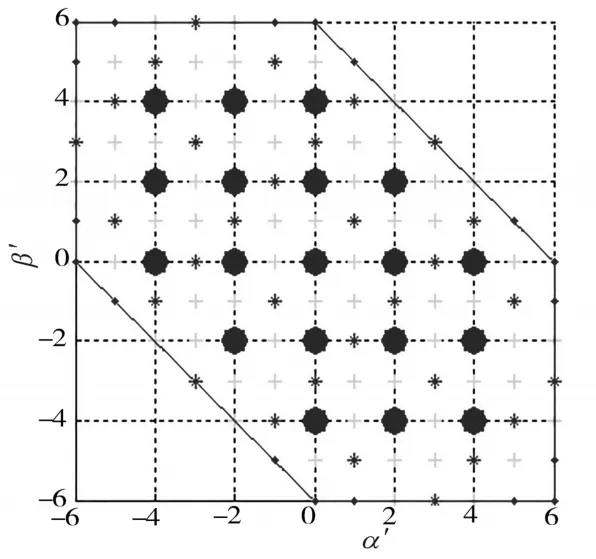
图2 二级七电平共模电压基本矢量分布图Fig.2 The common mode voltage（CMV）vectors distribution for two-stage seven-level

2 参考矢量的定位、合成

2.1 定位特征多边形

在文献[14−15]中以学者王翠和F.d.Morais为代表均提出了在α′−β′坐标系中针对多电平逆变器的快速SVPWM算法，他们对参考矢量的定位办法均是由参考矢量进行数学运算获取在该参考矢量附近的4个基本矢量点。为了使得定位思想更加清晰，笔者进一步将定位思想进行转化处理，参考矢量定位图如图3所示。图3中Vref=（α′r，β′r），通过向上取整和向下取整来获得离参考矢量最近的4个基本矢量V1，V2，V3和 V4。

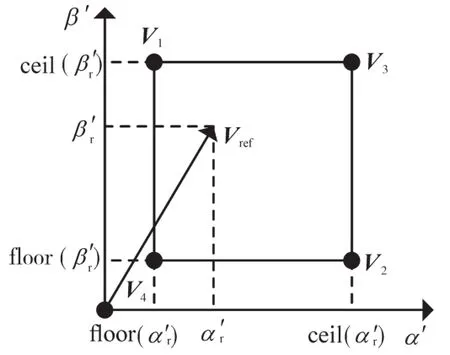
图3 参考矢量定位图Fig.3 Locus of reference vector

通过分析二级七电平基本矢量的分布规律可进行如下规定：由参考矢量进行定位的4个基本矢量点均存在一个高电压−低频率点，故笔者认为用图4将二级七电平共模电压的基本矢量进行限定更加合理。图4中限定的范围为黑色六边形，在该六边形内的矢量为有效矢量。

图4 二级七电平基本矢量限定图Fig.4 The distribution rang of basic vector for 2-stage 7-level

为了进一步在逆变器的输出获取良好的输出波形，笔者又细化了参考矢量的合成和定位，将图3的参考矢量定位分为图5所示的四种典型性代表和图6所示的两种特殊三角形定位图。

儿童画生动、活泼、稚拙、夸张，充满童趣和无限的想象力，有着独特的个性与魅力，不少西方美术大师如克利、米罗、毕加索等曾向儿童画学习，他们常常被儿童画的大胆创新所倾倒。儿童对世界的认知基本上是一张白纸，他们最真最纯的描绘是对美丽的大自然、社会和自己内心世界最真实的情感流露。作为教师，我们更应该在教学上去激发他们的创作兴趣与热情，发掘孩子的想象力和创造力，促进儿童的个性发展。

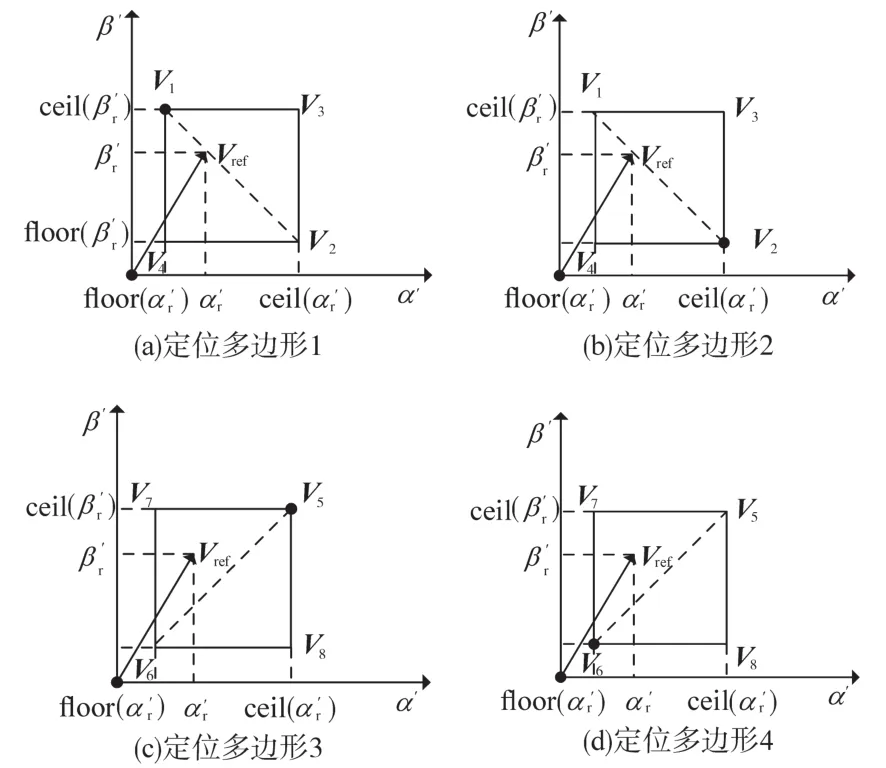
图5 高电压−低频率基本矢量位置图Fig.5 The basic vector position of high−voltage low−frequency

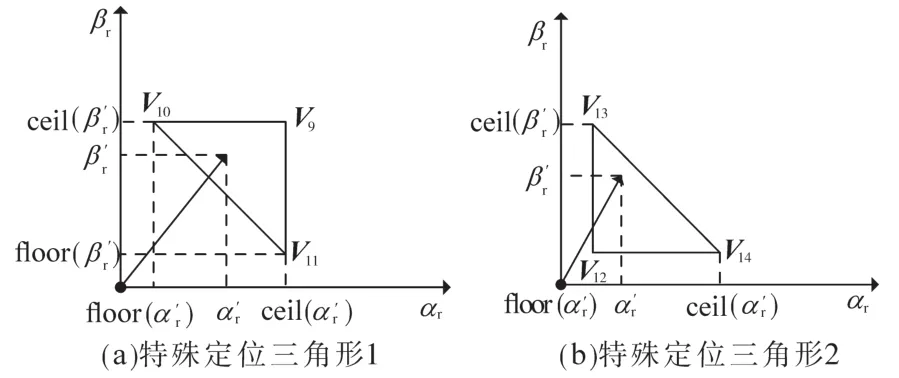
图6 特殊三角形定位图Fig.6 Locus of special triangular

对参考矢量的合成和定位经过细化后，均可从图5中快速地定位到高电压−低频率基本矢量点，可用下式对图5中的4种情况进行合理判断：

式中：下标“r”为参考变量。

上述给出的二级七电平共模电压基本矢量图4中，参考矢量的正方形定位办法对于基本矢量是合理的，但是在基本矢量图中的临近边缘区域存在一些特殊的矢量，该类矢量若采用正方形的定位办法是无法合成和定位的，即合成和定位超出了矢量的分布区域。故为了让合成和定位更加精确，考虑参考矢量存在于基本矢量特殊情况图7所示的左边三角形区域内，需要给出更加精确的定位方程式来表示这些特殊区域的矢量，可用下式来判断参考矢量是否属于这些区域：

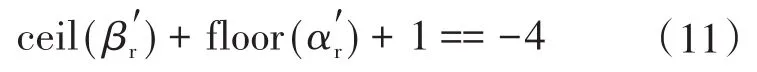
式（11）为参考矢量存在于图7左下区域的判定方程式。同理，根据基本矢量分布对称性，参考矢量存在于图7右上区域的判定方程式：

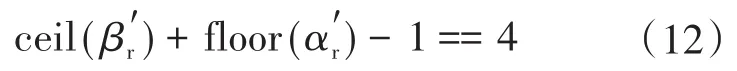
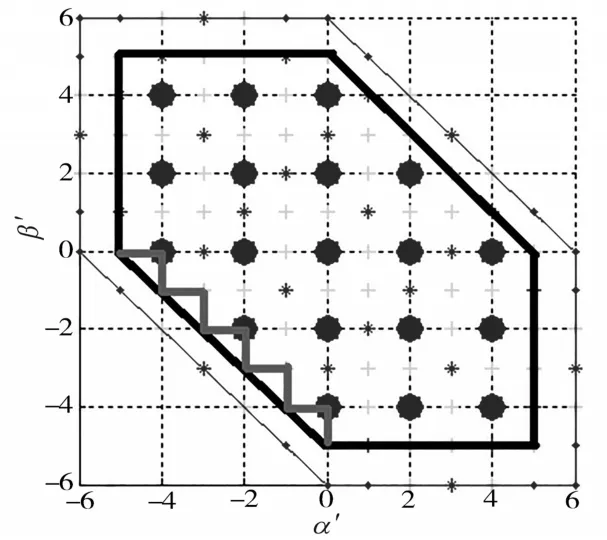
图7 基本矢量特殊情况图Fig.7 Special state schematic of basic vector

2.2 参考矢量的合成

由以上分析可知，式（10）中的4个判定公式对应着图5中的4个定位特征四边形，其中图5中的4个特征四边形可分为两组构成，即图5a与图5b为一组，图5c与图5d为一组。对于基本矢量处于图5a或者图5c的特征四边形内的参考矢量的合成思路为：通过假定在对应的特征四边形内的高低频率基本矢量点为V1和V5，取四边形中的对角线作为另一基本矢量点，根据式（10）来表示V1和V5的坐标值，进而确定对角线的基本矢量点，用V1来表示V2，用V5来表示V6的坐标值。再根据下式来确定基本矢量V3和V4的坐标值：

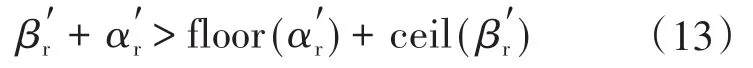
用下式来确定基本矢量V7和V8的坐标值：

对于参考矢量处于图6a或者图6b的特殊左下或右上三角形区域时，其参考矢量的合成思路是根据式（11）和式（12）直接用基本矢量V9，V10，V11和V12，V13，V14来合成参考矢量，其基本矢量的坐标用V1来表示即可。

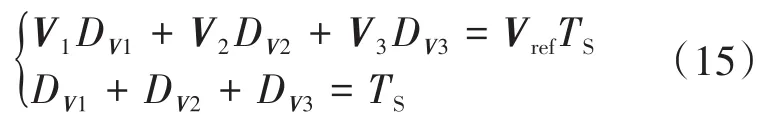
式中：DV1，DV2，DV3分别为3个基本矢量的作用时间；TS为作用周期，一般取1。

求取出基本矢量的作用时间，若不满足式（13）或者式（14），将基本矢量V1，V2，V4或者V5，V6，V8代入伏秒平衡方程式（15）中，求取出基本矢量的作用时间。

对于参考矢量处于图6a或者图6b的特殊左下或者右上三角形区域时的作用时间计算过程是，若参考矢量满足式（11）或者式（12），可将V9，V10，V11或者 V12，V13，V14代入伏秒平衡方程式（15），求取出基本矢量在特殊区域的作用时间。

通过前面针对参考矢量的合成和定位以及作用时间的计算等的合理性分析，本文探究出了一种适合于混合级联型二级七电平逆变器共模电压的优化控制算法，有效地抑制了二级七电平逆变器的共模电压。现将该优化算法表示如下：

1）通过数学模型分析多电平逆变器的输出共模电压，合理分析其基本矢量存在的特点。

2）根据基本矢量存在的特点，用几何图形来确定基本矢量对应的不同情况下的特征多边形。

3）确定参考矢量Vr的坐标（α'r，β'r）存在于图5中的哪个特征区域，针对不同的特征区域采用合适的特征多边形对参考矢量Vr进行重新合成和定位，同时获取参考矢量Vr的3个基本矢量。

4）由步骤3可知参考矢量Vr的3个基本矢量，将其代入相关的伏秒平衡公式，得到3个基本矢量的不同的作用时间。

5）利用混合级联型二级七电平逆变器的输出，验证本算法的正确性。

2.3 基本矢量作用时间计算

对于参考矢量处于图5a或者图5c的特征四边形内的作用时间计算过程是，若参考矢量满足式（13）或者式（14），将基本矢量V1，V2，V3或者V5，V6，V7代入下方伏秒平衡方程式中：

3 仿真与实验分析

为验证本算法的可行性及正确性，本文搭建了混合级联型二级七电平逆变器仿真模型与实验平台。通过本文提出的优化算法，给级联型多电平逆变器的主开关管不同的控制时序，得出本文所需求的电平数，为了分析方便本文在逆变器的输出端连接了一个三相的星型电阻性负载。

3.1 仿真分析

笔者在Matlab中搭建了二级七电平逆变器的仿真模型，仿真模型的一些具体的性能指标如下：调制系数0.877/0.707，采样点数84（每周期点数），采样频率fs=84fr=1.68 kHz，逆变器级数2，运行频率20 Hz。图8为在不同调制比下的二级七电平逆变器输出的相电压仿真波形图。

图8 不同调制比下的相电压仿真波形Fig.8 Simulation waveforms of phase voltage at different modulation ratios

为了更能说明本调制算法的优越性，与文献[16]提出的CMV共模电压消除型算法进行了对比分析，设置调制系数在0.1～0.9范围内变化，获取了不同调制系数下的相电压THD值。图9为在不同调制比下的相电压谐波对比图。

图9 在不同调制比下的相电压谐波对比图Fig.9 Comparison of phase voltage harmonics at different modulation ratios

图10为在不同调制比下的二级七电平逆变器输出的线电压仿真波形图。从图10可以明显地看出混合级联型逆变器的输出线电压波形是较为标准的13电平的调制波形，且波形和正弦波很接近。从波形中可以明显看出文中所设置的调制参数满足基波的基本要求。

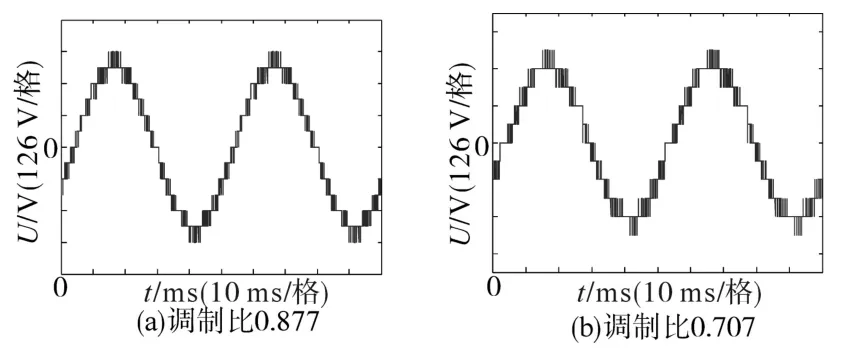
图10 不同调制比下的线电压仿真波形Fig.10 Simulation waveforms of line voltage at different modulation ratios

为了更能说明本调制算法在谐波抑制方面的优势，与文献[16]提出的CMV共模电压消除型算法进行了对比分析，设置两者的调制系数均是从0.1～0.9的变化范围内获取不同调制系数下的线电压THD值，对比图如图11所示。从图11可以明确地看出，本文提出的算法在调制系数大于0.6以后可以将线电压谐波含量控制在10%的附近，谐波含量较少。

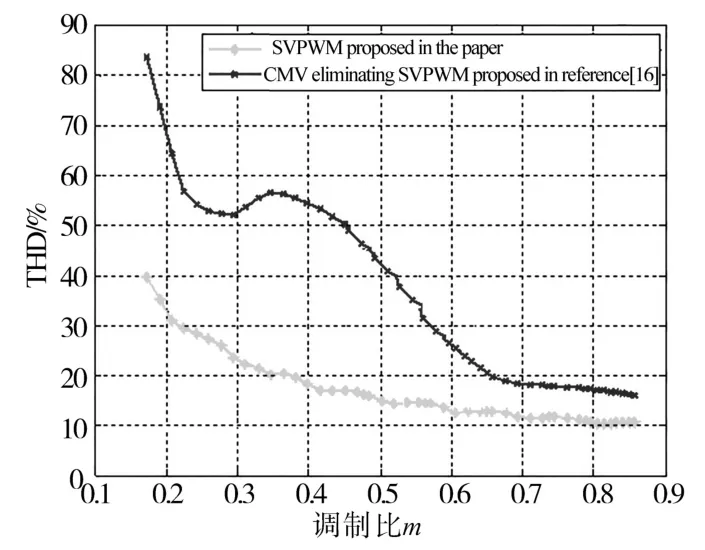
图11 在不同调制比下的线电压谐波对比图Fig.11 Comparison of line voltage harmonics at different modulation ratios

图12给出了与文献[16]提出的CMV共模消除型算法在开关次数的减少方面的对比分析结果图。图12中，两种算法所设置的调制系数均是在0.1～0.9的变化范围内。从图12可以清晰地看出，在调制系数为0.1～0.65的范围内两者在开关次数方面基本相同，但是在0.65～0.9的范围内，本文所提出的算法在开关次数减少方面明显地优于文献[16]所提出的算法。

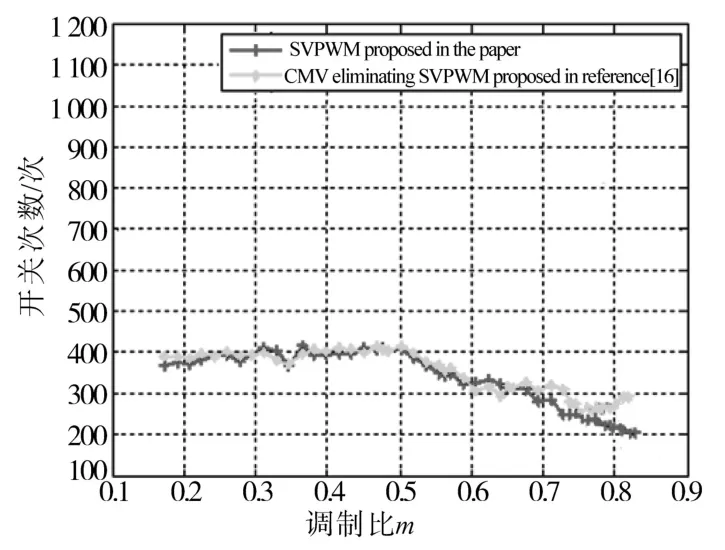
图12 开关次数对比分析图Fig.12 Comparison and analysis diagram of switching times

图13为在不同调制比下的二级七电平逆变器输出的共模电压N仿真波形图。从图13可以明显地看出混合级联型逆变器的输出共模电压的最大幅值一直在−1～1之间，可以将共模电压抑制在1附近，说明抑制效果明显，验证了本算法可以很好地将共模电压的幅值抑制在很小的范围内。

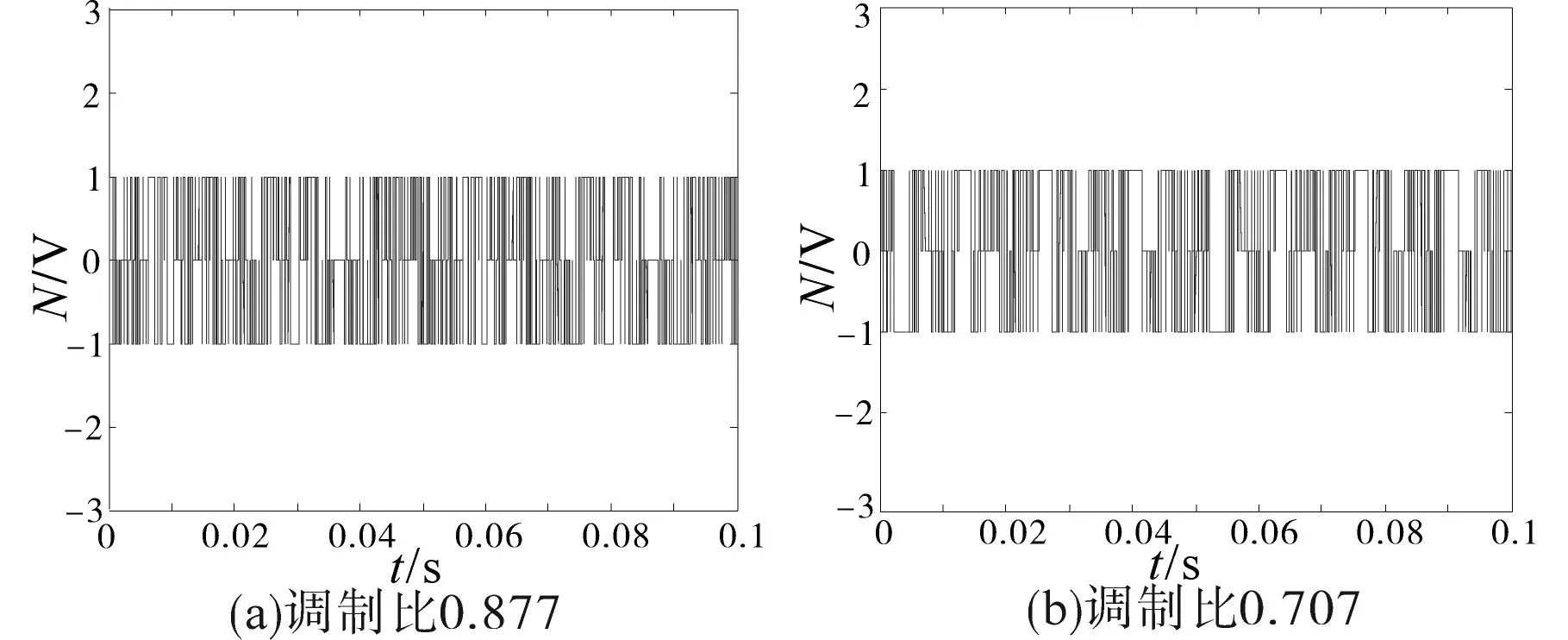
图13 不同调制比下的共模电压仿真波形图Fig.13 Simulation waveforms of common voltage at different modulation ratios

3.2 实验结果分析

为了更能说明问题，笔者在实验室内搭建了实验平台，在该实验平台中所有的性能指标参数均与仿真模型中的参数一致，二级七电平逆变器中的每个单元通过单相桥式整流提供直流电压，作为逆变器的输入，逆变器的开关管选择为能够承受较高电压的IRFP460，控制核心选择为数据处理能力较强的TMS320F28335，使用泰克牌示波器进行波形的测试。

图14为在不同调制比下的逆变器输出相电压实验波形图。从图14可以明显地看出，混合级联型逆变器的输出相电压在不同的调制比下均是较为规整的七电平，与图8中的仿真波形相比，具有较高的吻合度，说明本算法的设计能够满足多电平逆变器的需要。

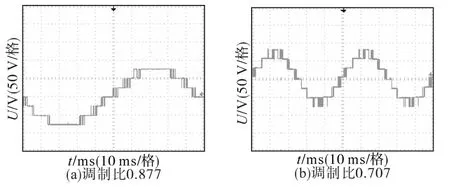
图14 不同调制比下的相电压实验波形图Fig.14 The experimental waveforms of phase voltage at different modulation ratios

图15为在不同调制比下的逆变器输出线电压实验波形图。从图15可以明显地看出混合级联型逆变器的输出线电压的实验波形也是较为标准的13电平调制波形且和正弦波很接近，同时与图10中的仿真波形相比，吻合度也较高。

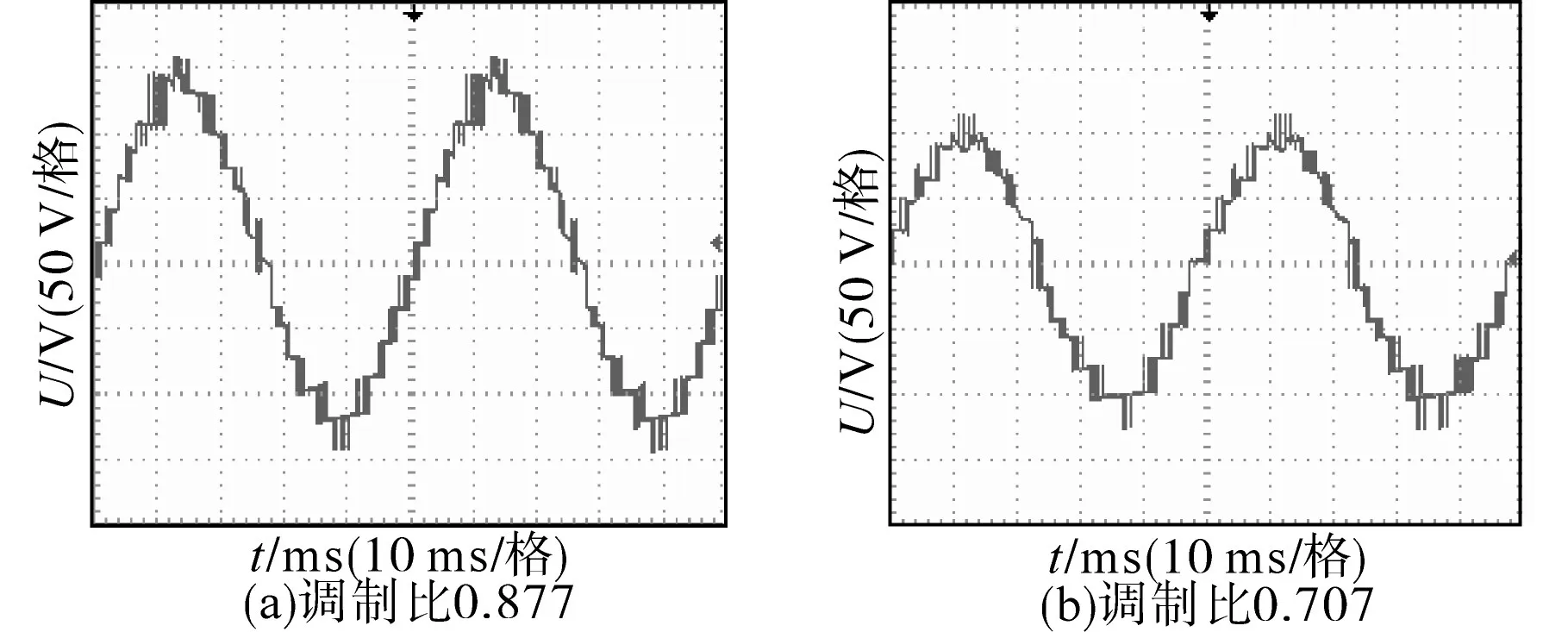
图15 不同调制比下的线电压实验波形图Fig.15 The experimental waveforms of line voltage at different modulation ratios

图16为在不同调制比下的逆变器输出共模电压实验波形图，同时也给出了在该实验平台下未使用调制算法下的共模电压实验波形图。

图16 不同调制比下共模电压和未使用调制算法的实验波形图Fig.16 The experimental waveforms of commom voltage with the algorithm at different modulation ratios and without the algorithm

从图16中可以明显地看出在本文提出的调制算法下混合级联型逆变器的输出共模电压能够较好地抑制在较小的范围内，同时给出了在相同的实验平台下未使用任何的调制算法下混合级联型逆变器输出共模电压实验波形，通过对比分析可以明显地得出本算法对抑制共模电压的能力较强，进一步说明了本算法的正确性。

4 结论

本文首先针对多电平逆变器输出的共模电压的基本矢量在旋转坐标系下的分布规律入手，合理地将其基本矢量限定在不同类型的特征多边形内，依据该类特征多边形使用不同的数学约束模型对参考矢量进行了重新的定位与合成，获得了基本矢量的作用时间；其次给出了本文提出的优化算法的一般性步骤；最后通过搭建二级七电平的逆变器的仿真模型和实验平台，依据二级七电平逆变器输出的相电压、线电压和共模电压以及谐波的波形分析，有力地证明了本优化算法的正确性。