基于多模式控制策略的半桥转换器开关控制方法
张建平,王瑞
(中原科技学院机电工程学院,河南 郑州 450000)
随着计算机工业和电信网络的快速发展,提高电源效率变得越来越重要。在各种通信设备中,系统能耗占很大比例,其功率损耗主要在其电源转换器中。
具有非对称占空比控制的半桥转换器由于其众多优点,成为合适的转换器之一,这些优点包括组件数量少、控制方法简单以及零电压开关(zero volage switching,ZVS)无需任何额外的组件和开关上的钳位电压应力[1−4]。非对称半桥转换器还具有一些缺点,例如:变压器的偏置电流会引起磁化并增加铁心损耗,尤其是在为保持时间要求而设计的转换器中。此外,仅在有限的负载范围内才能实现完整的ZVS,在轻负载条件下,开关损耗会更高,效率会降低。为了解决非对称半桥转换器的缺点,学术界开展了许多研究。文献[5]提出在输出整流器上增加一个隔离电容器,以使变压器的直流偏置电流变为零。但是,这会产生较大的二次循环电流,从而导致较大的传导损耗并降低整体转换效率。文献[6]则通过添加一个有源缓冲电路来修改半桥转换器的次级侧结构,该有源缓冲电路使DC偏置电流减小。但是,未考虑轻载条件的效率。此外,为了在整个负载条件下实现高转换效率,非对称半桥转换器应具有较宽的ZVS范围。在以前研究中,文献[7−8]提出了带有外部谐振电感器的非对称半桥转换器。尽管外部谐振电感器增加了ZVS范围,但整流器的电压应力相应增加。文献[9]提出通过用开关代替低压侧钳位二极管并增加辅助绕组来改变变压器匝数比,以增加ZVS范围和保持时间。但是,增加的元件增加了转换器的成本和复杂性。在文献[10]中,升压转换器级联到非对称半桥转换器,以解决保持时间及其对直流偏置电流的影响的问题。尽管这种结构减少了直流偏移损耗,但它也增加了控制的要素和复杂性。
在本文中,针对上述问题,为了在负载电流的整个范围内提高半桥转换器的效率,提出了一种新颖的开关控制方法。该方法首次提出半桥转换器的多模式控制策略,可以通过低成本的数字控制器来实现,同时避免通过附加组件对基本转换器的结构进行任何修改。所提出的方法使用四种主要的控制模式,包括非对称、相位变化(phase shift,PS)、脉冲宽度调制(pulse width modulation,PWM)和突发控制。尽管这些方法在整个负载条件下都不是最佳方法,但实验结果证明了它们在特定负载子范围内的优越性。因此,本文所提的开关控制方法包括了四类控制模式。为了确定不同控制模式之间过渡点,根据负载电流和转换器参数分别计算每种控制模式的功率损耗,然后根据它们的交点获得过渡点。这些过渡点是负载电流的特定值,将负载电流的整个范围分为四个子范围。数字控制器通过将负载电流与这些转换点进行比较来选择控制模式。本文所提出方法的重要特征之一是通用性,它适用于提高任意给定的基本半桥转换器的效率。
1 功率损耗分析
基本的半桥转换器如图1所示。为了简化分析,考虑了以下假设:
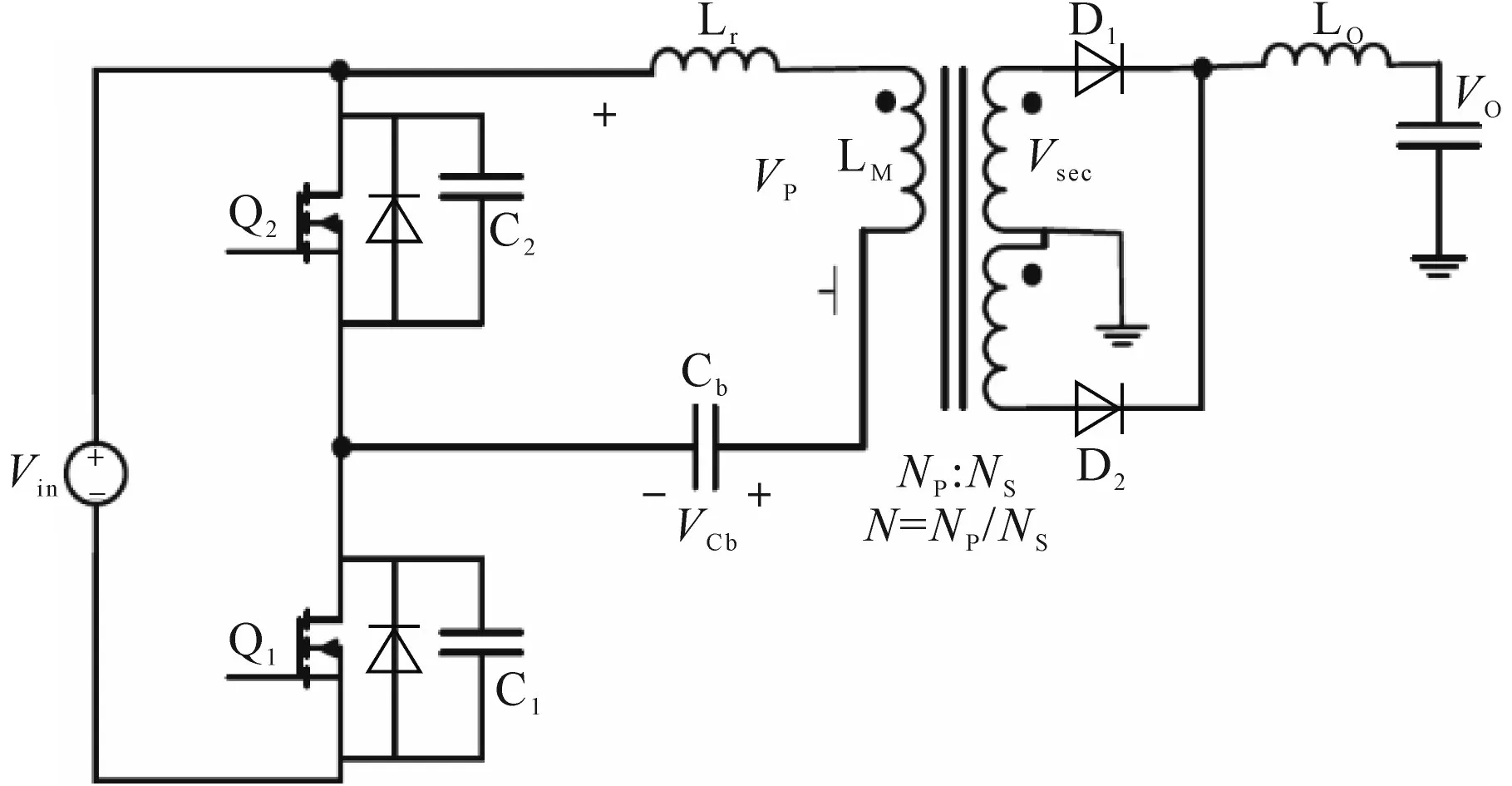
图1 基本半桥变换器Fig.1 Basic half-bridge converter
1)开关损耗、传导损耗和磁损耗视为总功耗;
2)由于与功率损耗相比值较低,因此可以忽略栅极驱动器的损耗;
3)转换器的元素参数由制造商提供。
1.1 非对称控制模式下的功率损耗
非对称控制中的半桥转换器的工作波形如图2所示。
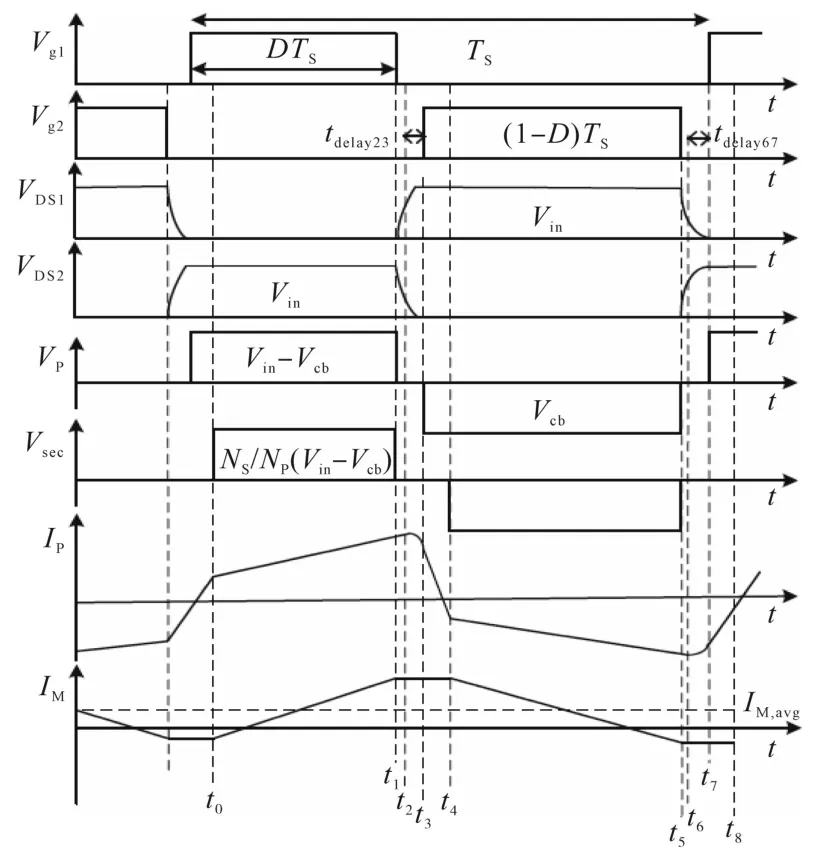
图2 半桥变换器在不对称控制模式下的工作波形Fig.2 Operation waveforms of half-bridge converter in asymmetry control mode
文献[11]中的等效电路描述了非对称控制模式下转换器的工作原理。Ip(tn)为tn处的变压器一次电流,VDS1(tn)和VDS2(tn)为在tn(n=0,1,...)时Q1和Q2的漏源电压。直流增益是输出电压与输入电压之比,VCb为 Cb两端电压,IM,avg为平均磁电流。此外,IQ1,rms,IQ2,rms,ID1,rms,ID2,rms,ILo,rms和 Ip1,rms分别为开关、二极管、输出电感和变压器一次侧的有效值电流。在t0处,Q1接通,并且将Vin~VCb施加到变压器的一次侧。在此时间间隔内,变压器一次电流IP为反映输出电流(IO/N)与变压器磁电流IM的总和。在时间t1,Q1关闭并且IP对电容器C1进行充电,并对电容器C2进行放电,该间隔持续到变压器二次侧电压达到零为止。换句话说,直到在时刻t2将C2电压放电到VCb为止。由于变压器耦合,C2由谐振电感Lr和输出电感LO中存储的能量放电。在时间t2,变压器两端的电压变为零,IO通过输出整流器循环,而C2仅通过Lr中存储的能量继续放电。C2完全放电后,Q2两端的电压达到零,Q2本体二极管在t3开始导通,并且Q2在ZVS条件下导通。因此,将Q2的ZVS条件确定为
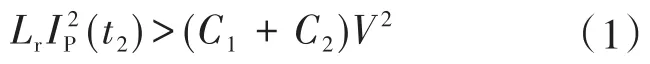
在此时间间隔内,Lr两端的电压为−VCb,IP减小,并且没有能量传输至2次级。此间隔称为占空比(D)损耗。在t4时,IP和IM的总和达到–IO/N。此时间间隔所需的时间通过以下方式获得:
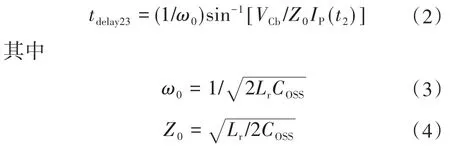
式中:ω0为角谐振频率;Z0为谐振的特性阻抗;COSS为场效应晶体管的寄生电容。
Q2在 t5时关断,IP对 C2充电,同时对 C1放电。此模式一直持续到变压器一次侧电压,VP在时间t6变为零(直到C1放电到Vin−VCb)为止。由于二次侧、一次侧连接,C1使用存储在Lr和LO中的能量放电。在t6时,VP变为零,同时二次侧解耦。因此,IO通过二次侧循环,并且C1继续使用Lr中存储的能量进行放电。C1在t7完全放电后,Q1的本体二极管开始导通,并且Q1达到ZVS。Q1的ZVS条件确定为
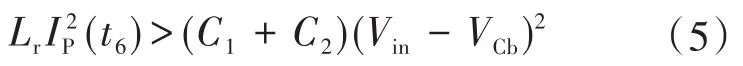
在此模式下,Vin−VCb跨越Llk,并且IP增加。此模式一直持续,直到IP–IM达到IO/N。此间隔所需的延迟时间表示为
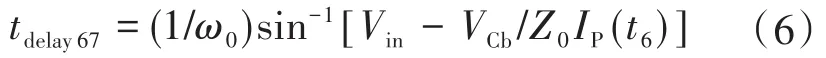
由于IP(t2)总是大于IP(t6),VCb总是小于Vin−VCb,所以式(1)的ZVS条件比式(5)容易得到。
场效应晶体管开关的开关损耗按下式计算:
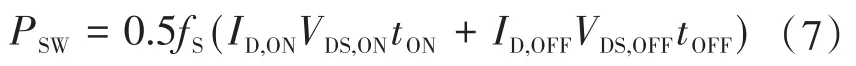
式中:VDS,ON,ID,ON,VDS,OFF和ID,OFF分别为场效应晶体管在通电(tON)和关断(tOFF)时间的漏源电压和电流;fS为开关频率。
Q1和Q2的开关损耗可以用式(7)中开关接通和断开时的电压和电流代入,并用下式表示:
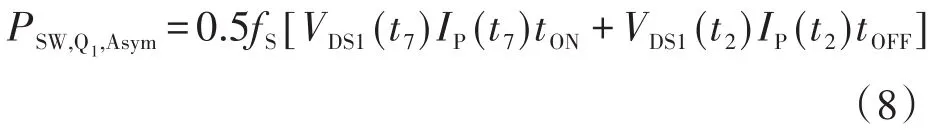
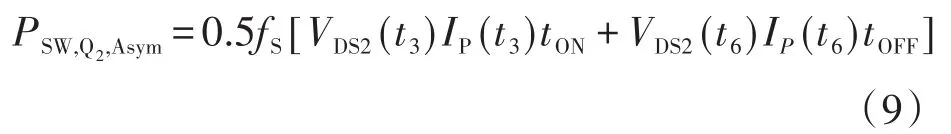
此外,二极管的开关损耗计算如下:
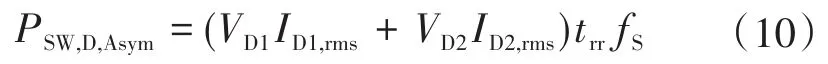
式中:trr为二极管的反向恢复时间。
磁性元件单位体积的磁芯损耗由广义Stein⁃metz方程[12]计算,其表示为
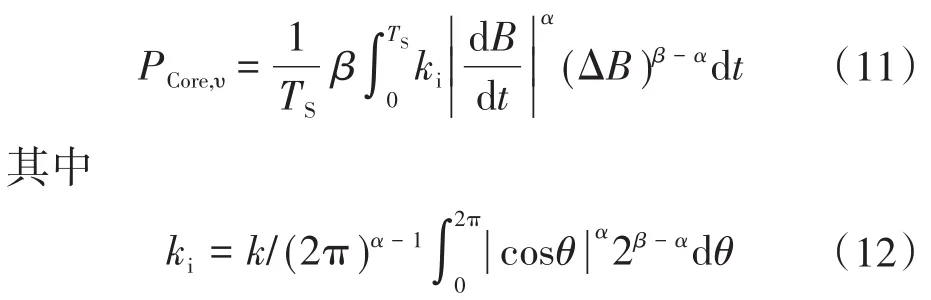
式中:TS为开断周期;ΔB为峰值磁通密度;α,β和k为Steinmetz参数。
如前所述,在这种控制模式中存在一个直流偏移电流,它提供直流磁场HDC(预磁化),同时增加磁损耗。HDC计算如下:
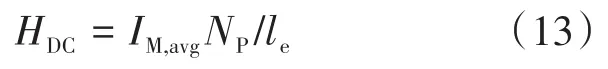
式中:le为有效的磁垫长度。
由文献[12]可知,HDC影响ki和β参数值。换句话说,这些参数取决于HDC(β=f(HDC)和ki=f(HDC)),由图3的Steinmetz参数图确定,并且β0和ki0为零预磁化(HDC=0)时的Steinmetz参数。
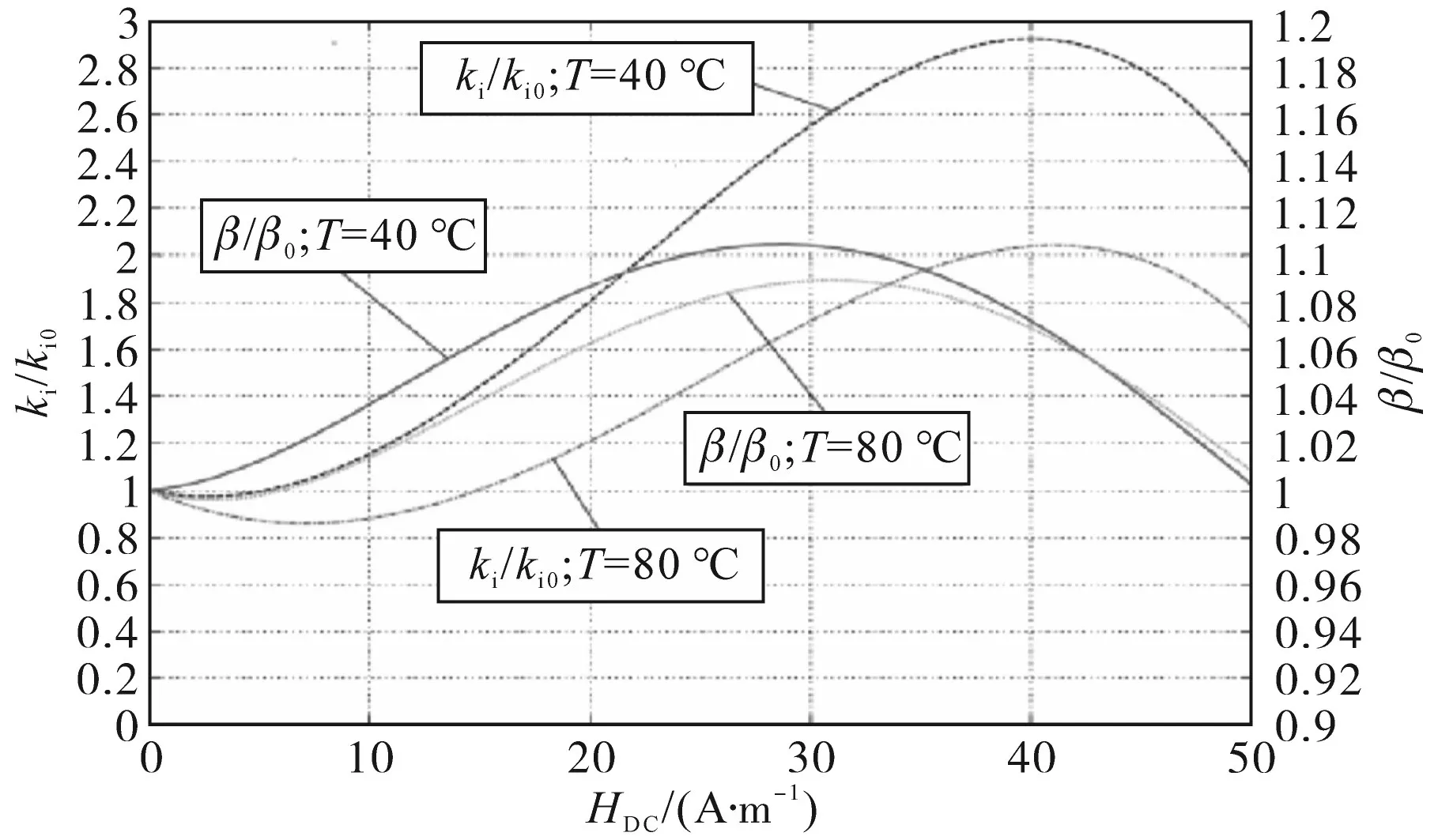
图3 铁氧体材料N87(EPCOS)Steinmetz参数图Fig.3 Steinmetz parameters graph of the material ferrite N87(EPCOS)
为了计算传导损耗,需要诸如场效应晶体管的导通电阻RDS,二极管压降VD,变压器一次和二次绕组电阻Rtp和Rts以及输出电感器电阻RL之类的数据。因此,在非对称控制模式下的总传导损耗描述为
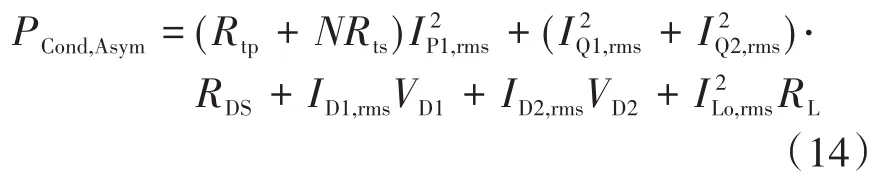
式中:IQ1,rms,IQ2,rms分别为开关 Q1,Q2的电流有效值;ILo,rms为输出电感的平均电流;IP1,rms为变压器一次侧的平均电流。
在非对称控制模式(PT,Asym)下,半桥转换器的总功率损耗为式(8)~式(11)及式(14)之和。
1.2 DCS控制模式下的功率损耗
此控制模式产生对称脉冲并消除IM,avg,并为其中一个开关提供软交换。DCS控制模式下半桥转换器的工作波形如图4所示。
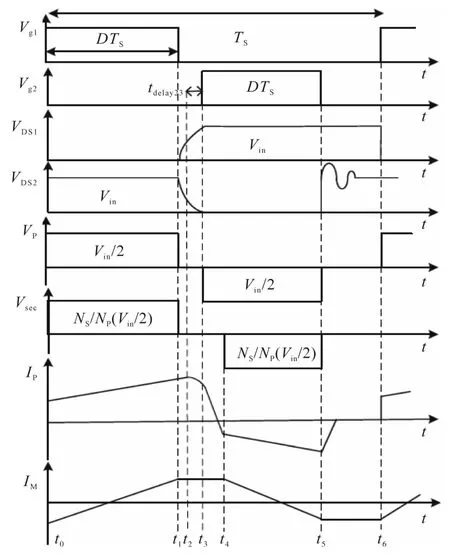
图4 半桥变换器在DCS控制模式下的工作波形Fig.4 Operation waveforms of half-bridge converter in DCS control mode
文献[13]中的等效电路描述了DCS控制模式下转换器的工作原理。如图4所示,对Q2栅极信号进行移位以调整Q1关闭和Q2开启之间的延迟时间,从而为Q2提供ZVS。在此模式下,由于占空比信号对称,IM,avg为零。Q1在t1时截止,IP对电容器C1充电并使电容器C2放电。由于变压器耦合,C2通过Lr和LO中存储的能量放电。C2完全放电后,Q2两端的电压达到零,并且Q2本体二极管在t3开始导通,并且Q2在ZVS条件下导通。在此控制模式下,Q1在硬开关条件下导通。Q1和Q2的开关损耗可通过代入式(7)中的开关的开、关电压和电流来得出,并表示为

此外,在此控制模式下,二极管的开关损耗计算如下:
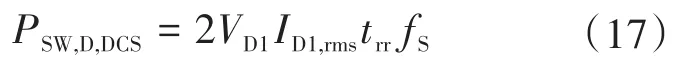
该控制模式下的磁芯损耗也由式(11)计算。由于HDC为零,因此Steinmetz参数是恒定的。在DCS控制模式下,半桥转换器的传导损耗计算如下:
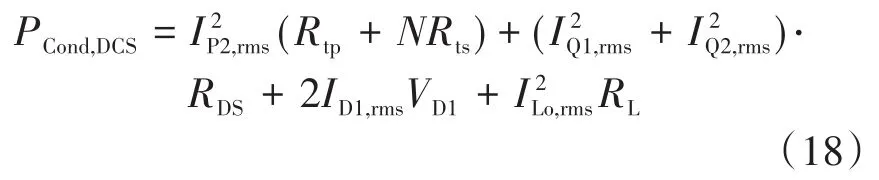
DCS控制模式(PT,DCSs)下的半桥转换器的总功率损耗为式(15)~式(18)及式(11)之和。
1.3 PWM控制模式下的功率损耗
在此控制模式下,将在硬切换条件下对称地打开和关闭开关。
PWM控制模式下半桥转换器的工作波形如图5所示。
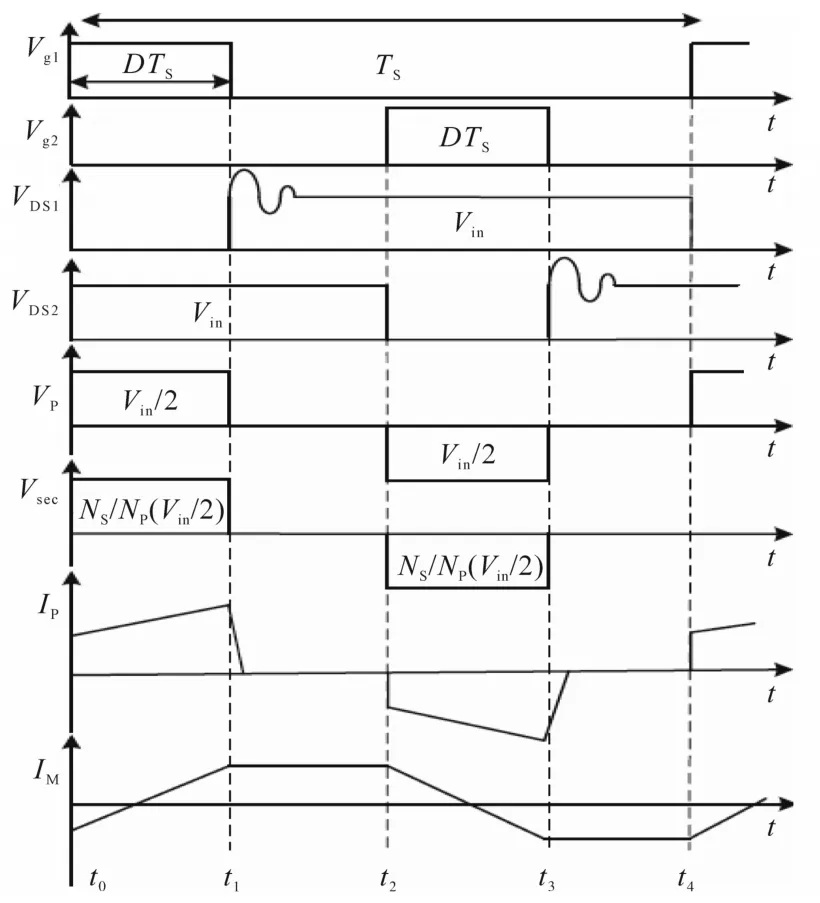
图5 半桥变换器在PWM控制模式下的工作波形Fig.5 Operation waveforms of half-bridge converter in PWM control mode
Q1和Q2的开关损耗相等,并通过代入式(7)中开关接通和关断时的电压电流来计算。

二极管开关和磁芯损耗与DCS控制模式下相同。
此外,在此控制模式下,半桥转换器的传导损耗由元件的电压和电流计算得出:
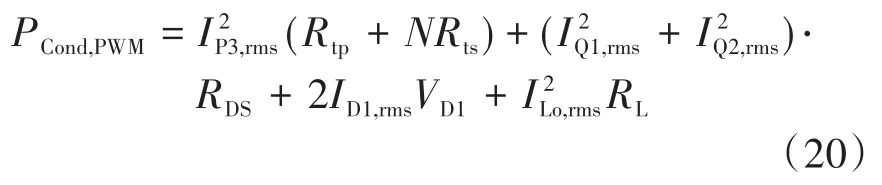
PWM控制模式下的半桥转换器的总功率损耗是式(19)、式(20)、式(17)和式(11)之和的两倍。
2 控制模式之间的过渡点
在本节中,将分别计算ITrans1,ITrans2和ITrans3三个过渡点。三个过渡点将整个负载变化范围分为四个子范围,分别称为“重负载”区、“半重负载”区、“轻负载”区和“超轻负载和空载”区。
2.1 过渡点的计算
确定过渡点时,不必比较四种模式的效率。换句话说,根据控制模式的特征,从满载到空载的优先级分别为非对称,DCS,PWM和突发控制模式。
在重负载条件下,由于非对称控制模式为两个开关都提供ZVS并显著降低了开关损耗,因此其效率优于为开关之一提供ZVS的DCS。此外,在重负载下,DCS优于PWM,后者在硬开关条件下均会导通。
根据式(5)的规定,通过降低负载,没有完全为其中一个开关提供ZVS,并且开关损耗增加。另外,IM,avg增加了磁芯损耗。这些因素降低了轻载条件下转换器的效率。将控制模式更改为DCS并消除IM,avg,可提高轻载条件下的效率。在非对称和DCS控制模式下转换器的效率变得相等的负载电流为ITrans1,其通过下式求得:

随着负载的减少,ZVS丢失了。同样,由于DCS中的电流有效值要比PWM高,因此导通损耗也更高。与PWM控制模式相比,这些因素降低了DCS控制中转换器的效率。因此,通过将控制模式改变为PWM,可以提高该负载条件下的效率。在这两种模式下,转换器的效率变得相等的负载电流为ITrans2,其通过下式求得:

从式(7)和式(11)可以看出,通过减小开关频率来减小开关和磁损耗。仅在超轻负载和空载条件下,才可以降低开关频率。突发控制模式用于减少超轻负载和空载条件下的开关损耗。在此控制模式下,两个边界用于调节输出电压。当Vo达到上限时,PWM被关闭;通过将Vo降低到下限,PWM被使用。在建议的控制方法中使用突发控制模式被设计为具有与PWM控制模式相同的输出电压波形。在突发控制模式下恒定波形电压的情况下,频率随着负载电流的降低而降低。然后,计算突发和PWM控制模式的输出电压波形相同时的最大负载电流,作为第三转换点ITrans3。PWM控制模式下转换器的输出电压波形计算如下:
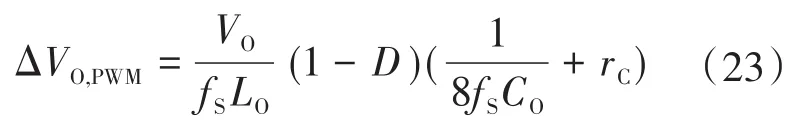
式中:rC为CO(ESR)的串联电阻。
另外,如文献[12]中那样计算突发控制模式下的输出电压波形。ITrans3通过下式求得:
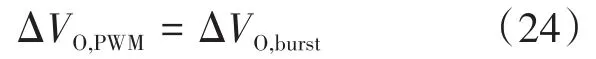
通过式(24)得到I0,则ITrans3=I0。式(21)、式(22)和式(24)通过数值方法求解。
2.2 参数变化对过渡点的影响
与式(21),式(22)和式(24)一样,转换器的参数(如RDS,COSS,Vin和fS)取决于过渡点的值。为了可视化这些效果,针对过渡点与参数生成了三维图。参数变化对过渡点的影响如图6所示。
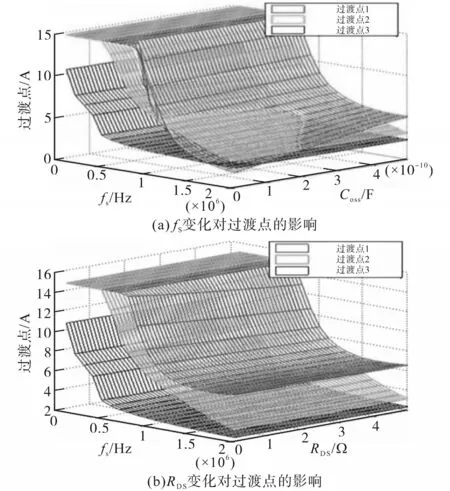
图6 参数变化对过渡点的影响Fig.6 Effect of parameters variations on transition point
图6a体现了过渡点相对于COSS和fS的变化。如图所示,当过渡点变化很大时,例如,在80 kHz和200 pF时,ITrans1,ITrans2和ITrans3分别为10.8 A,4.1 A和1.8 A,而在120 kHz和400 pF时,它们分别为8.7 A,3.8 A和1.6 A。在该图中,RDS为270 mΩ。
图6b体现了过渡点相对于fS和RDS的变化。在 80 kHz和 50 mΩ 时,ITrans1,ITrans2和 ITrans3分别为11.3 A,4 A和1.8 A,而在120 kHz和200 mΩ时,它们分别为9.7 A,3.8 A和1.6 A。在该图中,COSS为870 pF。
3 多模式控制方法
图7为所提出的多模式控制方法的流程图。数字控制器会定期采集负载电流,将负载电流与过渡点进行比较,并将转换器置于相关的控制模式下。
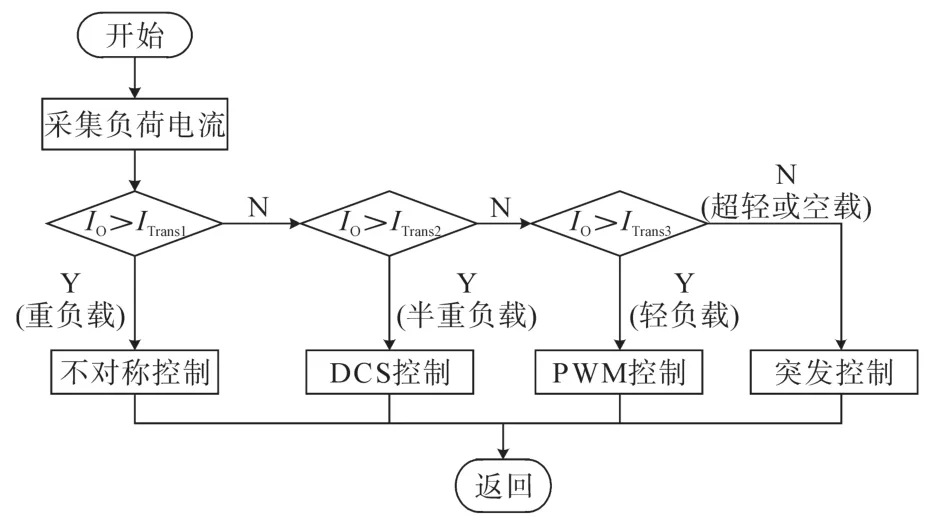
图7 拟定控制方法流程图Fig.7 Proposed control method flowchart
1)“重负载”条件和“不对称”控制模式:当负载电流高于ITrans1时,半桥转换器由不对称控制模式控制。在这种控制模式下,较高的磁芯损耗会导致在轻负载条件下效率降低。
2)“半重负载”条件和“ DCS”控制模式:此负载条件在ITrans1和ITrans2之间,并且半桥转换器由DCS控制模式控制,IM,avg为零,并提供ZVS开关。
3)“轻负载”状态和“PWM”控制模式:在负载电流介于ITrans2和ITrans3之间的情况下,半桥转换器由常规PWM控制模式控制。
4)“超轻和空载”条件和“突发”控制模式:半桥转换器由突发控制模式控制,负载电流低于ITrans3。如第2节所述,突发控制模式用于减少超轻负载和空载条件下的开关损耗。
4 测试设置和实验结果
图8为数控半桥转换器的实物平台。半桥转换器具有400 V直流输入电压,12 V直流输出电压,30 A输出电流和100 kHz开关频率。

图8 数字控制器和半桥变换器Fig.8 Implemented digital controller and half-bridge converter
本算例是根据文献[11−13]中的程序设计制造的半桥转换器。半桥转换器的电路参数如下:输出电感LO=32μH,输出电容CO=330μF,谐振电感 Lr=20 μH,MOSFET开启时间 tON=77 ns,MOSFET关闭时间tOFF=168 ns,MOSFET寄生电容COSS=870 pF,漏源电阻RDS=270 mΩ,二极管恢复时间trr=55 ns。转换器的组件为IRFP460A场效应晶体管,HFA50PA60C超快二极管,T40−14作为谐振电感器,T154−52作为输出电感器,EP⁃COS E42/21/20和N87用作变压器,变压器参数如下:Steinmetz参数中,α=1.57,β=2.5,k=20.02,变压器变比NP/NS=24/2,磁感应系数LM=1 650μH,磁路长度Ie=97 mm,初级匝数Ve=22 700 mm3。STM32F407处理器用作数字控制器,其参数如下:时钟频率168 MHz,ADC采样率2.4 MHz,数位分辨率12 bit,PWM分辨率16 bit。
选择开关和二极管时要考虑电压和电流应力。开关的最大电压和电流应力分别出现在PWM和非对称控制模式下,而对于二极管,这些最大值出现在非对称控制模式下。使用测得的输入和输出电压及电流绘制效率曲线。输出电压是固定的,输出电流从满载到空载都会变化。为了施加不同的负载电流,使用了滑动变阻器。输入和输出电流由GoodWill GCM−403数字钳形表测量。输入和输出电压由GoodWill GDM−357数字万用表测量。波形由GoodWill GDS−2074E数字示波器记录和测量。所有测试均在实验室的环境温度下进行,从满负荷到低负荷要经过15个步骤,大约需30 min。图9显示了效率曲线的实验结果。在图9中,显示了非对称对DCS,DCS对PWM,PWM对突发控制模式的效率曲线,其交点分别为8.4 A,4.5 A和2.1 A,分别对应了ITrans1,ITrans2和ITrans3。
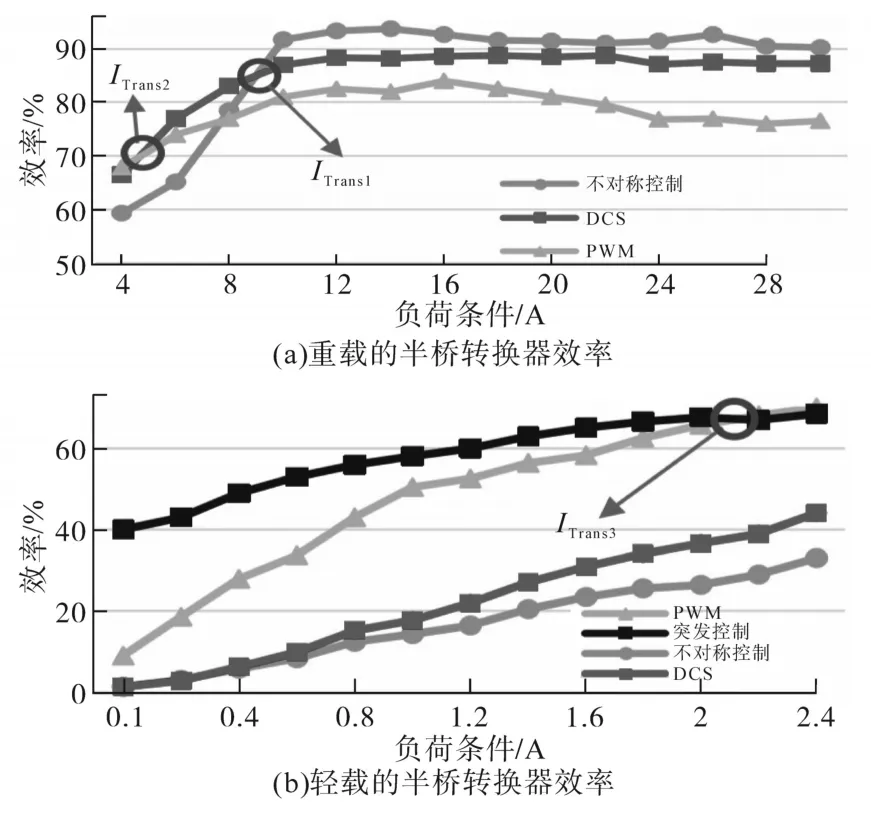
图9 半桥转换器效率的实验结果Fig.9 Experimental results of half-bridge converter efficiency
表1为过渡点使用式(21)、式(22)和式(24)得出的计算结果和实验结果,计算结果和实验结果相吻合,其差异可能是由于温度变化引起的制造公差和电路参数变化所致。因此,证明了本文所提的计算过渡点的方法非常精确,与通过实验得到的过渡点相比,差距很小。未来的研究中就可以用计算的方式得到过渡点,而不需要通过繁琐耗时的实验去获得过渡点,极大提高了研究效率。
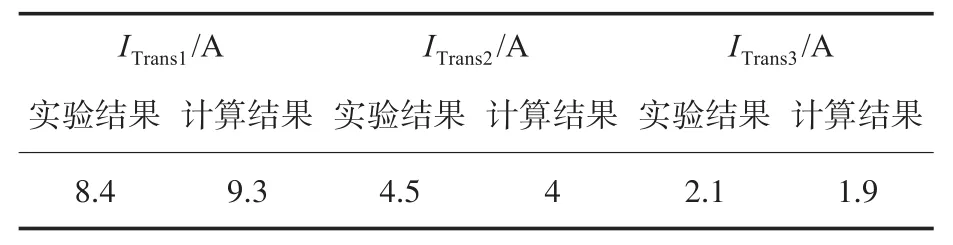
表1 转换器的计算结果和实验结果Tab.1 Calculated and experimental results of the converter
为了支持上述结论,本文开展多项实验,结果如表2~表5所示。
表2和表3显示了在不同频率和不同场效应晶体管下转换器的计算结果和实验结果的一致性。表4和表5中还描述了输入和输出电压变化对过渡点的影响。
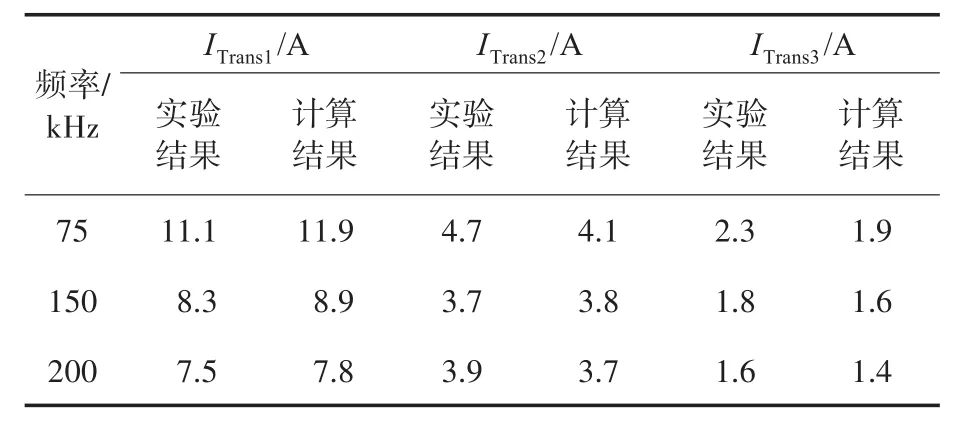
表2 不同频率下变换器过渡点的计算与实验结果Tab.2 Calculated and experimental results of the converter transition points at different frequencies
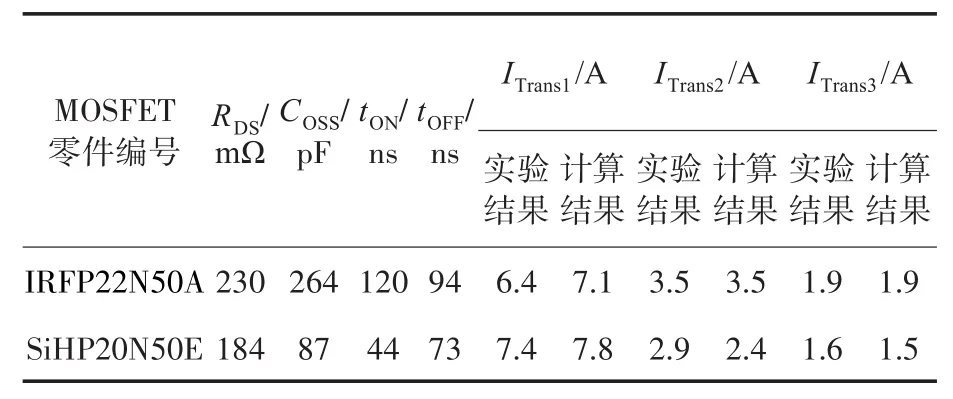
表3 其他场效晶体管在100 kHz下的计算结果和实验结果Tab.3 Calculated and experimental results with other MOSFETs at 100 kHz
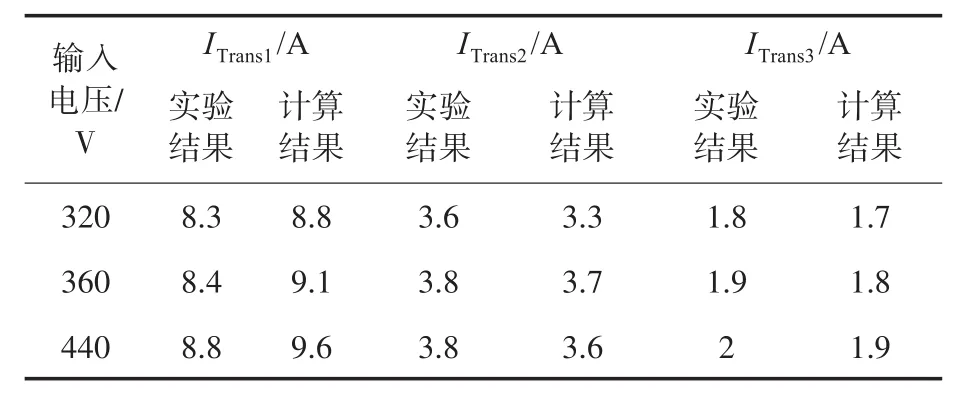
表4 不同输入电压下过渡点的计算结果和实验结果Tab.4 Calculated and experimental results of transition points at different input voltages

表5 不同输出电压下过渡点的计算结果和实验结果Tab.5 Calculated and experimental results of transition points at different output voltages
数字控制器使用磁滞回路将负载电流与转换点进行比较,以消除任意两个相邻控制模式之间的跳动。控制模式之间转换性能的实验结果如图9所示。可以看出,在控制模式转换期间,半桥转换器的输出电压保持恒定。图10显示了所提控制策略和非对称控制的转换器的动态响应,包括过渡和稳定时间。
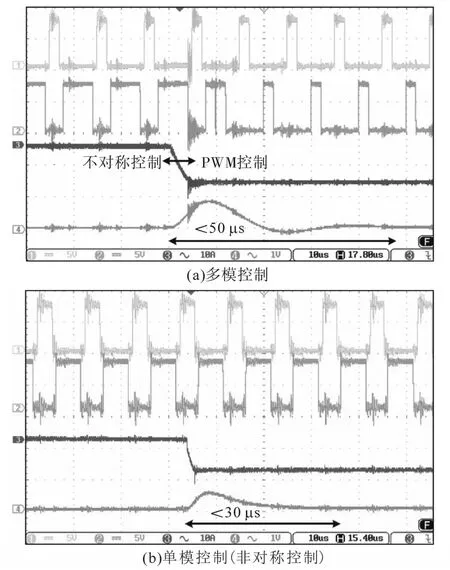
图10 动态响应实验结果Fig.10 Experimental results of dynamic response
此外,对于所提出的控制方法和非对称控制,从空载到满载的转换器的实验结果如图11所示,可以看到,对于所提控制策略,稳定时间和下冲为400μs和1.2 V。非对称控制分别为360μs和1 V。为了衡量所提出方法的节电措施,进行对比实验,结果如图12所示,利用图9中的效率曲线可以计算不同控制方法的24 h总功耗。对于非对称、DCS和PWM控制模式,该方法的节电量分别为19 W(6.3%),26 W(8.4%)和32 W(10.2%)。采用所提控制策略,并分别采用计算过渡点和实验过渡点进行功耗计算。如图12所示,相对于其他控制模式,所提策略极大降低了功耗,并且采用计算过渡点产生的功耗仅比实验过渡点产生的功耗多3 W(1%)。
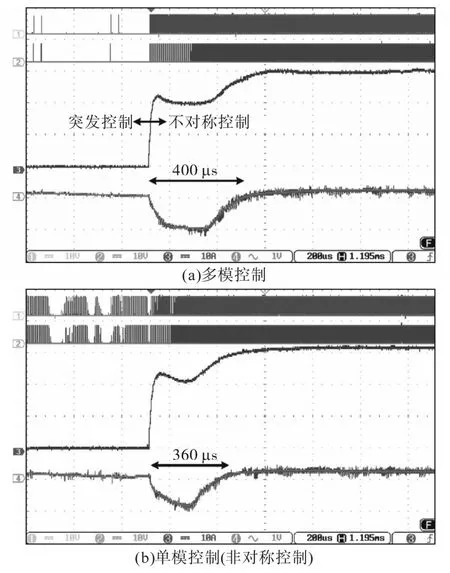
图11不同控制模式下从空载到满载的实验结果Fig.11 Experimental results from no load to full load under different control modes
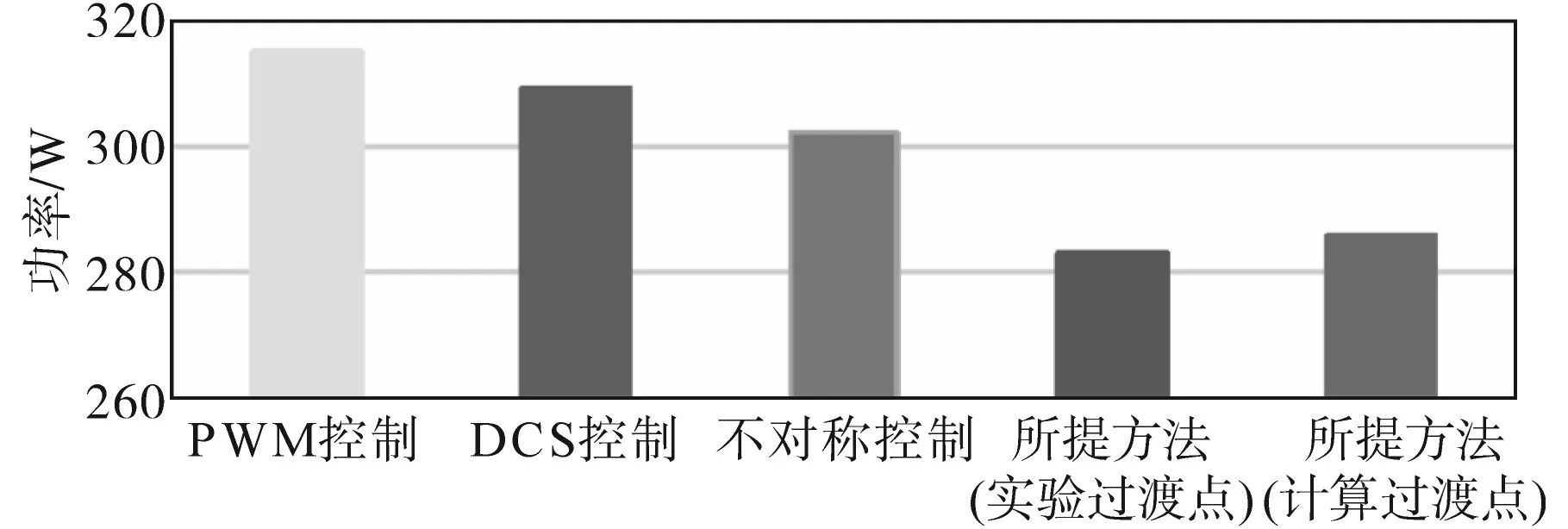
图12 不同控制方法对变流器的24 h功耗的比较Fig.12 Comparison of 24 h power consumption of the converter using previous and proposed control methods
5 结论
本文针对半桥变换器的四种主要控制模式,提出了一种多模式切换控制方法。这些模式是:非对称,DCS,PWM和突发控制。并将负载电流变化范围分为“重负载”、“半重负载”、“轻负载”及“超轻负载和空载”四个区域。基于变换器功率的损耗分析,结果表明能够以足够的精度计算出作为变换器电路参数的控制模式之间的过渡点。另外该方法提高了半桥转换器的效率。为了验证上述结论,本文进行了多项实验,结果证明,所提出的控制方法优于先前的控制方法,并且所计算的过渡点足够准确,可以用计算结果来替代耗时的实验方法。

