集群LED路灯谐波与超高次谐波的发射特性研究
谢荣斌,林义泽,闫东辉,周群 ,曹庆
(1.贵州电网息烽供电局,贵州 息烽 551100;2.四川大学电气工程学院,四川 成都 610000)
近年来,环保与资源形势日益严峻,采用高效节能灯具是降低能耗的重要举措之一。LED与白炽灯相比LED功耗远远低于白炽灯,同时具有电光转化效率高(接近60%)、寿命长(可达10万h)、工作电压低(3 V左右)、易于调光、色彩多样、光束集中稳定、启动无延时等诸多优点,使得LED灯具得到了成规模的应用[1]。
但随之而来的是一系列新的问题,其中最突出的便是由LED驱动引发的谐波问题。对于大功率的照明灯具国际上已经颁布了IEC6100—2—3谐波排放标准,但是该标准只对39次及其以下的谐波排放做出了相应的规定,如表1所示,但是频率在2~150 kHz范围内的超高次谐波并无国家或行业范围内的相关标准[2−5]。
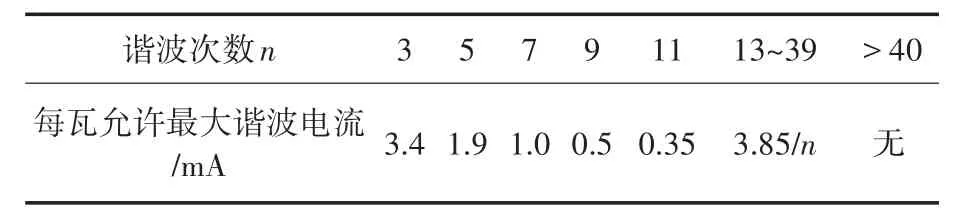
表1 IEC6100—3—2谐波排放标准Tab.1 IEC6100—3—2 harmonic emission standards
LED路灯驱动电路网侧多采用整流桥加Boost-PFC结构,其产生的2 kHz或40次以下的谐波虽然能满足IEC6100—2—3中对照明设备的谐波排放标准[5−8],但是对于2 kHz及其以上的超高次谐波而言,缺乏相关标准限制。虽然单盏LED路灯所排放的谐波量较小对电网不会造成影响,但是在低压配电网中存在大量的LED路灯,其排放的谐波和超高次谐波总量不容小觑,会对电网及连接在电网上的用电设备造成一定程度的危害[8−12]。
目前有少量文献对集群LED路灯的谐波问题做了分析,但是都只分析了40次及其以下的传统谐波。配电网络作为与用户直接相连接的电力网络,有着电压等级低(220 V~10 kV)、线路分布广、电气设备多等特点,大量的非线性负荷排入配电网中的40次以上的超高次谐波会对临近的电气设备造成危害,同时会影响与配电网相连接的高精度用电仪器的精度[13]。因此本文旨在分析低压配网中的集群LED路灯排放的谐波和超高次谐波,为进一步制定集群LED路灯的谐波排放标准和对低压配电网谐波的治理提供参考依据。
1 LED路灯的驱动电路结构
典型的大功率LED路灯驱动电路模型如图1所示。该模型由220 V交流电源、整流电路、滤波电路、Boost-PFC校正电路、Buck(降压)电路和LED构成。其中整流电路将网侧220 V交流电流变换为直流电流;Boost-PFC校正电路在将电压提升的同时将电流波形校正到接近正弦波形状从而提高电路的功率因数;Buck电路为LED提供稳定的直流驱动电流。
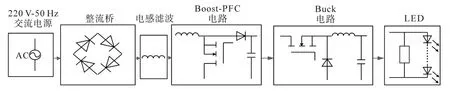
图1 LED驱动电路模型Fig.1 The model of LED drive circuit
从图1中可以看出,该型号LED路灯网侧低次谐波电流的谐波主要与整流电路和滤波电路有关,因此在分析网侧电流表达式时,将滤波电路之后的电路按照功率守恒的原则,近似等效为电阻R。因此该LED驱动电路等效模型如图2所示。
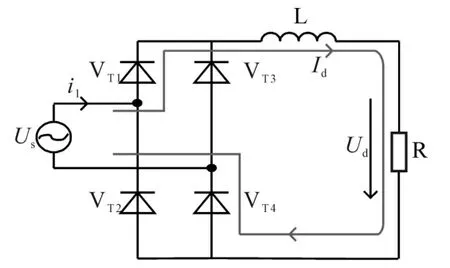
图2 LED驱动电路等效模型Fig.2 Equivalent model of LED driving circuit
等效模型的输入电流表达式推导过程如下:
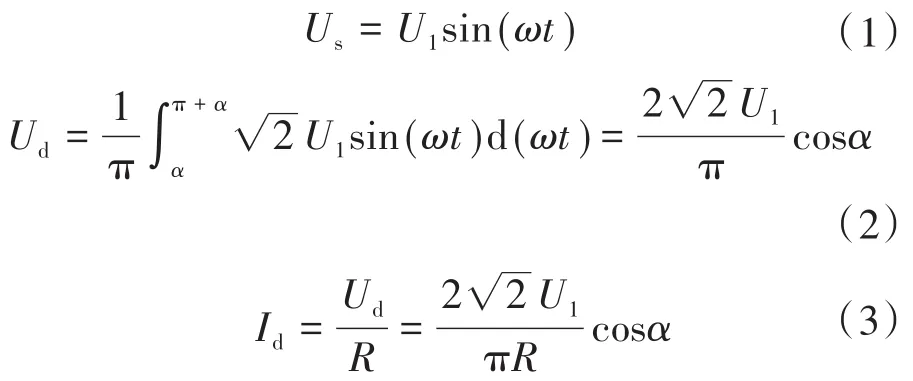
式中:Ud为半个正弦周期内二极管上的电压;Id为半个正弦周期内流经二极管的电流;α为二极管初始导通角;ω为角频率;R为等效电阻;U1为电源电压有效值。
由功率守恒得:

式中:P为LED路灯的功率。
因为负载为阻感性,因此初始导通角为[14]
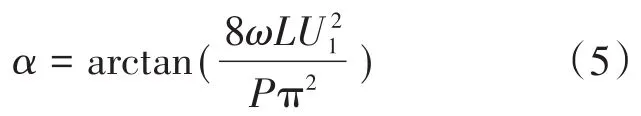
由于二极管在正弦电源的半个周期内成对导通,因此网侧谐波电流表达式如下:

i1是周期为2π的周期函数,根据傅里叶级数分析,可将其分解为傅里叶级数叠加的形式:
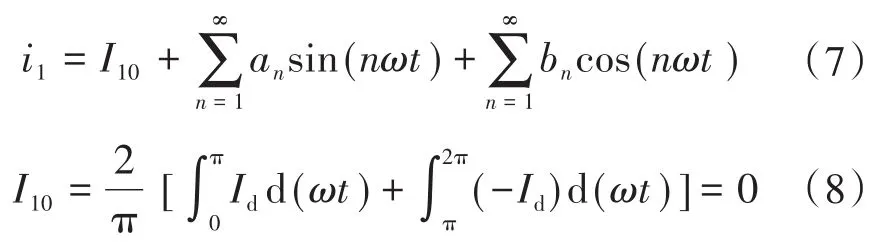
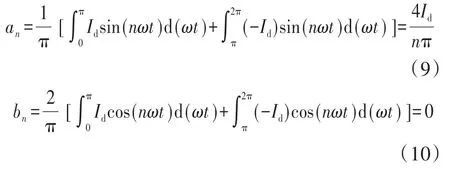
因此LED路灯网侧电流表达式为
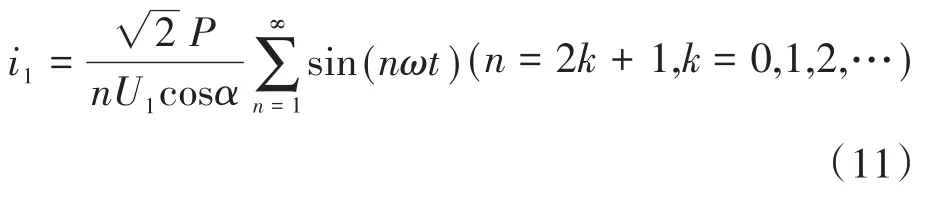
2 集群LED路灯的谐波和超高次谐波特点分析
2.1 谐波特点分析
由于低压配电系统的等值阻抗一般呈感性,谐波等值电抗随谐波次数的升高而增大,谐波电流将随谐波次数的升高而迅速衰减。因此在低压配电系统里传统意义上的谐波是指0~2 kHz范围的谐波,此类谐波在低压配电系统中的含量最多。而LED路灯作为低压配电系统中最常见的一类非线性负荷,其网侧的电流表达式如下:
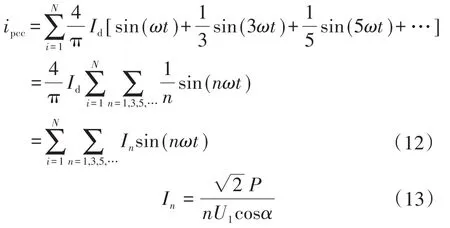
式中:i为LED路灯数量;Id为流过二极管的电流;n为谐波次数;In为基波和各次谐波的有效值。
由于多个LED路灯并联,电流的相位会产生相互影响,因此式(12)是在不考虑LED路灯相互影响的理想情况下得出的多盏LED路灯工作时其PCC处的电流标量之和。由式(12)可见电流中仅含奇次谐波,各次谐波有效值与谐波次数成反比,且随着LED功率的增大,其各次谐波电流也增大。
2.2 超高次谐波特点分析
为了降低0~2 kHz范围内的较低次谐波,在LED路灯驱动电路中采用了新型快速电力电子开关器件,以减小死区幅度校正电流波形到接近正弦状态从而提高功率因数。但是较高的开关频率随之带来了一些新的问题,其中超高次谐波(2~150 kHz)就是最典型的问题。LED路灯网侧的超高次谐波电流有效值如下式所示[15]:
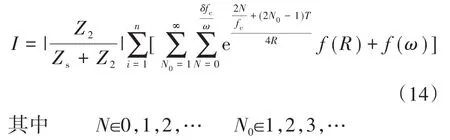
式中:Zs为系统阻抗;Z2为滤波电路等效阻抗;N为迭代计算产生的变量;N0为电网电压公频倍数;fc为开关频率;T为电网基准电压周期;R为Buck电路的等效电阻;ω为系统基准电压频率;i为LED路灯数量;δ为整流电路导通角。
由式(14)可以看出,当LED路灯驱动电路参数确定后,其超高次谐波电流的有效值主要受到开关频率、系统阻抗和LED路灯数量的影响。图3为LED路灯所产生的超高次谐波电流与系统阻抗和LED驱动电路自身阻抗之间的关系,随着系统阻抗的增加,超高次谐波电流含量减少,但是随着LED自身阻抗的增加,超高次谐波电流含量增加。
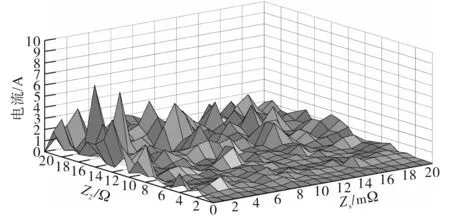
图3 阻抗与超高次谐波电流关系图Fig.3 Relationship between impedance and super harmonic current
当多个设备共同作用时,其超高次谐波电流之间存在一次发射和二次发射现象,超高次谐波电流会在设备之间流动,从而对流入电网中的超高次谐波含量造成影响[16]。为了研究公共连接点处的超高次谐波特性,建立等效电路模型如图4所示。图4中,I1,I2,…,IN分别为N盏LED发射的超高次谐波电流有效值;Z1,Z2,…,ZN分别为N盏LED的等效阻抗;Zs为电网等效阻抗。
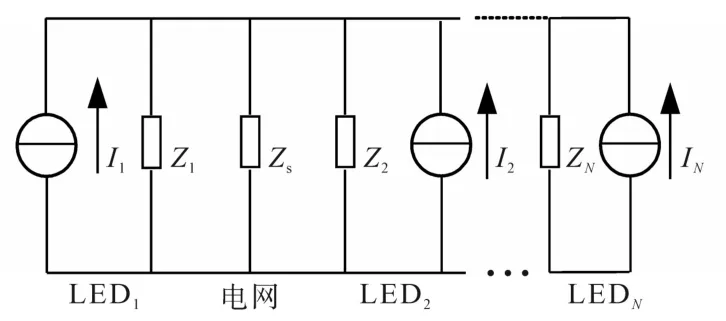
图4 集群LED路灯等效电路模型Fig.4 Equivalent circuit model of cluster LED street lights
集群LED路灯等效阻抗如下所示:

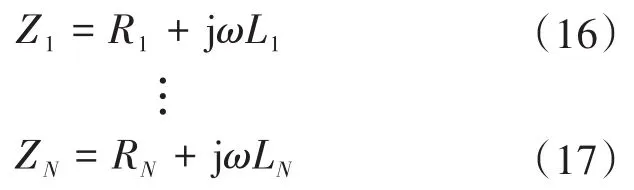
式中:Rs,Ls分别为电网的等效电阻和电感;R1,L1分别为第1盏LED的等效电阻和电感;RN,LN分别为第N盏LED的等效电阻和电感。
当考虑LED1的一次发射电流和终端超高次谐波电流时,其它LED路灯的超高次谐波电流、阻抗和电网阻抗三者可以近似等效为一个电压源和阻抗的串联,等效图如图5所示。
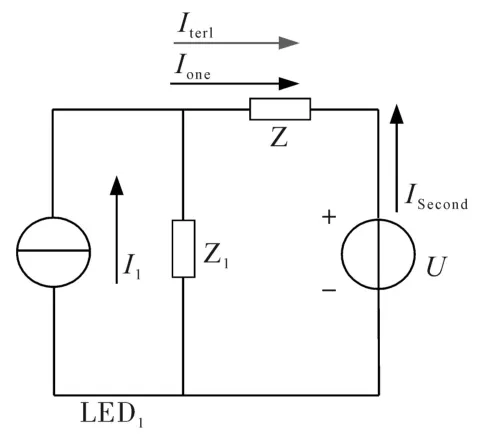
图5 LED路灯超谐波等效图Fig.5 Equivalent diagram of LED street light superharmonic
图5中:

一次发射电流为

二次发射电流为
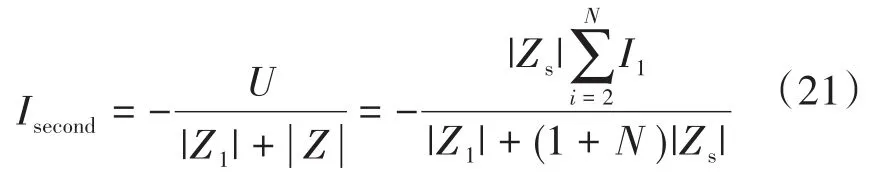
LED1终端超高次谐波电流为
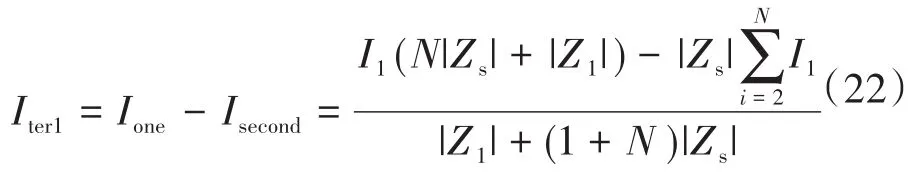
流入电网的超高次谐波电流Ipcc为
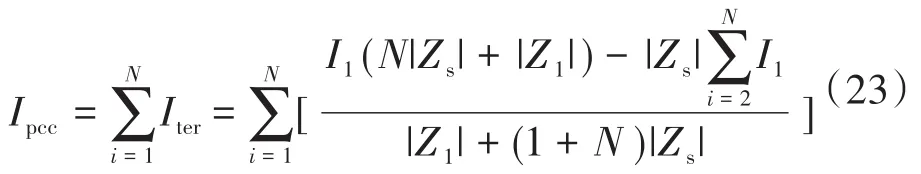
可以推出:

式中:Iter为单盏LED网侧超高次谐波电流含量。
由式(23)可以看出流入电网的超高次谐波电流与系统等效阻抗、LED等效阻抗、单盏LED超高次谐波电流和LED路灯数量有关。由式(24)可看出,当不考虑系统阻抗时(Zs=0)流入电网的超高次谐波电流Ipcc等于每盏LED路灯的超高次谐波电流之和。当考虑系统阻抗时(Zs≠0)流入电网的超高次谐波电流Ipcc要小于每盏LED路灯的超高次谐波电流之和。
3 仿真与实测分析
3.1 仿真模型
为了更好地对低压配网中的集群LED的谐波和超高次谐波发射特性进行分析同时对上述理论分析进行验证,根据实际线路情况(1.5 km路灯线路)搭建仿真模型。根据《配电网技术导则》和所选测量线路具体情况(LGJ−10/2),计算出该路灯线路的平均分布阻抗参数为R=2.706 Ω,L=10 H。表2为该条线路上所使用的LED路灯参数,该条线路上有此类LED路灯20盏。对此路灯线路建立仿真模型如图6所示。

表2 LED路灯参数Tab.2 LED street light parameters

图6 集群LED路灯仿真模型Fig.6 Simulation model of cluster LED street light
3.2 仿真结果及分析
图7为理想情况下(不考虑系统阻抗)集群LED路灯的电压电流波形图,从图7中可以看出其电压波形有良好的正弦度,其电流波形存在一定程度的畸变且有死区问题(过零点时短暂时间内电流幅值为零)存在。图8为电流频谱图,从图8可以看出其谐波电流主要分布在0~2 kHz,2~10 kHz和49~51 kHz三个频段内。在低频段(0~2 kHz)内谐波电流只含有3,5,7等奇次谐波且随着频率升高其占比迅速减小。在高频段(2~10 kHz和49~51 kHz)内谐波电流也只含有奇数次谐波但是其含量并不随次数的升高而降低,在频率50 kHz附近时(LED路灯开关频率)其谐波电流含量迅速上升。
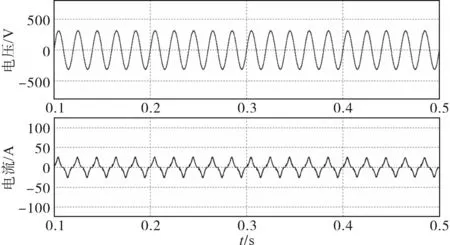
图7 不考虑系统阻抗的电压电流波形图Fig.7 Voltage and current waveforms without system-impedance
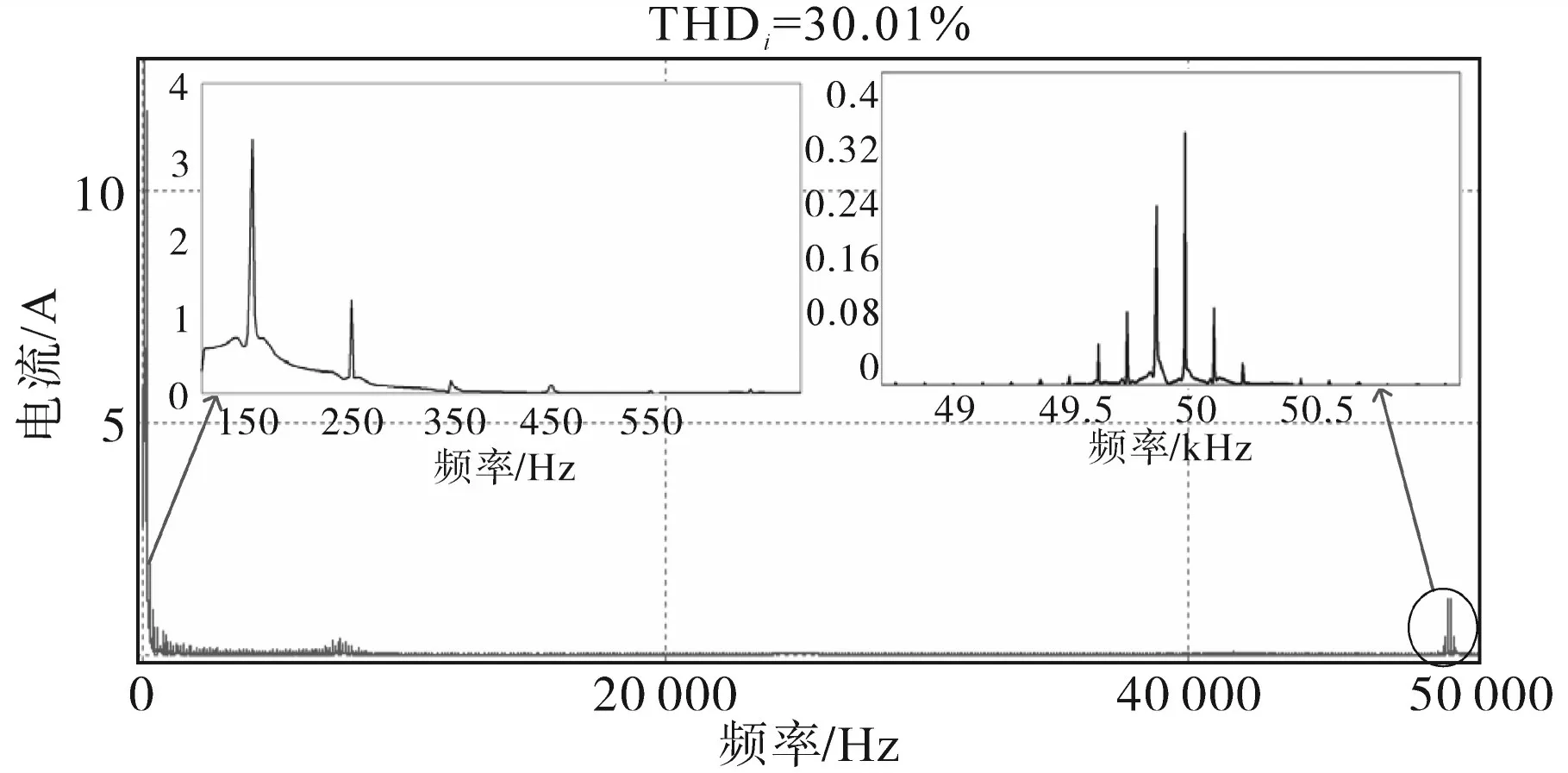
图8 电流频谱图Fig.8 Current spectrum
图9为考虑系统阻抗情况下的集群LED路灯的电压电流波形图,从图9中看出其电压波形没有畸变,电流波形畸变严重。图10为电流频谱图,在考虑系统阻抗情况下其谐波电流在低频段(0~2 kHz)内3次和5次谐波电流含量较高,且随着谐波次数升高谐波电流迅速减小。在高频段(2~10 kHz和49~51 kHz)内其谐波电流含量明显降低。此现象和上文超高次谐波产生机理及公共连接点处的超高次谐波特性相吻合,说明超高次谐波含量与系统阻抗有密切关系。
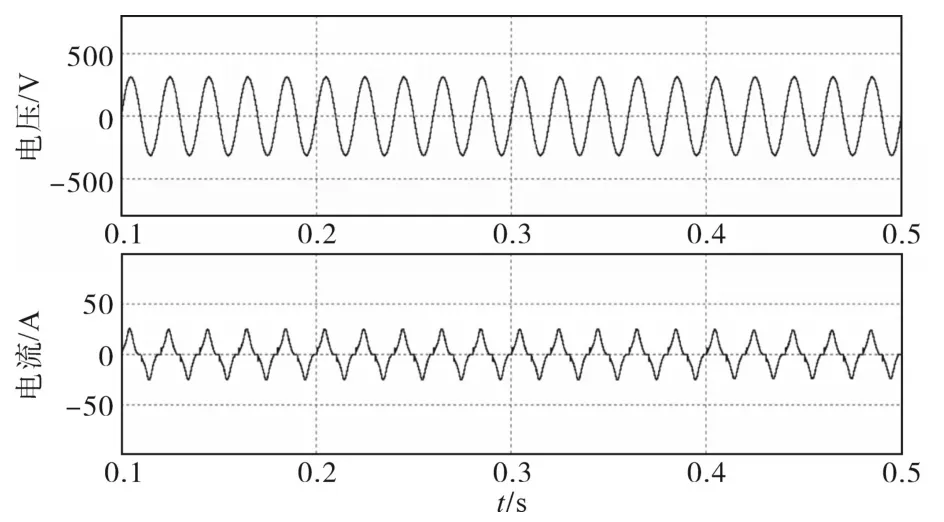
图9 考虑系统阻抗的电压电流波形图Fig.9 Voltage and current waveforms with system-impedance
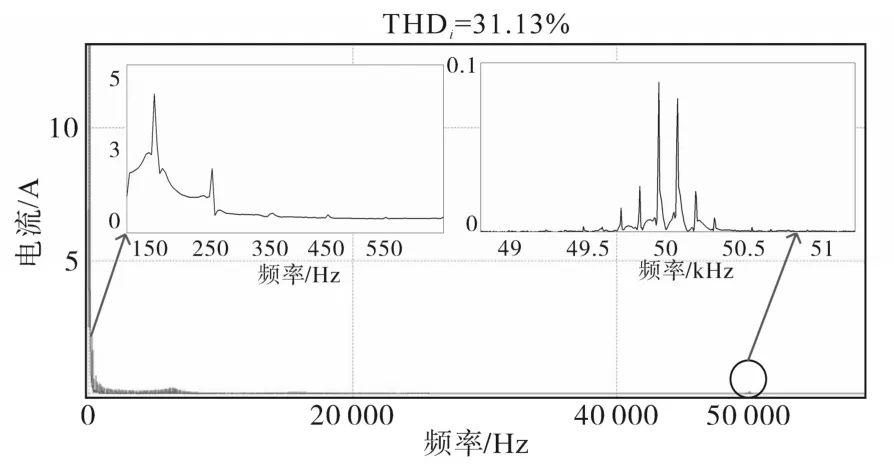
图10 电流频谱图Fig.10 Current spectrum
表3为低压配电网中奇次谐波限制与仿真情况的对比,可以明显看出其3次谐波电流含量远远超出电网允许值,5,7,9次谐波电流含量在允许范围内。其超高次谐波电流值大于等于0.6 A但是低压配电网中目前并未给出相应的谐波排放限制。
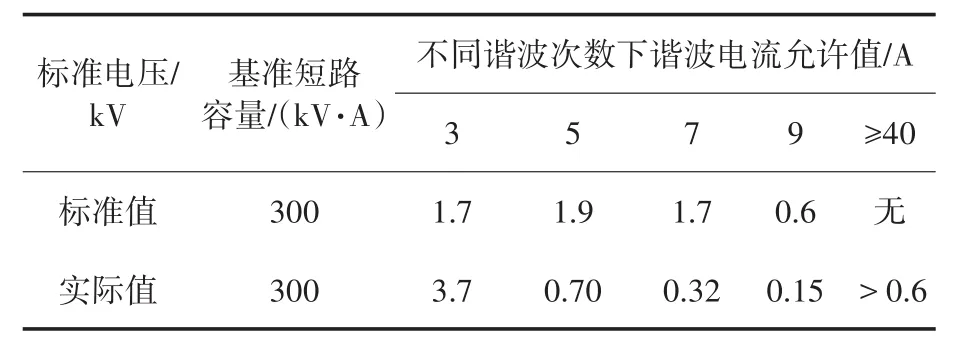
表3 380 V电网谐波电流对比表Tab.3 380 V grid harmonic current comparison table
图11为LED路灯数量与频率50 kHz附近的超高次谐波电流含量的趋势图,从趋势图中看出,当不考虑系统阻抗时流入电网的超高次谐波电流含量近似等于单盏LED路灯的超高次谐波电流之和。当考虑系统阻抗时流入电网的超高次谐波电流含量随着LED路灯数量的增加而增加,但是其增加趋势并不是简单的累加结果,而是随着路灯数量的上升,其增加趋势明显变得相对平缓。当路灯数量增加到一定程度时,其超高次谐波电流增加缓慢,因此说明在实际电力网络中(Zs≠0)超高次谐波电流之间的叠加不是标量叠加,而是矢量叠加,同时也反映出超高次谐波电流之间有一定的抵消机制,同时上述现象也验证了式(23)所分析的准确性。

图11 超高次谐波电流与LED路灯数量关系Fig.11 Relationship between superharmonic current and number of LED
3.3 实测结果及分析
为验证上述理论推导和仿真结果的准确性,对国家电网某供电局所属一条长1 km的路灯线路(20盏LED路灯,工作原理如图1所示)进行周期性测量。
测试仪器为:FLUKE435电能质量测试仪(低次谐波测量)、录波仪(由于FLUKE435电能质量测试仪只能测低次谐波,因此在研究超高次谐波时采用录波仪记录波形后导入Matlab软件进行分析)。
测试周期为16 h(路灯工作时长为10 h)。
图12为用电能质量测试仪测得的该条LED路灯线路的电压与电流波形图,从图12中看出其电压波形呈正弦波形状,且畸变率为2.42%满足低压配电网电压谐波排放标准(<5%)。但是电流波形存在严重的畸变,含有较多的超高次谐波成分,并且在每个周期内有死区现象存在(过零点时短暂时间内电流幅值为0)与仿真结果相吻合。

图12 LED路灯线路电压电流波形图Fig.12 Voltage and current waveforms of LED street light
图13为使用电能质量分析仪对该条LED路灯线路进行时长为16 h的电压电流情况监测得到的畸变率,发现当LED路灯打开时(20∶00时刻)其电压畸变率从1.6%上升到2.6%一直持续到LED路灯关闭(次日5时30分),同样的时间段内其电流畸变率从19%上升到33%。图14为其电压电流FFT(快速傅里叶分解)后的谐波含量,可以看出在低频段内电压只含有奇次谐波,且7次谐波含量最多,电流也只含有奇次谐波成分且随着谐波次数升高其含量逐渐降低。图15为该条LED路灯线路的电流频谱图(将录波仪中的数据导入到Matlab中分析),其谐波主要分布在低频段(0~2 kHz)和超高次频段(2~10 kHz,50 kHz附近)。表4为该条线路的3,5,7,9和1 000次谐波电流含量值。从上述测试结果中看出实测值近似等于仿真结果和理论推导,从而证明了理论推导和仿真模型的准确性。

图13 LED路灯线路电压、电流畸变率Fig.13 LED street light line voltage and current distortion rate
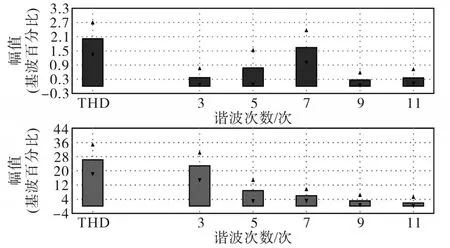
图14 电压电流FFT图Fig.14 Voltage and current FFT diagram

图15 电流频谱图Fig.15 Current spectrum
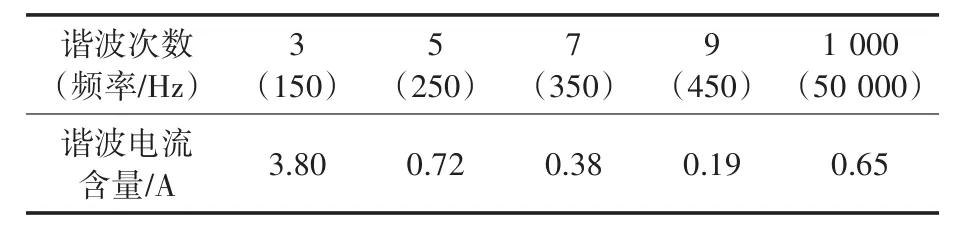
表4 谐波电流实测值Tab.4 Harmonic current measured values
4 结论
本文通过理论计算和仿真实测的方式,对集群LED的谐波和超高次谐波发射特性进行了评估,发现集群LED对低压配电网的电压造成的影响很小几乎可以忽略。但是会使低压配电网的电流波形造成严重的畸变,其谐波电流主要有以下特征:1)在低频段内谐波主要为奇次谐波且随着谐波次数的升高谐波电流含量降低;2)超高次谐波(2~150 kHz)主要为奇数次谐波,在50 kHz(开关频率)附近含量较多;3)超高次谐波含量与低压配电网系统阻抗和LED路灯数量之间有着密切关系,当考虑系统阻抗时超高次谐波含量要小于不考虑系统阻抗的情况,超高次谐波含量随着LED路灯数量的增加呈现矢量叠加效果,存在一定的抵消机制。

