基于并行SIMT 平台的电网系统造价数据分析研究

郭嘉成，宋妙环，王炳文

（国网甘肃省电力公司经济技术研究院，甘肃兰州 730050）

电网工程的建设包括决策设计、施工与管理等步骤，是一个大型的系统工程[1]。每个步骤的顺利实施均建立在对电网工程准确分析的基础上[2]，而电网工程的造价数据影响因素多[3]、数据量大，导致对其精细分析的难度较高[4]。目前的分析与验证大量消耗了运行时间和内存，同时可优化的程度较低[5]。

基于大规模并行单指令多数据（SIMD）或是基于单指令多线程（SIMT）的GPU 平台的出现，为大规模电网数据分析提供了良好的解决方案[6]。目前的商用GPU 可以提供超过380 G的浮点运算能力和86 GB/s的片外内存带宽，是现代通用四核微处理器的3～4 倍。文中基于SIMT GPU，设计了一套电网工程造价数据的分析系统[7]。

1 系统造价数据建模

假设建造者的资源有限，减少总预算的一种方法是将预算分配给选定的线路，以增加其建造成本。将系统预算定义为m行的元组数据，每行l均有自身的预算成本函数，由dl(bl)描述。函数dl(bl)表示当预算bl部署在生产线上时，生产线l的额外建造成本。

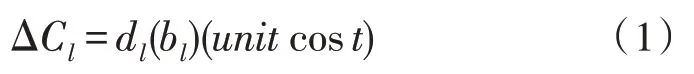
因此，第l行的建造成本可以表示为：

其中，Cl,0是第l行的初始建造成本。

函数dl(bl)应根据l行的实际预算成本特征来制定，通常应符合以下条件：

1）当bl=0，dl(bl)=0；

2）当bl=∝，dl(bl)=∝；

3）dl(bl)是单调递增函数。

尤其是当部署了足够的预算来建造l行时，建造成本变得无限大，建造者必须具有足够的建造能力才能成功建造该行。

假设一个建造计划包括m条线，建造成本分别为C1,…,Cm，建造者的建造能力为R。

若建造者可以成功执行建造计划，则必须满足以下条件：

从预算节省的角度来看，若预算审批者旨在优化建造计划，则应将预算部署到计划中的一组上。从而使计划的建造成本大于R，即：

因此，预算审批者的目标是减少电力系统的建造预算损害，将建造预算限制在预期水平。为了解决该问题，预算审批者必须找到满足以下两个条件的所有线组合：

1）建造成本小于R；

2）预期收益效果必须大于给定值LS。

满足以上两个条件的任何线组合，均被定义为预算优化的候选线组合。

因此，预算部署模型可以公式化为以下非线性优化问题：

限制条件为：

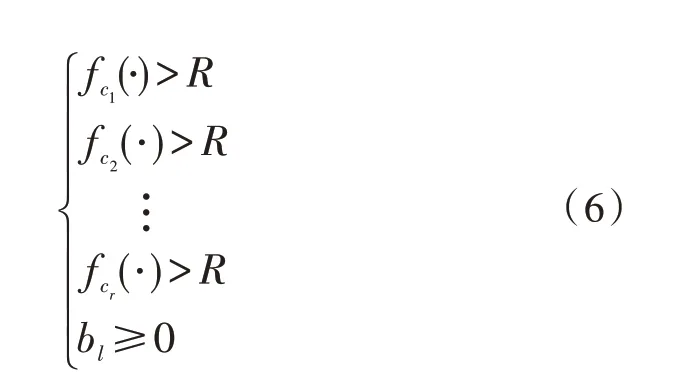
其中，fcr(·) 表示第r个候选行组合的建造成本。通过引入一个小的正常数R0，可以进一步将式（6）转换为以下形式：

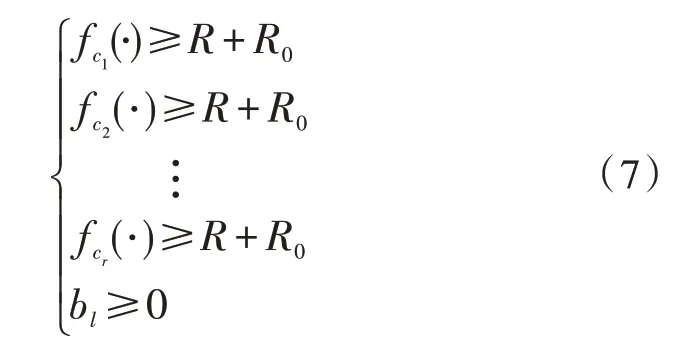
对于式（5）与式（7）所示的预算分配问题，使用改进的蛮力搜索算法枚举所有候选行组合。然后基于候选线组合来制定预算部署问题，最终通过原始对偶内点法解决该问题，并确定最佳预算部署策略。预算优化分析流程如图1 所示。

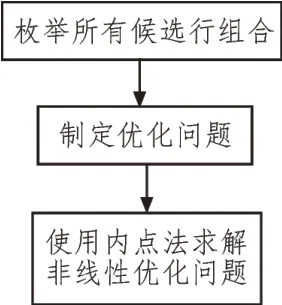
图1 预算优化分析流程

预算审批者的目的是将建造成本限制在预期水平LS内。为了实现该目标，预算审批者必须找到所有候选的线路组合并部署预算，从而优化建造成本。

首先确定可行的建造集A，其中包括所有建造成本小于R的线组合。这样，由于丢弃建造成本大于R的线组合，从而减小了搜索空间。

接下来在可行建造集合A中找到所有候选行组合，使用两种措施来加快搜索过程。

措施1：确定最小行数NAmin。忽略行数小于NAmin的组合，以减少搜索空间。使用双层模型来解决该问题，无需考虑线性规划的线建造成本。基于上述工作，将线建造成本约束引入模型中以计算NAmin。

措施2：定义PL是候选行组合。即任何线路组合PL+ΔPL均可自动视为冗余线路组合，这是因为预算部署会使线组合PL的建造成本增加到高于R；而预算部署会自动增加线组合PL+ΔPL的建造成本超过R。因此，无需部署预算来支持多余的候选行组合PL⋃ΔPL。

2 并行SIMT运算系统设计

由于电网工程的复杂性，导致建立式（7）所示的优化模型过于庞大，单线程的数据处理方法难以迅速处理，因此设计了基于并行SIMT的数据预算系统[8]。

要在SIMT 平台上实现最佳的分析效率，充分了解实际电网系统造价涉及的物理特性至关重要[9]。可以预期，若可以类似于像素图形一样存储与处理电网工程数据[10]，则GPU SIMT 平台将比通用CPU 平台具有显著优势[11]。因此，文中考虑求解一个接近原始栅格的近似规则电源栅格[12]。

2.1 基于GPU的几何多重网格方法

几何多重网格方法是解决大型造价数据优化问题的最快数值算法之一，其中创建了给定线性问题的层次结构[13]。通过迭代更新，分别在细网格和粗网格上迅速衰减求解错误的高频分量与低频分量，从而提高多重网格的效率。经过适当设计，多重网格方法可以实现未知数线性复杂度。由于GPU 片上共享内存有限，因此多重网格的分层迭代性质对GPU 平台具有较为重要的意义[14]。多网格方法通常分为两类：几何多网格（GMD）和代数多网格（AMG）[15]。若可以利用问题的特定几何结构，则AMG 可以被认为是一种鲁棒的黑箱方法[16]，虽然初始化代价较大，但GMD 可以更有效率地实现。该次的多重网格关键操作包括：

1）平滑：采用迭代方法Gauss-Seidel 来缓解网格上的求解误差；

2）限制：从细网格映射到下一个较粗网格（用于将细网格残差映射到粗网格）；

3）延长：从粗网格到下一个较细网格的映射（用于将粗网格解映射到细网格）；

4）校正：使用映射的粗网格解决方案来校正细网格解决方案。

在具有vk初始解的第k级网格上，多网格循环MG(k,vk)步骤如下：

1）应用预平滑更新解决方案；

2）计算第k个网格上的残差，并通过限制将其映射到第k+1 个粗网格；

3）若达到最粗糙的水平，则使用映射的残差直接求解第k+1 个网格；否则，初始估计为0；

4）通过延长将解vk+1映射到第k个网格，并通过添加vk+1校正解vk；

5）应用平滑，进一步改善第k级网格的vk并返回最终的vk。

该次开发了特定于GPU的GMD 方法。从规则化的电网开始，在整个多重网格层次结构中以几何规则的方式实现多重网格的所有关键组件，从而实现简单的流控制和高度规则的内存访问模式[17-18]。

2.2 混合多重网格迭代

使用该次建立的GMD 方法（如图2 所示）可以有效地解决近似规则的电网问题，而无需进行显式的稀疏矩阵矢量运算。

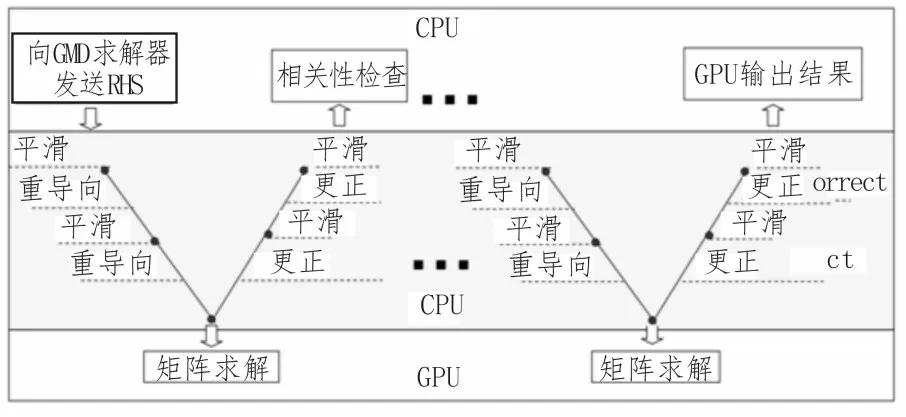
图2 GMD方法

为了保证最终电网解决方案的准确性，其在GPU 与主机之间进一步应用了HMD 迭代，以消除仅解决近似规则网格可能引起的任何错误。用GridO表示真实的数据网，用GridR表示正则化的电网，HMD 迭代涉及以下主要步骤：

1）在CPU 中计算GridO上当前解决方案的残差，并将其残差映射到GridR。

2）在GPU 中使用GMD 解决映射残差下的GridR问题，并将解决方案返回给GridO。

3）在CPU 中 使 用GPU 结果更新GridO解决方案，并应用其他平滑处理。

4）在CPU 中，若解决方法错误足够小，则退出运算；否则，重复上述步骤。

HMD 方法的大量工作通过解决常规网格（即步骤2）在GPU 上完成，仅在主机上执行例如简单的残差计算、平滑步骤等工作。在此方面，通用CPU 在处理原始（不规则）数据的效率更高。

3 实验验证

为证明文中电网工程造价分析系统的性能，使用一组工业电网工程造价基准来比较5 个求解器：基于GPU 加速的分析求解器（GPU GMD）、相同算法基于CPU的实现方案（CPU GMD）、基于GPU 加速的混合求解器（GPU HMD）、相同算法的CPU 实现方案（CPU HMD）以及基于CPU的直接稀疏矩阵求解器CHOLMOD，进行对比实验。所有算法均使用C++和GPU 编程接口CUDA 实现，测试硬件平台是一台Linux 计算机，其CPU 主频为3.0 GHz，带有NIVDIA GeForce 8800 Ultra GPU 图像处理器。

实验结果如表1 所示，当实时残渣达到初始残渣的0.1%（HMD 迭代时取为0.5%）时，将终止GMD解算器。当平均节点电压误差小于0.5 mV 时，将停止HMD 解算器。分析可知，GPU GMD 和GPU HMD较CHOLMOD 快100～350 倍；GPU GMD的速度比CPU GMD 快20 倍；而GPU HMD的速度比CPU HMD快16 倍。此外，使用不同数量的HMD 迭代时，多一次迭代可以显著提高精度。对于大多数基准测试，GPU HMD 产生的平均节点电压误差小于0.5 mV，最大节点电压误差小于5 mV。

表1 五种求解器对比实验

GPU 内存访问时，若算法执行不当，则延迟可能占据主导地位。图3 显示了所有工业基准电路的纯GPU 计算时间与总GPU 运行时间（计算时间+存储器读/写时间）和比率。从图3 可以观察到，纯粹的计算时间只能占总运行时间的一小部分（15%～60%），对SIMT 平台使用更多的本地LBJ 迭代可以更优地减少内存访问延迟。但进行过多局部迭代所产生的收益并不理想，原因在于其无法解决GMD的整体求解问题。因此，应选择合理的局部迭代次数k以在松弛运行时间与全局收敛速度之间进行权衡。

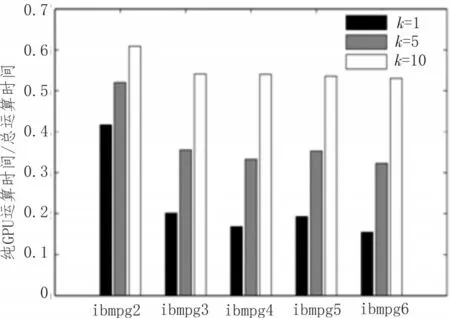
图3 GPU运算时间比

此外，文中在CPU 与GPU 上均运行了500 个平滑步骤。如图4（a）所示，GPU GMD 引擎的CPU 提速达到其18～32 倍速。在GPU 和CPU 上比较了多个周期的SIMT 解决方案运行时间，如图4（b）所示，文中的SIMT 实现了对小网格约10 倍的加速，对大网格约20 倍的加速。

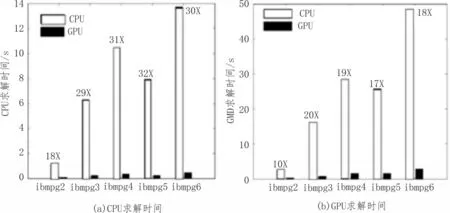
图4 分析引擎提速实验

图5 显示了4 个常见解决方案误差与该方案迭代次数的对比结果。在两次或三次HMD 迭代后，该方案可以迅速地衰减所有4 种平均误差。

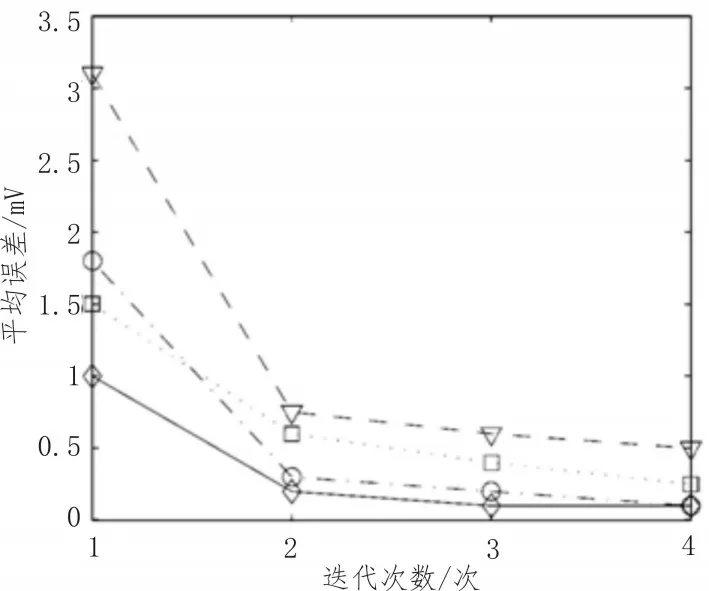
图5 误差衰减实验

使用该次设计的电网工程造价数据分析系统，建筑能源的使用减少了20%：优化前为212 kWh/(m2·a)，优化后为168 kWh/(m2·a)；优化后的已交付能源使用量为216 kWh/(m2·a)。经算法优化后，建筑空间的供暖需求减少了约49%，用于加热生活用水的交付能源需求减少了约40%。

4 结束语

文中通过开发图形处理单元加速引擎，来解决大规模电网系统的造价数据分析。为了在GPU 上获得良好的运算分析效率，将不规则的网格转换为规则的结构，以消除大多数随机存储器访问模式并简化控制流程。为了正确利用大规模并行单指令多线程（SIMT）GPU 体系结构，文中设计了并行几何多网格算法。通过采用新的粗网格结构和块平滑策略，以更加适配SIMT GPU 平台。该算法的鲁棒性通过CPU-GPU 混合多网格迭代方案增强。实验表明，该GPU 引擎可以在直接求解器上实现超过100 倍的运行加速，且较基于CPU的多网格求解器快15 倍，能够实现对电网工程造价数据的准确、快速分析。