基于改进信道补偿的I-vector 说话人识别

罗家诚

（武汉邮电科学研究院，湖北 武汉 430000）

说话人识别是一种生物识别方式，即通过收集到的声音信号进行说话人的身份识别和确认[1]。语音识别技术的发展路径众多，包括说话人识别、自然语言处理、孤立词识别、模糊语义识别、前端语音处理等技术，说话人识别技术因适用性广、应用场景多，在语音识别的众多发展路径中应用更为广泛，同时许多相关技术和研讨也在进行和发展之中。以验证方式划分，说话人识别可以分为文本相关和文本无关两种，其中文本无关[2]的说话人识别技术[3]受语音信道因素的影响，使得说话人识别算法的识别率不理想，限制了应用场景。文中利用因子分析技术(Factor Analysis，FA)[4]将语音特征参数中的高维超向量映射到低维，并通过信道补偿技术，将信道中说话人特征空间与信道空间中的差异进行拟合处理，消除信道因素影响。

身份认证矢量(Identity-vector，I-vector)说话人模型识别过程包含语音信号端点检测[5]、语音信号特征提取[6]和说话人高斯混合模型(Gaussian Mixture Model，GMM)建立3 部分，经前端端点检测后的语音信号通过梅尔频率倒谱系数(Mel Frequency Cepstrum Coefficient，MFCC)提取说话人语音特征参数，使用最大后验概率(Maximum A Posteriori，MAP)自适应算法获得说话人GMM，并建立通用背景模型(Universal Background Model，UBM)[7]。引入信道补偿技术[8]可以消除语音信道差异对说话人识别结果的影响，提高识别率。文中提出一种改进的信道补偿算法，通过改进线性判别算法(Linear Discriminant Analysis，LDA)[9]对I-vector 向量的特征参数进行降维，并利用类内协方差规整[10](Within Class Covariance Normalization，WCCN)对信道进行补偿，提高I-vector 模型系统的识别准确率。

1 I-vector说话人识别技术

1.1 I-vector说话人识别原理

Dehak 和Kenny 发现，使用联合因子分析技术(Joint Factor Analysis，JFA)处理说话人语音信息的方式在现实应用中存在不合理性，因此对JFA 进行了改进，将在JFA 中分开统计的说话人空间和信道空间进行合并，并通过JFA 技术，将语音模型中特征的高维向量映射成低维向量，得到总体变化因子，其对应的矢量模型为[11]：

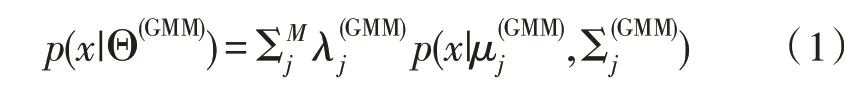
其对应的高斯混合模型参数可表示为：

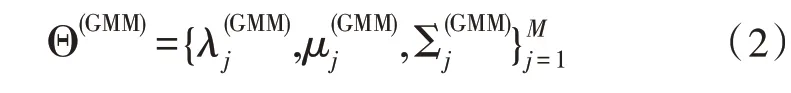
通用背景模型可以作为声纹矢量的度量模型，利用MAP 算法处理通用背景模型，可以将其变成说话人模型:

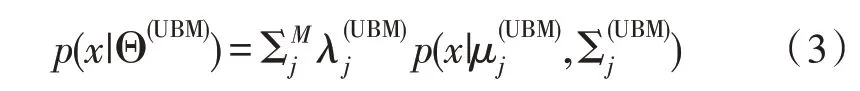
同理，UBM 模型参数表示为：

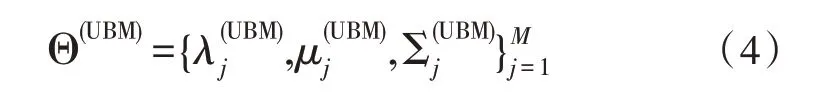
在总体变化空间[12]中，说话人空间和信道空间被映射到同一低维空间，其高斯混合模型的假设如下：

其中各参数的含义如表1 所示。

表1 I-vector模型各参数含义

1.2 I-vector特征提取

说话人语音数据或对应语音片段需要通过MFCC 进行特征提取，得到的特征参数即为对应说话人I-vector 模型特征的参数。利用MFCC 技术处理说话人语音信息前，需要对语音信号进行前端处理，处理完成后的语音信号通过梅尔滤波器组进行参数提取，得到MFCC 特征参数。假设给定一条语音片段如下：

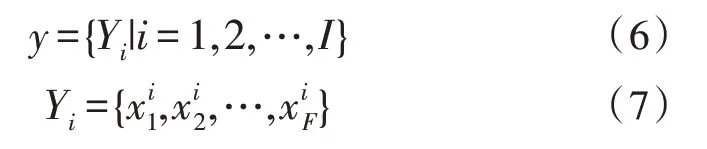
其中，Yi表示一个F维的特征矢量。

通过MFCC 算法提取说话人语音信息特征参数，使用期望最大化(Expectation Maximization，EM)算法进行迭代计算，可以获得说话人UBM 模型。利用MAP 算法调整获得的UBM 模型可以得到GMM 模型。

文中使用I-vector 系统模型提取GMM-UBM 模型中的语音参数，通过理论推导[13]可以得到UBM对应各阶统计量的估计，对应BAUM-WELCH 统计量为：

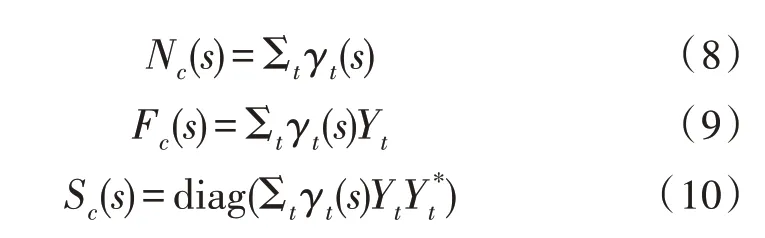
经过BAUM-WELCH 对统计量进行估计后，可以使用EM 算法进行迭代计算，得到总体子空间矩阵T，其步骤及结果表示为：

1）初始化

在T中选择每一组分的初始值，利用BAUMWELCH 方程求得统计量的估计。

2）求E 阶段

求得对应语音片段期望：

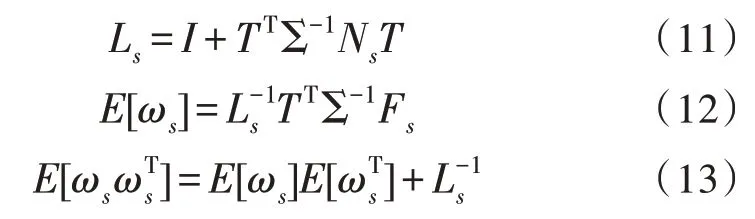
3）求M 阶段

解方程后更新矩阵T：

4）计算完成或继续迭代

若求得对应目标函数收敛，则计算完成，终止EM 步骤；如果未收敛，则继续迭代，直至目标函数收敛。

2 信道补偿

2.1 LDA+WCCN

通过JFA 技术处理语音特征参数[14]，得到的总体变化子空间中包含说话人空间和信道空间两个子空间，使用I-vector 模型进行建模和处理后，总体变化子空间中仍然存在信道信息，影响系统识别准确率。

通过对I-vector 模型处理后的语音信息作信道补偿处理[15],再进行匹配工作，可以解决信道因子对识别准确率的不利影响，通常使用LDA 和WCCN 技术对语音特征参数进行降维并对对应信道空间进行补偿。

LDA[16]利用Fisher 准则，可以加强语音信道空间的类间离散度，由此可以提高不同说话人的区分度，同时减少语音信道空间的类内离散度，聚合同一语音身份的向量空间，提高紧凑性，对应公式如下：

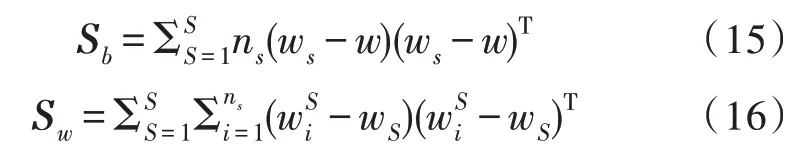
其中，Sb表示信道空间类间离散度矩阵，Sw表示信道空间类内离散度矩阵。

经过LDA 处理后的总体变化子空间无法通过FA 技术获得对应语音信息的类内类间信息，而使用WCCN 进行信道补偿可以补充缺失的类内类间信息。

选取同一数据集中的i个说话人，某个人对应有j句话。使用Wij表示其中第i个人第j条语音的I-vector，则W矩阵表示如下：

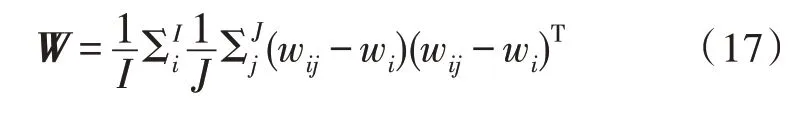
其中，wi用来标识第i个说话人的所有语音均值：

用来映射wij的矩阵B为W-1=BTB的cholesky 分解。映射后wij的表示如下：

2.2 改进LDA+WCCN

通过计算I-vector 向量均值可以计算出类内和类间离散度矩阵，其均值准确性会影响映射矩阵对说话人的建模，因此当建立I-vector 模型时，使用的说话人语音数量较少时，计算得到的I-vector 向量均值准确性降低[17]，导致说话人身份的区分度下降。因此，提出了改进LDA 算法，该算法可以对I-vecotr模型进行信道补偿，并对特征参数进行降维。对经过I-vector 建模后的语音信息进行排序，消除其中的最大、最小样本值，取剩余I-vector的平方均值作为每一类说话人的集中向量，对式(15)、(16)做如下变化：

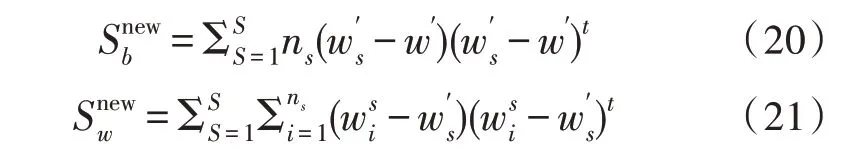
3 实验

3.1 实验设置

实验使用AISHELL 开源语音数据库，从语音库中随机选择20 人，每人10 条语音，其中3 条语音用于数据训练，7 条语音用于数据测试。对于每一个语音信息片段，实验通过MFCC 提取语音中的基本声纹特征，之后进行语音特征提取，并通过语音活动检测消除端点误差。使用训练数据得到声纹信息的通用背景模型，将测试数据的声纹特征与通用背景模型通过I-vector 模型计算后得到初始I-vector，将得到的总体变化子空间因子I-vector 进行信道补偿处理，并通过分类器进行打分判决处理，得到系统识别准确率[18-19]。

3.2 实验结果及分析

文中使用两组对比实验，采用识别准确率对实验结果进行度量，使用MFCC 技术提取测试集及训练集语音信号的特征参数。实验一以12 阶MFCC 作为基准参数，与其一阶、二阶差分组成24 维和36 维特征参数，验证加入差分系数的信道补偿对识别准确率的影响，其中GMM 混合数为512；实验二使用LDA+WCCN 作为基准参数，将I-LDA+WCCN 与其进行比较，测试两种方式对最终识别准确率的影响，其对应的GMM 混合数为512。

表2 为实验一的识别结果。从实验结果可以看出，I-vector 模型使用一阶和二阶差分MFCC 提取特征参数后，系统识别准确率有提升。通过I-LDA+WCCN 技术处理后，I-vector 模型算法识别率得到提高。对比一阶MFCC，引入信道补偿算法后系统识别准确率有提高；但在二阶MFCC 情况下，算法识别准确率出现下降趋势，表明引入二阶MFCC 后特征参数增加，引起GMM 模型特征参数向量维度增加，同时说话人语音身份信息也因引入二阶MFCC出现部分丢失，系统特征参数的区分度降低，对应扰度增加，增加信道补偿算法无法弥补二阶MFCC引起的干扰，导致识别准确率下降，但是相对于未引入信道补偿算法，I-vector 模型的识别准确率均有所提高。

表2 引入信道补偿系统识别准确率

如图1 所示，分析获得的实验结果信息可知，特征参数维度的增加在进行信道补偿前对算法识别准确率的影响不大，在使用信道补偿算法后，模型识别准确率相比未使用信道补偿有较大提高。

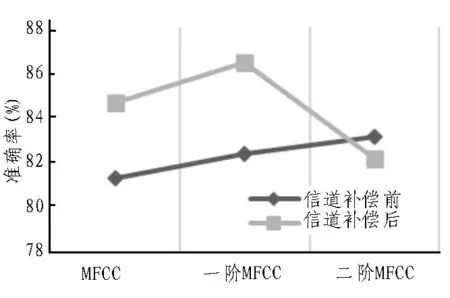
图1 信道补偿对比图

实验二将LDA+WCCN 和I-LDA+WCCN 分别应用于I-vector 向量并通过分类器进行判决，测试其对语音信道间干扰的抑制效果及对特征参数降维的性能。说话人语音数量的样本数取5～10 段，对每种情况进行5 次测试求取对应识别准确率平均值，如表3和图2 所示。

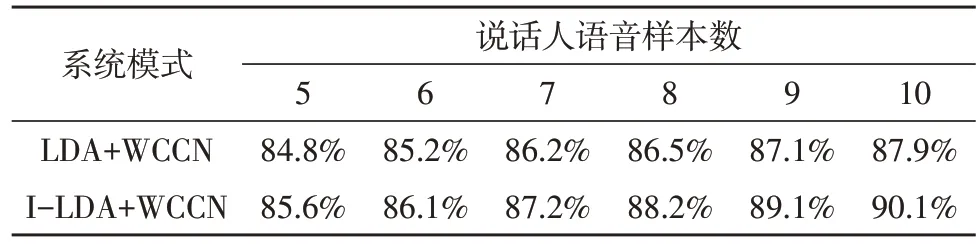
表3 信道补偿算法识别率比较

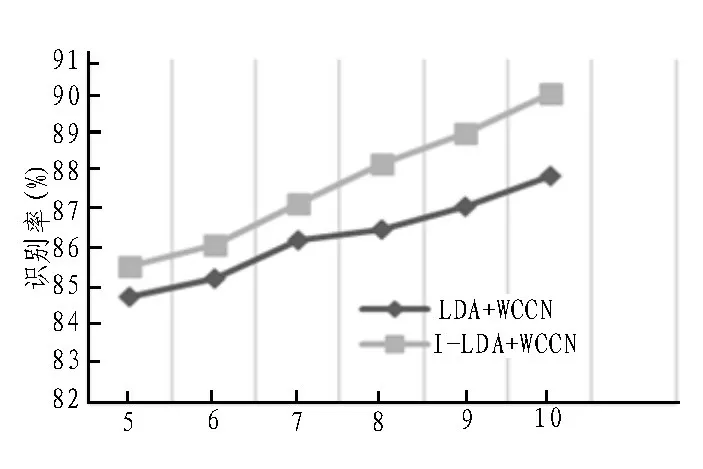
图2 识别率对比

通过表3 可知，说话人语音样本数量增加时，两种模式下系统识别准确率均有提高，表明随着样本数量增加，其中包含的说话人信息增加，有利于提高系统的区分性；样本数较少时，I-LDA 方法与LDA 方法相比优势不大，区分性不明显，当样本数增加时，I-LDA 方法可以达到更好的效果，对系统识别准确率提升明显。

从以上实验可知，I-vector 模型进行信道补偿后识别准确率得到提升，可以更好地进行说话人识别，使用改进I-LDA 算法，可有效提高系统区分度及识别准确率。

综上所述，使用I-LDA+WCCN 处理I-vector 模型，能够有效消除信道差异，可以使I-vector 模型能更好地表达说话人语音身份特征，能够提高系统识别准确率。

4 结束语

通过改进LDA 信道补偿技术，对初始I-vector 模型类内和类间信息进行补偿，降低了信道空间对说话人识别准确率的影响，提高系统区分度，相比于传统I-vector 模型具有更好的识别准确率。同时，与LDA+WCCN 基准进行对比，在样本数多的情况下，改进的方法具有更好的区分性能。