基于最优几何匹配的时间连贯3D 动画重建

王建华，冉煜琨

（成都理工大学工程技术学院，四川乐山 614000）

3D 动画重建[1]在现代多媒体、测绘等众多领域具有重要的应用。很多方法利用多视角RGB 数据重建3D 动画，通过形状匹配和形变等技术捕捉时间连贯的动画。其中，时间连贯性是所有动画重要且必需的属性，很多后处理任务也要求时间连贯性，例如视频编辑压缩、场景分析等[2]。对于使用RGB 数据的系统，3D 重建要求两个或更多的相机来进行深度重建。因此，重建的质量也取决于底层的特征点提取和图像配准算法等。

过去十多年中，已有研究者对该问题进行了一些研究。如Yan 等[3]利用大量迭代计算对多视角视频采集装置进行扩展，捕捉不同静态和动态光照条件下的物体。Kawami 等[4]对自由视点视频研究进行了扩展，并使用多个高分辨率彩色摄像机对点光源进行校准，以采集行人的形状、运动、表观以及表面反射特性。在动态表面反射估计的基础上，可以在不同的光照条件下对重建的3D 动画进行渲染。这些方法[3-4]的主要缺点是依赖于色彩数据的研究，必须利用相机之间的对应关系来重建深度信息。

随着低成本深度传感器特别是微软Kinect[5]的面世，结合深度传感器以采集静态和动态3D 内容成为了研究热点。使用Kinect的一大好处是Kinect的帧率可以达到30 fps，满足实时处理要求，同时还提供色彩和深度数据。如文献[6]提出一种有效从深度相机获取的低质量动态数据中直接分析出刚性关节式物体运动特征的RANSAC 方法。与传统的运动特征重建方法不同，该方法完全跳过了重建物体本身的几何信息，提取物体每个关节的运动类型、运动参数等信息。文献[7]使用来自Kinect的深度数据进行3D 形态重建。该方法将低分辨率图像轮廓与粗粒度数据相结合，以估计参数模型。类似地，文献[8]提出一种带有深度约束和局部近邻约束的基于RGB-D的室内场景实时三维重建方法，该方法首先利用RGB-D 相机采集的RGB 图像做哈里斯角点检测，利用特征点集合的深度信息和局部近邻特征点信息作为约束，在图优化方法的基础上生成三维点云，实现室内场景的三维重建。但没有从捕捉到的深度数据及色彩数据中提取出时间连贯性信息。文献[9]在姿态估计框架中采用单个深度相机来跟踪整个身体的运动情况，利用单个深度传感器进行姿态估计。

文中提出了从RGB-D 视频数据中生成时间连贯的3D 动画重建方法。在数据采集后，从映射到深度数据的RGB 数据中提取光学特征点，以得到两个帧之间的初始稀疏3D 对应关系。在此基础上，利用迭代几何匹配程序进行特征点细化，以得到3D 点的无偏匹配。与以往相关方法相比，所提方法具有以下优势：1）使用隐式三维数据，利用动态对齐进行跟踪，而以往很多方法则依赖于RGB 数据的三维重建，且不依赖于动态场景对象的底层表征；2）提出的几何匹配方法纠正了从RGB 到深度映射过程中产生的误差，以往方法则不能直接处理该问题。实验结果也验证了所提方法的有效性。

1 数据采集和校准

Kinect 以30 fps、每帧640×480 像素同时提供RGB 和深度数据。文中的RGB-D 视频采集系统包含多个Kinect。在使用两个Kinect的情况下，两者之间的放置角度约为90°。当使用超过两个Kinect 进行数据采集时，必须解决两个问题：相机之间的同步化和干扰问题。对于同步化采集，文中遵循了文献[10]的技术原理。

Kinect的新SDK 直接提供了颜色数据和深度数据之间的映射，以及深度数据到现实世界距离的映射。由此可以利用每个3D 位置的RGB 数值映射，从采集的RGB-D 视频[11]中以3D 点云的形式对每帧进行重采样。来自一个或多个相机的RGB 数值的3D点云序列是文中方法后续所有步骤的主要数据容器。实践时，使用点云库[12（]PCL）以高效保存3D 点云，并利用点云库在统一的全局坐标体系中记录来自不同相机的点云。由此，对于每个视频帧，将来自多个相机的点云合并为统一的点云。此外，文中实施了简单的基于深度的分割以进行背景减除。演示过程如图1 所示，其中，采集装置从Kinect 捕捉到RGB 图像和深度帧、来自每个相机的3D 点云以及包含或不包含RGB 映射的统一化3D 点云。其中，图1(a)的上图和下图分别是来自两个相机的输入RGB 和深度图像。图1(b)是在3D 点云中对每个相机的RGB-D 数据进行的单独重采样。图1(c)的上图将点云合并到统一全局坐标系中，图1(c)的下图包含了RGB 映射的结果。

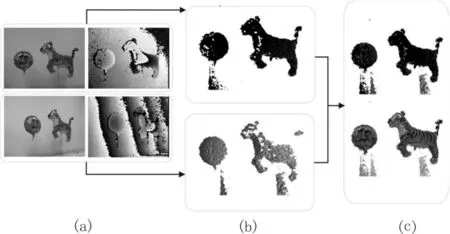
图1 演示过程图例

2 3D动画重建方法

文中系统的输入为3D 点云序列，其中包含来自一个或多个相机的RGB 映射。每帧的3D 点云彼此独立，且每帧中的3D 点云数量是不同的。假设将一个3D 点云表示为C=(V,T)，其中(V,T)表示所有3D点的集合以及这些3D 点在点云中的RGB 映射。由此，对于(V,T)∈C，将每个3D 位置p与一个3D 点(x,y,z)相关联，并将其纹理坐标(u,v)与每个纹元（图像中的2D 位置）q∈T相关联。利用T将从深度数据中得到的所有3D 位置V映射到对应的RGB 数值。因为文中分析对象是包含N个时间帧的视频序列，所以将点云序列表示为时间t的函数。由此得到C(t)=(V(t),T(t))，其中t=0,…,N-1。

文中算法旨在通过将C(0)迭代地映射到序列中的每个C(t)，在整个动画序列上对C(0)进行跟踪。也就是说，首先通过从C(0)到C(1)的映射得到与C(1)对齐的C0(1)，即V(0)∈C(0)。由此，C0(t)指的是在算法的t次迭代后与C(t)相对齐的C(0)，其中t=0,...,N-1。在这方面，文中公式与其他任何跟踪系统均没有显著差异。文中将描述针对任何给定的t得到C0(t)的算法。从输入阶段到输出的流程如图2 所示，其描述了从输入阶段到时间连贯3D 重建输出的系统流程。

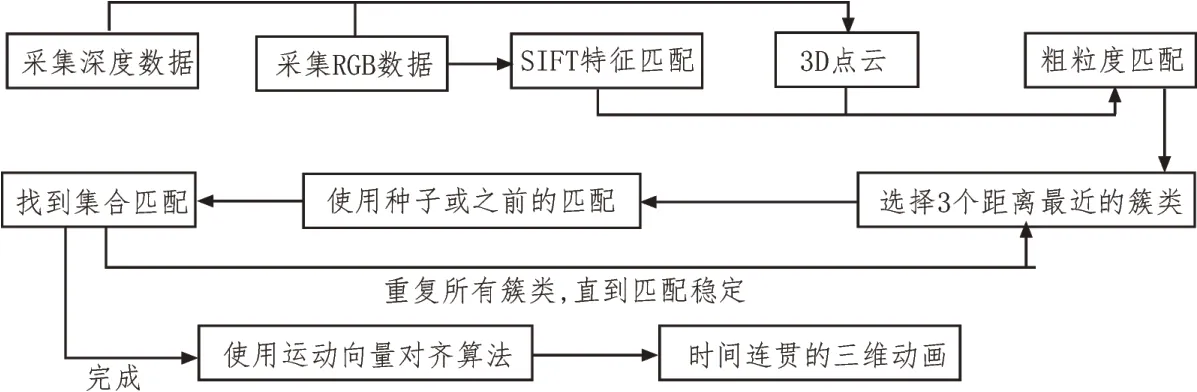
图2 从输入阶段到输出的流程

2.1 特征点估计

对于每个输入RGB 帧Ic(t)，首先，针对所有时间步t和相机c，提取2D 尺度不变特征转换[13（]SIFT）的位置。对于记录的所有RGB-D 视频序列，针对每个输入图像得到约200～300 个特征。使用SIFT 特征在很多方面具有优势，包括准确度、稳定性、旋转不变性和尺度不变性等。每个SIFT 特征在纹理空间中均有一个位置q(t)=(u,v,t)，利用(V(t),T(t))∈C(t)可以将每个SIFT 特征映射到相应的p(t)∈V(t)。文中将时间t处与SIFT 特征点相关联的所有3D 点的集合表示为光学特征点L(t)。

然后利用简单欧氏距离度量D，找到相应SIFT特征之间的匹配，以建立L(t)与L(t+1)之间的映射。在很多基于SIFT的匹配算法中，这是一个非常简单的步骤，若最近特征和次近特征之间的比例低于某个特定阈值，则建立一个匹配。该度量还有助于去除大部分假阳性样本。

然而，从RGB 至深度数据的映射是“一对多”而非“一对一”的，由此使得单个q(t)被分配至3D 空间中距离较近的多个p(t)。因此，存在多个与相同的SIFT 特征相关联的特定点l(t)∈L(t)。若利用从L(t)到L(t+1)的特征点匹配对C(t)与C(t+1)进行匹配，那么应该首先解决这个不确定性问题，且t处的一个SIFT特征应该仅与一个p(t)相关联。所提方法通过使用一个几何匹配算法选择最可靠的特征点，从而消除这种不确定性。

2.2 最优几何匹配算法

为解决一个SIFT 特征与多个光学特征点匹配相关联的不确定性问题，文中提出了一个迭代算法，基于几何匹配选择最优匹配。给定光学特征点L(t)，则定义一组簇类ls(t)∈L(t)，其中ls(t)中所有的p(t)均与一个SIFT 特征相关联，s=0,...,NoC－1，其中，NoC表示分簇数量。使用前文介绍的距离度量D，将分簇ls(t)匹配到ls(t+1)。因此，一个SIFT 特征与p(t)和p(t+1)的“一对多”映射，成了ls(t)与ls(t+1)之间的“多对多”映射。为了找到ls(t)与ls(t+1)之间的最可靠的“一对一”映射，文中使用以下算法：

首先从所有的p(t)∈ls(t)中随机选择一个ps(t)，并从所有的p(t+1)∈ls(t+1)中随机选择其匹配的ps(t+1)。选择分簇之间的随机映射并不能得到理想的结果，解决了“多对多”的不确定性，并给出了作为算法起始点的L(t)与L(t+1)之间的初始对应关系。假设该初始映射为M(t)。给定初始对应关系M(t)，则可以通过执行以下步骤，找到ls(t)与ls(t+1)之间的最佳匹配：

步骤1：对于给定的簇类ls(t)，从M(t)中选择3 个三维空间特征点位置Lp0(t)、Lp1(t)和Lp2(t)，以使得Lp0(t)=ps(t)，已 知Lp0(t)、Lp1(t)和Lp2(t)是非共线的，Lp1(t)和Lp2(t)被选择为与Lp0(t)有着最近欧氏距离的特征点位置。

步骤2：对于给定的簇类ls(t+1)，按照与步骤1 描述的相同方式，针对t+1，从M(t)中选择3 个三维空间特征点位置Lp0(t+1)、Lp1(t+1)和Lp2(t+1)。

步骤3：使用位置Lp0(t)、Lp1(t)和Lp2(t)定义具有法线n(t)的平面P(t)。

步骤4：使用位置Lp0(t+1)、Lp1(t+1)和Lp2(t+1)定义具有法线n(t+1)的平面P(t+1)。

步骤5：将所有的P(t)∈ls(t)投射到平面P(t)，并得到其在P(t)上的参数坐标(a,b,t)。从Lp0(t)、Lp1(t)和Lp2(t)中随机选出平面的根点。

步骤6：将所有的P(t+1)∈ls(t+1)投射到平面P(t+1)，并得到其在P(t)上的参数坐标(a,b,t+1)。从Lp0(t+1)、Lp1(t+1)和Lp2(t+1)中随机选出平面的根点。

步骤7：将ls(t)和ls(t+1)之间的一个新匹配定义为两个点ps(t)和ps(t+1)之间的匹配，这两个点的参数坐标(a,b,t)和(a,b,t+1)距离最小。

步骤8：更新M(t)中的映射ps(t)和ps(t+1)。

步骤9：重复处理所有簇类，直至匹配稳定。

几何匹配算法的结果为L(t)和L(t+1)之间的一对一对应关系M(t)，由此给出了C(t)和C(t+1)的直接对应关系。文中算法受文献[14]研究的启发，利用基于几何的映射算法得到了两个帧的正确稀疏匹配，该映射算法使用基于颜色的匹配作为起始点。文中利用簇类中两个点的随机匹配、簇类的质心匹配以及几何匹配对时间连贯性进行估计，从而对提出的几何匹配算法进行验证。

虽然现在已经得到了C(t)和C(t+1)之间的基于特征点的对应关系，但依然不足以对齐两个点云，因为仅得到了200～300 个特征点匹配，而点云中点的数量超过60 000 个。

2.3 运动向量对齐

为了对齐C(t)和C(t+1)，需要找到V(t)∈C(t)的映射，而基于特征点的对应关系给出了稀疏匹配M(t)。为了针对与M(t)中的任何特征点均无关联的所有p(t)∈V(t)建立映射，文中进行的算法步骤如下：

步骤1：找到与p(t)的欧氏距离最小的N个特征点位置Ln(t)，其中n=0,…,N-1。

步骤2：利用M(t)找到Ln(t)到t+1的映射Ln(t+1)。

步骤3：找到运动向量Vn(t)，满足Vn(t)=Ln(t+1)-Ln(t)。

步骤4：计算所有Vn(t)之和并除以N，得到p(t)的平均运动向量Vp(t)。

步骤5：通过p(t+1)=p(t)+Vn(t)，得到p(t)的匹配p(t+1)，即匹配点位于Ln(t+1)到Ln(t)平均运动的相同距离处。

特征点可视化和对齐算法如图3 所示。其中，图3(a)为缩小的点云，图3(b)为时间步t处放大的点云。根据5 个最近特征点计算出运动向量。使用这些运动向量计算t+1 处的匹配点，如图3(c)所示。其中，在给定动态对象任意运动的情况下，形变在很大程度上是等距的，由此可以证明文中的全局对齐算法是合理的。显然，对于极端的非等距形变，文中算法并不适用。另一方面，文中在大量数据集上对算法进行了验证，结果表明该算法能够以很好的准确度提取时间连贯性。即使噪声造成深度数据在一些区域存在空洞，或深度传感器受限且无法推导出该区域运动信息的极端情况下，文中方法依然能够利用最近特征点进行运动跟踪。

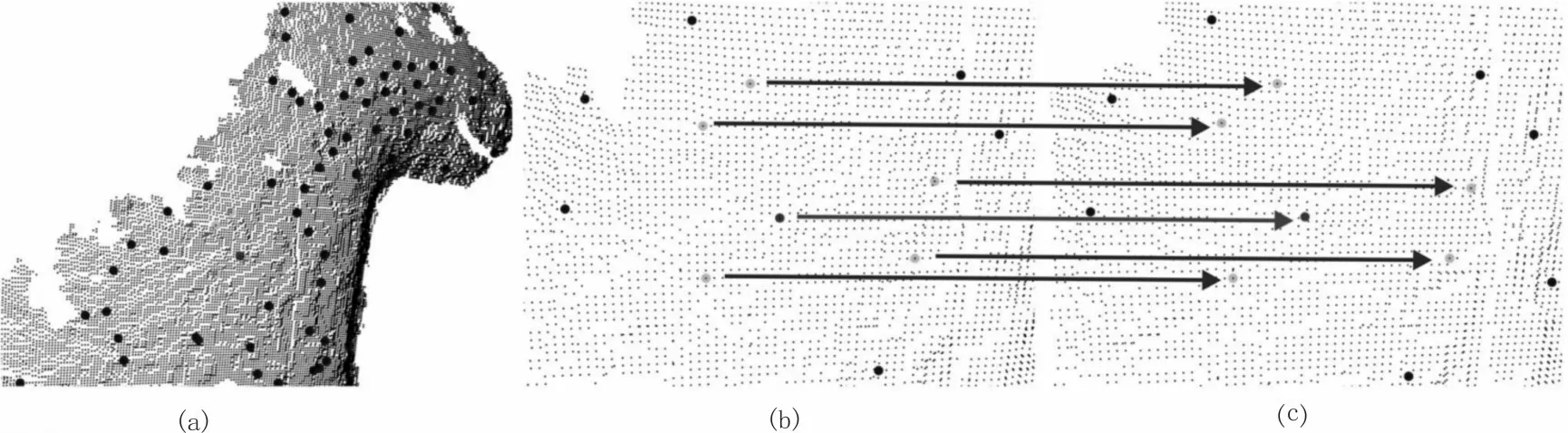
图3 特征点可视化和对齐算法的演示

给定C(t)和C(t+1)之间建立的对齐，文中跟踪算法从t=0 开始，将C(0)映射到C(1)得到C0(1)，即使用L(0)和L(1)之间的特征点匹配M(0)将C(0)与C0(1)相对齐。然后，将C0(1)与C(2)对齐，运用L(1)和L(2)之间的特征点匹配M(1)得到C0(2)。由此，在算法后续的每个步骤中，将跟踪点云C0(t)与C(t+1)对齐，运用L(t)和L(t+1)之间的特征点匹配M(t)得到C0(t+1)。因此，文中方法在整个序列上跟踪C(0)，得到具有时间连贯性的3D 动画。

3 实验结果与验证

3.1 数据集

文中在3 个数据集上应用了所提3D 动画重建方法。其中两个数据集来自运用两个Kinect的RGB-D 视频采集系统。另一个数据集包含通过8 个RGB 相机采集到的行人，并从重建的视觉外壳中提取出点云。所有序列长度均超过100 帧。对于前两个数据集，两个连续帧之间的特征点匹配平均为300 个，而对于第三个数据集，每个帧的特征点匹配仅有150 个。前两个序列每个相机中点的数量平均为60 000，而第三个序列则稀疏得多。

文中方法能够从带噪RGB-D 数据中可靠地重建出时间连贯的3D 动画。即使存在较大空间和时间噪声的情况下，所提方法依然能够从非连贯数据中提取出时间连贯性，特别是当RGB-D的视频流中深度数据缺失造成点云中存在空洞的情况下。即使最后一个序列并非通过RGB-D 采集框架得到，只要该数据集为包含相应RGB 数据映射的动态点云格式，就可使用该数据证明所提算法能够在多种数据集上工作。

3.2 主要评价参数

为了进行定量分析，文中开发了一个畸变的度量，以检查不同初始条件下3D 重建动画的质量。假定动态目标经过了较小的形变，通过比较每帧较小点集之间的距离来测量畸变。为此，对于起始帧，对C(0)上均匀分布的200 个点进行采样，并将每个点之间的距离向量保存在列表Ei(0)中，其中i=0,…,||E||-1，||E||为Ei(0)中的总向量数。在跟踪之后，针对每个跟踪帧C0(t)计算相同的距离向量Ei(t)，其中t=1,…,N-1。将每帧在每个时间步t处的误差度量Ei(t)定义为：

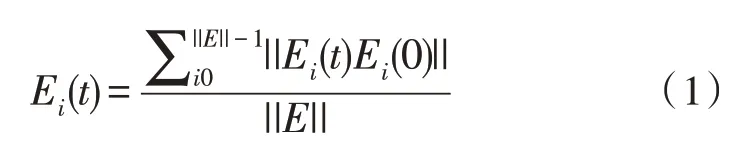
而整个序列的平均误差度量E则定义为：

利用平均误差度量E来寻找N的最优数值，以实现低畸变和高跟踪质量。并且使用该度量验证文中提出的几何特征点映射算法。

3.3 定量分析

实验中的定量分析主要测试几何特征点映射步骤是否能够提高跟踪性能、最近特征点数量N对跟踪结果的影响，以及N的优良值。

对齐算法寻找N个最近特征，从而为每个p(t)构建向量场。N的数值很大程度上取决于运动类型和目标形状。例如，若通过全局变换对目标作动画处理，那么增加N的数值并不会引起显著误差，会使运动正规化，从而减少每个匹配的平均误差。另一方面，若在一些全局运动之外，目标的个体区域也经过了局部运动，例如，人体的一部分做了独立移动，那么增加N的数值并超过特定阈值将导致不正确的动画。对于图1的“老虎气球”序列，由于局部运动较少，随着数值N的增加，整个序列的平均误差逐渐变小。

对于包含“老虎气球”的序列，不同数值N下的平均误差如表1 所示。表1 中分别给出了使用簇类中两点的随机匹配、簇类的质心匹配以及几何匹配时的误差情况。从中可以观看到，当使用10 个最近特征点时，平均误差约为2.55%，而使用20 个最近特征点时，平均误差约为1.90%。表明随着数值N的增加，误差的下降并不是线性的。虽然较大的N值能够降低总体误差，但也会造成运动的正规化。在所有案例中，几何匹配得到的结果误差最小，特别是在数值N较小的情况下。由此，对于气球序列视频，文中取N=10 并生成了所有结果。

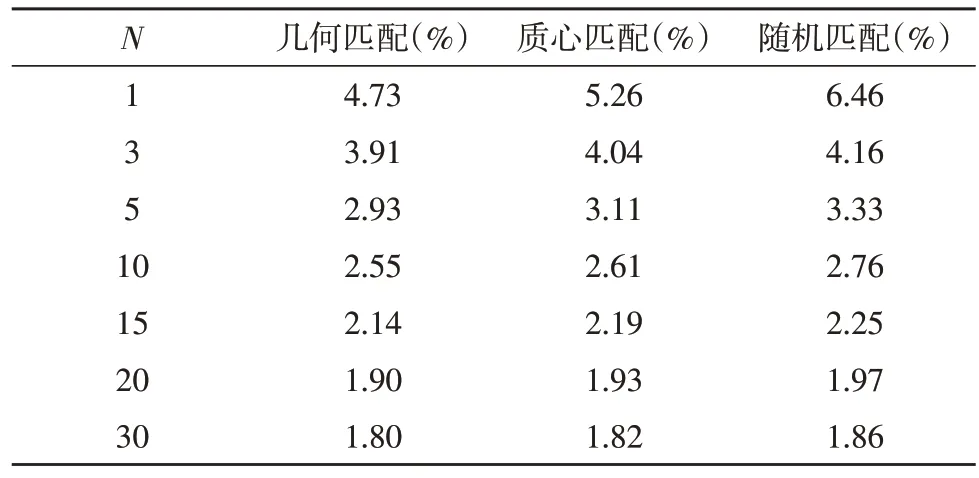
表1 平均误差的比较情况

为了对几何特征点映射进行验证，使用了随机匹配、质心匹配和几何匹配时的每帧平均误差和整个序列平均误差。当N=5 时，使用随机匹配、质心匹配和几何匹配时，包含一个老虎气球的RGB-D 序列的平均误差比较如图4 所示。可以看出，文中几何匹配的误差明显更小，这说明所提匹配方法很好地解决了SIFT 特征与多个光学特征点匹配相关联的不确定性问题。

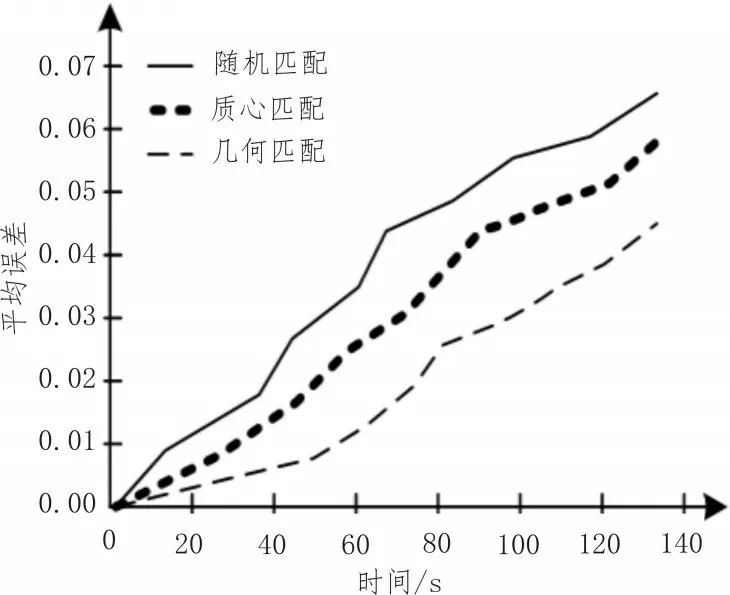
图4 不同匹配的平均误差比较

对于包含两个“老虎气球”的多目标序列，文中使用两个度量，即多目标跟踪精度（MOTP）以及多目标跟踪准确度[15（]MOTA），以评价点云的时间连贯性。平均而言，当N=5 时，MOTP小于7 mm，MOTP则大于95%。因此，所提方法在准确度和精度两方面均取得了优秀的结果。另外，对于非连贯点云的轮廓与连贯点云轮廓重叠[16]的差异。所提方法得到的平均误差均低于2%。这表明该重建方法能够实现对动态序列的可靠跟踪[17-19]。

为了对所提方法与文献[7,9]方法进行比较，使用公开的capoeira 序列[7]。其平均误差情况如表2 所示。在使用质心匹配和随机匹配时，误差大致相当；而使用文中的几何匹配算法能够将误差平均降低0.5%，这与文中在采集的RGB-D 序列上的测试结果基本一致。

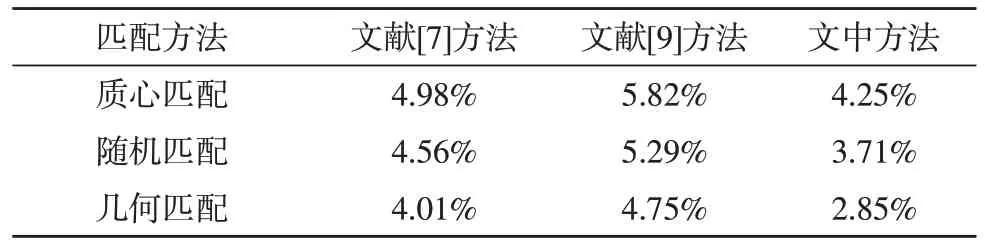
表2 各方法的平均误差情况

各方法重建的帧图像如图5 所示，可以看到，文中方法的3D 动画在不同帧中保持一致，与之相近的是文献[7]方法，该方法也取得了不错的视觉效果，而文献[9]的数据发生了显著的变化，尤其是头部数据，存在的缺失比较多。为了从另一个方面进行比较，显示的三维点云情况如图6 所示，可以看出文献[7,9]方法的点云发生了轻微的变化，其中文献[9]方法给出的点云变化最大，文献[9]采用单个深度相机，有时会产生明显的数据丢失。

图5 各方法重建的帧图像

图6 三维点云比较

此外，所提方法具有计算方面的高效性，平均而言，可以每分钟25 帧的速率进行时间连贯动画的重建。在配置了酷睿双核i5 处理器（RAM 8GB @2.6 GHz）系统时，处理一个100 帧的序列耗时约5 min，其结果如表3 所示。可以看出，所提方法比文献[9]的处理速度快25%，与文献[7]的处理速度大致相当。

表3 各方法处理100帧的耗时情况

4 结论

文中提出了从单视角或多视角RGB-D 视频数据中重建时间连贯的3D 动画方法，使用了无偏特征点采样和几何映射。提出的几何映射算法用于推导3D 点云中所有点到下一帧的全局映射。实验评价在多个Kinect 记录的数据下进行，实验结果验证了所提方法的有效性，在误差和运行时间方面的性能表现优秀。所提方法可以用于视频剪辑、压缩或场景分析等。

所提方法也存在一些局限。如方法中的所有步骤都需要依赖欧氏距离进行度量，一定程度上是由硬件约束导致的。未来，将从这方面进行完善和改进。