一种基于极限学习机和皮尔逊相关系数的光伏阵列故障快速诊断方法

陈世群 高 伟 陈孝琪 涂彦昭 杨 艳

一种基于极限学习机和皮尔逊相关系数的光伏阵列故障快速诊断方法

陈世群1高 伟2陈孝琪2涂彦昭2杨 艳3

（1. 国网福建省电力有限公司福州市长乐区供电公司，福州 350202； 2. 福州大学电气工程与自动化学院，福州 350108； 3. 淮阴工学院自动化学院，江苏 淮安 223003）

光伏阵列故障会造成能量损失，甚至引发供电中断或火灾事故。因此，对故障的快速识别至关重要。本文提出一种光伏阵列故障快速诊断方法，用于快速感知故障及故障发生的时刻。通过分析光伏阵列常见故障的信号变化规律，提出利用正常运行时的功率波形训练一个极限学习机预测模型，用于预测短时功率的变化；接着计算实测波形和预测波形的皮尔逊相关系数；若光伏阵列发生故障，相关系数将低于一定的阈值，从而识别故障的发生。实测实验验证了所提方法具有很强的故障辨识能力，准确率达到99.37%。所提方法的故障辨识时间仅为4.355ms，亦可作为光伏阵列故障录波的启动方法使用。

光伏阵列；故障录波；极限学习机（ELM）；皮尔逊相关系数

0 引言

近年来传统化石燃料逐渐枯竭，且化石燃料所引起的环境污染问题日益严重，人们对可再生清洁能源的需求不断提高。太阳能发电在不产生有害物质的前提下，将太阳能直接转换为电能，得到各国的青睐和广泛应用。在过去的十年里，光伏装机容量快速增加。根据国家能源局官网发布的《国家能源局2021年一季度网上新闻发布会文字实录》[1]，截至2020年底，我国累计光伏并网装机容量已经达到253GW，位列世界第一；光伏全年发电量达到2 605亿kW·h，同比增长16.1%。

光伏阵列安装在室外环境，持续暴露在恶劣的环境条件（阳光、降雨等）下会诱发各种故障，导致发电效率降低。当故障严重时甚至会损坏设备，造成火灾等严重安全事故[2]。因此，对光伏阵列的故障识别和故障诊断至关重要。光伏阵列的故障诊断方法可分为离网诊断和并网诊断两种。离网诊断方法是在光伏系统退出运行的情况下，通过专用设备，执行电流-电压（-）扫描操作，获得当前状态的-曲线。接着针对该曲线，推导光伏阵列的内、外特征参数。根据故障前后内、外特征参数的变化规律，识别光伏阵列的故障类型。文献[3]提出一种通过观察和评估电压、电流的变化来诊断光伏故障的新方法。用开路电压、短路电流和最大功率点的电压、电流来定义电压、电流指标，并根据故障特征的变化确定阈值。通过对实时采集的指标值和阈值的比较，判断系统是否存在故障。由于受电站规模、组件参数的影响，通过阈值判断故障状态的方式，泛化性较弱，在组件性能老化时，阈值需重新确定。文献[4]以-曲线中mpp、mpp、sc、oc等4个特征参数作为辨识特征量，通过大量的标签样本训练BP神经网络，从而建立一个能够识别短路、开路、老化和遮阴的诊断模型。文献[5]首先利用Lambert W函数重新建立光伏阵列的-关系，然后提出使用混沌粒子群算法搜索光伏阵列的模型参数，估计出5个内部参数。将正常和异常状态的参数进行比较实现故障辨识。参数估计法往往只能求得局部最优值，而不是全局最优值。两个结果相似的解析解差异可能很大。因此，以最优值代替真实值进行诊断容易导致误判。离网诊断方法的最大缺陷是难以实现实时的故障诊断，导致故障无法在第一时间被检测到，并且在执行-曲线扫描时，需要断开网络，造成人为的能量损失。

并网诊断方法是在光伏系统运行时，利用电压、电流波形在故障发生前后的变化规律识别故障类型。常用于解决多串列系统的线间故障、动态遮阴及电弧故障诊断问题[6]。线间故障又称为失配故障，因线间故障存在故障电流回流的现象，故常采用瞬时波形分解及时频变换来提取故障特征、辨识故障类型。而失配比例、接地电阻的大小及阻塞二极管的使用，都会限制故障电流的产生和变化，给故障辨识带来很大困难。文献[7]从理论上解释了线间故障及其演化过程，通过仿真和实验研究，证明了在低失配比、高阻抗、低辐照度或昼夜变化等条件下，故障串的回流电流不足以让过电流保护装置动作，给系统的安全运行带来很大隐患。为此，文献[8]利用光伏阵列输出特征中右侧功率峰值（right power peak, RPP）的惟一性来检测线-线、线- 地故障，使用全局的扰动观测的最大功率点跟踪（maximum power point tracking, MPPT）算法来追踪RPP。实验结果表明，该方法可以有效检测出故障，而与失配级别、系统类型和系统额定值无关。在低辐照度和局部遮阴下，同样有效。文献[9]将功率数据进行经验模态分解，将分解后得到的固有模态函数（intrinsic mode function, IMF）分量、分解余项和相关因素（太阳辐射强度、湿度、温度）作为BP神经网络的输入变量，建立一个能够实现短时功率预测的模型。然而，传感器存在安装角度偏差，阵列积灰或老化都会影响该方法的准确性。文献[10]利用提取的低分辨率功率和照度损失比计算阵列损失，寻找多串列光伏系统中，失配、局部遮阴和正常状态在上述特征量范围内的幅值差异，进行故障探测。并网故障诊断法的优点是无需停机即可辨识故障，避免了人为的功率损失。但若故障发生在逆变器停机期间，由于无法提取波形变化的数据，这类方法就会失效。因此，需要将并网和离网故障诊断方法相结合，从而实现光伏系统故障的快速、准确识别。

目前，绝大部分的研究主要关注使用何种算法对已获得的数据进行准确诊断。这些数据大多是通过仿真和实验获得，并通过人工选取的方式得到理想时间窗的信息。在实际应用中，首先需要能辨识故障，自动发现故障发生的时刻，记录故障发生前后的波形，再利用前述诊断方法辨识故障类型。因此，故障自动录波是故障辨识的前提，为故障辨识提供数据支撑。鉴于这方面的研究工作甚少，本文提出一种基于极限学习机（extreme learning machine, ELM）和序列相关系数的光伏系统故障快速诊断方法，通过比较发电功率的预测波形和实际波形的相关系数变化，实现光伏系统的故障诊断和对故障时刻的甄别。

1 故障波形特征分析

并网故障检测可以辨识开路、遮阴、线间等故障类型。在不同的故障类型下，电压、电流、功率的波形在故障瞬间均会产生特异性波动。各状态下的时序电压、电流如图1所示。正常状态下，电压、电流、功率波形均保持规律性变化，如图1（a）所示。

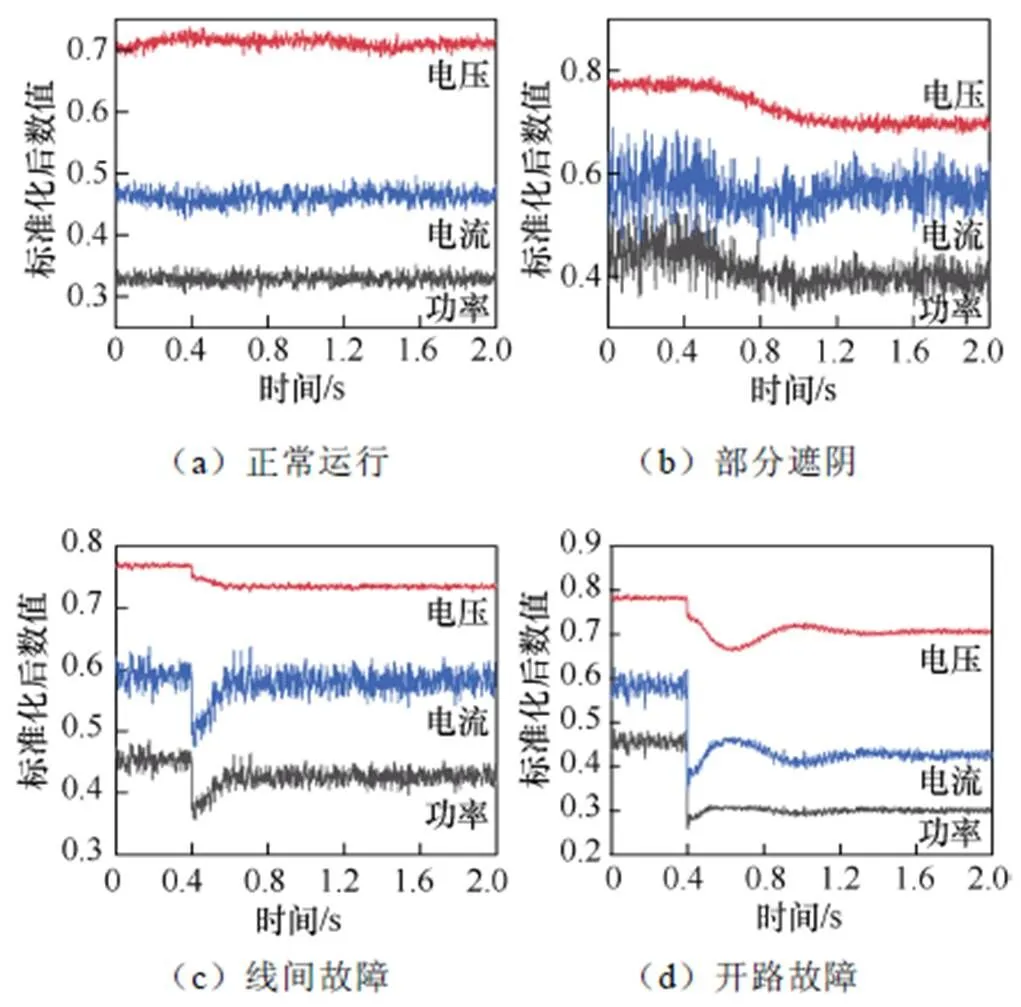
图1 各状态下的时序电压、电流

部分遮阴指光伏阵列的某些模组被云层、树木、建筑物等物体遮挡，导致阵列输出功率出现受损的情况。遮阴故障发生时，被遮阴模组的辐照度会逐渐减小，所以阵列的总输出电流开始下降。当被遮阴模组的辐照度减小到一定程度时，对应的旁路二极管就会因电压差而被激活。此时被遮阴模组短路，阵列输出电流出现回升，而阵列电压因为被遮阴模组短路而变小，这个过程的时序波形如图1（b）所示。

线间故障指在光伏阵列中，两个不同电位点发生连接，导致部分光伏模组被短路，进而导致阵列的输出功率受到损失[11]。线间故障可以发生在同一光伏串内，也可发生在相邻的两个光伏串之间。被短路的模组越多，则失配比越大，线间故障越严重。这个过程的时序波形如图1（c）所示。由于故障电流容易受到光照辐射度和MPPT的影响，线间故障在光伏阵列中难以检测，特别是低失配比的线间故障，波形的变化非常小。若不及时清除线间故障，则其会一直隐藏在阵列中，导致更大的安全隐患[12]。

开路故障指光伏阵列中的某串任意一点发生断路，导致故障串开路，不产生能量。当开路故障发生时，阵列的电流瞬间下降为非故障串电流之和。由于开路故障前后最大功率工作点的电压相差不大，因此经过一个较短的时间，时序波形就趋于稳定，如图1（d）所示。

从上述分析可以发现，当光伏阵列发生故障时，电压、电流和功率的波形均会发生规律性变化。因此本文以功率波形为研究对象，通过机器学习算法，预测波形的发展变化。当实测波形和预测波形出现明显差异时，即判定发生故障，记录故障发生的时刻，并以此作为故障录波的启动判据。

2 方法的提出

2.1 数据预处理

考虑到不同模组参数的差异及光伏阵列规模的不同，需要对采集到的电压、电流数据进行标准化预处理以提高方法的适应性。本文将时序电压、电流分别除以在标准测试条件（standard test condition, STC）（1 000W/m2, 25℃）下的阵列开路电压oc和阵列短路电流sc，得到标准化后的电压、电流值，再将标准化后的电压、电流相乘则得到功率的标准化值。其表达式为

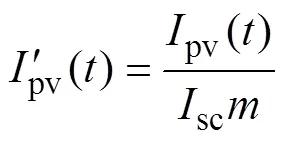
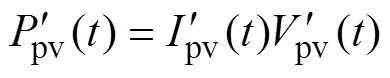
2.2 极限学习机

极限学习机[13]网络结构如图2所示，其为单隐含层前馈神经网络与随机学习相结合的产物。ELM随机生成输入层与隐含层之间的权重与偏置，一旦确定就不再改变。隐含层与输出层之间的权重和偏置则是通过矩阵变化求解，无需多次迭代计算。ELM在学习过程中无需耗时调整网络参数，学习速度极快，需要的计算内存很少。ELM网络模型的训练过程可描述如下。

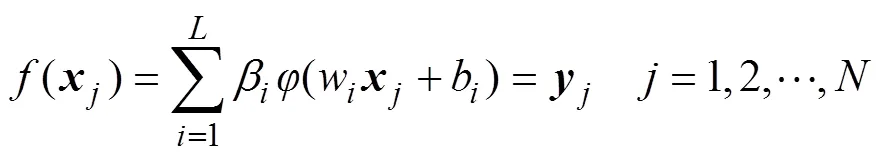
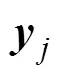
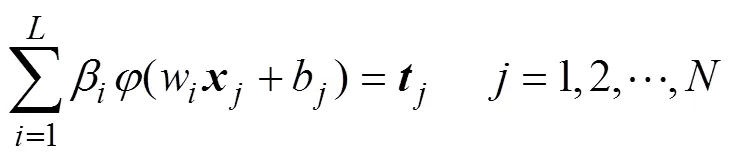
式（6）可以简化为

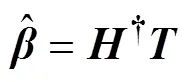
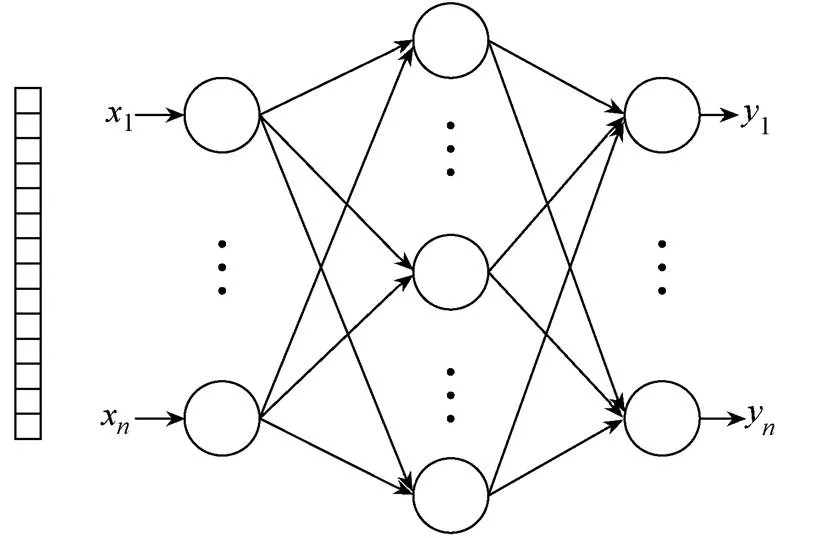
图2 极限学习机网络结构

2.3 波形相关系数

相关系数是一种用于表征变量之间变化关系的数学统计指标[14]，最早由统计学家卡尔·皮尔逊设计，包含标准差和协方差。两变量之间的皮尔逊相关系数为

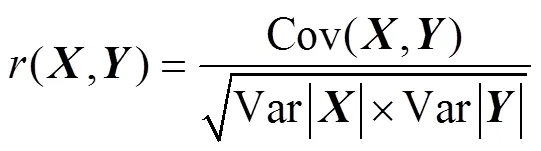
2.4 光伏阵列故障诊断方法

正常情况下，光伏阵列一般运行在电压、电流相对稳定的状态下。在这种情况下，功率波形短时间内基本保持在一个较小的范围内波动。而当光伏阵列发生故障时，功率波形在短时内会出现明显的下降趋势。基于此，本文提出基于ELM功率预测结合相关系数的光伏阵列故障快速诊断方法。通过将正常运行的功率数据作为ELM的训练样本，生成一个功率预测模型，实现正常运行情况下的短时功率预测。在正常运行时，由于ELM所输出的功率预测值与实际值之间存在强相关，则相关系数值较大。当故障出现时，预测模型输出的是正常状态的预测值，则预测值与实际值的相关性变低，相关系数会出现明显的下降。故障诊断流程如图3所示，具体如下：

1）以一定的采样率采集光伏阵列的电压、电流。

2）按式（1）～式（3）进行数据标准化处理。

3）使用标准化后的时序功率训练一个实现短时功率预测的模型。

4）求取功率预测值与实际值之间的皮尔逊相关系数。

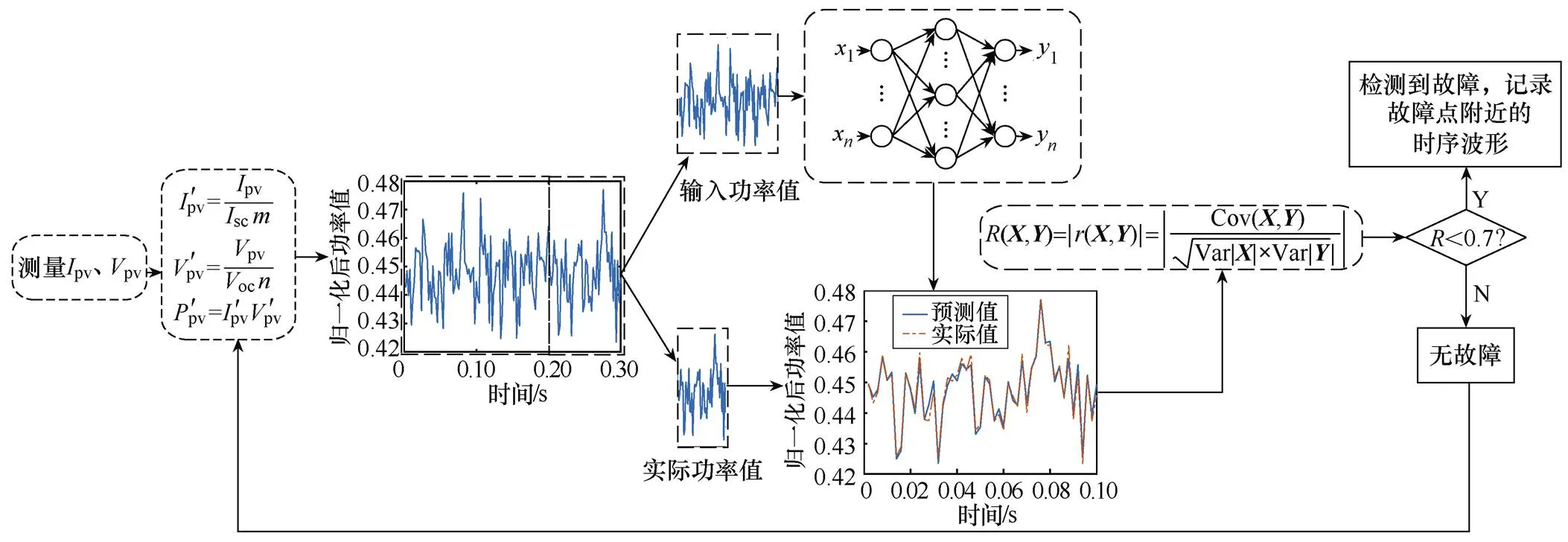
图3 故障诊断流程

3 实验验证

3.1 实验平台概述

光伏系统实验平台由光伏阵列、直流汇流箱、逆变器、交流电源和数据采集模块组成。光伏阵列的规模为2×12，即2串列并联，每串列有12块光伏模组，装机容量为6.48kWp。标准测试条件下的光伏系统技术参数见表1，实验场景如图4所示。在本文中，通过霍尔传感器将阵列电压与电流转换为小电压信号；NI 9220采集卡将电压模拟信号转换为数字信号；NI cDAQ—9185承担NI 9220采集卡和PC端之间的数据交互角色；使用LabView和Python编写相关程序。

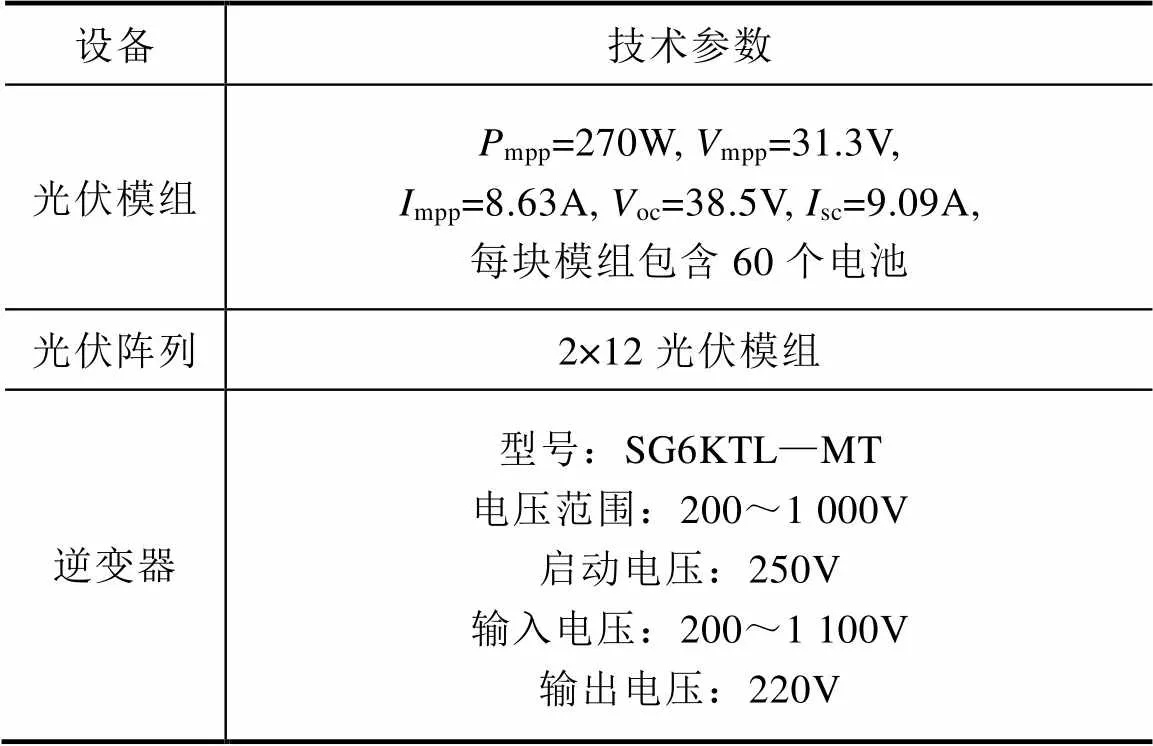
表1 标准测试条件下的光伏系统技术参数

正常类别的样本由辐照度稳定的样本和辐照度快速变化的样本组成；通过硬纸板对任意串任意模组进行遮挡以模拟部分遮阴；在任意时刻断开直流汇流箱中任意一串的空气开关以模拟开路故障；利用“Y”型接头及短路发生器（固态继电器）在某一时刻连通阵列中两个不同电位点以模拟线间故障。实验在200～900W/m2的辐照度和20～50℃的环境下完成。总计获得了448个样本，其中正常样本144个、部分遮阴样本100个、开路故障样本102个、线间故障样本102个。数据采样率为500Hz，时间窗口为0.2s。

图4 光伏实验场及故障模拟实验场景

3.2 R的阈值设置

将实验中采集到的100个正常运行样本作为训练集对极限学习机进行训练，其余44个正常样本及304个故障样本用于测试所提方法的性能。极限学习机神经元使用300个，激活函数采用Sigmoid。以0～0.15s内功率波形的数据作为ELM的输入数据，ELM的输出数据则为0.15～0.20s内的预测功率数据。通过分析功率预测波形同实测波形之间相关系数的变化关系来决定故障辨识的阈值。

1）正常状态

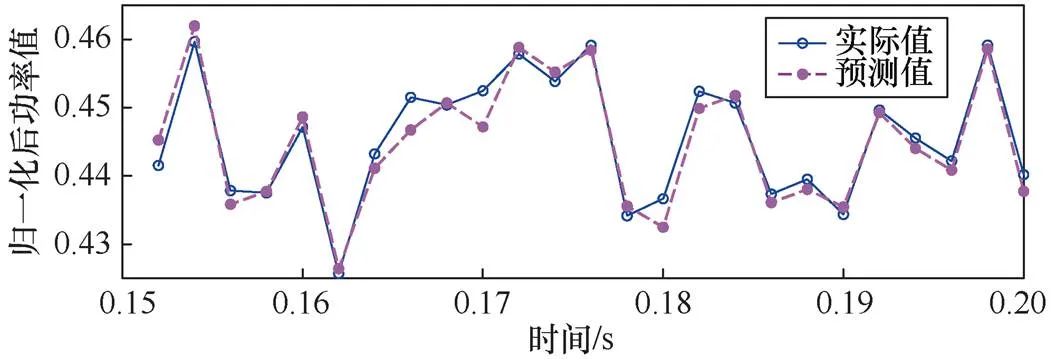
图5 正常状态下的功率曲线

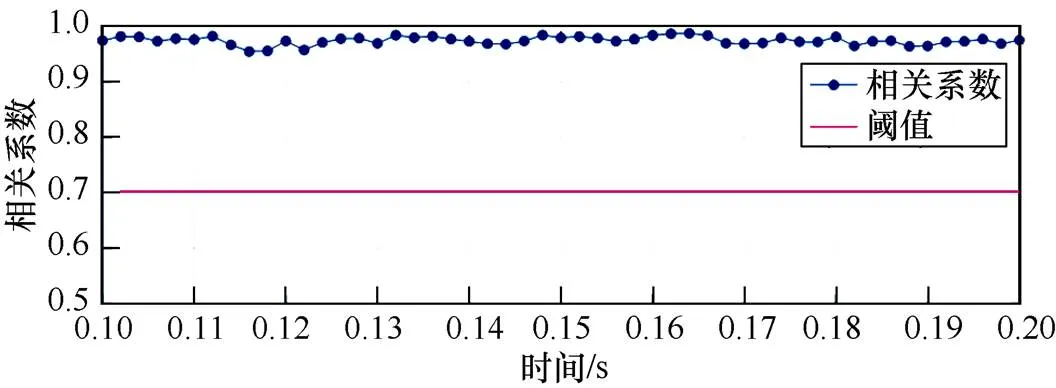
图6 正常状态下50个检测周期的相关系数变化

2）线间故障

在线间故障中，失配比越小，故障的严重程度越低，检测难度越大。为此，本文直接使用在本实验环境下能够获得的最低失配比（一个模块失配）的故障样本进行测试。

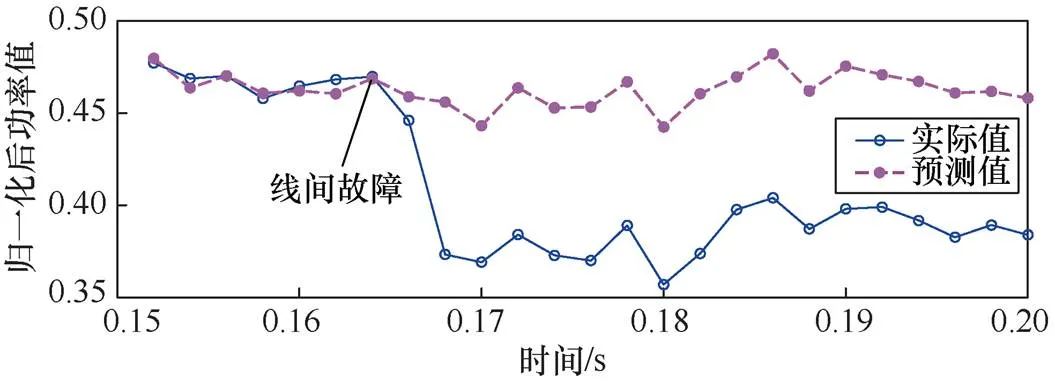
图7 线间故障下的功率曲线

图8 线间故障下50个检测周期的相关系数变化

3）开路故障

开路故障为光伏阵列故障中较为严重的一种，相对而言更容易检测。开路故障下的功率曲线如图9所示。从图9可以看出，预测值与实际值之间变化趋势显著不同。故障发生前，预测值与实际值较为近似；故障出现后，实际功率输出突然下降，而预测功率值仍然保持在0.45附近波动。

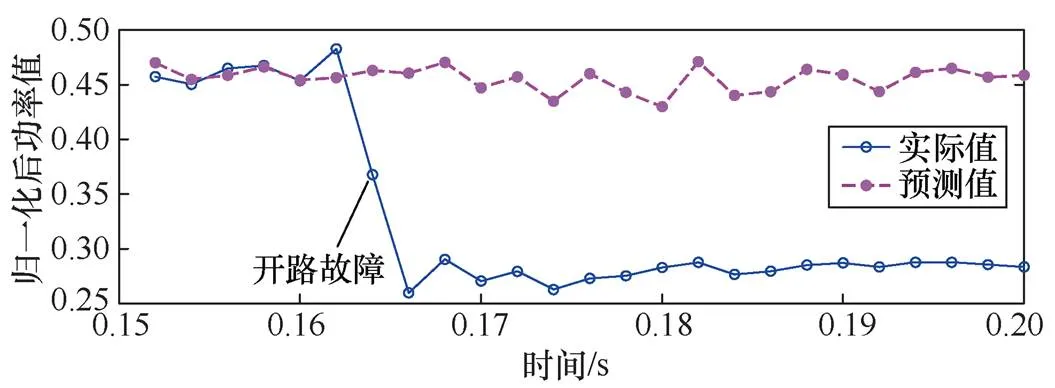
图9 开路故障下的功率曲线

开路故障下50个检测周期的相关系数变化如图10所示。在图10中，在0.164s前相关系数都高于0.85，而在0.166s开始突降，由前一刻的0.896 0瞬间降低至0.245 8，此后持续低于0.6，区分度极高。

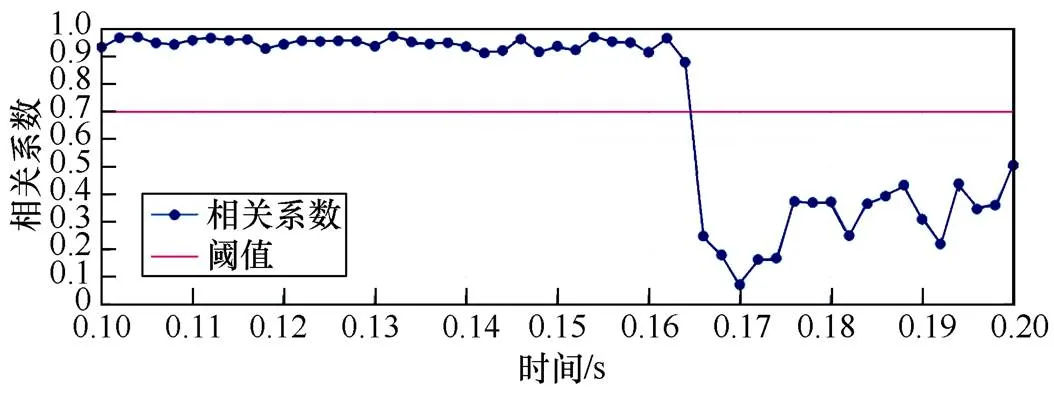
图10 开路故障下50个检测周期的相关系数变化

4）部分遮阴

在光伏阵列的故障中，部分遮阴是相对较难检测的。原因在于其不存在突变量，故障暂态的时序波形变化较为缓慢，并且功率变化幅值较小，远不及线间故障和开路故障，极易与正常状态混淆。部分遮阴下的功率曲线如图11所示。在图11中，故障出现在0.162s。故障发生后，功率实际值逐渐下降。预测值与实测值逐渐出现偏差。

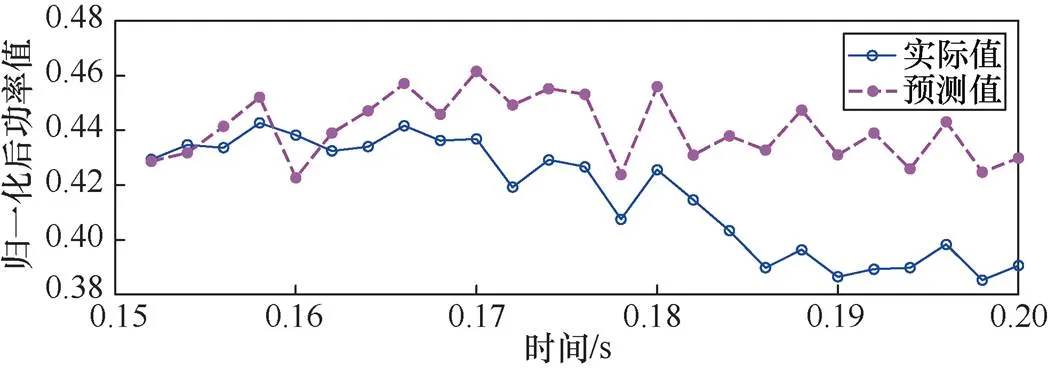
图11 部分遮阴下的功率曲线

部分遮阴下50个检测周期的相关系数变化如图12所示。在图12中，0.10～0.162s期间的相关系数都在0.9以上波动。在0.162s发生部分遮阴故障后，相关系数开始逐渐减小。在0.168s时，相关系数减小到0.641 2，此后，相关系数持续低于0.7。不同于前述的开路和线间故障，部分遮阴发生后，相关系数不会突降，而是逐渐减小，并且减小程度也不如前两者。但本文所提方法仍然能够有效检测到部分遮阴故障。

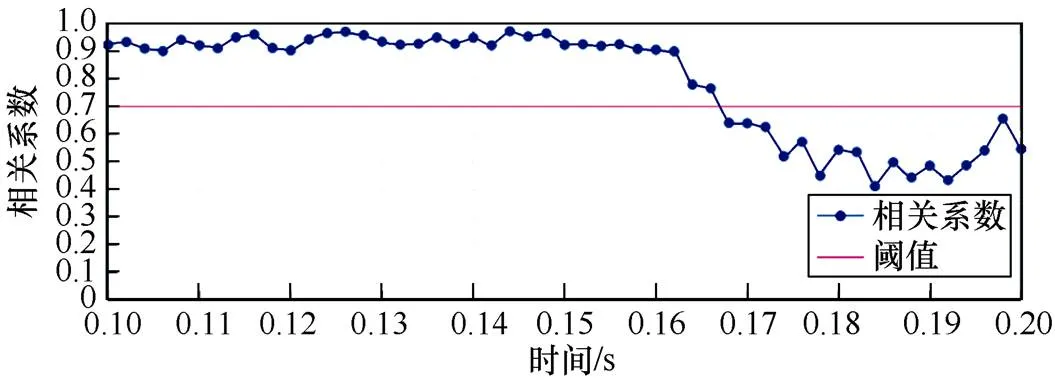
图12 部分遮阴下50个检测周期的相关系数变化

3.3 结果与评估

由于所提方法主要实现光伏阵列的故障检测，以作为录波启动的判据，因此需要尽可能地降低硬件需求，实现最快速的故障判断。为此，在原算法的基础上，需要考虑滑动窗口长度及滑动步长的选择。滑动窗口的长度关系到ELM运行速率，窗口越长则所需计算的数据越多，影响故障检测的速率；窗口越短则难以准确地获得预测值，预测结果的不准确将进一步降低方法的准确率。滑动步长则关系到故障检测的周期，滑动步长越短，检测周期也越短，对硬件要求越高；滑动步长越大，则故障暂态波形难以有效填充整个预测值的窗口，导致预测准确率下降。事实上，预测精度越高，预测功率和正常状态下的实测功率吻合度就越高，正常状态被误判的几率就越小，故障识别的成功率也越高。

为了测试不同长度滑动窗口下所提方法的故障检测性能，本文对上述304个故障样本进行测试，不同时间窗口的准确率及运行时间见表2。可以看出，0.2s长度的滑动窗口表现出最优的性能，判断总准确率为99.37%，与窗口长度为0.4s、0.7s的准确率相同，而运行时间却比上述两者更短。当窗口长度为0.1s时，所提方法的故障检测准确率出现明显的下降。综上，本文以0.2s作为所提方法的滑动窗口长度。

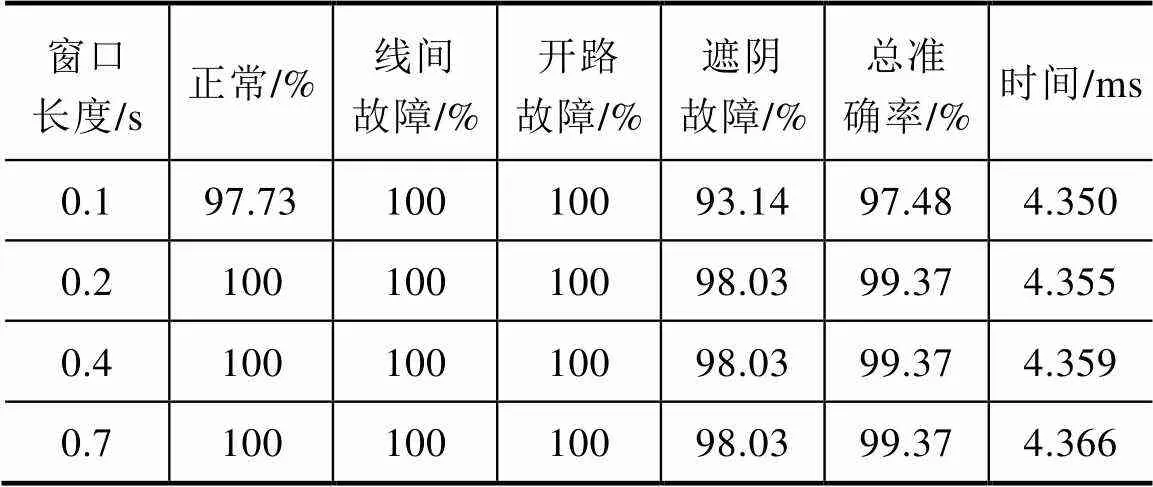
表2 不同时间窗口的准确率及运行时间

本文故障检测模型的运行环境为：Windows操作系统，i5—8300H的CPU，内存8G，集成显卡。运行时间由数据预处理、ELM功率预测、相关系数计算三部分组成。从表2可以看出，本文所提方法单次运行时间十分短，仅使用4.355ms。本文方法的采样率为500Hz，两个数据点采样间隔时间为0.002s，因此最小的滑动步长为6ms。

4 结论

针对光伏阵列故障诊断方法在实际应用中缺乏故障录波启动判据的问题，本文提出了一种基于极限学习机和皮尔逊相关系数的故障快速检测方法。所提方法通过极限学习机模型预测了未来功率波形的变化，并通过波形相关系数的下降特征判定故障发生的时刻。经实验验证，所提方法能准确辨识出线间、开路、遮阴等故障，准确率达到99.37%，运行时间仅4.355ms，达到实际应用要求。

在本文中，逆变器的MPPT启动，可能会导致算法将其误判为故障。但是作为故障录波的启动算法，追求的是快速性，而非极高的辨识准确率。位于其后端的故障分类算法可以将MPPT启动的样本辨识出来[15]。因此，所提方法满足作为故障启动判据的要求。在后续的研究中，将重点考虑将算法部署到单片机或树莓派上，以测试其在实际应用中的适应性。

[1] 国家能源局. 国家能源局2021年一季度网上新闻发布会文字实录[EB/OL]. [2021-01-30]. http://www.nea. gov.cn/2021-01/30/c_139708580.htm.

[2] 陈国灯, 林培杰, 赖云锋, 等. 基于电流时间序列的光伏故障在线监测系统[J]. 电气技术, 2018, 19(6): 20-25.

[3] PEI Tingting, HAO Xiaohong. A fault detection method for photovoltaic systems based on voltage and current observation and evaluation[J]. Energies, 2019, 12(9): 1-16.

[4] 王元章, 吴春华, 周笛青, 等. 基于BP神经网络的光伏阵列故障诊断研究[J]. 电力系统保护与控制, 2013, 41(16): 108-114.

[5] 程泽, 董梦男, 杨添剀, 等. 基于自适应混沌粒子群算法的光伏电池模型参数辨识[J]. 电工技术学报, 2014, 29(9): 245-252.

[6] GEORGIJEVIC N, JANKOVIC M, SRDIC S, et al. The detection of series arc fault in photovoltaic systems based on the arc current entropy[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5917- 5930.

[7] ZHAO Ye, PALMA J D, MOSESIAN J, et al. Line-line fault analysis and protection challenges in solar photovoltaic arrays[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3784-3795.

[8] PILLAI D S, NATARAJAN R. An MPPT-based sensorless line-line and line-ground fault detection technique for PV systems[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8646-8659.

[9] 孙祥晟, 陈芳芳, 贾鉴, 等. 基于经验模态分解的神经网络光伏发电预测方法研究[J]. 电气技术, 2019, 20(8): 54-58.

[10] HARIHARAN R, MANICKAM C, ILANGO G S, et al. A method to detect photovoltaic array faults and partial shading in PV systems[J]. IEEE Journal of Photo- voltaics, 2016, 6(5): 1278-1285.

[11] MOHAMMED K A, FAISAL K, JAY J, et al. A comprehensive review of catastrophic faults in PV arrays: types, detection, and mitigation techniques[J]. IEEE Journal of Photovoltaics, 2015, 5(3): 982-997.

[12] GAO Wei, WAI Rongjong, CHEN Shiqun. Novel PV fault diagnoses via SAE and improved multi-grained cascade forest with string voltage and currents measures[J]. IEEE Access, 2020(8): 133144-133160.

[13] HUANG Guangbin, ZHOU Hongming, DING Xiaojian, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man & Cybernetics Part B, 2012, 42(2): 513-529.

[14] 师愉航, 汲胜昌, 张凡, 等. 变压器油箱表面运行变形振型特性研究[J]. 电工技术学报, 2019, 34(5): 202-209.

[15] CHEN Shiqun, YANG Gengjie, GAO Wei, et al. Photovoltaic fault diagnosis via semi-supervised ladder network with string voltage and current measures[J]. IEEE Journal of Photovoltaics, 2021, 11(1): 219-231.

A fast fault diagnosis method for photovoltaic array via extreme learning machine and Pearson’s correlation coefficient

CHEN Shiqun1GAO Wei2CHEN Xiaoqi2TU Yanzhao2YANG Yan3

(1. Fuzhou Changle District Electric Power Supply Branch of State Grid Fujian Electric Power Co., Ltd, Fuzhou 350202; 2. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108; 3. Faculty of Automation, Huaiyin Institute of Technology, Huaian, Jiangsu 223003)

The failure of the photovoltaic (PV) array can cause energy loss and even cause power supply interruption or fire accident. Therefore, it is very important to identify the fault quickly. A new fast fault diagnosis method for PV array is proposed to quickly perceive the fault and the time of fault occurrence in this paper. Based on the analysis of the signal variation rule of PV array traditional faults, a prediction model of extreme learning machine (ELM) is investigated to train the power waveform during normal operation, which is adopted to predict the short-time power variation. Then Pearson’s correlation coefficient of measured waveforms and predicted waveforms are calculated. If the PV array fails, the correlation coefficient will be below the threshold, thus identifying the occurrence of the fault. Experimental results show that the proposed method has strong ability of fault identification, and the accuracy reaches 99.37%. The fault identification time of the proposed method is only 4.355ms, and it can be used as the start-up method of PV array fault recording.

photovoltaic array; fault recording; extreme learning machine (ELM); Pearson’s correlation coefficient

江苏省住房和城乡建设厅指导项目（2019ZD001287）

江苏淮安市科技局自然科学研究计划项目（HAB201905）

2021-02-26

2021-03-31

陈世群（1995—），男，福建福州人，硕士，研究方向为新能源故障诊断研究。