高中物理力学学习中数学方法的应用
赵娟
摘要:力学是高中物理学科中的重点知识,这一部分内容是物理学科的一个核心,也是学生在以后深入学习物理知识的基础,所以必然要加强物理力学教学,让学生真正扎实地掌握这部分内容。高中物理教师在对教学模式进行创新探索的过程中,要注重数学方法的合理运用,这不但可以促使学生正确计算数值,更重要的活跃了思维,提高了解决物理问题的能力。在具体教学过程中,教师要从力学教学实际情况出发,关注解析法、极限法和函数法的灵活运用,实践证明,这都将有助于提高学生的物理学习水平。本文主要围绕了高中物理力学学习中数学方法的应用进行了探究,以供参考交流。
关键词:高中物理;力学;数学方法;应用
引言
随着目前教育行业中的课程改革不断深入,各科的联系也逐渐增强,在物理和数学两个学科中体现的尤其明显。数学方法在物理特别是力学中的应用越来越多,这对高中学生在学习方面提出了更高的要求,也为高中物理教师的教学活动开展提出了新的考验,是对传统教学模模式的一次革新和尝试。在把数学知识应用在物理力学中时,必须要把两者有效结合起来,使数学思维和方法得到充分体现,实现数学知识点和物理知识点的相互转化。我们必须具体了解数学知识与高中物理力学的有机联系,掌握数学学科和物理学科的基础知识,才能把数学知识实际应用在物理问题的解决上。
1数学方法在高中物理力学学习中应用的可行性
一方面,借助数学方法可以帮助理解物理概念。高中物理知识比较复杂抽象,尤其是很多物理概念对于学生来说不容易理解,所以可以引入运用数学方法帮助理解学习。比值定义法就是一种重要的方法,充分体现了数学思维,主要是通过分析某个物理概念与其他物理量的相互关系,这可以更好地反映出数形关系[1]。例如,“密度”是某种物质的质量与体积的比值,“加速度”是速度变化量与发生这一变化所用时间的比值。再比如,对于一些物理定理的理解,也可以借助数学思维的阐释式进行辅助理解,提高了物理学习效率。
第二,利用借助数学方法可以推导物理概念。对于高中物理有一些问题,通过数学知识不仅能阐述问题的由来,还能阐述问题的发展路径。以“直线运动”知识为例,可以应用数学代数方法构建三角模型,以此为依托把握直线运动的运动规律。除了代数方法、三角方法之外,经常要应用数学矢量方法,对位移、速度等进行大小和方向的判断。高中物理学科中有许多基本公式,这些基本公式可以推导出其他关系式,对物理解题起着至为关键的作用。我们应用数学方法得到基本公式和其他关系式,能够深入理解物理概念与物理概念之间的关系,让物理学习简单起来。
2高中物理力学学习中数学方法的应用
2.1解析法的应用
在学习高中物理力学知识时,经常要对物理运动轨道进行分析。一切物理理论知识都是从物理实验中衍生而来的,如果没有物理实验,理论知识就会成为无本之末。因此,我们还需要关注物理实验,通过物理实验总结物理定律、理解抽象物理概念等。解析方法是高中物理力学学习的常用数学方法,可以对物理问题进行解析和推导,得到具象的解析结果[2]。以“抛物体运动”为例,就可以应用数学解析方法,对抛物体运动现象进行科学观察对物体以一定的初速度向空中抛出,仅在重力作用下物体所做的运动叫做抛体运动,分为竖直上抛运动、竖直下抛运动、平抛运动和斜抛运动。我们可以把理论内容和生活实践联系在一起,对生活中的抛物体运动现象进行归纳总结,从简单实验中分析抛物体运动的初始速度等。
2.2极限法的应用
极限法在高中物理力学中的应用比较普遍,比如可以把力学中的倾角变化的倾斜面转换为水平面或者垂直面,从而进一步把物理力学中较为复杂的问题转化为比较简单的问题。另外,还可以把正在运动的物体看作是静止的物体,把非理想物理模型转换成理想的物理模型,把变量转换成固定的数值等[3]。从实际运用方面来说,数学知识中的极限法是高中物理中应用最普遍的知识方法,面对许多需进行定性分析的物理力学问题,运用极限法可以使解决问题的过程中避免许多不实用的繁琐运算,一般只进行比较简单的运算就可以解决问题得出结论。我们在学习过程中却往往比较容易忽视极限法的运用,因此无论是教师还是我们学生,都应该加强对极限法的重視。我们应该遵循教师的教导,把极限法具体应用到力学实际解决当中,不断开阔思维,提高解决问题的能力。一元二次函数的极值问题应用范围很广,比如“在相遇问题中的速度加速匀速运动的物体,求什么情况下两个物体相距最远?”就可以有效解答。
2.3函数的应用
一般情况下,物体的物理量是随时间而进行变化的,所以物理量之间会形成各种各样的函数关系,如果状态平衡固定,那么函数就会转化成有关固定量的关系方程。在物理力学相关问题的解决过程中,确定适当准确的函数是首先需要重视的问题。在物理中比较常见的函数包括,正反比例函数,三角函数,二次函数等,要充分利用函数的优势,化繁为简,根据物理力学过程的具体特征正确选择使用函数[4]。
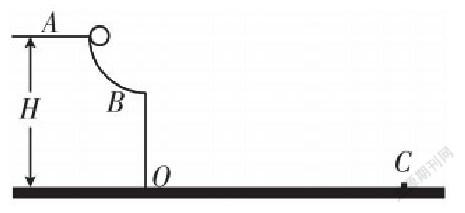
例:如图,在竖直平面上有一个1/4圆弧的光滑轨道,圆弧半径是R,OB顺着竖直方向,上端A底距地面的高度为H。一个质量m的小球,在A点由静止释放。在不用考虑空气阻力情况下,当H为何值时,小球的落地点与B的距离最远?
在解答该问题时,可以根据平抛运动的规律求出水平距离的表达式,再结合二次函数求极值得出小球的落地点与B的距离最远时H的值。
结语
总之,在高中物理力学的学习过程中,我们必须加强对自身的严格要求,充分发挥数学方法在物理中的积极作用,充分利用数学方法和思维方式,综合分析问题,认真思考提出合理的解决方案,要把数学知识和物理力学有效结合起来,真正实现物理问题和数学问题的相互转化,从而高效解决物理力学的有关问题。
参考文献:
[1]陈文君.高中物理力学学习中数学方法的应用[J].数码世界,2017(11):76.
[2]蒋雷.高中物理力学学习中数学方法的应用[J].同行,2019(14):45-46.
[3]宫晨羽.浅析高中物理力学学习中数学方法的应用[J].考试周刊,2018(5):99-101.
[4]李自强.谈谈新课改下高中物理力学的教学方法[J].社会科学:引文版,2019(7):125.

