碳纤维复合材料缠绕铝合金管准静态轴向压缩的数值模拟

董 帆，马其华,，甘学辉，周天俊

(1.上海工程技术大学机械与汽车工程学院，上海 201620；2.东华大学，纤维材料改性国家重点实验室，上海 201620)

0 引 言

纤维增强复合材料因比强度高、比模量大、可设计性强等优点正在成为某些金属结构件的替代材料[1]；但是成本高以及其在受到冲击载荷时易产生不稳定局部屈曲和脆性断裂等问题，也影响到了该材料在金属结构件中的应用。为了提升轻量化效果并兼顾成本和结构性能，金属-碳纤维复合材料相结合的混合材料应运而生[2-3]。碳纤维复合材料缠绕铝合金薄壁管(简称Al-CFRP混合管)作为典型的混合材料结构件正被广泛研究，以便应用于汽车、航空等领域。采用有限元仿真分析方法研究Al-CFRP混合管的抗撞性能可有效节约试验成本，更好地实现优化设计。

对于混合管准静态轴向压缩的有限元分析，不同研究在CFRP层建模、黏接单元的模拟以及失效判定准则等方面各有特点。单层壳模型是一种模拟复合管破碎行为的高效方法，适用于强调峰值载荷与平均载荷预估整体吸能的情况；但是该模型无法模拟复合管的分层[4-5]。多层壳模型对于混合管压缩变形模式及能量吸收能力的预测更为准确。SHI等[6]、REUTER等[1]和KIM等[7]在仿真研究中采用多层壳单元模型对混合结构进行模拟，通过与试验结果对比可以看出多层壳单元模型能够模拟混合结构复杂的失效模式，并且得到的耐撞性能指标与试验值也很接近。KATHIRESAN等[8]采用多层壳有限元模型，通过网格细化，提高了混合管数值分析的准确性和效率。对于胶黏关系，ZHU等[9]依托多层壳单元提出了一种新的建模方式，通过偏置壳单元生成胶黏实体模仿混合管中胶黏关系。DLUGOSCH等[10]综合网格尺寸与边界条件，对比了“Tie”绑定与“Cohesive”两种黏接属性的差别与局限性，并通过试验证明两种方法的可信度。朱国华[11]在前人研究基础上考虑混合管的层间胶黏性质，建立单层壳与多层壳仿真对比模型，分析了混合结构的损伤模型，发现多层壳单元可以更好地模拟压缩吸能机制。对于CFRP各向异性的力学特性及复杂的失效模式，合理的失效准则是开展耐撞性能设计的前提。目前，PAM-CRASH、LS-DYNA和ABAQUS等商业软件依托各自内嵌的材料本构方程和失效准则，在复合材料的损伤计算方面各具特色[12-14]。其中，ABAQUS软件采用Hashin失效判别准则和演化模型，将材料破坏分为纤维拉伸破坏、纤维压缩破坏、基体拉伸破坏和基体压缩破坏4类，同时结合内聚单元的牵引分离定律，在复合材料仿真方面得到广泛应用[15-16]。铝合金管与CFRP形成的混合薄壁管具有双重材料特性，铝合金与CFRP以及CFRP层与层之间的黏接强度难以确定。目前，研究人员在建模时仅考虑到材料性能的影响，忽略了材料比例，尤其是在金属-复合材料混合结构件上，CFRP多层缠绕和少层缠绕对建模的影响。

因此，作者以缠绕10层和3层CFRP的Al-CFRP混合管为研究对象，使用ABAQUS/Explicit软件及自带的Hashin失效准则[17]及内聚力黏接单元建立3种不同单元类型的模型，对比3种模型对混合管准静态轴向压缩变形和吸能特性的仿真精度；为解决模型选择中多参数的相对误差呈现相互矛盾的问题，对各参数进行权重分析，定量评估了多层和少层缠绕管的候选模型，为金属-复合材料混合结构的设计与仿真提供参考。

1 试样制备与试验方法

铝管选用外径为37 mm，壁厚为1.5 mm的6063铝合金管，密度为2 700 kg·m-3，弹性模量为67 000 MPa，泊松比为0.33，屈服强度为225 MPa；外层材料为CFRP，碳纤维与树脂分别为日本东丽株式会社的T700-12K碳纤维和浙江百合的BAC172环氧树脂。使用砂纸打磨铝管外表面，并在丙酮中浸泡清洗。将铝管安装在缠绕机上，通过湿法缠绕工艺将CFRP预浸料带缠绕在铝管上，纤维基础预载荷为89.1 N。为了保证预浸料带中树脂的均匀性，树脂槽温度保持在36 ℃左右。将缠绕好的混合管用真空袋密封后放置于烘箱中，加热到120 ℃固化2 h，自然冷却后取出加工成所需长度。共制作2种CFRP层数的试样，试样A为缠绕10层CFRP的混合管，CFRP缠绕角度为[±450°/90°/±45°/90°/±45°/90°/45°]；试样B为缠绕3层CFRP的混合管，其缠绕角度为[±45°/90°]。两种试样的尺寸如图1所示。

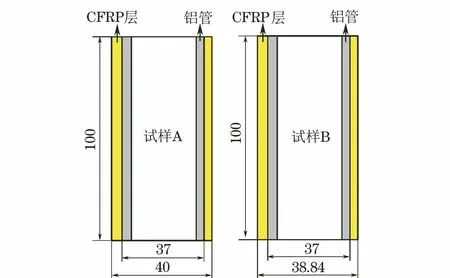
图1 Al-CFRP混合管试样尺寸Fig.1 Dimension of Al-CFRP hybrid tube sample

根据GB/T 1448-2005，采用深圳万测试验设备有限公司的WANCE 605A型万能试验机对试样进行准静态轴向压缩试验。考虑到试验误差和CFRP性能的各向异性，为保证动态试验结果的准确性，试验过程通过位移进行控制，拉伸速度恒定为2 mm·min-1；为了便于比较，将最终破碎位移设置为试样长度的60%。通过力-位移传感器记录试样承载过程的载荷-位移曲线。

2 轴向压缩有限元仿真模型

2.1 混合管损伤模型

损伤准则是评价材料性能的关键。Hashin失效准则考虑纤维与基体的多模式损伤演化，结合刚度矩阵引入折减系数，按照不同的损伤模式对发生损伤单元的部分刚度进行瞬间折减，可以更好地模拟纤维失效承载力的变化趋势。因此作者以Hashin失效准则为基础，建立Al-CFRP混合管损伤模型。在仿真过程中，当材料的应力状态满足失效条件后，ABAQUS软件内部会剔除退化的单元，下一个碰撞的接触单元将自动由与剔除单元享有共同节点的单元代替，然后继续判断失效，最终完成整个破坏过程的仿真和计算[18]。

2.1.1 层内损伤

层内损伤是通过单元不同方向的破坏情况进行判断的，用损伤变量来量化纤维和树脂基体的拉伸以及压缩破坏。在模拟中使用Hashin失效准则对复合材料层内损伤进行评估[17]，其失效准则表达式为

纤维拉伸失效

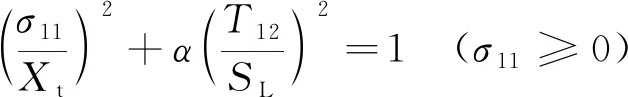
(1)

纤维压缩失效

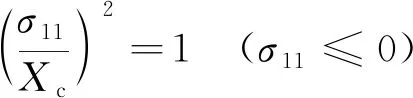
(2)

基体拉伸失效

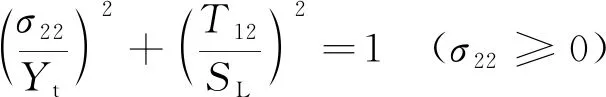
(3)

基体压缩失效

(σ22≤0)

(4)

式中：σ11，σ22，T12分别为沿纤维方向、垂直于纤维方向以及剪切方向上的有效应力分量；α为剪切应力对纤维拉伸失效判据的影响系数(设定α=0)；Xt为轴向抗拉强度；Xc为轴向抗压强度；Yc为横向抗压强度；Yt为横向抗拉强度；SL为轴向剪切强度；St为横向剪切强度。

Hashin准则的双线性渐进损伤模型的前半段为弹性拉伸，后半段为线性损伤。I型模型的损伤变量dI的表达式定义为

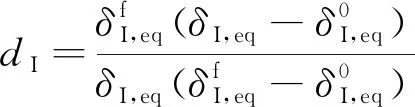
(5)

式中：δI,eq为等效位移，上标0表示损伤起始，f表示材料发生完全破坏。

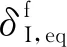
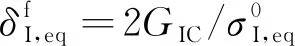
(6)

式中：σI,eq为等效应力。

2.1.2 层间损伤

层间的本构响应是使用内聚接触法建模的。该方法基于牵引分离法则定义，包括相应的破坏准则和演化。在分层之前，层间行为被认为是线弹性的。假定法向和剪切牵引分量在弹性范围内是不耦合的，则弹性行为可以定义为

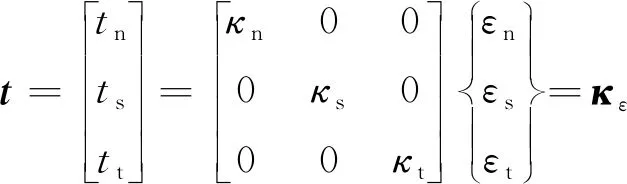
(7)

式中：t为牵引应力矢量；t为对应开裂模式下的牵引应力；下标n，s和t分别对应张开型、滑开型和撕开型3种开裂模式；ε为应变分量；κε为相互作用的刚度矩阵;κ为初始刚度。

分层的起始通常是在混合模式载荷作用下发生的。CUI等[19]的研究表明，在混合模式载荷作用下，各应力分量之间的耦合作用对损伤的起始和扩展影响较大。因此，作者采用了混合模式下描述黏接域损伤起始和扩展的损伤模型，模型详见文献[19]，其损伤准则表达式为

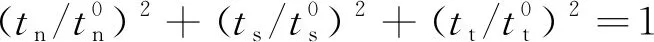
(8)

当函数的值达到1时，损伤按照损伤演化定律发生增长，表达式为

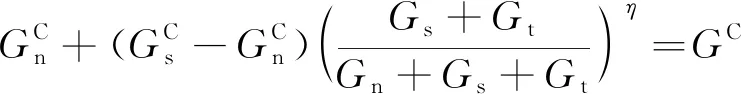
(9)

式中：G为断裂能，上标C表示临界；η为内聚属性参数。

以文献[20]中相似材料的层间性能参数作为Al-CFRP混合管层间损伤模型参数，详见表1，表中ρ为密度。

表1 内聚力分层剥离的层间性能参数

2.2 单层壳模型

采用非线性有限元软件ABAQUS/Explicit，分别以铝管和CFRP管实现混合管的两层壳建模，CFRP层的壳模型不考虑实际碳纤维铺层数，将N层碳纤维预浸料铺在一层壳上面,损伤演化规律主要取决于单元尺寸。考虑到计算效率，CFRP管和铝管均使用大小为2.0 mm×2.0 mm，类型为S4R(四节点曲面壳单元)的网格。CFRP层的铺层方式按照2种试样实际铺层角度设置，选中赋予铺层信息的CFRP壳单元，这一元素下的铺层堆叠方式如图2所示，试样A中每层厚度为0.15 mm；试样B中每层厚度为0.36 mm。在底面处层合结构厚度方向的壳单元设置数个积分点，单层复合材料子层结构通过单个积分点来表示。根据显示计算的要求，这些元素形成了总质量矩阵，适用于分析大变形。混合管模型放置在上下刚性板(R3D4：四节点3D双线性刚性单元)之间，管上部受上刚性板平行于z轴的压缩力作用(除z轴方向全约束)，下部刚性板底部自由度全约束。铝管与CFRP管采用面面接触，CFRP管与上、下刚性板的接触采用通用接触，以避免仿真过程中出现单元的相互穿透，摩擦因数为0.3。

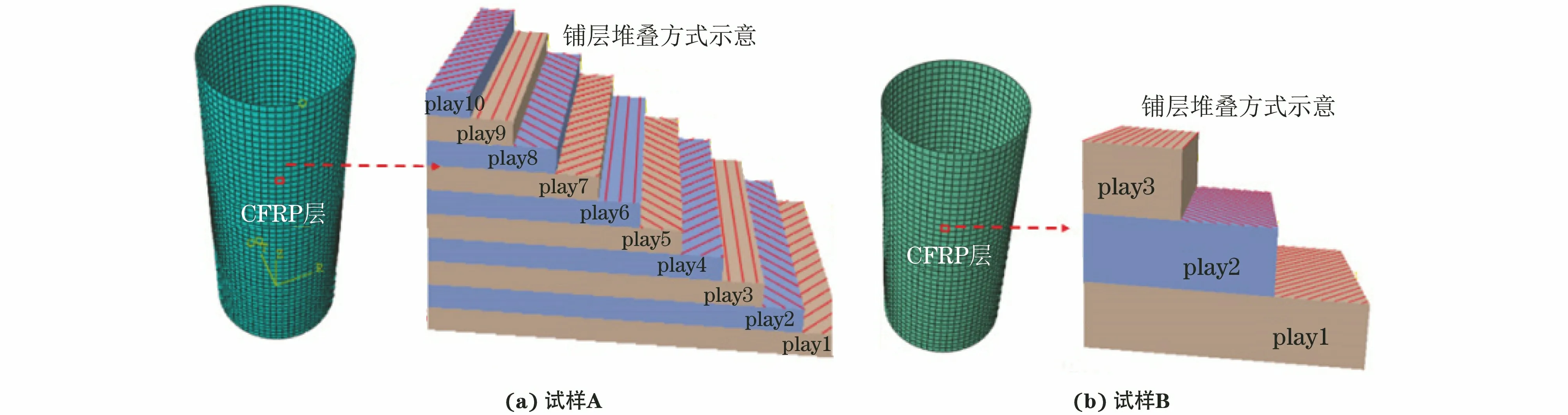
图2 单层壳模型中CFRP层结构示意Fig.2 Diagram of CFRP layer structure of single-layer shell model: (a) sample A and (b) sample B

2.3 多层常规壳模型

为了更精确地模拟Al-CFRP混合管在轴向作用力下的失效分层，采用一层实体单元(C3D8I：八节点六面体线性非协调模式单元)模拟铝层，按照实际铺层数建立壳单元(S4R)模拟CFRP层，且单层壳厚度与实际单层厚度相等。由于使用集成度降低的元素，因此需要沙漏控制防止复合管的元素过度变形。层与层之间通过内聚区元素(CZE)连接在一起，模拟铝管与CFRP层、CFRP各层之间的黏接。图3为黏性区域元素(COH3D8：八节点三维黏性单元)和材料层的黏结建模示意。CZE在一侧与一个外壳层共享其节点，并在另一侧将其节点绑定到另一外壳层模拟黏性区域平面内应力状态。此外，界面处的CZE还可以模拟板层之间(各CFRP层之间以及铝管和CFRP层之间)的接触行为。但是，当删除CZE(分层失败)时，将没有可用的区域来维持层与层之间的交互。因此，在CZE之间应用了附加的接触定义，设置了摩擦因数为0.3的一般接触。其余参数设置参照单层壳模型。

图3 多层常规壳黏性黏结建模示意Fig.3 Schematic of multi-layer conventional shell adhesive bonding modeling

2.4 多层连续壳模型

Al-CFRP混合管模型包含内层铝合金(C3D8I)和外层CFRP两部分，其中基于实体对每个CFRP铺层都建立连续壳单元(SC8R：八节点四边形平面通用连续壳单元)，并通过内聚力接触模型(COH3D)将各实体单元“层合”在一起，模拟层与层之间的分层破坏。这种模型具有实体元素的几何形状，但是其本构行为与常规壳体元素相似。考虑大变形及损伤尺寸的影响，使用网格尺寸为2.0 mm×2.0 mm的连续壳单元对混合管进行划分，层与层中间插入0厚度的黏接单元。

综上，建立的3种Al-CFRP混合管有限元模型如图4所示，建模方法对比见表2。

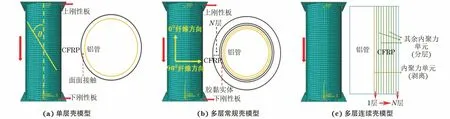
图4 Al-CFRP混合管有限元模型Fig.4 Finite element model of Al-CFRP hybrid tube: (a) single-layer shell model; (b) multi-layer conventional shell model;(c) multi-layer continuous shell model

表2 3种仿真模型建模方法对比

3 试验与仿真结果对比分析

3.1 压缩过程与损伤模式对比

由图5和图6可以看出，单层壳模型、多层常规壳模型和多层连续壳模型模拟得到的2种试样在压缩过程中的变形与试验结果较吻合。在单层壳模型仿真中，铝管在压缩过程中表现出钻石折叠的变形模式，外层CFRP表现出纤维的失效删除模式；当出现轴向与周向纤维破坏时，单层壳模型无法准确地模拟复合材料所显示的分层破坏以及与混合管共同承载情况。在多层常规壳模型仿真中，混合管上端首先出现应力集中达到峰值，随着压缩位移的增加，CFRP层首先出现分层现象，轴向纤维向外张开；在达到峰值载荷的同时，下端铝管发生微小变形，造成部分纤维撕裂，在压缩后段CFRP层因为铝管的限制向外扩展而脱离铝管，没有模拟出纤维夹杂在铝管褶皱中的状态。在多层连续壳模型仿真中，CFRP层的断裂与其分层紧密关联，分层将堆叠的实体分开，分离的实体单元容易变弱和断裂；仿真中部分CFRP脱离铝管，且计算收敛，删除了部分撕裂的纤维被压缩在铝管褶皱中的情况；在铝管起主导的后期承载过程中，不均匀的纤维承载导致混合管出现非轴对称折叠压缩形式。

试样B缠绕厚度较薄，在达到峰值载荷时可以在混合管上清晰地看到与轴向成45°方向的裂纹，并且混合管以此角度发生扭曲，在扭曲处纤维首先发生破坏。在多层常规壳模型仿真中，试样B下端首先发生变形，并迅速形成薄弱环节，但是其总体的变形过程与其他模型仿真结果无异；在试验中也存在此现象。

3.2 吸能特性对比

由图7结合图5、图6分析可知，试样的轴向压缩过程可以分为3个阶段：第一阶段为初始压缩过程中混合管的线弹性变形阶段；第二阶段混合管出现纤维撕裂继而发生塑性屈曲，混合管受弯矩作用产生的转角(塑性铰链)出现弯曲塌陷现象，载荷下降明显；第三阶段撕裂的内外片状纤维被埋入塑性铰链的凹部中，使得混合管顶部开始沿加载方向向外堆叠，之后载荷逐渐趋于稳定。3种仿真模型对于初始峰值载荷的预测较准确，但是由于不同模型在单元失效删除和黏接模型上的差异，仿真曲线在峰值载荷后出现不同程度的差异。

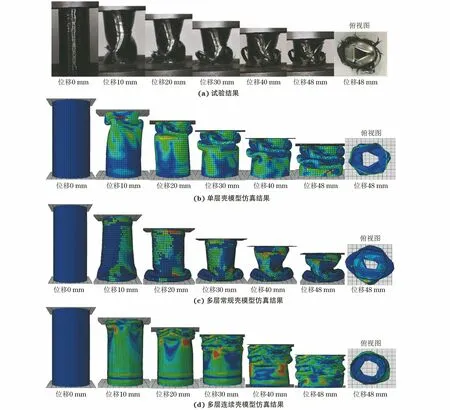
图6 试样B轴向压缩变形过程的试验与仿真结果Fig.6 Experiment (a) and simulation (b-d) of axial compression deformation of sample B: (b) single shell model simulation;(c) multi-layer conventional shell model simulation and (d) multi-layer continuous shell model simulation

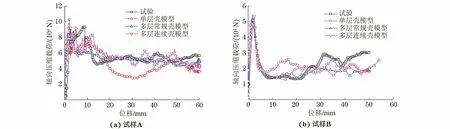
图7 试样轴向压缩载荷-位移试验曲线和仿真曲线Fig.7 Experimental and simulation curves of axial compression load vs displacement of samples: (a) sample A and (b) sample B

选用初始峰值载荷(PCF)、比吸能(SEA)、平均压缩载荷(MCF)作为设计过程中的压缩吸能指标。初始峰值载荷反映压缩载荷平稳前的最大载荷值，是评价结构性能的最重要指标之一；平均压缩载荷是压缩平稳阶段的平均载荷；比吸能则反映了单位质量材料的吸收能量，是考量结构吸能的核心指标。由表3可以看出：多层连续壳模型对试样A和试样B的轴向压缩行为预测的综合准确性最高，仅有对试样B峰值载荷仿真的相对误差大于5%；单层壳模型对试样A压缩行为预测的综合准确性不如多层常规壳模型，但是对试样B压缩行为预测的综合准确性与多层常规壳模型相当。

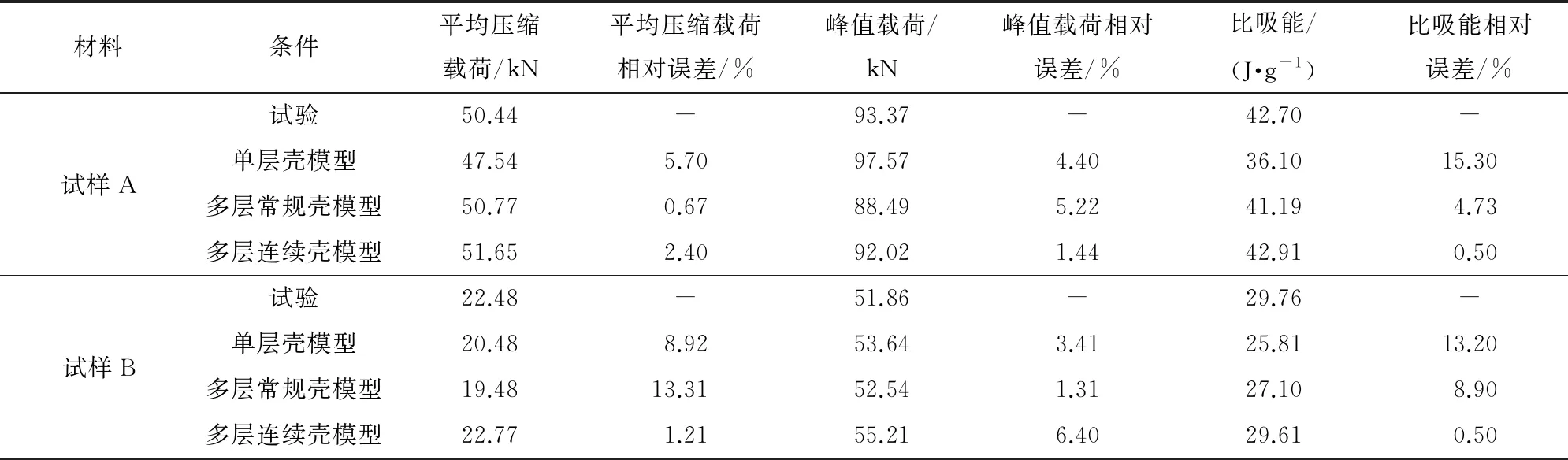
表3 3种仿真模型模拟结果与试验结果对比

建模方法的不同实际表现为单元类型的差异。单层壳模型的单元类型为S4R，采用减缩积分方式，包含沙漏模式控制，其仿真中可以看到明显的纤维撕裂现象，但由于忽略横向剪切变量与分层吸能的影响，比吸能明显低于试验结果；并且在仿真中，当试样周向破坏后对失效单元进行了删除处理，脆性断裂部分出现空隙，载荷下降，但当铝管铰链叠加在一起时，载荷又上升。

多层常规壳模型在S4R单元的基础上偏置生成实体，赋予黏接材料参数，同时绑定另外一层壳(共节点)模仿树脂黏接，在仿真中堆叠的壳单元在层内根据失效准则部分删除，刚度降低的同时低估了轴向压缩下的应力响应，因此不能准确模拟部分强度较弱但在渐进叠缩过程中夹杂在褶皱中的片状纤维，且由于达到峰值载荷时下端铝管发生微小变形，部分纤维撕裂，仿真得到试样A和试样B的峰值载荷与试验结果存在5.22%和1.31%的相对误差。

多层连续壳单元模型采用的SC8R单元考虑了剪切变形的影响，在仿真初期得到的峰值载荷与试验结果存在微小误差，这是由于仿真以理想塑性模型建模，不能准确反映材料缺陷；此外，仿真中载荷随位移上下波动较大，与实际载荷较平稳的现象不符，这是由于仿真中部分单元失效而删除，不再受力使得载荷急速下降，但当接近下一高度处的单元后又再次受力，载荷增大，这种循环造成载荷的波动。

3.3 模型的选择

模型的选择是一个快速发展的多标准决策(MCDM)问题，涉及影响因素众多。基于上述3种仿真模型的精度，选择一种合理的仿真模型是节约时间、控制成本的关键。为解决仿真模型中多组因素误差呈现相互矛盾的问题，作者基于数据敏感的加权损失函数(WLF)[21]，将影响因素的权重转换为数值。在3种模型仿真中，SEA和PCF是最重要的指标，MCF为次重要指标，最后是计算成本(仿真时间)。所有指标均根据其相对重要性进行评分[22]，每次同时比较2个指标(10分)，如果两个指标中的重要性相等，则每个指标各得5分；两个指标最重要的指标得分为8分，次重要指标得分为6分。每两个指标对比完成后，将每个指标的得分相加求和，再除以总分(4个指标比较集数为6，共60分)，得到权重系数，具体如表4所示。为解决仿真误差与仿真时间的数据差异，实现综合评价，将各模型仿真的相对误差与仿真时间映射到[0～1]区间进行无量纲化处理，再乘以加权系数，结果如表5所示。

表4 各指标的评价指标权重系数

表5 经无量纲化及加权处理后各模型的相对误差和仿真时间及综合评价

由表5可以看出：对于多层缠绕管(试样A)，最佳模型为多层连续壳模型，其次是多层常规壳模型，最后是单层壳模型；对于少层缠绕管(试样B)，多层常规壳模型具有最小的误差，其次是多层连续壳模型，最后是单层壳模型。

4 结 论

(1) 采用单层壳模型、多层常规壳模型和多层连续壳模型，基于Hashin失效准则对Al-CFRP混合管的轴向压缩变形过程进行仿真，对于缠绕10层和3层CFRP的混合管，多层壳模型可以更好地反映混合管在准静态轴向压缩下的损伤变形和吸能特性。

(2) 在考虑3种仿真模型的多指标预测误差基础上，添加计算成本的影响因素，综合评估发现：对于多层缠绕混合管，最佳模型为多层连续壳模型，其次是多层常规壳模型，最后是单层壳模型；对于少层缠绕混合管，多层常规壳模型具有最小的误差，其次是多层连续壳模型，最后是单层壳模型。