球墨铸铁断裂韧度测试技术研究进展

郑国华，张欣耀,2，陈 沛，单建军，田庆年

(1.中国船舶重工集团公司第七二五研究所，洛阳 471023；2.河南省船舶及海工装备结构材料技术与应用重点实验室，洛阳 471023)

0 引 言

球墨铸铁具有较高的强度、优异的耐腐蚀性能，并且其生产工艺和设备简单，近年来在轨道交通、风电、核电、南北极开发等领域的高端装备上得到了广泛应用[1-3]。目前，关于球墨铸铁的研究主要集中在硅强化铁素体球墨铸铁[4]、低温高韧性球墨铸铁[5]、城市轨道交通车轮用球墨铸铁[6]、乏燃料运输容器用球墨铸铁等新型球墨铸铁材料的研制和开发上；而在性能方面，除了拉伸、冲击等常规力学性能外，断裂韧性也成为关注的重点。断裂韧度是材料断裂韧性指标，是重要的抗断指标，是工程材料安全服役的关键参量[7-11]；其定义为在弹塑性条件下，裂纹发生失稳扩展的临界状态所对应的应力强度因子(亦即临界应力强度因子)，反映的是材料抵抗裂纹失稳扩展的能力。目前，断裂韧度的测试还是主要基于传统的断裂力学应力强度因子K理论而进行；该方法用于评价传统的高强低韧材料是有效且可行的，但是不适用于新型高韧性的球墨铸铁材料。为了开展高韧性球墨铸铁材料的断裂韧度测试评价，有效指导其工程应用，总结断裂韧度研究进展并提出有效的测试方法就显得尤为重要。为了给广大研究人员提供参考，作者综述了各种断裂韧度测试方法，总结了温度、显微组织和试样尺寸对球墨铸铁断裂韧度的影响规律，探讨了试样裂纹长度测定问题，介绍了基于J-Q(J积分-三轴性应力因子)理论的球墨铸铁断裂韧度测试方法并提出了未来研究的重点。

1 断裂韧度及其测试方法

根据受载方式的不同，断裂韧度分为准静态断裂韧度和动态断裂韧度。准静态断裂韧度根据裂纹尖端应力状态的不同，又分为平面应变断裂韧度(属于线弹性断裂力学范畴)、弹塑性断裂韧度和裂纹尖端张开位移(CTOD)；动态断裂韧度主要是指在冲击载荷作用下的断裂韧度。

1.1 平面应变断裂韧度KIC测试方法

材料发生断裂时，其裂纹形式通常有张开型(I型)、滑开型(II型)和撕开型(III型)3种，其中I型裂纹导致的断裂最危险，破坏也最大，因此在工程上最受关注。在I型加载方式下(外加应力与裂纹面垂直)，有限宽长条板中单边裂纹前端的应力强度因子KⅠ的表达式为

KI=Yσ(πa)1/2

(1)

式中：Y为形状因子；σ为外加应力；a为裂纹半长。

当外加应力σ增大至某一临界值σc，使得裂纹失稳扩展时，这时的临界应力强度因子就叫做材料的断裂韧度，用KIC表示。而如果试样足够厚，属于平面应变状态，则该临界应力强度因子就叫做平面应变断裂韧度。平面应变判定条件为试样厚度B、裂纹半长a和W-a(W为试样宽度)同时大于2.5(K/Rp0.2)2(K为应力强度因子；Rp0.2为屈服强度)。

铁素体只有在足够低的温度(通常为-100 ℃或更低)下才会发生脆性断裂[12]，因此对球墨铸铁而言，只有在足够低的温度下才能满足平面应变条件。此外，除非采用非常厚的试样，否则在高于-40 ℃的温度下也无法测得有效的平面应变断裂韧度。例如GGG-40球墨铸铁，其屈服强度为277 MPa，采用J积分法测得其室温下的平面应变断裂韧度KJIC为102.1 MPa·m1/2,代入式(2)计算可知，其试样厚度至少需为340 mm，才能使用线弹性断裂力学(LEFM)技术获得有效的室温平面应变断裂韧度KIC。

1.2 弹塑性断裂韧度JIC测试方法

随着冶金质量的提高，材料的韧性大幅提升，断裂韧性明显优化。随之而来的问题是，高韧性材料因不能满足平面应变条件，通过断裂韧度试验只能得到条件值KQ，而无法测得有效的平面应变断裂韧度KIC。在这种背景下，选用小尺寸紧凑拉伸(CT)试样或三点弯曲(SEB)试样，在液压伺服疲劳试验机上对试样连续稳定加载，得到一系列不同裂纹扩展长度Δa下的数据点(Δa，J)，通过数据拟合即可得到弹塑性断裂韧度JIC，继而转换成KJIC；这种方法是大多数科研工作者的选择。转换表达式为

KJIC=[EJIC/(1-ν2)]1/2

(2)

式中：KJIC为由JIC转化得到的平面应变断裂韧度；E为弹性模量；ν为泊松比。

随着断裂韧度测试方法和标准的演变和更新，弹塑性断裂韧度JIC计算公式的主体部分没有变化，仍然还包含弹性部分Je和塑性部分Jp；但是Je中的形状因子由g(a0/W)更新为g[(a0+Δa)/W]。此外，测试方法也得到进一步的扩展，由仅能通过施力点位移q来测试，扩展到通过裂纹嘴张开位移V也可以测试。

对于不满足平面应变条件，且能发生裂纹稳定扩展的材料，可选择进行弹塑性断裂韧度JIC测试，以JIC作为其断裂韧性指标，或者进一步通过式(2)将JIC转换成KJIC，从而指导球墨铸铁材料的选材、设计及结构完整性评定。

1.3 CTOD测试方法

一些止裂钢或高韧性材料在断裂时会发生大范围屈服或全面屈服，即断裂前塑性区尺寸已接近或显著超过裂纹尺寸，裂纹发生弹塑性扩展进而在较大应力水平下发生断裂。对于此类材料，通常采用CTOD来评价其断裂韧性。

CTOD测试方法是1963年在英国发展起来的。裂纹尖端张开位移与裂纹长度和外加应力之间的关系如下：

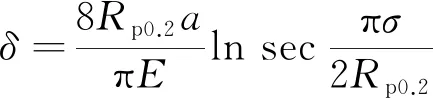
(3)

式中：δ为裂纹尖端张开位移。

当裂纹尖端张开位移达到某一临界值δc时，裂纹发生不稳定扩展导致试样断裂，因此CTOD法把裂纹尖端张开位移作为大范围屈服下裂纹尖端附近应力场和位移场的描述参量，将裂纹开始失稳扩展前的临界张开位移δc作为断裂韧度的指标，作为断裂判据。

1.4 动态断裂韧度KId测试方法

材料动态断裂韧度KId的测试方法并没有像准静态断裂韧度那样完善并已经标准化[13]。国外从20世纪80年代左右就开始了金属材料动态断裂韧度的研究，起初采用的方法各异且测试结果可靠性较差，难以推广使用，近年来逐渐形成了霍普金森压杆(SHPB)加载和示波冲击加载2种较为成熟的试验方法。2015年形成的ISO 26843-2015规范对预裂纹夏比冲击试样动态断裂韧度的测试进行了一般性规定，对动态断裂韧度测试的理论和计算方法进行了论述，但未明确具体的测试程序及实现途径，操作难度较大。我国在20世纪90年代也开始了金属材料动态断裂韧度的研究，迄今为止研究内容主要集中在试验方法、动态断裂韧度的影响因素等方面，尚未形成测试规范或标准。

在工程应用尤其是在风电领域应用时，球墨铸铁结构件经常承受动态载荷(强风引起的振动、受载波动、地震、海啸等)作用，其瞬间应变速率最高可达103s-1，严重威胁着结构的服役安全性。球墨铸铁动态断裂韧度KId通常通过采用夏比V型缺口冲击试样，在其上预制疲劳裂纹后在冲击试验机上进行冲击试验，得到其载荷-时间(F-t)曲线，再进行计算而获得。

2 球墨铸铁断裂韧度的影响因素

球墨铸铁的断裂韧度受温度、显微组织、试样尺寸等因素的影响。

2.1 温 度

球墨铸铁的平面应变断裂韧度和温度之间的关系如图1所示。该关系曲线包含3部分：一个下平台区，断裂韧度不随温度变化，该断裂韧度为最低断裂韧度，也称为下平台断裂韧度KIC-l；一个过渡区，断裂韧度随温度升高而增大，该区域断裂韧度为过渡区断裂韧度KIC-Tr；一个上平台区，断裂韧度不随温度变化，该断裂韧度为最高断裂韧度，也称为上平台断裂韧度KIC-u。图1中的T1为过渡区开始温度，T2为过渡区结束温度。动态断裂韧度和裂纹尖端张开位移基本也满足图1所示规律。

图1 球墨铸铁平面应变断裂韧度与温度的关系Fig.1 Relationship between plane strain fracture toughness andtemperature of ductile cast iron

球墨铸铁的服役温度一般在-400 ℃。纯铁素体球墨铸铁T1T2的温度范围是135.15180.15 K，上平台区和下平台区的平面应变断裂韧度分别为93.75，30.00 MPa·m1/2。珠光体-铁素体球墨铸铁的平面应变断裂韧度随温度的变化规律也如图1所示，随着珠光体含量的增加，上平台区的平面应变断裂韧度从93.75 MPa·m1/2降至65.63 MPa·m1/2。

2.2 显微组织

工程上常用的球墨铸铁通常包含纯铁素体球墨铸铁、铁素体-珠光体球墨铸铁、纯珠光体球墨铸铁3种。纯铁素体球墨铸铁的断裂韧度最高，珠光体-铁素体球墨铸铁的断裂韧度次之，纯珠光体球墨铸铁的断裂韧度最低。

BERDIN等[14]研究了纯铁素体球墨铸铁(A)和含体积分数5%珠光体的铁素体-珠光体球墨铸铁(B)2种材料，这2种球墨铸铁的平均晶粒尺寸均约为30 μm，石墨球直径均接近20 μm，铸铁A和铸铁B中的石墨球体积分数分别为7.7%，10.0%，KIC分别为77，39 MPa·m1/2。铸铁B中的石墨球体积分数较高，石墨球更容易发生聚集，并且裂纹优先从石墨球处萌生并扩展，致使球墨铸铁抵抗裂纹扩展的能力降低，因此断裂韧度更低。此外，该研究[14]还发现，对于同种球墨铸铁，其上平台断裂韧度随着石墨体积分数的增加而降低。事实证明，在保持石墨球数恒定的前提下，很难增加石墨的体积分数。因此，球墨铸铁上平台断裂韧度降低的原因有2种解释，一是石墨球数的增加；二是在保持石墨球数不变的前提下，通过增加石墨球的尺寸而增加其体积分数。

此外，调质处理对球墨铸铁上平台断裂韧度有不利影响[15]；经过调质处理的球墨铸铁形成了大量的珠光体组织，其上平台的断裂韧度仅为50 MPa·m1/2左右，比未经调质处理的球墨铸铁(即纯铁素体球墨铸铁)降低约50%[12]。当其他条件相同时，珠光体组织的形成往往会导致球墨铸铁断裂韧度的降低[16]。英国工程科学数据库(ESDU)资料统计数据[12]显示，和纯铁素体球墨铸铁相比，含体积分数15%珠光体的铁素体-珠光体球墨铸铁的断裂韧度有所降低；随着珠光体含量的增加，铁素体-珠光体球墨铸铁的断裂韧度会持续降低[17]。

2.3 试样尺寸

通常在厚断面金属材料中，不同位置的组织和力学性能差异明显，因此断裂韧度会受到试样厚度的影响。一般球墨铸铁的平面应力断裂韧度KC随其厚度的增加呈递减的趋势，最后趋于一个稳定值，即为其平面应变断裂韧度KIC。因此，对于平面应变断裂韧度KIC，应选取大尺寸试样进行测试，试样厚度B应大于2.5(KQ/Rp0.2)2，需满足平面应变条件。对于弹塑性断裂韧度JIC，应选取小尺寸试样进行测试，试样在到达最大加载载荷之前裂纹不能出现失稳扩展。裂纹尖端张开位移CTOD的测试不受试样尺寸限制。动态断裂韧度KId的测试则受设备吨位的限制，一般选用小尺寸夏比V型缺口冲击试样；随着厚度的增加，动态断裂韧度KId呈递增的趋势，最后趋于一个稳定值。

研究[12]表明，使用三点弯曲试样所测球墨铸铁的断裂韧度一般会偏高。ESDU资料统计了某球墨铸铁单边切口弯曲(SENB)和单边切口拉伸(SENT)试样的断裂韧度，结果表明无论是铸造态还是热处理态，SENB试样的断裂韧度均比SENT试样高20%。因此，当使用由三点弯曲试样获得的断裂韧度数据时，设计者需要考虑测试值偏高的可能性。

3 球墨铸铁断裂韧度测试时裂纹长度测试

对于组织均匀的材料，不论是在预制裂纹后的疲劳加载过程中，还是在准静态加载过程中，试样裂纹前端各个部位始终处于相同的两向应力状态下(表面处于三向应力状态除外)，由于应力的作用裂纹前端各个部位同时产生滑移线，随之形成裂纹并向前扩展。当停止加载时，试样断裂面上会留下裂纹线，其与试样加载线之间的距离即为裂纹长度，可用光学显微镜直接观测得到。但是，由于球墨铸铁的显微组织为铁素体基体上分布着大量的石墨球，在两向应力作用下，铁素体基体和石墨球交界处形成应力集中，裂纹在应力集中处萌生并向前扩展；石墨球的断续分布导致裂纹断续分布，裂纹前端不能形成完整的裂纹线。因此，球墨铸铁中的裂纹长度无法在光学显微镜下观测得到。

根据热处理着色原理[18]，当将金属工件置于氧化气氛中进行热处理时，其表面会生成氧化物，呈现出氧化物的颜色。因此，可将裂纹面在氧化气氛中进行热处理，使其表面发生不同程度的氧化，从而根据颜色来确定裂纹长度。疲劳加载形成的断面和断裂韧度准静态加载形成的断面由于氧化程度不同，产生的氧化物也不同，呈现出的颜色也不同；两种颜色交界处即为裂纹线。这种处理工艺又称为“发蓝”处理。在GB/T 21143-2014中也推荐采用热处理着色工艺来测定裂纹扩展长度，从而得到裂纹长度。由此可见，采用热处理着色方法测定球墨铸铁断裂韧度试样中的裂纹长度在理论上是可行的。但是作者在200～300 ℃下对球墨铸铁中的裂纹面进行热处理后，试样预制疲劳裂纹面和准静态加载裂纹面并没有形成明显的界线，没有观察到完整的裂纹线。而对于这一问题，未见公开文献报道[19]。因此，目前亟需开发出一种有效的热处理着色工艺，以实现球墨铸铁材料断裂韧度试样中裂纹的有效识别。

根据作者实际工作经验和研究，采用350 ℃下保温40 min“发蓝”处理工艺，可有效识别球墨铸铁断裂韧度试样中的裂纹[19]，从而测定得到断裂韧度。

4 基于J-Q理论的断裂韧度测试方法

HUTCHINSON[20]和RICE等[21]给出了Ramberg-Osgood材料在无限大平面问题中的裂纹尖端应力、应变场，计算公式为

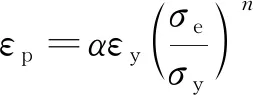
(4)

(5)

(6)

(7)

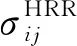
HRR应力奇异场由J积分主导区所控制[22]，因此以HRR应力奇异场为基础的弹塑性J积分理论在韧性材料的断裂分析中得到广泛应用[23]，其中弹塑性断裂韧度JIC是其主要指标。随着球墨铸铁材料韧性的进一步提高，在大范围屈服条件下，有限体浅裂纹试样与拉伸型试样的裂纹尖端场与J积分之间不再具有一一对应的关系[24-26]；即使在JIC测试标准ASTM E1820所要求的试样尺寸得到满足的条件下，JIC值及J阻力曲线仍然依赖于试样几何形状、裂纹深度及试样厚度[27]。进一步的有限元数值分析[28]也表明：平面应变或小范围屈服条件下，不同试样几何裂纹尖端应力-应变场分布特征在给定的J水平下也是不同的。由此可知，单参数的J积分理论已经不适应目前球墨铸铁材料冶金水平的发展，亦即JIC不适用于评估高韧性球墨铸铁材料的断裂韧性。

一些数值分析表明，弹塑性裂纹尖端场明显地受裂纹尖端区拘束的影响。实际上，裂纹尖端场由不同形式的多参数控制[29]。为了描述不同拘束条件下裂纹尖端的弹塑性应力场，O′DOWD等[29]利用有限元方法详细讨论了裂纹尖端应力的变化，提出了描述裂纹尖端应力变化的J-Q[23]理论：

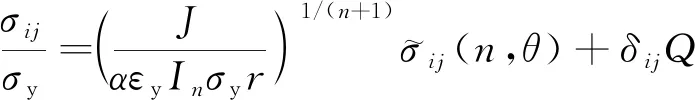
(8)

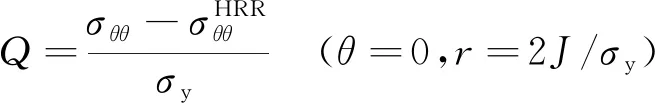
(9)

式中：σij为裂纹尖端应力；δij为裂尖张开位移；r为以裂纹尖端为原点的极径。

J-Q理论虽然较好地描述了裂纹尖端的应力场，但目前国内外大多数研究还是停留在理论模型和有限元数值分析[30-34]阶段，其中核电领域对于J-Q理论的应用研究较多。在基于宏观断裂力学进行结构完整性设计、分析和评定时，需要测定材料的J-Δa裂纹扩展阻力曲线，用以确定结构中延性裂纹扩展的稳定性。但是裂纹尖端区的拘束效应使得J-Δa阻力曲线强烈依赖于试样/结构的几何尺寸和加载方式。如采用现行试验标准ISO 12135-2002(E)和BS 7448-1:1991中的高拘束试样测得的材料断裂韧度和J-Δa阻力曲线评定工程中的低拘束裂纹结构，将得到过于保守的结果[35]。为此，核电领域研究者们建立了拘束相关的材料J-Δa阻力曲线评估方法[36]，实现了实验室试样裂纹尖端拘束和工程结构裂纹尖端拘束水平的较好吻合，显著提高了核电球墨铸铁材料结构完整性分析和评定的准确性。

综上所述，目前的断裂韧度测试都以HRR应力奇异场为理论基础，裂纹尖端的拘束效应对断裂韧度测试结果影响显著[37]。虽然目前现行试验标准推荐的开侧槽措施可以减弱裂纹尖端的拘束效应，但是建立的测试方法本身没有考虑裂纹尖端的拘束。采用实验室高拘束的JIC测试结果评估工程结构低拘束的断裂韧度，会得到过于保守的结果，造成材料大量浪费；通过现行的测试方法和标准确定的损伤容限关键指标KIC存在很多不确定性，致使装备服役时存在安全风险。

5 结束语

此外，目前测试得到的球墨铸铁断裂韧度只是一个通用性的评价，只能给出材料本身的特征参量，仅能用于比较性的选材或简单的断裂力学计算和设计。若要真正用于工程评价和工程安全评定，必须要考虑球墨铸铁的实际加载模式及服役环境。严苛的服役环境会弱化材料的抗断性能，显著增加其服役的安全风险，比如用于轨道交通车辆的球墨铸铁面临着低速加载环境，用于南北极开发设备的球墨铸铁面临着低温、含Cl-海水的腐蚀环境，此外还有设备本身的阴极保护和由此带来的阴极析氢问题等等。因此，球墨铸铁的断裂韧度测试评价应向着真实模拟工程材料及构件的服役环境和加载模式的方向发展。