考虑块石随机空间分布的土石混合体边坡稳定性研究
钱雪晋, 蔡征龙
(1.贵州省水利水电勘测设计研究院有限公司, 贵州 贵阳 550002; 2.三峡大学 水利与环境学院, 湖北 宜昌 443002)
1 研究背景
随着我国西南地区高坝大库的大规模建设,工程中出现了大量的土石混合体边坡[1-2]。由于土石混合体中的土-石物理力学特性的巨大差异,土石接触间复杂的作用关系[3-4],使得土石混合体边坡与传统的均质边坡有着较大的差异,采用传统的边坡安全稳定评价方法来分析土石混合体边坡的稳定性明显不能满足要求[5-10]。
目前,国内外学者针对土石混合体边坡的研究主要是通过试验和数值模拟两个方面进行研究,在数值模拟方面主要是通过各种非均质模型的构建方法来评价土石混合体边坡的稳定性[11-12]。如徐文杰等[13]根据某实际土石混合体边坡的数字图像,结合图像处理方法来模拟相应的土石结构边坡模型,研究了土石结构对边坡稳定性的影响;李亮等[14]结合实际的土石级配比,建立了土石边坡数值模型,分析研究了土石接触的强度参数对边坡稳定性的影响;邵帅等[15]探讨了土石混合体边坡内部不同的块石含量对边坡稳定的影响。上述土石混合体边坡的评价方法仅从确定性评价角度来探讨土石混合体中土-石力学性质的巨大差异对边坡稳定性的影响,但由于坡体内块石含量及空间分布的不同[16-17],导致此类边坡的力学特性及变形特征表现出很强的不确定性[18-19],但鲜有学者考虑这种不确定性对边坡稳定的影响并对土石混合体边坡进行不确定性分析[20]。
为此,本文利用随机块石模型来构建块石随机空间分布的土石混合体边坡模型,根据有限元强度折减法来确定内部随机块石对边坡塑性剪切带的影响,并结合等效强度参数的可靠度法来定量评价土石混合体边坡的稳定性,进而为土石混合体边坡的稳定性评估提供一定参考。
2 模型建立
2.1 随机块石生成模型
由于土石混合体中块石的几何形状多种多样、棱角分明,本文通过对不同直径随机圆的畸变来生成不同尺寸和不同几何形态的随机多边形来模拟内部复杂多变的土石混合体结构。
首先,根据土石混合体内部的级配,用拉丁超立方抽样(latin hypercube sampling, LHS)多维分层抽样法[21],根据块石的实际级配比进行分层设计,将整个累积概率曲线分解成几个区间,每个区间的概率对应不同粒径块石的质量百分比,再向每个粒径区间按均匀分布随机投放块石。
在每个粒径区间内生成不同直径随机圆的方式来生成不同尺寸和不同几何形态的多边形块石,如图1所示。根据相应粒径区间生成以(x0,y0)为圆心,直径为dmax的随机外接圆,并通过畸变系数生成直径为dmin的随机内接圆。
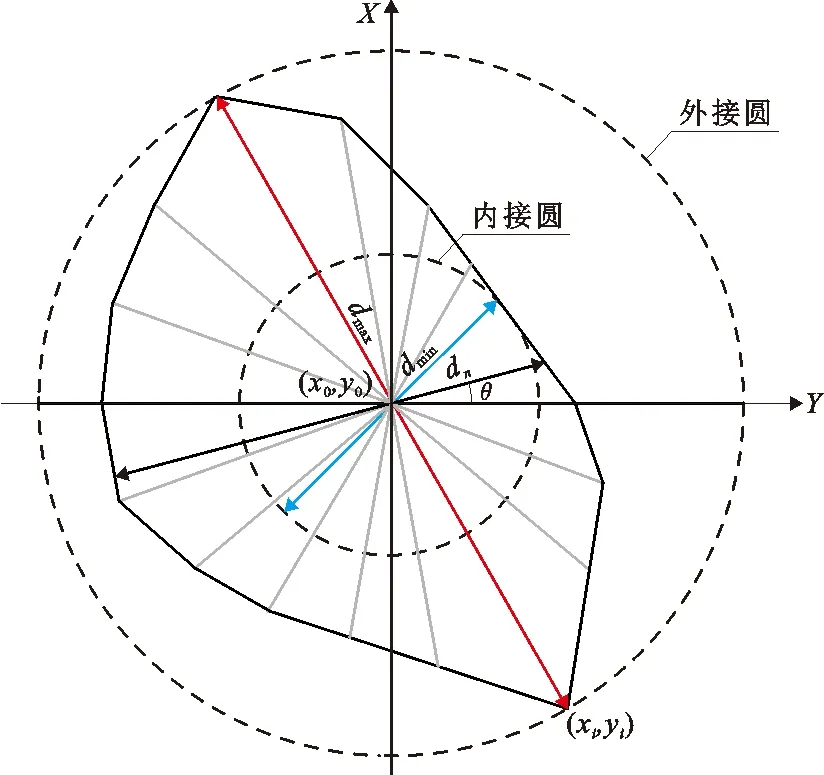
图1 随机块石生成示意图
dmin=(1-μ)dmax
(1)
式中:μ为畸变系数,其取值范围为[0, 0.5]。
以(x0,y0)圆点坐标为基点,将随机圆以圆心等分为n份,每一等分中心角θ=2π/n,结合相应的土石混合体级配,通过调整每等分角度θ的直径dn重构块石的多边形形状特征,直径范围为 [dmin,dmax],相应的多边形顶点坐标可表示为:
dn=dmin+(dmax-dmin)rand(1)
(2)
(x0±0.5dncosθ,y0±0.5dnsinθ)
(3)
式中:rand(1)为随机生成0~1的数。
由于每个块石的顶点都是随机生成,因此必须对计算的随机坐标顶点进行逆时针排序储存。且在随机块石的投放过程中,为避免块石间交叉重叠,必须对块石间进行入侵判断,本文通过计算块石间的圆心到随机圆的直线距离来直接判定块石间是否入侵,极大地简化了入侵判定流程。随机块石模型的生成流程如图2所示。

图2 随机块石模型的生成流程图
定义土石混合体内部块石的含石量m为在一规定区域内大于某一粒径的块石所占体积与该区域总体积的百分比,对于二维土石混合体,其算式如下:
(4)
式中:A和Ai分别为区域总面积和区域内第i个块石所占面积,m2;l为块石总数。
对于任意一多边形块石,能被分解为以圆心(x0,y0)为共同顶点的几个三角形,其中第j个三角形的面积Aj为:
(5)
式中:(x1,y1)和(x2,y2)分别为第j个三角形的其他两个顶点,具体生成流程见图2。
2.2 随机块石模型的构建
本文选取含石量m=15%的土石混合体边坡模型,具体尺寸见图3,其中坡高为10.0 m,左右长度为35.0 m,坡角为45°。

图3 土石边坡计算模型
根据Medley[22]和Lindquist等[23]的研究,土-石区分值dthr为:
dthr=(0.05~0.15)Lc
(6)
式中:Lc为工程特征尺度,m,在本文计算中为坡高,即Lc=10 m。
由公式(6)计算出土-石区分值为0.5 m,大于0.5 m的颗粒为块石,小于0.5 m的颗粒为土,具体级配如表1所示。

表1 土石混合体边坡模型的块石级配
通过上述随机块石方法随机生成含石量为15%的不同空间分布的土石混合体边坡模型,具体模型如图4所示。
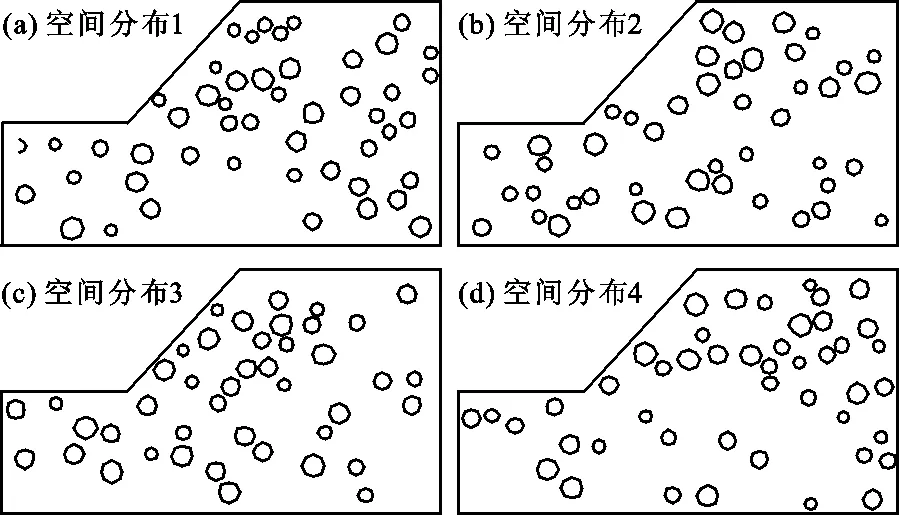
图4 不同空间分布的土石混合体边坡模型(含石量m=15%)
在该算例中仅考虑重力的作用,采用Mohr-Coulomb弹塑性本构模型,土石混合体内部的“土体”与“块石”具体材料参数详见表2。

表2 土石混合体的计算参数
2.3 等效强度参数的边坡可靠度
等效强度参数的边坡可靠度分析方法就是将土石混合体看作一种等效强度参数的均质材料,并通过对非均质材料的力学参数在一定范围区间取值变化来模拟土-石力学参数的巨大差异和块石随机空间分布对土石混合体稳定的影响。土石混合体边坡稳定的功能函数为:
Z=g(X)=Fs(X)-1
(7)
式中:Fs(X)为随机变量X条件下的安全系数,且X相互独立,服从正态分布,采用二次多项响应面法来描述边坡稳定的功能函数,具体表达形式为:
(8)
式中:a、bi、ci均为拟合系数。
可靠度分析的基本步骤具体如下:
(1)设置初始设计点X(1)=X1(1),…,Xi(1),…,Xn(1),一般为随机变量的均值。
(2)利用中心复合设计,构建2n+1个功能函数:Z=g(X1(1),…,Xi(1),…,Xn(1))、Z=g(X1(1),…,Xi(1)±fσi,…,Xn(1))。其中f在初始试算中取3,之后为1。
(3)结合公式(8)和功能函数计算相应的拟合系数值。
(4)根据一次二阶矩法[24]计算验算点X*(k)和可靠度指标β(k)。
(5) 根据|β(k)-β(k+1)|<ε收敛法则,如满足则停止迭代计算,否则通过公式(9)进行插值,并重新返回到步骤(2)进行计算,直至满足收敛条件。
(9)
3 结果与分析
3.1 基于随机块石的边坡稳定性
由于有限元强度折减法无需预先确定边坡的滑动面,这里采用有限元强度折减法对上述不同空间分布模型的土石混合体边坡的稳定性进行计算分析。图5和6分别为含石量m=0条件下的均质边坡和含石量m=15%不同空间分布的土石混合体的边坡塑性剪切带。由图5和6可以看出,由于边坡内部的“土”与“石”力学性质的巨大差异,剪切带表现出了明显的“欺软怕硬”特性,会发生如图7所示的明显“绕石”“分流”现象,同时由于坡体内部块石空间分布的随机特性,相同含石量条件下生成的随机块石模型也有所不同,导致不同空间分布条件下,土石混合体内部的剪切塑性变形也会有所不同。

图5 均质边坡的塑性剪切带分布(含石量m=0)

图6 不同空间分布的土石混合体边坡塑性剪切带分布(含石量m=15%)

图7 剪切带的“绕石”“分流”现象示意图
由图6还可看出,15%含石量的土石混合体边坡为随机空间分布时,坡体内的塑性剪切带区域也表现出明显的区别,对塑性剪切带的“阻挡”作用明显不同;当坡体内块石较多地出现在剪切带时,如图6(a)、6(b)和6(c)所示,塑性区域则会因块石的“绕石”“分流”现象表现出多条塑性剪切带,可见由于块石阻挡了塑性剪切带的扩展趋势,边坡的稳定性得到明显的提高,计算的安全系数分别为1.22、1.18和1.27,明显高于均质边坡的安全系数1.10。当块石未出现在均质边坡的剪切带时,如图6(d)所示,其塑性区域与均质边坡的塑性区域基本一致,表明该空间分布对此边坡稳定性影响很小,计算的安全系数为1.12也与均质边坡的安全系数较为一致。
综合上述结果,基于随机块石模型虽能直观反映内部块石的不同空间分布对土石混合体边坡稳定性的影响,但不同随机块石生成的边坡模型计算的安全系数均有所不同,多个不同的安全系数导致难以直接定量评价土石混合体边坡这种非均匀性边坡的稳定性。
3.2 土石混合体边坡的可靠度
由于块石的空间分布不同,随机块石模型计算的边坡安全系数也会有所差异,因此在对土石混合体边坡的稳定性进行可靠度分析时,必须充分考虑这种随机性。随机块石模型每次生成的边坡模型均具有一定的随机性,仅能通过蒙特卡洛法对其进行边坡稳定的可靠度分析,这就需要建立大数量级的随机块石边坡模型并进行有限元的确定性分析,极大地限制了其在边坡可靠度分析上的应用。
为了避免大数量级的边坡模型重构,在边坡稳定的可靠度分析中,本文采用等效强度的方法将土石混合体看作一种等效强度的均质材料,结合文献[25]土石混合体的相关试验成果,不同含石量条件下土石混合体的摩擦角φbim和黏聚力cbim可用公式(10)~(12)进行求解:
(10)
(11)
(12)
式中:m为含石量,%;φmatrix为土体的摩擦角,(°);UCSmatrix为土体的单轴抗压强度,kPa;UCSbim为土石混合体的抗压强度,kPa;A为拟合参数,取值为0.1~500;a为休止角,取值为30°~45°[26]。
在本文中UCSmatrix取值为44.5 kPa,结合公式(10)~(12)得到不同参数条件下土石混合体等效强度参数的黏聚力和摩擦角的取值范围,具体如图8所示。由图8可以清晰地看出,休止角a的大小决定了土石混合体的摩擦角值(图8(a)),而拟合参数A影响着黏聚力(图8(b))。休止角和拟合参数的不确定性决定了土石混合体的抗剪强度参数不是一个确定值而是一个范围区间。

图8 土石混合体等效强度参数的黏聚力和摩擦角的取值范围
本文得出剪切强度参数黏聚力和摩擦角的均值分别为14.88和22.06,标准差分别为0.97和0.44,假定抗剪强度参数黏聚力和摩擦角均服从标准正态分布,再结合2.3节的等效强度可靠度分析法进行边坡稳定性分析,计算得到相应的可靠度指标为2.433,对应的失效概率为0.075。
综上所述,相比于随机块石边坡模型,等效强度参数模型通过抗剪强度参数区间范围的取值来量化土-石力学参数的巨大差异和块石随机空间分布的影响,虽不能反映内部块石对边坡剪切带的影响,但能通过一个确定值直观、定量地评价土石混合体的非均匀性对边坡稳定性的影响。
4 结 论
本文从随机块石模型和等效强度参数的可靠度模型两个角度来综合研究分析块石的随机空间分布对边坡稳定的影响,为土石混合体这类边坡的稳定性设计提供参考依据。主要结论如下:
(1)土石混合体内部的块石对边坡剪切带的扩展起到了明显的“阻隔”作用,其圆弧型的塑性剪切带由于块石的含量和分布的不同,出现不同的“绕石”“分流”现象,易生成多条塑性剪切带,且块石空间分布的不同,塑性剪切带也会有所差别。
(2)随机块石的边坡模型能很好地展现内部块石的随机空间分布对边坡稳定性的影响,即当块石处于剪切带时,能显著提高边坡稳定性,但大数量级的模型重构和有限元分析极大地限制了其在边坡可靠度分析上的应用。
(3)基于等效强度参数的边坡可靠度方法无需对边坡模型进行重构,极大地节省了计算工作量,但该方法无法直观地反映出内部块石如何影响边坡的稳定性,且如何准确地通过抗剪强度参数的取值范围来量化随机块石对边坡稳定性的影响,这仍值得进一步探讨。

