融冰洪水演进的马斯京根模型
林 瑜, 吕海深,2, 朱永华,2, 孙铭悦, 张梅洁
(1.河海大学 水文水资源学院, 江苏 南京 210098; 2.河海大学 水文水资源与水利工程科学国家重点实验室, 江苏 南京 210098)
1 研究背景
在我国高纬度地区的河流,如黄河宁蒙河段、新疆阿勒泰等地区的河段,河道内的水流会随着气温的下降不断凝结成冰,解冻开河时期,河道冰盖在热力、动力等因素的综合作用下又逐渐消融,槽蓄水量沿程释放,加上上游的来水和来冰而形成凌汛。在冰凌洪水演进的过程中,河道的急弯、窄口等位置容易发生冰凌堆积,从而抬高水位,严重时会发生漫滩决堤,造成冰凌灾害[1]。因此,准确的凌汛预报有利于防汛部门在洪水发生前及时转移人员及公共财物,以降低灾害造成的损失,对防凌减灾及水资源的合理利用具有一定的现实意义。
近年来,国内外学者对于冰凌问题展开了深入的研究。由于经验性和统计性的方法在河流冰情预报方面的成功率较低,因而无法在众多河流上得到广泛应用,它们往往仅用于预测河流冰情可能产生的结果。针对以上两种方法的不足,许多学者采用了更为先进的方法来改进对河道解冻日期和流量的预测,如k近邻算法[2]、决策树模型[3]、神经网络[4]和模糊逻辑模型[5]。这些模型中有许多是通过将信息汇集到一个由连接节点组成的结构循环中,将一系列输入信息(如水文、水力和气象变量)与特定的结果(如解冻日期和洪水水位)联系起来的,并在这个结构中对信息进行决策(例如流量是否超过某个阈值),输出对河流冰情的可能性预测。但这些方法中没有描述输入与结果之间因果关系的物理过程,这种因果关系需要利用河冰生消演变的确定性模型进行模拟,如River2D模型[6]和HEC-RAS模型[7]。2017年,Lindenschmidt[8]提出RIVICE模型,模拟了河冰形成的关键过程,如冰的产生、冰的运输、冰盖的发展和冰塞的形成,该模型已成功应用于加拿大的一些河流中。我国黄河冰凌问题的研究仍处于一个探索和发展的阶段,在相关科学和技术方面还有很大的提高空间[9]。 2012年,黄河水利委员会水文局开发了冰凌预报系统,该系统将经验与理论的方法相结合,提高了冰凌预报精度[10-11];杨开林[12]对冰盖河渠在恒定流条件下的水深平均流速的横向分布展开了研究,提出了一种准二维模型;张防修等[13]为确定凌汛期槽蓄水增量来源及其形成过程,忽略融雪水量等影响因素,建立了河冰水动力学模型。
利用河冰水动力学模型进行冰凌洪水预报,需要大量的数据,如糙率、断面资料等,而且河冰堆的存在更是加大了河冰水动力学问题的难度和复杂性。因此,针对该问题,有学者将马斯京根法应用到冰凌洪水预报中。在流量相同的情况下,冰盖的存在使得河流的水位高于明流条件下的水位[14],同时,含冰盖的河段蓄水量大于明流的蓄水量。因此,传统的马斯京根模型不适用于河冰消融时期的洪水演算。2018年,王恺祯等[15]尝试将马斯京根模型应用于冰期洪水计算中,建立了考虑河道冰期有冰凌存在情况下的马斯京根模型,并以黄河宁蒙河段为研究对象,通过验证马斯京根模型参数的可靠性,得出了采用马斯京根模型进行河道冰期洪水演算可行的结论。2019年,Yang等[16]通过对河冰消融时期洪水演进的研究,将冰盖融化所释放的水量视为入流量,对传统的马斯京根模型进行了改进,以演算河冰解冻时下断面的出流量。该方法所模拟的结果与实测出流吻合良好。
通过优化算法率定的参数,其实际参数的特性可能会不同于传统的马斯京根模型,因此该模型应改用试错法率定参数。但采用试错法确定参数α(冰盖融化过程中产生的入流量与上游河段的入流量之比)和x(流量比重因子)时,试算过程比传统马斯京根模型更为复杂和困难。针对这一问题,本文试将演算河段内的融冰量视为演算下断面出流量的一部分,拟提出一种适用于河冰消融时期的融冰洪水演进的马斯京根模型,并采用传统的试错法、非线性规划法和智能算法中的遗传算法率定模型参数,进而对比各方法的模拟效果和精度。
2 马斯京根模型的基本原理
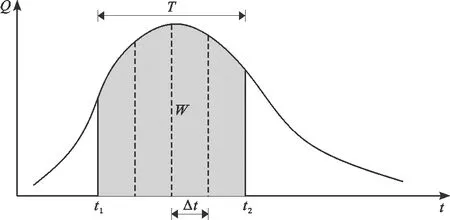
马斯京根模型(Muskingum routing model)由麦卡锡(G.T.Macarthy)于1938年提出,该模型建立在圣维南方程组的基础上并进行简化计算,分别用河段水量平衡方程和河道槽蓄方程简化连续性方程和复杂的水动力方程,被广泛地运用于河道洪水演算中。河段水量平衡如图1所示,其基本方程为:
dW/dt=I-Q
(1)
W=KQ′=K[xI+(1-x)Q]
(2)
式中:W为河段的槽蓄量,m3;I、Q分别为河段上断面的入流量、下断面的出流量,m3/s;t为时间,s;Q′为示储流量,m3/s;K为槽蓄系数,s;x为流量比重因子。
假定河段流量在计算时间内呈线性变化,则公式(1)、(2)的有限差分解为:
(3)
(4)
C0+C1+C2=1
(5)
参数K为槽蓄系数,表示当水流处于恒定流状态时,相应槽蓄量下的河段传播时间。参数K值一般需根据洪水通过河段的传播时间来估计。参数x为流量比重因子,即运动中扩散波洪峰衰减和洪水传播过程坦化的物理参数,是反映河槽调节作用的指标之一。在马斯京根模型中,引入参数x使某个范围的槽蓄量与其下游的出流量具有单值关系,同时特征河长的河道蓄水量与下游段出流量绝对具有单值关系。因此,两者具有一定内在联系,其关系式为:
(6)
式中:x1为楔蓄的大小,是表示水面曲线形状的参数;L为河段长,m;l为特征河长,m。
若水面为直线,则有:
(7)
(8)
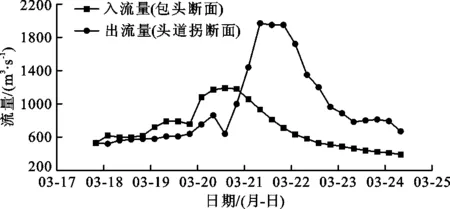
根据公式(8)可知,当x=0时,L=l;当0 显然,马斯京根模型应用的一个关键性问题在于模型参数K、x值的估计。传统优选方法诸如试错法、最小二乘法等,这些方法均基于对马斯京根法中W(河段的槽蓄量)-Q′(示储流量)关系形式作单值线性的假设来选择参数K、x的最优值。只要确定了K、x值及演算时段t,根据公式(4)可求出C0、C1、C2,再使用公式(3)进行流量演算。 冰期与明流条件下的河道流量组成相比,增加了消冰水量等[17],造成河段下游出流量过程线的峰值远高于上游入流量过程线的峰值。因此河冰消融时期的洪水演进与明流条件有所不同。 在河冰消融期,仅考虑在文开河及热力作用的条件下,将河段内的融冰产生的流量视为河段下断面出流的一部分,用Om表示。河段径流量计算如图2所示。 图2 河冰消融期河段径流量计算图 根据图2,T时段内的径流量W计算公式为: (9) 式中:Q(t)为某一时刻的流量,m3/s;t1、t2为时段T初始和终止的时刻。 (10) 此时径流深R为: (11) 式中:W为T时段内的径流量,m3;F为流域面积,km2。 利用上述计算流量的方式推求河段内的融冰产生的流量Om。 Bilello[18]通过累积正气温对最大冰厚值进行修正,提出了一种模拟冰盖消融过程的计算方法,其计算公式为: hj=hmax-ASt (12) 式中:hmax为冰盖开始融化前最大厚度,m;St为累积解冻度日,℃·d;A为经验系数,可利用多年实测冰厚值求得A值,m/(℃·d)。 根据公式(12)可计算冰盖消融的厚度,因此河道内因融冰所产生的径流量W: W=1000Δh·F (13) 式中: Δh为计算T时段内的冰盖消融厚度,mm;F为河道冰盖的面积,km2。 (14) 因此下断面的出流O由两部分组成:一部分为因上断面的入流量在下断面处产生的出流量,用Ow表示;另一部分为演算河段内因冰盖消融在下断面处产生的出流Om。即: O=Ow+Om (15) 若仅考虑上断面入流量在下断面处产生的出流量时的马斯京根方程为: (16) 假定流量在河段和计算时间内呈线性变化,求解同传统的马斯京根模型相同,则公式(16)的有限差分解为: (17) (18) C1+C2+C3=1 (19) 因此,河段下断面的出流量计算公式为: (20) 解冻开河时期,随着河道槽蓄量的逐段释放,洪峰不断向下游推进且增大,形成凌峰。此时,融冰对下游出流量的影响较大,所以应根据下断面出流量的变化情况对模型参数进行分段率定。 流量比重因子x是反映洪水传播过程坦化及洪峰衰减的物理参数,x值越大,出流过程线的坦化程度越弱。当河冰开始融化,槽蓄水量沿程增量释放,导致下游出流量过程线峰型呈尖窄状,且峰值远高于上游入流量过程线的峰值。故0 采用试错法计算融冰洪水演进的马斯京根模型,参数K、x计算及流量演算的步骤如下: (1)根据洪水和河段的资料情况,对计算时段Δt进行选取; (2)根据演算河段的气温资料,计算河段内因冰盖消融在下断面处产生的出流Om,进而计算Ow。同时根据下断面出流量的变化情况划分模拟时段,分为受融冰影响较小和较大以及无冰3种时段。 (3)根据河段的入流量Iwi和Owi计算Wwi; (4)假定x计算示储流量Qw,其关系式为: Qw=xIw+(1-x)Qw (21) (5)点绘Ww-Qw关系,寻找某一值使得Ww-Qw最能成为单一线性关系,从而计算K。 (6)将步骤(5)所确定的参数K、x的最佳值及计算时段Δt代入公式(18)计算C1、C2、C3; (7)由河段的入流量Ii、第1个演算时段的Ow,根据公式(17)和(20)逐时段对出流过程Qi进行演算。 黄河宁蒙河段干流纬度为37°15′~40°51′N,位于黄河流域最北端。该河段起于黑山峡水位站,止于头道拐水文站,水流自低纬度流向高纬度。由于纬度的差别,导致11月至次年2月期间低纬度河段的多年平均气温高于高纬度河段,使得该河段自下游向上游封冻,而开河的方向却与之相反。因其地理位置特殊,该河段具有显著的大陆性气候特征,同时受河道边界条件的影响,造成该河段凌情最为严重且频繁[19]。 近年来,黄河宁蒙河段凌汛灾害的影响因素有气候、水文情势、人类活动等,随着这些影响因素的变化,凌汛灾害不断呈现新的变化趋势[20]。在全球气候变暖的趋势下,最大冰厚整体上逐年变薄,冰厚自上游至下游沿程增大。凌汛期,由于气温升降交替或剧变,该河段多封多开、封开河交替现象日益频繁。流量小水位高的特点突出,但两者非同步变化。与此同时,凌峰流量增大且自上游至下游呈递增趋势。凌汛致灾机理的复杂化大大提高了凌汛风险调度和防控的难度。因此高精度的洪水演算成果是凌汛防控的重要依据之一。 本文选取宁蒙河段中的包头至头道拐这一河段作为融冰洪水演算河段,如图3所示。该河段全长150 km,平均河道宽度为660 m。2015年11月25日,河段内有初冰生成,至12月中旬,河流进入封冻状态,河段内最大冰厚为0.58 m。2016年3月15日前后,河流开始解冻,7日后终冰。根据河段洪水和冰情资料,演算时间选取2016年3月18日至3月24日,Δt选取6 h。河段的实测入流量与出流量如图4所示。 图3 黄河宁蒙河段(石嘴山-头道拐段) 由图4可知,受河冰消融的影响,头道拐断面处的流量峰值远高于包头断面处的流量峰值,且出流量过程线呈现“尖瘦”型峰值。入流量与出流量洪峰滞后的时间相对较短,所以冰盖在热力、动力等作用下消融速度快,从而使得洪波速度加快。 图4 黄河包头-头道拐河段实测洪水过程线(2016-03-18-03-24) 根据三湖河口、包头和头道拐的多年冰情资料及周围气象站气温数据,可得经验系数A=0.003 17 m/(℃·d)。该实例假定包头至头道拐河段内的河冰以河道平均宽度均匀分布,且不考虑上游入流的冰量。模型所模拟的河段终冰日期为2016年3月22日,与河段实际终冰日期相符合。采用试错法分别对融冰洪水演进的马斯京根模型和传统的马斯京根模型的参数进行率定,演算成果如图5所示。 由图5可知,将传统的马斯京根法应用于河冰消融时期,模拟效果较差,其模拟洪水峰值远低于实测出流过程线的峰值,而改进后的马斯京根模型模拟的出流过程线与实测出流过程线吻合良好,精度高于传统的马斯京根模型。进一步说明了传统的马斯京根法需加以改进,才能更好地应用到冰期洪水演算中。 采用试错法、非线性规划法和遗传算法率定的各模拟时段的参数值见表1。非线性规划法和遗传算法演算出流过程线如图6所示。 图6 实例河段非线性规划法与遗传算法演算的出流过程线对比 采用确定性系数Dc与过程平均相对误差RE作为精度评价指标,以评定各方法对河段出流量模拟结果的可靠性和有效性。当Dc越大、RE越小时,说明该方法模拟结果的可靠性和有效性越高。合格判别标准为:确定性系数Dc<0.7,且过程平均相对误差RE<20%[21]。 确定性系数Dc的计算公式如下: Dc=1-Sc/Sy (22) (23) (24) 过程平均相对误差RE的计算公式如下: (25) 各方法对河段出流量模拟精度的评价指标计算结果如表2所示。 表2 各方法对河段出流量模拟精度的评价指标计算结果 由表2可知,各算法在各时段以及整体上模拟结果均合格。从整体上看,非线性规划法模拟本次洪水的精度最高,试错法精度最低。但在受融冰影响较大的情况下,试错法所模拟的精度最高,并且由图5可以看出,试错法模拟的洪峰流量更接近实测值。对比冰期与无冰期洪水演算精度,该模型对冰期洪水演算精度较高,因此所构建融冰洪水演进的马斯京根模型是可行的。 对比试错法、非线性规划法和遗传算法3种方法所率定的参数,在受融冰影响较小时段,3种方法率定参数值差异最大。流量比重因子x受水面曲线形状参数x1的影响,若水面为直线,则x1取值为0.5,由于河冰的存在改变了明流的状态,由此可能对x的范围产生一定的影响,甚至出现负值。在使用试错法率定无冰情况下的参数时,参数率定范围与传统马斯京根一致,使其率定值与其他两种方法差异较大。因此,对于河冰消融时期的马斯京根模型参数的范围有待进一步研究。 在所构建的模型中,因冰盖消融而影响下断面处出流量的因素有3方面:(1)由于现阶段计算冰体积的手段和方法有限,因此,基于河冰以河道平均宽度均匀分布的假设估算河段内贮存的冰量与实际存在一定的误差;(2)模型仅考虑热力作用下的河冰消融,忽略风、太阳辐射、动力和河势等因素对河冰融化影响;(3)模型将融冰产生的平均流量视为下断面出流量,未考虑融冰所产生的流量在传播过程中的时滞。因此,该模型具有一定的局限性,还需进一步改进以扩大其应用范围。 (1)模型预测的无冰日期为2016年3月22日,与实际相符,说明了在河冰解冻消融时期,在文开河及仅考虑热力作用下冰盖融化的情况下,使用Bilello提出的度日因子法计算冰厚,及模型应用实例中对冰分布的假设具有一定的可行性。 (2)采用传统的试错法、非线性规划法和智能算法中的遗传算法分别率定模型参数K、x,各算法无论在各时段还是在整体上的演算结果均合格,演算出流过程线与实测出流过程线较为吻合,演算精度高且降低了参数率定的复杂性。 (3)相比较而言,非线性规划法演算精度略高于遗传算法,其对河段出流洪水的整体确定性系数Dc的计算结果为0.980,洪水出流过程线的平均相对误差RE为4.840%;试错法的演算精度最低,但试错法模拟的洪峰流量与实测洪峰流量的误差最小。 (4)所构建的融冰洪水演进的马斯京根模型模拟精度较高,为融冰洪水演进的研究提供了一种新方法,但还存在一些局限性。为扩大模型应用范围以及实用性,还需结合更多科学方法与技术手段对融冰时期的参数范围和因冰盖消融而在下断面处产生的出流量进行深入的研究。3 融冰洪水演进的马斯京根模型建立
4 模型应用实例

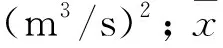

5 讨 论
6 结 论

