基于小波变换的长江中下游地区极端降水与大气环流响应关系研究

吴舒祺， 赵文吉， 杨 阳， 金囝囡， 郑冬阳， 王欣玉

(1.首都师范大学 资源环境与旅游学院， 北京 100048； 2.首都师范大学三维信息获取与应用教育部重点实验室，北京 100048)

1 研究背景

在全球变暖背景下，全球水文循环加速，全球范围内极端降水事件的频率增加，对农业、基础设施以及生态环境造成重大破坏。我国也极易遭受极端降水等自然灾害(如洪水)的影响[1]。例如1998年长江流域大洪水、2010年的东北季节性洪灾以及2012年北京特大降水，均造成了巨大的经济损失及人员伤亡[2-4]。极端降水的变化呈现出复杂的模式并且具有明显的区域特征，例如德国大部分地区极端降水具有增加趋势，但是非洲南部和西部的极端降水变化不明显，位于中美洲的加勒比地区极端降水指数在1985-2015年变化不显著[5-6]。对于中国而言，极端降水事件也表现出明显的空间差异。在长江流域、西南和华南地区的极端降水具有年代际增强趋势，东北地区则表现出减弱趋势[7-8]。在区域及地方尺度上研究极端降水变化模式特征对于国家应对全球气候变化是极其重要的。相关研究中指出，中国极端降水增加趋势显著的区域主要集中在长江中下游地区[9-10]。作为我国重要的经济区，该地区洪涝灾害频发，极端降水是主要原因之一[11]。

作为极端降水变化的遥相关因子，大气环流(厄尔尼诺、北极涛动、北大西洋涛动等)通过影响雨带移动和水汽输送作用来改变区域水文要素[12]。探讨大气环流因子对极端降水的作用机制，可以为地区洪涝灾害防护以及科学管理提供重要的理论依据和数据支撑。前人的研究主要注重趋势研究或者变量之间的线性关系研究，对于各变量的周期变化以及相关显著周期的研究不多[13-17]。极端降水对大气环流变化的响应往往是不对称的，并且通常不能描述为线性行为[18]。标准复合分析方法或相关分析等不能区分不同时间尺度的变化，也无法适应非单调和非线性关系。为了分析这些大气环流因子对极端降水的影响，必须考虑它们之间的非线性行为和多尺度效应[19]。最近的许多研究，尤其是Torrence等[20]和Nalley等[21]进行的研究工作证明了基于小波变换的频谱分析方法是分析水文气候变量中多尺度关系的有力工具[20-21]。揭示大气环流与区域极端降水变化之间的各种耦合振荡行为，尤其是它们的时域分布特征显得尤为重要。

基于此，本文采用连续小波变换的方法对长江中下游地区的极端降水指标的周期变化以及相关显著周期进行研究。为了量化不同时间尺度上两个水文气候变量之间的关系，本文使用了基于连续小波变换的交叉小波变换(cross wavelet transform, XWT)及小波相干(wavelet coherence, WTC)，根据交叉小波功率谱、交叉小波凝聚谱和相位差，分析了二者在时频域中的多时间尺度相关关系及其所包含的周期特征，从时间尺度上探讨了长江中下游地区极端降水与大气环流因子的响应关系，以期为区域防灾减灾以及农业生产提供相关的科学依据，促进当地社会经济与生态系统和谐发展。

2 数据来源与研究方法

2.1 研究区概况

研究区长江中下游地区(106°54′E～124°25′E，24°30′N～35°45′N)包括：湖北、湖南、江西、安徽、江苏、浙江以及上海等省(市)，其概况如图1所示。研究区中部地区和沿江沿海地区高程较低(图1(a))，多年(1980-2018年)平均气温为16.81 ℃，多年(1980-2018年)平均降水量为1 356.66 mm(图1(c))，春夏季节降水较多，并且降水分布不均。长江中下游地区是中国主要的粮食生产基地，人口密集、社会发展程度高，极端降水事件作为该地区洪涝灾害频发的主要原因之一，值得进行深入研究[22]。

2.2 数据来源

本文所采用的降水资料来源于国家气象信息中心，包括浙江、江苏、上海、安徽、湖南、湖北等7省(市)1980-2018年489个地面监测站点的逐日降水量资料，由于1980年前该地区数据缺失严重，本研究选取的时间段为1980-2018年。剔除降水年份缺失严重的站点数据，最后保留435个地面监测站点。在检查数据的可用性之后，使用RClimDex进行质量控制， 并使用基于惩罚最大T检验(penalty maximumttest, PMT)和惩罚最大F检验(penalty maximumFtest, PMFT)的RHtests_dlyPrcp对降水时间序列的均一性进行检验[23-25]。本研究所采用的大气环流指数为：东亚夏季风(East Asian Summer Monsoon, EASM: http://ljp.gcess.cn/dct/page/1);厄尔尼诺-南方涛动(El Nio-Southern Oscillation, ENSO: http://www.cpc.ncep.noaa.gov/)，北极涛动(Atlantic Oscillation, AO: http://www.cpc.ncep.noaa.gov/)，北大西洋涛动(North Atlantic Oscillation, NAO: http://ljp.gcess.cn/dct/page/1)，太平洋涛动(Pacific Decadal Oscillation, PDO: http://www.esrl.noaa.gov/psd/data/correlation/pdo.data)；印度洋偶极子(Indian Ocean Dipole, IOD: http://www.jamstec.go.jp/frsgc/research/d1/iod/index.html)

2.3 极端降水指数

本文利用百分位阈值法定义极端降水事件,选用两种不同的百分位阈值，即以95%和99%分位数作为极端降水分析的阈值(表1)。

根据每个站点日降水量大于0.1 mm的按升序排列的第95%和99%的降水量值作为该站点极端降水量的阈值。极端降水天数指的是1年中日降水量超过该降水阈值的天数。

2.4 研究方法

2.4.1 连续小波分析 本研究选择Morlet小波分析方法进行气候要素的周期变化研究。

Ψ(t)=π-1/4eiω0te-t2/2

(1)

式中：Ψ(t)为基小波函数;i为虚数； e为自然数；t为时间；ω0为无量纲频率。

对于给定的时间序列和Morlet小波,其小波变换为：

(2)

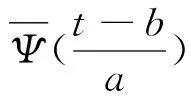
(3)

由小波变换方程得到的不同时间尺度的所有小波系数在b域上积分，就可得到小波方差：

(4)

2.4.2 交叉小波变换及小波相干 Torrence和Compo引入了交叉小波和小波相干，以研究时频空间中两个时间序列之间的关系。两个时间序列xn和yn的交叉小波(XWT)定义为：

Wnxy=WnxWny*

(5)

式中：Wny*为复共轭。交叉小波功率谱密度可以定义为|Wxy|。XWT能够反映时频空间中两个时间序列具有的相同较高能量谱区域，从而揭示两序列在不同时域上相互作用的显著性。小波相干可以反映时频空间中两个序列的协方差强度，更侧重两时间序列在低能量区的相关性。小波相干性定义为：

(6)

式中：S为平滑算子。值得注意的是，该定义与传统的相关系数十分相似，可以将小波相干视为时频空间中的局部相关系数。

本文运用红色噪音标准谱对交叉小波功率谱和小波相干谱进行显著性检验。相关方法和参数的更多详细说明，请参考文献[20]。

3 结果与分析

3.1 极端降水指数周期特征

XWT用于确定极端降水指标的周期性变化，各个极端降水指标的小波变换及小波方差如图2所示。图2中的红色实线以及红色虚线表示置信度为95%的红噪声检验，黑色弧形虚线为小波影响锥。影响锥表明，部分小波功率谱受边缘效应的影响，周期性特征存在较大的不确定性。一般来说，尺度越长，边缘效应影响越大。

研究期内，长江中下游地区极端降水指数存在不同时间尺度的年际振荡(图2)。R95p的第一主周期为3.47 a，在1980-1987年间具有3～4 a的显著周期，此后在1990-2005年间具有2～4 a的显著周期，并且振荡幅度较大；在2005-2012年间具有2～3 a的显著周期(图2(a))。R95d的第一主周期为2.25 a，第二主周期为3.47 a，在1985-1990年间具有2～4 a的显著周期，在1990-2005年间具有2～4 a的显著周期，此后的2005-2012年间具有2～3 a的显著周期(图2(b))。R99p的第一主周期为3.79 a，在1984-1987年具有3～4 a的显著周期，1992-2012年具有2～4 a的显著周期(图2(c))。R99d在研究期内的显著周期变化与R99p大致相似，并且与R99p均以3.79 a为第一主周期，但是在时域中，能量强度部分并不完全相同，存在明显的局部化特征(图2(d))。

3.2 大气环流指数周期特征

大气环流指数连续小波变换及小波方差如图3所示。由图3可看出，EASM的第一主周期为2.92 a，在1985-2005年间具有2～5 a的显著周期，在2005-2012年间具有2～3 a的显著周期(图3(a))。ENSO以3.79 a为第一主周期，5.36 a为第二主周期，在1984-2005年间具有2～7 a的显著周期，在2007-2012年间具有2～3 a的显著周期(图3(b))。

AO以4.13 a为第一主周期，在1985-1996年间具有3～6 a的显著周期，在1992-1996年间还叠加着2～3 a的显著周期，此后的2002-2012年间具有2～6 a的显著周期(图3(c))。NAO以2.25 a为第一主周期，以3.47 a为第二主周期，在1985-1990年间具有2～4 a的显著周期，在1990-1998年间具有2～3 a的显著周期，在2003-2012年间具有2～4 a的显著周期(图3(d))。相对而言，PDO表现出的周期信号较弱，PDO以5.36 a为第一主周期，在1988-1998年间具有4～6 a的显著周期，1998-2004年间具有9～10 a的显著周期，但是此后的显著周期受到小波边缘效应的影响(图3(e))。IOD的第一主周期为2.92 a，其在1985-2012年间具有2～4 a的显著周期(图3(f))。

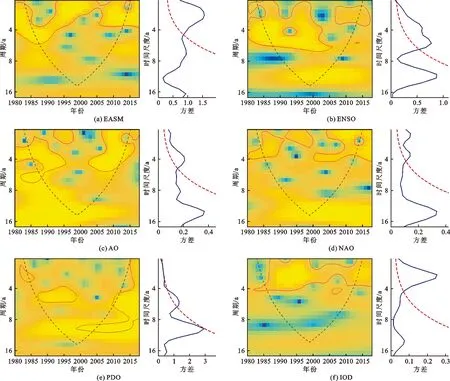
图3 大气环流指数连续小波变换及小波方差

以上结果表明，长江中下游地区极端降水指数与大尺度大气环流因子在一定时间上存在着相似的周期变化，但两个变量之间周期的相似性没有经过统计检验，是否仅是一种巧合还需要验证。连续小波变换只是针对单个因子单独进行时频变化模式分析。因此，需要采用交叉小波变换进一步分析它们之间的共同信号[26]。

3.3 大气环流对极端降水影响分析

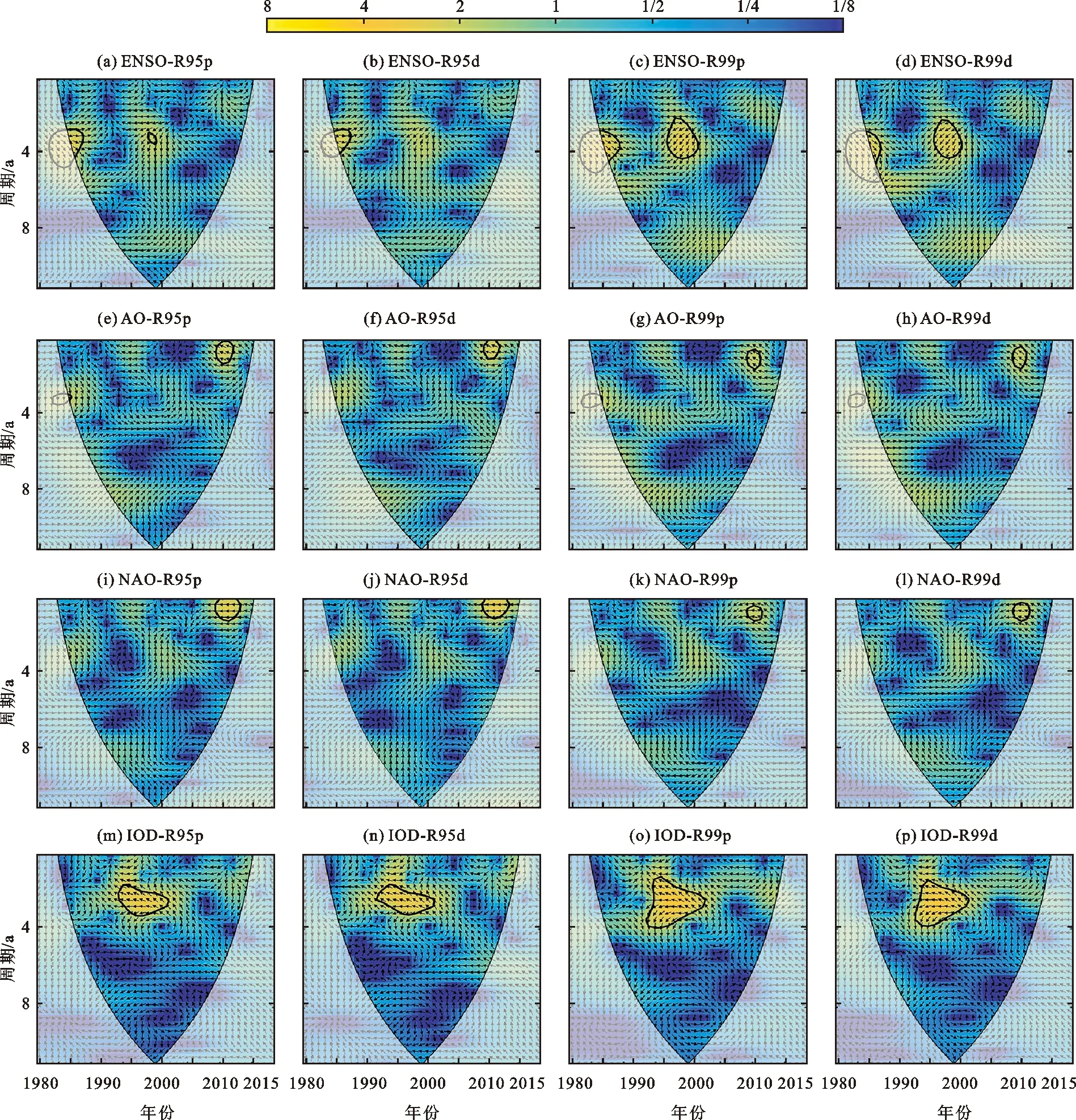
3.3.1 交叉小波分析 对极端降水指数与大气环流指数的连续小波变换后的系数进行双时间序列的交叉小波变换以及小波相干变换，以分析其显著时段、共振周期及位相关系等。其中，交叉位相以弧度表示，“±”之前的数值为平均位相角，“±”之后的数值为位相角计算中的卷积误差。大气环流指数与极端降水指数的交叉小波功率谱如图4所示。

由图4可知，ENSO与R95p在1985-1987年间具有3.28～4.13 a的显著共振周期，交叉位相为0.531 5±0.327 0 rad，ENSO提前于R95p约34.5 d(图4(a))；与R95d在1985-1987年间具有3.48～3.90 a的显著共振周期，交叉位相为0.386 3±0.615 9 rad(图4(b))；与R99p在1985-1987年间具有3.47～4.83 a的显著共振周期，交叉位相为0.659 6±0.255 8 rad，ENSO提前于R99p约37.79 d，此外，在1996-2000年间具有3.10～4.13 a的显著共振周期，交叉位相为2.279 6±0.294 0 rad，ENSO提前于R99p约130.61 d(图4(c))；与R99d在1996～2000 a间具有3.10～4.12 a的显著共振周期，交叉位相为2.279 6±0.279 3 rad，ENSO提前R99d约130.60 d(图4(d))。

AO与R95p在2009-2011年间具有2.19～2.46 a的显著共振周期，交叉位相为-2.951 6±0.603 2 rad，AO延后于R95p约169.11 d(图4(e))；与R95d在2010-2011年间具有2.19-2.46 a的显著共振周期，交叉位相为2.824 1±0.082 8 rad，AO延后R95d约161.81 d(图4(f))；与R99p在2009-2010年具有2.32～2.60 a的显著共振周期，交叉位相为2.735 9±0.680 7 rad，AO延后R99p约156.74 d(图4(g))；与R99d在2009-2010年间具有2.32～2.60 a的显著共振周期，交叉位相为2.473 4±0.041 2 rad，AO延后R99d约141.73 d(图4(h))。

NAO与R95p在2009-2012年间具有2.07～2.46 a的显著共振周期，交叉位相角为3.140 3±0.041 7 rad，NAO提前R95p约179.93 d(图4(i))；与R95d在2009-2013年间具有2.07～2.46 a的显著共振周期，交叉位相角为3.111 9±0.076 4 rad，NAO提前于R95d约178.30 d(图4(j))。与R99p在2009-2011年间具有2.32～2.46 a的显著共振周期，交叉位相角为2.907 6±0.157 9 rad，NAO延后R99p约166.59 d(图4(k))；与R99d在2009-2011年间具有2.19～2.46 a的显著共振周期，交叉位相角为2.853 6±0.110 2 rad，NAO延后R99d约163.50 d(图4(l))。

IOD与R95p在1993-2000年间具有2.76～3.74 a的显著共振周期，交叉位相角为2.773 0±0.334 7 rad(图4(m))，IOD延后R95p约158.88 d；与R95d在1991-1999年间具有2.76～3.74 a的显著共振周期，交叉位相为2.773 0±0.334 7 rad，IOD延后R95d约159.39 d(图4(n))；与R99p在1992-2000年间具有2.60～3.90 a的显著共振周期，交叉位相为3.054 9±0.727 9 rad，IOD延后R99p约175.03 d(图4(o))；IOD与R99d在1992-2000年具有2.60～3.90 a的显著共振周期，位相角为3.123 7±0.616 8 rad，IOD延后R99d约178.97 d(图4(p))。EASM与PDO对极端降水指数的影响不显著。

3.3.2 小波相干分析 大气环流指数与极端降水指数的交差小波凝谱如图5所示。由图5可知，EASM与R95p在1989-1996年具有5.84～8.76 a的显著共振周期，交叉位相为1.561 0±0.254 4 rad，EASM延后R95p约89.44 d(图5(a))。EASM与R95d在1980-1985年具有6.95～9.83 a的显著共振周期，交叉位相为1.823 0±0.172 0 rad，EASM延后R95d约104.45 d，在2008-2010年间具有5.12～6.56 a的共振周期，交叉位相为2.612 6±0.143 6 rad，EASM延后R95d约149.69 d(图5(b))。EASM与R99p在1989-1994年具有6.19～6.95 a的显著共振周期，交叉位相为1.612 4±0.074 9 rad，EASM延后R99p约92.38 d；在2011-2013年具有2.46～3.47 a的显著共振周期，交叉位相为1.817 0±0.150 0 rad，EASM提前R99p约104.10 d(图5(c))；与R99d在1985-1986年具有2.60～3.47 a的显著共振周期，交叉位相为2.885 7±0.200 3 rad，EASM延后R99d约165.34 d；在1989-1995年间具有5.85～7.36 a的显著共振周期，交叉位相角为1.875 2±0.119 6 rad，EASM延后R99d约107.44 d；此外，在2012-2014年间具有2.76～3.47 a的显著共振周期，交叉位相为2.056 9±0.124 8 rad，EASM提前R99d约117.85 d(图5(d))。

ENSO与R95p在2004-2013年间具有3.47～5.52 a的显著共振周期，交叉位相为1.026 5±0.338 3 rad，ENSO提前R95p约58.81 d(图5(e))。ENSO与R95d在1996-2012年具有4.13～5.84 a的显著共振周期，交叉位相角为1.020 0±0.447 3 rad， ENSO提前R95d约58.44 d(图5(f))；与R99p在2009-2013年具有2.92～4.64 a的显著共振周期，交叉位相角为1.699 4±0.740 2 rad，ENSO比R99p提前97.37 d(图5(g))。ENSO与R99d在2009-2013年间具有3.82～4.91 a的显著共振周期，交叉位相角为1.966 2±0.616 7 rad，ENSO提前R99d约112.65 d(图5(h))。

AO与R95p在1985-1987年具有2.76～3.10 a的显著共振周期，交叉位相角为1.394 6±0.103 6 rad，AO提前R95p约79.90 d；在1989-1994年具有5.84～8.76 a的显著共振周期，交叉位相角为0.272 6±0.397 5 rad，AO延后R95p约15.62 d；此外，在2008-2010年具有2.07～2.32 a显著共振周期，交叉位相角为2.667 9±0.057 2 rad，AO延后R95p约152.86 d(图5(i))。AO与R95d在1985-1987年间具有3.10～3.47 a的显著周期，交叉位相角为1.360 3±0.102 6 rad，AO提前R95d约77.94 d，在1991-1997年间具有7.36～9.28 a的显著共振周期，交叉位相角为0.581 7±0.141 2 rad，AO延后R95d约33.33 d(图5(j))。AO与R99p在1989-1992年间具有5.84～6.95 a的显著共振周期，交叉位相角为0.155 1±0.120 6，AO提前R99p约8.89 d，在1994-1995年间具有2.07～2.60 a的显著共振周期，交叉位相角为2.792 0±0.112 0 rad，AO延后R99p约159.97 d，在2009-2010年间具有2.19～2.60 a的显著共振周期，交叉位相角为2.583 2±0.048 3 rad，AO延后R99p约148.01 d(图5(k))。AO与R99d在1989-1993年具有5.84～6.95 a的显著共振周期，交叉位相角为0.113 1±0.125 8 rad，AO延后R99d约6.48 d，在2008-2012年具有2.07～2.76 a的显著共振周期，交叉位相角为2.490 3±0.116 6 rad，AO延后R99d约142.68 d(图5(l))。NAO以及PDO与极端降水指数之间的显著共振周期、显著时段、交叉位相以及时间间隔，如表2所示，而IOD对极端降水指数的影响不显著。

注：细弧线为小波影响锥曲线；黑粗线为95%置信区间；箭头表示相对位相差，“→”表示两者变化位相一致，“←”表示两者变化位相相反，“↑”表示大气环流指数延后于极端降水指数，“↓”表示大气环流指数提前于极端降水指数(下同)。

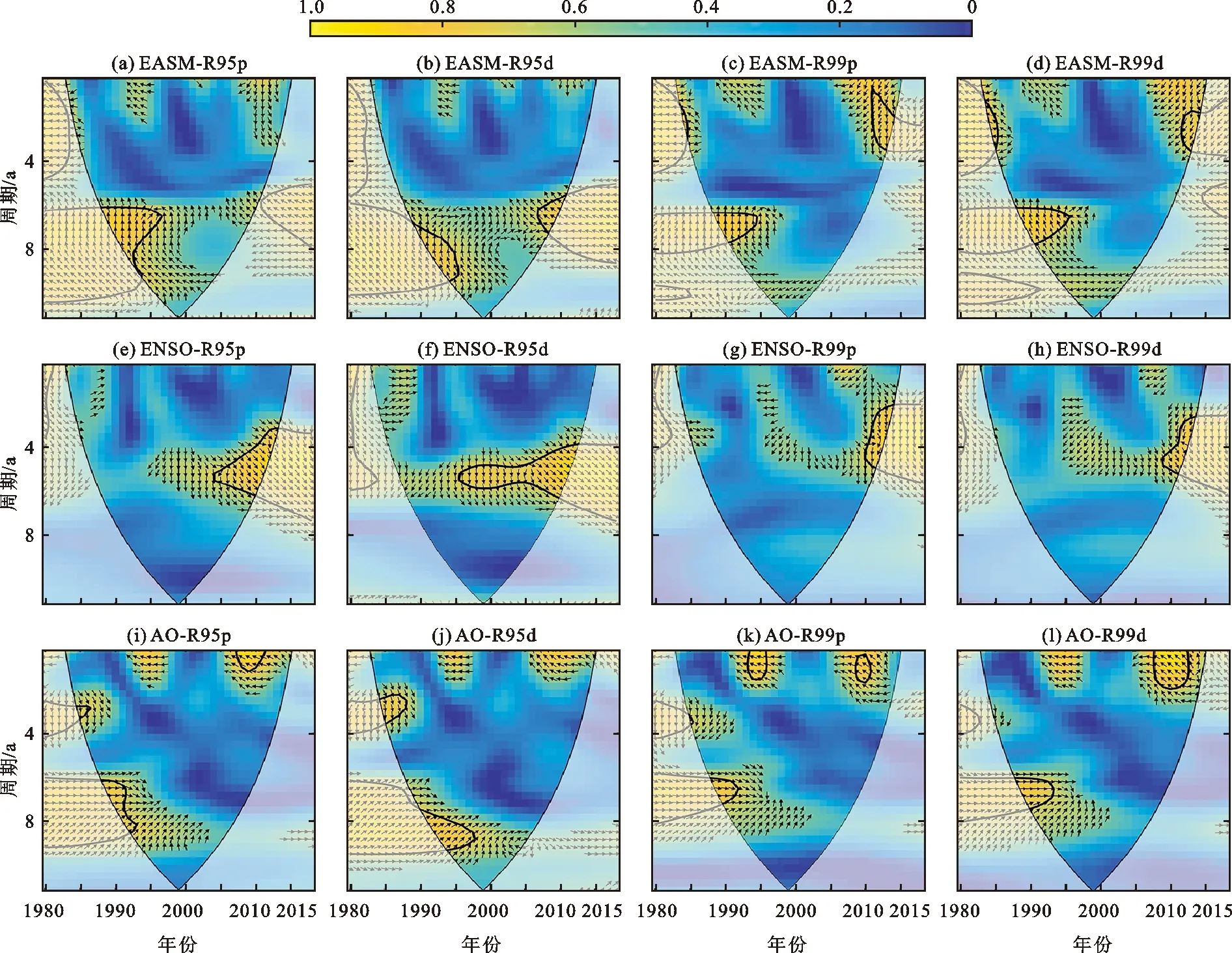
图5 大气环流指数与极端降水指数的交叉小波凝聚谱

4 讨 论

大气涛动是控制一个地区的大气环流机制，研究极端降水变化与大气涛动的相互关系有助于认识区域极端降水变化的特征和形成机制。本文的小波变换分析结果显示，长江中下游地区极端降水与大气涛动确实存在年际和年代际尺度显著共振周期，只是不同时域上存在明显差异。这至少说明大尺度的气候因子作为外部驱动力影响极端降水变化是长江中下游地区极端降水发生年际和年代际变化的重要原因之一。

作为具有稳定的西南或东南气流，EASM的变化主要受亚洲大陆与其周围海温之间热力差异的影响，它能将热带海洋上的充沛水汽持续不断地输送到东亚地区。本文研究进一步分析发现，EASM与长江中下游地区极端降水指数具有显著负相关关系，当发生一次强的EASM(正高值)时，长江中下游地区随后几年极端降水偏少，这与张璟等[27]的研究结果大致一致。余荣等[14]在研究中发现，厄尔尼诺次年西太平洋副热带高压西伸加强，则与其相关的东南季风所输送的水汽也有所加强，同时，中高纬度阻塞高压环流形势稳定维持。受这些因子的共同作用，最终导致长江中下游地区极端降水增多。张勇等[28]的研究中指出，当AO呈正位相环流特征时，不利于冷空气南充，从而导致沿江地区降水偏少。NAO与AO本质上是一致的，NAO是AO在北大西洋区域的一种表现形式。NAO既具有显著的年代际振荡周期，同时与长江中下游地区极端降水状况具有很好的对应关系。PDO是一种类似于ENSO的太平洋气候变动过程，指示着北太平洋海洋表面高温度的变化过程。其年代际变化对东亚大气环流异常具有重要作用，与EASM有很好的一致性，而且在年代际尺度上具有显著的正相关关系。于淼等[29]在研究中也指出，PDO与中国东部季风区夏季降水时空分布的关系是:PDO处于暖位相时，长江中下游地区降水异常偏多;PDO处于冷位相时,则与上述情况相反。IOD是一种海洋-大气耦合现象，它的定义为热带西印度洋与热带东南印度洋之间的海温异常。研究表明, 当印度洋偶极子指数为正位相时, 汛期华北及江淮流域干旱少雨, 而华南沿海地区为多雨带;反之, 汛期雨带分布基本为南北多雨而长江流域少雨[30]。这些结论与本文研究结果相一致。

但交叉小波图及小波相干图显示，在有些年份EASM、ENSO、AO、NAO、PDO以及IOD对该地区极端降水的影响并不强烈。这说明极端降水结构不仅受大气环流异常因子的影响，还可能受其他因素的影响。如地形的屏障作用、冬季青藏高原积雪等。极端气候事件有时并不是由于极端的外部强迫因子造成的，很可能是由于气候因子自身的内部波动引起的。在今后的研究中，需要考虑这些因素，以期得到更加充足的结论。

5 结 论

使用1980-2018年长江中下游地区气象站点资料，结合同期的大气环流指数，对长江中下游地区的极端降水指数周期性变化过程及对大气环流指数的响应进行详细分析，主要结论如下。

(1)所有的极端降水指标都存在多尺度周期性震荡，R95p以3.47 a为第一主周期；R95d以2.25 a为第一主周期，3.47 a为第二主周期；R99p和R99d均以3.79 a为第一主周期。各指标的周期性震荡趋向于高时频尺度，“增加-减少”变化更加频繁。

(2)大气环流指数在20世纪80年代中期至90年代中期均出现显著周期。EASM以2.92 a为第一主周期；ENSO以3.79 a为第一主周期，5.36 a为第二主周期；AO以4.13 a为第一主周期；NAO以2.25 a为第一主周期，以3.47 a为第二主周期；PDO以5.36 a为第一主周期；IOD以2.92 a为第一主周期。

(3)极端降水指数与大气环流指数在年际尺度上均存在一定的共振周期，但在不同时域中存在明显差异。EASM与PDO在高能量谱区对长江中下游地区极端降水的影响较弱。IOD在低能量谱区对极端降水指数影响较弱。