某垃圾填埋场氯化物运移的不确定性分析

李登波， 邓 芳， 唐玉川， 张建民

(1.中国电建集团中南勘测设计研究院有限公司， 湖南 长沙 410014； 2.中国长江三峡集团有限公司， 北京 100038；3.四川大学 水力学与山区河流开发保护国家重点实验室， 四川 成都 610065)

1 研究背景

地下水溶质运移受到多方面的影响，其中水文地质参数的不确定性是影响模型准确性的主要原因[1]。边界条件或地质地貌改变都可能导致该研究区的水文地质参数发生变化，另外因含水介质形成条件的复杂性，导致大多数水文地质参数，比如渗透系数、孔隙度等具有空间变异性[2-4]。对于非均质介质中的溶质运移问题，水文地质参数的不确定性对于溶质运移有着重要的影响。Freeze的研究表明了渗透系数服从对数正态分布，后来这一结论也被一些学者的研究证明[5]。杨助泽[6]、李少龙等[7]和宋浩等[8]通过建立随机数学模型得到了水文地质参数的空间变异性对水头分布的影响。蒋立群等[9]和施小清等[10]通过随机模拟法研究了水文地质参数的空间变异性对氯化物运移结果的影响。王建娥等[11]基于Choleshy分解进行了堆石材料的参数随机场模拟，通过随机有限元模型进行计算，得到了随机有限元模型计算结果比常规有限元计算结果更接近实测值的结论。综上所述，随机模拟法可以较好地考虑到水文地质参数不确定性的影响，从而对地下水溶质运移有更为准确的描述。

本文分别考虑了水文地质参数数值不确定性和空间分布随机性两种因素对于氯化物运移的影响，定量比较了氯化物浓度和污染范围的不确定性。在水文地质参数空间分布随机性方面，基于3种空间插值技术对渗透系数的空间分布进行随机模拟计算。通过不确定性分析可以掌握该地区氯化物浓度的变化范围，在划分不同浓度置信区间的基础上进行风险分析，以期为地下水污染防治提供数据参考。

2 数据来源与研究方法

2.1 研究区概况

某垃圾填埋场位于非承压含水层，含水层在该区域西南部最厚，在该区域的北端变薄至9.5 m，该含水层的厚度为15～30 m不等，为冰川河流砂含水层，含水层埋深较浅，底部由大面积的黏土质和砂质淤泥层构成相对隔水屏障。含水层主要由细粒、中粒和粗粒砂组成复杂地层，由于透镜体的存在使得非承压含水层局部是非均匀的，研究区内的各水文地质参数存在一定的变化范围，表1为研究区水文地质参数变化范围表，参数的变化在其均值的20%范围内。

表1 研究区水文地质参数变化范围表

根据已有资料建立该地区的地下水数值模型，如图1所示。其中网格剖分采用结构化网格，网格总体数量为119 240个，最大网格尺寸为280 m。含水层补给来源为降水入渗，排泄为侧向流出。上、下游为给定水头边界条件，每个月的水位随着季节变化但是变化不大，上游边界平均水头为222.2 m，下游边界平均水头为218.5 m，左、右边界条件为零流量边界条件。研究区垃圾渗滤液入渗区位置如图1所示，假设在某时刻垃圾场渗滤液开始渗漏并影响含水层，将垃圾渗滤液浓度概化为一个连续变化函数，浓度变化为先增大后逐渐减小最终保持稳定，其在第30 a时浓度达到最大值。

图1 研究区模型建立及其边界条件

2.2 数据来源

本文的研究区位于加拿大多伦多以北约100 km处的某军事基地，该填埋场启用于1940年，一直使用至1976年。在1974-1980年期间，该地区逐渐建立起大量立式压力计用于监测该地区地下水位值，文献[12]给出了该地区1983年的实测水位场分布图。另外在含水层范围内有80台多级监测仪，从820个采样点中获取了氯化物的空间浓度值，并绘制了垃圾填埋场运行第43 a(1983年)时的氯化物浓度实测分布图。根据Macfarlane等[13]和Cherry等[14]的研究成果，得到了该地区的渗透系数和孔隙度等水文参数的实测值，Sudicky[15]通过研究得到了该地区的弥散系数的实测值，本文基于这些文献的实测资料值，对该地区氯化物的运移情况进行了不确定性分析。

2.3 研究方法

2.3.1 计算模型

(1)地下水流运动模型。考虑到该研究区为非均质各向异性三维含水层，其控制方程可以用如下公式表示：

(1)

式中：K为渗透系数，m/d；μs为贮水率，m-1；H(x,y,z)为边界Г1上的水头，m；φ(x,y,z)为边界Г1上的已知函数；H0(x,y,z)为t=0时边界D上的初始水头，m；Ω为研究区域； Г1、D为边界条件。

(2)地下水对流-弥散方程。 该垃圾填埋场氯化物渗滤液的运移，其控制方程可以用如下公式表示：

(2)

式中：Dxx为纵向弥散系数，m2/s；Dyy、Dzz为横向弥散系数，m2/s；ux、uy、uz为实际平均流速在坐标轴的3个分量，m/s；c(x,y,z,t)为边界Г1上的浓度，kg/m3；φ(x,y,z,t)为边界Г1上的已知函数；c0(x,y,z)为t=0时边界D上的初始浓度，kg/m3。

随机模型即在上述常规数值模型的基础上考虑了参数的数值不确定性和空间分布随机性，将得到的不同参数组合或者满足一定空间分布状态的输入参数代入到模型中进行多次蒙特卡洛计算，最后进行计算结果的统计规律分析。

2.3.2 插值方法

(1)反距离权重插值。反距离权重插值(inverse distance weighted， IDW)使用一组采样点的线性权重组合来确定像元值的方法。现有n个离散点Z(x1,y1,z1)，Z(x2,y2,z2)，…，Z(xn,yn,zn)，需要对插值点(x,y,z)进行插值预测[16]：

(3)

式中：F(x,y,z)为插值点(x,y,z)处的插值函数；wi为各个散点的权值函数；Qi为插值点的梯度超平面。

(2)克里金插值。克里金法(Kriging)最早是由法国著名统计学家Matheron和南非矿山地质工程师Krige提出的，它是一种数学内插及外推方法[17]。克里金模型中自变量与响应值之间的关系可以用下式表示[18-19]：

(4)

式中：Z*(x)为x处克里金法响应值；λi为满足无偏和估计方差最小两个条件的待定权重系数；Z(xi)为第i个位置处的实际观测值。

(3)自然邻域插值。自然邻域插值法(natural neighbor， NN)可找到距离查询点最近的输入样本子集，并基于区域大小按照比例对这些样本根据权重进行插值。当求某一位置点的预测值时，按下式进行计算[18]：

(5)

式中：f(x)为x处的预测值；Ni(x)为x点关于其自然邻域节点的权重；fi为已知点函数值。

2.3.3 溶质运移结果的不确定性评价 为了定量描述氯化物运移结果的不确定程度，引入平均偏差值AEAE和平均方差值AESD两个参数共同来描述计算结果的不确定性程度[20-21]。AEAE用于描述模拟值较实测值的偏差程度；AESD用于说明计算结果距离模拟值均值的波动程度，其表达式如下：

(6)

(7)

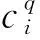
3 结果与分析

3.1 水文地质参数数值不确定性对模拟结果的影响及分析

通过参数灵敏度分析计算可知影响氯化物浓度最大的4个参数分别为水平渗透系数Kx、孔隙度n、垃圾填埋场处的入渗强度R和纵向离散度αL，因而取该4个水文地质参数进行数值不确定性分析。假设该4个水文地质参数在研究区内相互独立且均匀分布，每次随机模拟时在每个参数取值范围内随机抽取1个值并将其与其他3个参数进行组合，剩余水文地质参数计算时采用平均值，由此得到了1组输入参数样本值；将其代入随机数值模型中进行计算得到1次蒙特卡洛随机模拟结果。进行100次蒙特卡洛随机模拟，统计100次随机模拟结果值，得到了垃圾填埋场运行第43 a(1983年)4个监测点W2、W3、W4和W6处(位置分布见图1)的氯化物浓度统计参数值，表2为该4个监测点浓度分布参数统计表。其中，最优值是将浓度范围等分为20个区间，取相对频率最大的区间浓度中点值。

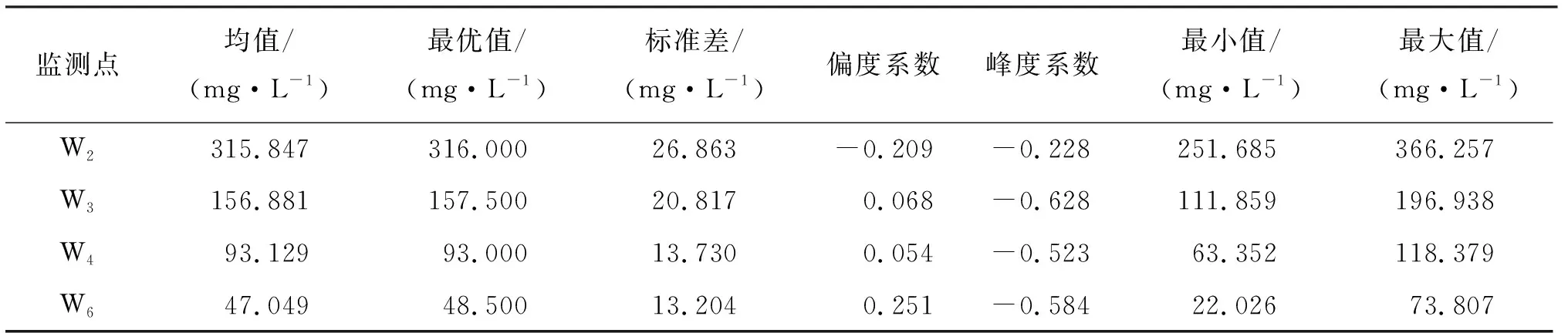
表2 4个监测点浓度分布参数统计表(1983年)

由表2可知，统计第43 a监测点W2的氯化物浓度分布区间为251.685～366.257 mg/L，氯化物浓度集中分布在316.000 mg/L，其平均浓度为315.847 mg/L；氯化物浓度分布偏度系数为-0.209，稍有负偏；峰度系数为-0.228，即氯化物浓度分布范围较正态分布模型稍大，直方图呈“矮胖”分布；对于监测点W3，氯化物浓度范围为111.859～196.938 mg/L，氯化物浓度集中分布在157.500 mg/L，其平均浓度为156.881 mg/L；其浓度分布偏度系数为0.068，基本呈对称分布；峰度系数为-0.628，即氯化物浓度分布范围较正态分布模型偏大，有“肥尾”现象；监测点W4氯化物浓度范围为63.352～118.379 mg/L，氯化物浓度集中分布在93.000 mg/L，其平均浓度为93.129 mg/L；氯化物浓度分布偏度系数为0.054，稍有“正偏”；峰度系数为-0.523，即氯化物浓度分布范围较正态分布模型大，直方图呈“矮胖”分布；监测点W6氯化物浓度范围为22.026～73.807 mg/L，其中氯化物浓度主要分布在48.500 mg/L，其平均浓度为47.049 mg/L；氯化物浓度分布偏度系数为0.251，呈“正偏”分布；峰度系数为-0.584，即氯化物浓度分布范围较正态分布模型稍大，直方图呈“矮胖”分布。

图2为实测水位平均值与多次蒙特卡洛随机模拟计算的平均值对比图。由图2可以看出，考虑参数数值不确定性的随机模型水头分布与实测水头平均值符合较好，具有良好的适用性。

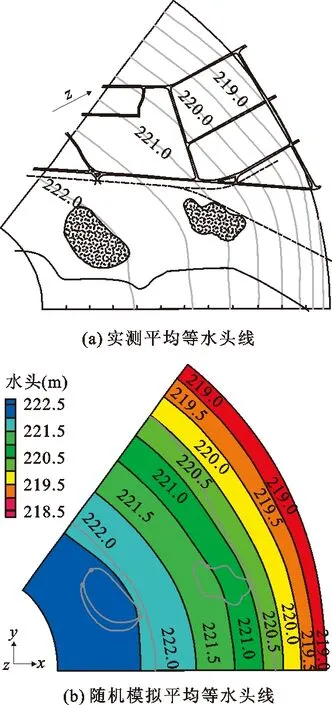
图2 研究区实测水位与随机模拟水位分布(单位：m)

绘制了数值不确定性情况下垃圾填埋场运行第43 a多次随机模拟平均氯化物浓度分布图，图3为图1中垃圾填埋场A-A断面的剖切图。由图3可见，考虑数值不确定性计算得到的50 mg/L氯化物等浓度曲线在水平及垂直方向上的范围与实测值范围相同，400 mg/L等浓度曲线的范围要大于实测值的浓度范围。

图3 研究区A-A断面数值模拟的平均氯化物浓度与实测值对比

考虑到氯化物监测点浓度的不确定性，本研究对监测点浓度的不同置信水平浓度区间进行了划分，表3为第43 a监测点的百分位点浓度表。其中90%的置信水平浓度区间是监测点5%～95%之间的浓度，其他置信水平浓度区间以此类推。由表3可见监测点W290%的置信水平浓度区间为[265.211 mg/L，360.184 mg/L]，监测点W390%的置信水平浓度区间为[123.320 mg/L，195.231 mg/L]，监测点W490%的置信水平浓度区间为[72.580 mg/L，114.238 mg/L]，监测点W690%的置信水平浓度区间为[24.633 mg/L，68.833 mg/L]，其他年份的置信水平浓度区间同理可得。随着监测点距离垃圾入渗区距离的增加，同等条件下氯化物浓度变化范围逐渐减小，氯化物浓度的不确定性逐渐减小。

表3 研究区4个监测点第43 a的氯化物百分位点浓度 mg/L

为了研究60 a计算时间段内水文地质参数数值不确定性对垃圾填埋场氯化物浓度不确定性影响的变化情况，计算了整个研究区垃圾填埋场运行60 a内即1940-2000年各时间节点的AEAE和AESD两个参数值，其结果如表4所示。

表4 研究区各时间节点的AEAE和AESD计算结果 mg/L

表4中的数值结果显示，研究区内氯化物浓度变化幅度会随着时间的改变而发生变化，氯化物浓度变化幅度越大，表明其不确定性也越大。从第10 a到第43 a，研究区内AEAE和AESD不断增加，表明其不确定性也逐渐增加，到第43 a达到最大值，AEAE和AESD分别为15.187和18.600；而后到第60 a逐渐减小，其不确定性也逐渐减小。就60 a整个计算时间段内变化趋势而言，数值不确定性对垃圾填埋场氯化物浓度的影响在第43 a最大。分析出现在第43 a的原因是污染源浓度在第30 a达到最大值，而由于地下水氯化物运移的滞后效应，所以氯化物浓度不确定性的最大值没有与污染源浓度最大值出现在同一年。

由于水平渗透系数Kx、孔隙度n、垃圾填埋场处的入渗强度R、纵向离散度αL对氯化物渗滤液输入量有影响，当该4个参数存在不确定性时，导致氯化物渗滤液入渗量存在不确定性，随着氯化物浓度逐渐增大，其入渗量的变化范围也逐渐增加，由于污染物的滞后效应，研究区氯化物浓度的AEAE和AESD两个参数值逐渐增加并在第43 a达到极值，随着氯化物入渗量变化范围的减小，两个参数值逐渐减小。

3.2 水文地质参数空间分布随机性对模拟结果的影响及分析

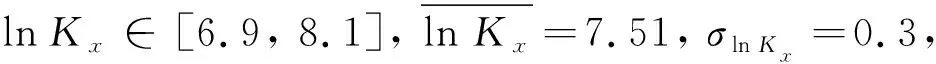
比较计算结果可知，3种空间插值手段均值差异不大，因此本文以IDW法计算得到的平均浓度为例。图4为考虑水平渗透系数空间分布随机性条件下，随机模拟平均值与实测氯化物浓度的对比。由图4可见，考虑渗透系数空间分布随机性模拟的浓度平均值较参数不确定性计算的平均值在极值浓度的分布范围上有所减小，极值浓度的位置也与实测值位置更为吻合。

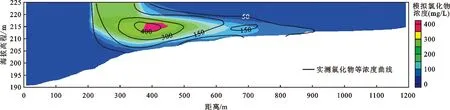
图4 研究区A-A断面数值模拟的平均氯化物浓度与实测值对比(考虑水平渗透系数空间分布随机性)

仍选取W2、W3、W4和W6共4个监测点，比较了水平渗透系数在空间分布随机性的情况下对氯化物浓度的影响，结果见图5。由图5首先可以看到，相比于确定性模型，由于受到水平渗透系数的空间分布随机性的影响，3种空间插值方法下模拟的各监测点氯化物浓度不再是一个确定的值，而是一个变化的浓度范围，该范围包含所有可能解。

图5 3种空间插值方法下4个监测点氯化物浓度的变化范围和标准差(第43 a)

不同监测点的浓度变化范围和标准差随着距垃圾渗滤液入渗区距离的增大而减小，表明氯化物浓度的不确定性逐渐减小，虽然垃圾渗滤液入渗浓度为确定值，但受到水平渗透系数的空间分布随机性的影响，研究区监测点浓度为一个变化范围，表明水文地质参数的空间随机分布对于浓度影响较大。其次对比空间随机性的3种空间插值方法，3种方法对各监测点氯化物浓度均值的影响均较小，但是对于氯化物浓度的变化范围和标准差，Kriging方法计算的结果最小，其次为NN方法，而IDW方法计算的结果最大。这说明3种随机模拟方法中，计算结果的不确定性程度最小的是Kriging法，其次是NN法，而IDW方法不确定性程度最大，表明在数值模拟中采用不同的空间插值方法实现参数空间分布随机性最终会使得计算结果的不确定性程度有所差别。

根据3种随机模拟方法下氯化物浓度的不确定性分析，进行了监测点浓度的置信区间划分，图6为第43 a研究区4个监测点浓度置信区间划分。其中90%的置信区间是监测点百分位5%～95%之间的浓度，其他置信区间依此类推。就同一种空间插值方法，80%置信浓度区间的长度小于90%置信浓度区间的长度，随着监测点远离垃圾渗滤液入渗点，它们之间的差距进一步减小，对比3种随机模拟方法的90%置信浓度区间可知，Kriging法计算的置信浓度区间范围最小，NN法次之，而IDW法置信浓度区间范围最大。

图6 研究区4个监测点浓度的置信区间划分(第43 a)

为了研究60 a计算时间段内水文地质参数空间分布随机性对垃圾填埋场氯化物浓度不确定性影响的变化情况，本研究针对AEAE和AESD两个参数进行了分析计算。表5中列出了采用3种不同空间插值方法时，研究区AEAE和AESD系数的计算结果。由表5中的计算结果首先得到的结论是：水平渗透系数的空间随机分布场对氯化物浓度计算结果有影响，且随着时间的推移，其影响程度也随之改变，呈现出先增加后减小的趋势。

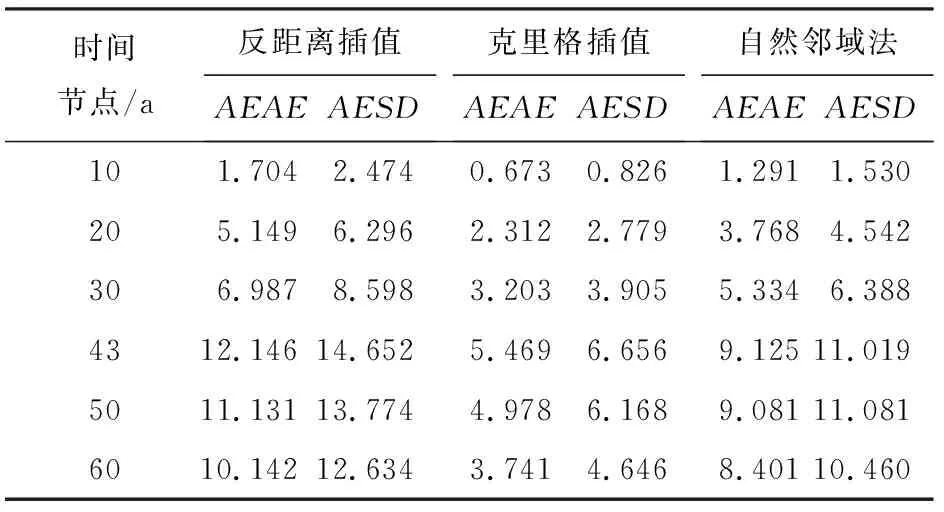
表5 研究区AEAE和AESD参数的3种不同空间插值法计算结果 mg/L

具体而言，3种插值方法在第10 a至第43 aAEAE和AESD值逐渐增加，第43 a达到最大，表明该时间节点氯化物浓度变化幅度最大，其不确定性达到最大；在43 a至60 a逐渐稳步减小，表明该时段氯化物浓度变化幅度逐渐减小，其不确定性逐渐减小。对比3种空间插值方法，对于同一年份，Kriging法计算的AEAE和AESD两个参数均较小，如在第43 a，Kriging法的AEAE和AESD分别为5.469和6.656 mg/L，其值为IDW法的45.03%和45.43%，NN法的59.93%和60.40%。说明Kriging方法得到的水平系数空间分布场，其计算的氯化物浓度不确定性最小，NN法次之，IDW法的不确定性最大。在AEAE和AESD最大值出现的时间上，3种空间插值方法的随机模拟最大值均出现在第43 a。

将水文地质参数空间分布随机性的3种空间插值方法和水文地质参数数值不确定性计算的AEAE和AESD进行比较，绘制了该4种方法的AEAE和AESD计算结果，如图7所示。首先，氯化物浓度不确定性最大的排序为参数数值不确定性>空间分布随机性。其次，对比60 a内3种插值方法AEAE和AESD变化趋势的空间分布随机性，其排序为：反距离插值(IDW)法随机模拟>自然邻域(NN)法随机模拟>克里格插值(Kriging)法随机模拟。在AEAE和AESD最大值出现的时间上，在计算的60 a范围内参数数值不确定性和空间分布随机性最大值均出现在第43 a，而污染源浓度在第30 a达到最大值，由于地下水氯化物运移的滞后效应，研究区内垃圾渗滤液入渗量也滞后出现。无论是参数数值不确定性还是空间分布随机性主要是由垃圾渗滤液入渗量决定最终计算结果，其不确定性程度大小与垃圾渗滤液入渗量成正比。

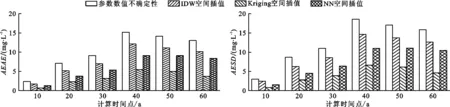
图7 4种方法计算的AEAE和AESD结果对比

4 结 论

(1)不确定性模型随机解的均值体现了地下水系统的结构性，它的极值和标准差又体现了地下水系统的随机性。相比于确定性模型，不确定性模型更能体现出其在实际应用中的优势。

(2)地下水溶质运移受到参数数值不确定性和空间分布随机性影响，在输入参数±20%变化范围内，本案例中参数数值不确定性影响较空间分布随机性影响程度大。

(3)在60 a的计算时间内3种空间插值方法中，Kriging法得到的水平系数空间分布场，其计算的氯化物浓度不确定性最小，以43 a为例，AEAE和AESD参数值仅为同时间IDW法的45.03%和45.43%，NN法的59.93%和60.40%。

(4)在60 a的计算时间内，参数数值不确定性和空间分布随机性最大值都滞后出现(第43 a)，说明无论是参数数值不确定性还是空间分布随机性均是通过影响垃圾渗滤液的入渗量来影响最终计算结果的。