一-种具有无功补偿能力、无电解电容的单级光伏逆变器

孙 玥，桂 冠

（1.南京信息职业技术学院 智能交通学院，江苏 南京210023；2.南京邮电大学 通信与信息工程学院，江苏南 京210023）

0 引言

太阳电池板的输出电压受到天气、光照等环境因素的影响，无法将光伏板产生的最大功率直接传输到电网，须要在光伏板旁使用逆变器克服这些限制。单相光伏逆变器的输入电压存在二倍工频的波动[1]。对此，无源解耦电路因控制简单、结构经济而被广泛采用，但输出端电容值需求较大，往往采用电解电容方能满足要求[2]。相较于无源解耦，有源解耦可有效解决电解电容受温度等因素影响寿命低的问题，其实质是创造一新的能量路径来消纳二倍工频谐波。因此，它需要一个附加有源和无源元件的消纳端口，从而增加了成本 [3]。

目前，电压和电流波形重塑技术因仅需要小型无源元件（例如小型薄膜电容）来处理脉动功率，无需电解电容或其他功率电路而受到了广泛关注[4]。文献[5]提出了一种基于改进控制算法（Control Algorithm Modification，CAM）的 输 入 电流重塑方法，该方法利用两个单独的控制器分别控制前级DC/DC变换器和后级DC/AC变换器。文献[6]提出了一种新的基于改进运行模态（Operation Mode Modification，OMM）的 波 形 整 形方案，该方案仅用单个控制器，在高频状态下协调输入和输出开关，使缓冲电容吸收/注入脉动功率。

与CAM方法相比，OMM具有以下优点：①仅需一个控制器；②控制算法易实现；③不需要直流电压传感器，成本低；④在单输入模式的逆变器中只有单级转换并且只有两个开关工作在高频状态，效率高。鉴于此，本文提出一种新型的单级光伏逆变器拓扑，扩展了这种基于OMM的波形整形方法的应用。与文献[1]中的单输入模式逆变器相比，该逆变器减少一个二极管；此外，由于输入和输出共地，有效消除了共模电压对网侧电能的污染。

为满足发电系统或发电单元的功率因数在±0.9内可调[7]，[8]，本文提出了一种非单位功率因数运行的调制技术，可在并网模式下灵活控制有功功率和无功功率。在不改变逆变器结构的情况下，只须简单地修改运行模态和电流参考相移，即可实现无功补偿。

1 逆变器运行模态

本文所提逆变器拓扑（图1）采用TSS控制策略，该TSS控制器通过调节缓冲电容电压处理脉动功率，不影响输入直流或输出交流电流/电压。其中电容值表达式为

图1 所提单相逆变器拓扑Fig.1 Proposed single phase inverter topology

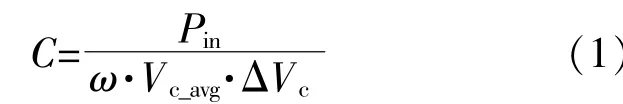
式 中：Pin，Vc_avg和 ΔVc分 别 为 输 入 功 率、电 容 上 的直流电压和二倍频纹波电压；ω为输出侧的基波角 频 率，ω=2πf，f为 电 网 频 率。

由于所提逆变器解耦电容两端可承受较大ΔVc，因此可以选择体积小、寿命长的薄膜电容作为缓冲电容。

1.1 当功率因数（Power Factor，PF）等于1时逆变器的运行模态

为处理输入功率Pin和输出功率Po（t）之间的功 率 脉 动，缓 冲 电 容 的 瞬 时 功 率Pc（t）和 电 压Vc（t）可 以 通 过 式（2），（3）确 定。

式 中：Vm，Im分 别 为 输 出 电 压Vg（t）和 电 流Ig（t）的幅值；Vc0为输出电流为零时的缓冲电容电压。

当PF=1时，输出电压和电流同相。

根 据 式（2），（3），图2给 出 了Vg（t），Ig（t），Pin，Po（t），Pc（t），Vc（t）的 波 形。当Pin＞Po（t）时，Vc（t）上升 储 存 能 量；当Pin＜Po（t）时，Vc（t）下 降 释 放 能 量。模 式1中，Ig（t）＞0，Vg（t）＞0；模 式2中，Ig（t）＜0，Vg（t）＜0。

图2 当PF=1时处理脉动功率时的关键波形Fig.2 The key waveform of pulse power processing when PF=1

为 调 节Vc（t），本 文 提 出TSS运 行 策 略，将 逆变器在每个开关周期Ts分为3个开关状态。图3给出了模式1和模式2下的3种模态。图4为每个开关状态期间Vc（t）变化示意图。如图3和图4所 示：在 状 态1[持 续 时 间t1（n）]（n为 第n个 采 样周期）中，电流流入缓冲电容，电压增加；在状态2[持 续 时 间t2（n）]中，缓 冲 电 容 输 出 电 流 放 电，电 压降 低；在 状 态3[持 续 时 间t3（n）=Ts-t1（n）-t2（n）]中，缓冲电容与电路断开，电压保持恒定。通过调节每个状态的持续时间来控制每个快速开关状态期间的Vc（t），使 得 在 每 个Ts期 间，缓 冲 电 容 可 以 吸 收该周期内的脉动功率。

图3 在一个开关周期内的3种快速开关状态Fig.3 Three fast switching states in one switching

图4 当PF=1时缓冲电容电压与所提TSS控制策略示意图Fig.4 The buffer capacitor voltage and the proposed TSS control strategy diagram when PF=1

如图3所示：在模式1中，S2始终打开，S1和S4始终关断，只有S0和S3在高频开关下切换以调节Vc（t）；在 模 式2中，S4导 通，S2和S3关 断，只 有S0和S1在高频开关下切换以调节Vc（t）。可以看出，两个开关管同时工作在高频，可减少开关的损耗。

如 图4所 示：当Pin＞Po（t）时，Vc（t）增 加[V3（n）＞Vx（n）]；当Pin＜Po（t）时，Vc（t）降 低[V3（n）＜Vx（n）]。两个相邻状态之间的电压关系，以及电容电流和电压变化的关系为

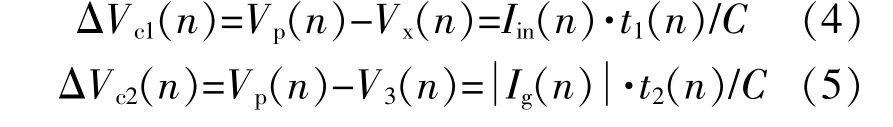
式 中：ΔVc1（n），ΔVc2（n）分 别 为 充 电 状 态1和 放 电状 态2时Vc（t）的 变 化 绝 对 值；Iin（n）为 光 伏 模 块直流输入电流；Ig（n）为开关周期n时的瞬时输出电流；Vx（n）为状态1开始时的缓冲电容电压；Vp（n）为 状 态1结 束 时 的 缓 冲 电 容 电 压；V3（n）为状态3时的缓冲电容电压。

根据电感伏秒平衡原理，可得输入侧直流电压Vin（n）为

经 式（10）～（12）计 算 出 持 续 时 间，从 而 产 生PWM信号，控制每个状态下的Vc（t）变化，以跟随由 式（8）和 式（9）确 定 的 指 令 值。

1.2 当PF≠1时逆变器的运行模态

当PF≠1时，缓 冲 电 容 的Pc（t）和Vc（t）可 由下式确定：

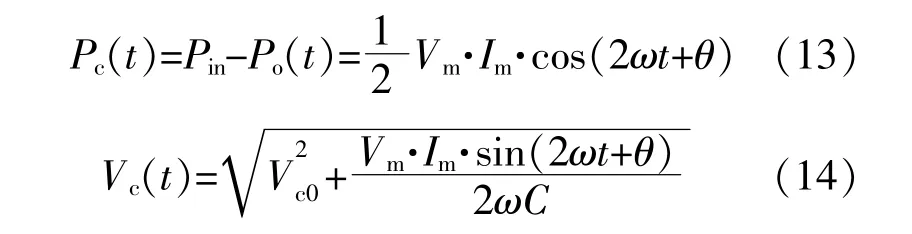
式 中：假 设Vc（t）初 始 相 位 角 为 零；θ为Ig（t）的 初始相位角。

图5给 出 了Vg（t），Ig（t），Pin，Po（t），Pc（t），Vc（t）的 波 形。当Pin＞Po（t）时，Vc（t）上 升 以 储 存 能 量；相反，当Pin＜Po（t）时，Vc（t）下 降 以 释 放 能 量。当PF≠1时，存在另外两种模式，即模式3和模式4。在模式3中，Ig（t）＞0，Vg（t）＜0；在 模 式4中，Ig（t）＜0，Vg（t）＞0。在 模 式1和 模 式2中，与 上 述 模 态 相 似，在此不做赘述。

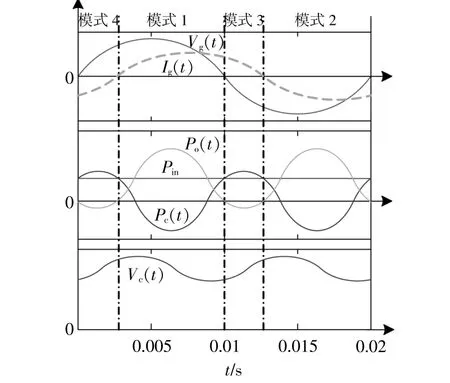
图5 当PF≠1处理脉动功率时的关键波形Fig.5 The key waveform of pulse power processing when PF≠1

模式3和模式4在每个恒定的Ts中也有3种快速开关状态。在模式3中，状态1和状态3的模态与模式1中的模态相同；在模式4中，状态1和状态3的模态与模式2中的模态相同 （图3）。图6给出了模式3和模式4中状态2的模态。图7为Vc（t）变 化 示 意 图。

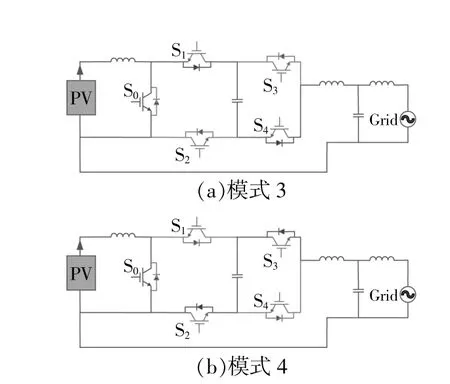
图6 状态2Fig.6 State 2

图7 当PF≠1时，缓冲电容电压与所提TSS控制策略示意图Fig.7 The buffer capacitor voltage and the proposed TSS control strategy diagram when PF≠1

如图6和图7所示：在模式3和模式4的状态1[t1（n）]期 间，电 流 流 入 缓 冲 电 容 充 电，电 压 上升；状 态2[t2（n）]期 间，缓 冲 电 容 进 一 步 充 电，电 压不断增加；状态3[t3（n）]期间，缓冲电容与电路断开，电压保持恒定。

对于模式3和模式4，状态2的持续时间计算式为

模式1和模式2在PF=1和PF≠1时的3种状态持续时间计算式是相同的。通过计算出3种状态的持续时间来产生PWM信号，控制Vc（t）在一个Ts内平均电压等于由式（14）确定的参考值。

2 控制策略

图8 所提逆变器控制策略Fig.8 The proposed inverter control strategy

3 比较分析

相较于文献[4]，[6]，本文采用三态开关控制策略，无须处理母线电压（即缓冲电容两端电压），减少了传感器数量和逻辑门数量，降低了控制复杂度，电路稳定性高。相较于文献[9]，本文通过多单元整合的方式大大降低了器件冗余度，有效减少了开关管和二极管的使用数量。因此，所提逆变器拥有较高的功率密度。

比较结果如表1所示。

表1 比较结果Table 1 Comparative results

4 实验验证

为了验证理论分析的正确性及所提逆变器的可行性，本文搭建了额定功率为80 W的实验样机。实验电路参数如表2所示。

表2 实验电路参数Table 2 Experimental circuit parameters

4.1 PF=1时的实验结果

图9给 出 了 最 大 功 率 点（MPPT）的Iin，Vin和Ig（t）的波形。如图所示：输入电流和电压逐渐达到MPPT的电流和电压；Ig（t）幅值在最大功率跟踪过程中逐渐增大，在MPPT附近运行时几乎保持不变，与理论分析一致。

图9 MPPT关键波形Fig.9 Key waveforms during MPPT

图10给 出 了 稳 态 运 行 时Iin，Vin，Ig（t）和Vc（t）的波形。结果表明：Vc（t）含有较大的二倍频纹波（100 Hz），峰峰值约为100 V；输入电流是恒定的直 流（2.1 A），输 入 电 压 也 为 恒 定 直 流（36 V）；电网电流为正弦交流（有效值为0.7 A），总谐波失真为2.1%。此时，样机效率高达91.5%。这些结果证实：①输入和输出之间的脉动功率由一个很小的缓冲电容来处理；②较大的Vc（t）纹波不影响输入直流和输出交流电流/电压；③减少对母线电容的依赖，最终仅需10μF薄膜电容即可。

图10 稳态运行时关键波形Fig.10 Key waveforms at steady-state

图11为Vc（t）在正半周期内的变化和开关模态。如 图 所 示，当Pin＞Po（t）时，Vc（t）增 加 以 存 储 能量。符合理论分析，反之亦然。

图11 缓冲电容电压和开关驱动信号Fig.11 Buffer capacitor voltage and switch drive signal

4.2 PF≠1时的仿真结果

设定逆变器在PF=0.7时运行，电网电流比电网电压滞后约45°。除了MPPT时电网电流有效值为1.2 A外，其余参数同表1。

图12给 出 了 稳 态 运 行 时Iin（t），Vin（t），Ig（t）和Vg（t）的波形。如图所示：输入电流和电压几乎是恒定的；电网电流为正弦交流，总谐波失真为2.3%，电网电流比电网电压滞后45 °。这证明了逆变器可以在非单位功率因数下运行，实现逆变器的无功补偿能力，在电压暂降和存在非线性负载的情况下加强配电网鲁棒性并改善供电质量。

图12 当PF=0.7时，稳态运行关键波形.Fig.12 Key waveforms at steady-state when PF=0.7

5 结论

本文提出了一种新型单相逆变器拓扑结构和TSS控制策略。使用TSS控制器，该逆变器缓冲电容可以容许存在较大的二倍频纹波，只需10μF薄膜电容即可运行，而不需要额外的解耦电路。同时，可以向电网注入无功功率。该逆变器具有寿命长、成本低、功率密度高和无功补偿等优点。实验结果验证了所提逆变器在单位功率因数和非单位功率因数下的有效性和设计的正确性。