基于Ziegler-Nichols优化算法的火电机组负荷频率PID控制研究

于国强，刘克天，胡尊民，汤可怡，史毅越

（1.江苏方天电力技术有限公司，江苏 南京 211102；2.南京工程学院电力工程学院，江苏 南京 211167）

近年来随着风电、光伏为代表的分布式新能源不断并入电网，电网系统负荷峰谷差逐渐加大，而电网的消纳能力有限，造成大量弃风弃光现象[1-2]。火电机组是电网调峰的主要电源，机组深度调峰运行时的二次调频动态特性引起了很多电网单位的高度关注，已有文献对调峰机组调频性能展开研究。

文献[3]针对常规机组和分布式新能源机组的负荷频率控制策略展开了比较研究。文献[4]将火电机组简化为典型的非线性动态模型，通过机理分析模型中主要参数的变化规律，进一步将控制方法应用于实际机组深度调峰中。Toulabi M R 等使用哈里通诺夫定理来设计电力系统的负荷频率控制，设计后系统鲁棒性良好[5]。文献[6]重新定义了外界扰动后的电力系统动态频率，目前得到了广泛的应用。火电机组进行深度调峰运行时，其一次调频性能已发生较大变化。文献[7]针对常规模型辨识要求初始与结束状态必须达到稳态的问题，提出了一种全局搜索能力更优的改进群优化算法。分析表明在深度调峰状态下一次调频能力与常规负荷条件下相比调频裕度变大。文献[8]针对火电机组进行深度调峰的一次调频性能与经济性之间的矛盾，提出一次调频优化控制策略，该策略较好地兼顾了两者，但未考虑机组的二次调频。文献[9]在简化的系统负荷频率控制（LFC）模型上采用灰狼优化（GWO）算法结合PID 控制器取得了较好的控制性能，但未考虑区域内多机组的出力分配情况。文献[10]针对互联水电系统负荷频率控制问题，提出基于Ziegler-Nichols 优化算法的改进PID 控制方法，为区域互联电网的稳定运行提供了新的研究思路。李嘉文等在综合能源系统经济调度框架下，建立了自动发电控制（AGC）指令动态分配的数学模型，提出了一种改进的深度确定性梯度算法，在LFC 模型中得到较好应用[11]。文献[12]针对多区域互联电力系统提出了一种鲁棒分布式预测控制算法，实现了负荷扰动下四区域互联电力系统的频率偏差稳定。上述文献虽然考虑了互联电力系统在扰动下的频率稳定性和AGC 发电功率指令的动态优化分配，但均未定量分析在经济性的前提下系统中实际机组有功出力分配情况。

对此，本文在火电机组参与深度调峰的背景下，将一次调频和二次调频结合起来，建立包含负荷频率控制和机组出力分配的互联电力系统模型，考虑了二次调频性能的火电机组负荷优化分配，兼顾整个火电机组的控制流程。仿真结果验证了本文所提算法优化后的PID 控制器不仅有效缩短频率波动范围，明显减少了振荡次数，而且在应对系统参数不确定性时具有较强的鲁棒性。

1 电网AGC 系统特性分析及动态建模

1.1 电网AGC 系统结构模型

经典的两区域互联电力系统主要包括调速器、控制器、原动机和发电机及负荷等环节，联络线作为各个区域之间功率流动渠道。首先考虑单区域-单机组AGC 整体模型（图1），用简化的低阶传递函数来表示各个环节。图1 中，Bi和Ri分别为该机组的频率偏差系数和调差系数。负荷扰动发生时，补偿系统功率失衡通过控制机组的有功出力实现。

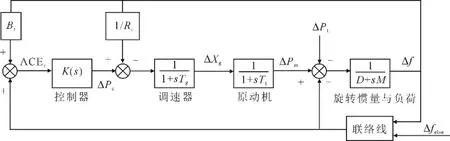
图1 单区域单机组AGC 整体模型Fig.1 The AGC overall model of single area single unit

1.2 发电机-电力系统模型

同步发电机的运动方程为

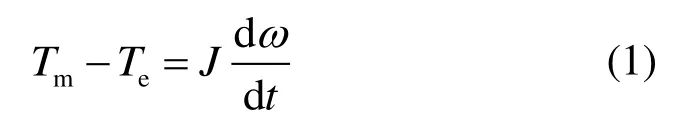
式中：Tm和Te分别为发电机的机械力矩和电磁力矩，J为转子的转动惯量。

根据力矩和功率之间的关系：P=ωT，再对式(1)进行拉普拉斯变换，可得到发电机功率平衡方程为

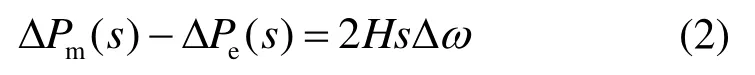
式中ΔPm和ΔPe分别为汽轮机机械功率及发电机电磁功率。

由于发电机的电磁功率受到负荷扰动和频率偏差的共同影响，所以有

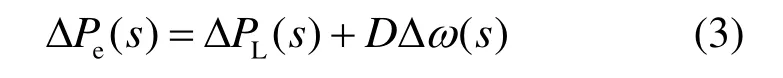
式中ΔPL为系统中接入的负荷扰动量。

将式(3)代入式(2)，可以得到

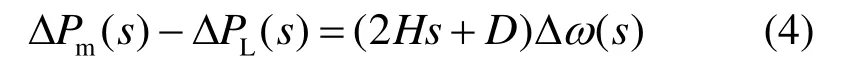
进一步可以得到考虑负荷扰动时的发电机-电力系统模型的一阶线性传递函数H(s)，即

式中，Δf为系统频率相对额定值的偏移量，D为系统负荷阻尼系数，M为机组转动惯量。

1.3 汽轮机模型

火电机组发电时利用汽轮机产生机械功率进一步使得发电机组发电。针对汽轮机，其汽阀位置的改变会引起进汽量的改变，进一步使得汽轮机的输出功率产生偏移。由于机械功率变化量往往滞后于阀门开度变化量，故常用一阶惯性环节来表示汽轮机的输入输出关系，有

式中：ΔPm为汽轮机输出功率偏移量，Tt为火电机组时间常数。

1.4 调速器模型

调速器是电网AGC 系统中最基本的控制元件，而火电机组中的汽轮机调速系统只有硬反馈。通常采用的调速器上搭载有液压装置，其数学模型可用传递函数W(s)表示为

式中，ΔXg为调速器位置增量，ΔPc为一次调频和二次调频综合作用下系统的控制偏差信号，Tg为涡轮机时间常数。

在单区域单机组AGC 整体模型中，经一次调频和二次调频综合作用下得到的ΔPc，可以表示为

式中，ΔP(s)为实时调度系统对机组的出力调节指令值，R为频率偏差系数。

第i个机组调速器在s域的传递函数如图2所示。

图2 机组i 的调速器传递函数示意Fig.2 Schematic diagram of the governor transfer function of unit i

1.5 联络线模型

互联电力系统中，控制区域之间通过高压输电线或联络线互联，每一个单独区域的频率变化都会影响与之互联区域的频率。两区域互联电网中AGC系统有功功率偏差是通过对各区域角速度偏差积分得到的，联络线有功功率增量方程为

式中，ΔωⅠ和ΔωⅡ分别为区域Ⅰ和区域Ⅱ的角速度偏差，XT为两区域之间的联络线阻抗。

进一步对联络线有功功率增量方程进行拉普拉斯变换可得到联络线一阶线性传递函数方程M(s)为

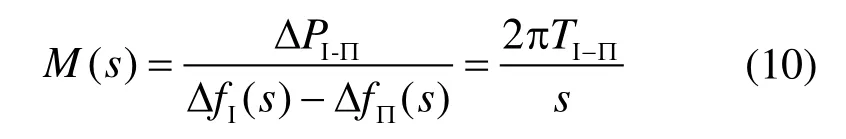
式中，ΔPⅠ-Ⅱ为联络线有功功率偏差，TⅠ-Ⅱ为联络线功率同步系数。

区域Ⅰ和区域Ⅱ之间的联络线在s域的传递函数如图3所示。

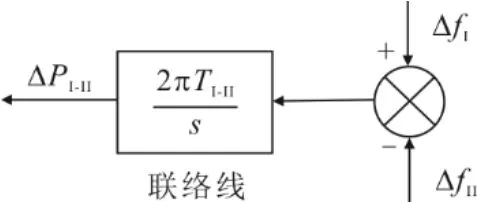
图3 联络线传递函数示意Fig.3 Schematic diagram of the tie line transfer function

以上模型都是基于线性化模型分析方法，因此可用于负荷扰动后电力系统频率动态计算。以后涉及单区域多机组以及多区域多机组的动态模型都根据单区域-单机组模型组合形成。

2 PID 参数优化对AGC 系统的影响

2.1 两区域互联电力系统

两区域互联电力系统模型如图4所示，其中火电机组内部单元包括发电机、调速器和汽轮机。区域Ⅰ中火电机组有3 台发电机，每台机组都有对应的分配系数，采用等效模型来简化发电机-负荷模型，为表征电网实际机组特性不同，同时在惯性环节设置参数差异；区域Ⅱ只有1 台发电机，通过联络线将区域Ⅰ和区域Ⅱ连接起来。两区域互联电网的网络结构和相关参数见文献[13-14]，仅在PID 控制器上有所不同。

图4 两区域互联电力系统模型Fig.4 The two-region interconnected power system

图4 为区域Ⅰ和区域Ⅱ互联的AGC 系统，针对每个区域而言保证该区域的频率处于正常水平是首要的。当发生扰动时其中一区域调节容量不足时，另外一区域可由联络线对该区域提供功率支撑。由功率平衡关系可得

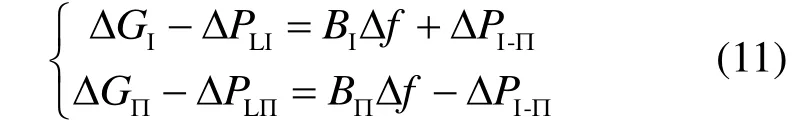
式中：ΔGⅠ和ΔGⅡ分别表示Ⅰ、Ⅱ区域各发电机组的发电功率变化值之和；ΔPLI和ΔPLII分别表示两区域接入的负荷扰动；BI和BII分别表示区域Ⅰ和区域Ⅱ的频率偏差系数；ΔPI-II表示区域Ⅰ对区域Ⅱ功率支撑值的大小，即两区域通过联络线交换的功率偏差；Δf为系统频率的偏移量，由于两系统通过联络线相互联接，因此频率变化值大小相等。

根据式(11)可以解得

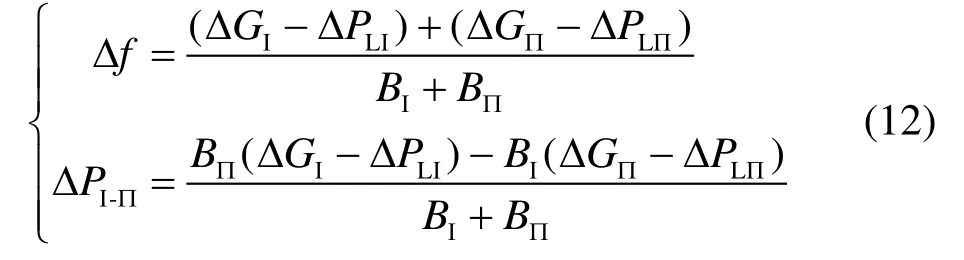
为使处于负荷扰动下的两区域电网对系统频率和联络线交换功率双重偏差做出快速动态响应，必须对区域控制误差ACE 的动态响应过程进行分析。两区域均采用联络线功率频率偏差控制（TBC）方式，区域Ⅰ和区域Ⅱ的ACE 计算公式为

2.2 PID 控制器

在控制器部分，经典PID 控制器的结构和算法在实际中被广泛应用。本文采用并联PID 控制规律，其中的积分调节器可达到无差调节[15]。其改变机组功率是借助频率偏差对时间的积分控制来实现的。在该调节方式下进行控制，机组功率的变化量ΔPg与系统频率偏差Δf积分量的大小相关，可表示为

由以上部分可得到PID 控制系统原理如图5所示。

图5 PID 控制系统原理Fig.5 The principle of PID control system

由PID 控制系统原理可以得到PID 控制器的传递函数，其表达式为

式中KP、KI、KD分别为控制器的比例、积分和微分系数。在控制器上若找到合适的PID 参数，电网的频率控制将达到更好的效果[16]。

2.3 基于改进Ziegler-Nichols 算法的PID 参数设计

Ziegler-Nichols 算法中的PID 整定方法在各种过程控制系统中有着广泛的应用。该算法通过比例控制器的临界振荡试验获取过程对象重要的临界频率响应特性，这是该频率响应方法的基本思路，并提供了相应的PID 参数整定规则。由于该整定方法不需要建立任何对象模型，并且简单实用，所以被广泛应用于控制领域中。

文献[10]提出的自适应PID 控制是在控制回路正常运行中完成的，不用切换到其他试验状态。在现有控制回路中进行调试，获得正常运行时的输入输出数据，然后批量进行处理，最终获得过程对象重要的临界频率响应特性，然后根据相应的PID 参数整定规则在线更新PID 控制器参数。这种自适应PID 控制能使控制回路始终保持在最佳运行状态，对负荷扰动后的电力系统恢复频率稳定具有一定的工程意义。

通过前文获得的临界频率ωs和频率响应特性G(jωs)，则可直接获得临界增益ku和临界周期Tu，分别为：

由于PID 控制器的传递函数已给出，故基于Ziegler-Nichols 算法的PID 整定规则见表1。改进的Ziegler-Nichols 算法是通过把过程对象奈奎斯特图闭环系统的Gk(jω)曲线上的临界点G(jωs)移到幅值为Am、相位为(−π+ψm)的点上，进而更新PID 参数。

表1 Ziegler-Nichols 算法PID 整定规则Tab.1 PID tuning rules of the Ziegler-Nichols algorithm

采用这种方法的优势是在某种程度上既满足了幅值裕度的要求，又满足了相位裕度的要求，改进后的PID 整定公式为：

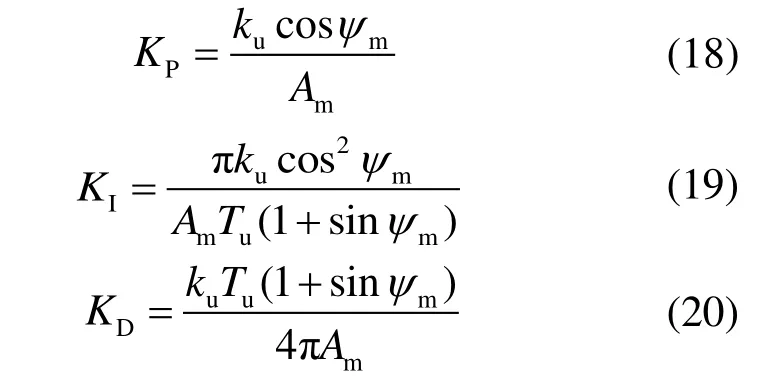
式中：Am一般取为2；ψm取π/9，可保证控制取得最佳效果。

本文采用改进的Ziegler-Nichols 优化算法对PID 参数进行整定，并对整定后的结果进行适当调整，最后得到其整定值：KP=0.601 4，KI=1.300 9，KD=0.097 8。

2.4 机组出力系数的确定

由于区域Ⅰ中有3 台机组，因此在研究AGC容量分配问题时，需要确定每台机组的出力分配系数。考虑二次调频能力的机组负荷优化分配时，通常以总煤耗量最低为目标进行优化，进一步确定区域Ⅰ各AGC 机组的调节容量。可得到机组发电所需煤耗量的目标函数为

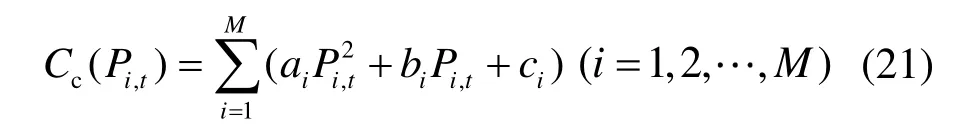
式中：Cc(Pi,t)表示火电机组在不同功率时的煤耗量；Pi,t为第i台火电机组自身的基准功率Pei和调节功率ΔPki之和，表示第i台机组的当前功率；M表示参与电网调频调峰的火电机组总数；ai、bi和ci分别表示各火电机组的煤耗量系数。

功率平衡约束和机组出力约束条件分别为：

式中：ΔPk为区域Ⅰ所有火电机组承担的总的AGC调节功率，Pi,min为第i台机组的最低出力，Pi,max为第i台机组的最高出力。

将火电机组的煤耗量目标函数最小化，可得到各机组的最优出力组合[h1,h2,…,hM]，进一步等比例设置各AGC 机组的出力分配系数为[d1,d2,…,dM]，则机组出力系数的计算公式为

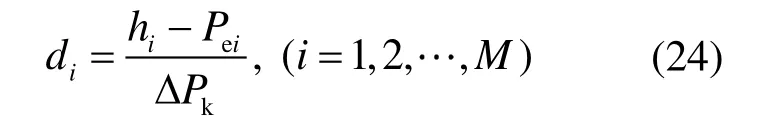
互联电力系统的初始参数见表2。

3 算例分析

3.1 负荷扰动仿真验证

为了验证经改进Ziegler-Nichols 算法（改进Z-W）优化后的PID 控制器应用于区域互联电网的有效性，建立两区域互联电力系统模型。针对不同地域的电网而言，采取区域调节责任分配方式能有效降低其他区域火电机组有功出力的次数，进而降低机组的损耗成本。该分配方式通过设置火电机组的调差系数1/Ri和频率偏差系数Bi相等[17-18]，从而实现各区域对其扰动的平衡。

按照式(18)—式(21)的经济分配方式对区域Ⅰ的各机组出力进行分配[19]，机组经济性分配结果如图6所示。

图6 表示用优化算法进行迭代寻优找到保证消耗煤炭量最小的区域Ⅰ机组出力最优分配系数，同时也能得到对应消耗煤炭总量的最小值，图6 显示出算法的具体迭代过程；与之进行对比的3 台机组平均分配出力得到的总煤耗量，是通过公式(21)和表2 计算得到。从图6 可见，利用经济分配方法的区域Ⅰ机组消耗的煤炭总量为414.207 t，而与此同时区域Ⅰ所有机组进行平均分配的前提下消耗的煤炭总量为421.433 t，因此该分配方法有效地节省了煤耗，给电网带来可观的经济效益。

进一步分析，设置10 s 区域Ⅰ发生负荷扰动ΔPL1=0.2 p.u.，区域Ⅰ发电机额定容量P=1 000 MW，区域Ⅰ负荷功率的基准值为1 000 MW，因此需要额外的AGC 调节功率为200 MW。考虑分配系数的互联电网频率控制策略的经济性最优分配结果：[d1d2d3]=[0.031 0.548 0.421]。在该分配方法下，基于两区域系统仿真模型，分别使用传统的PI 控制、经PSO 算法优化后的PID 控制器和经改进Ziegler-Nichols 算法优化的PID 控制器进行仿真验证。不同PID 参数下AGC 系统5 个输出量的动态变化过程分别如图7—图9所示。

从图7—图9 中可以看出，利用同样的经济分配方法设置机组出力系数时，PID 参数整定前后AGC 系统5 个输出量在多个动态性能指标上存在显著变化，尤其在偏移程度和响应时间上。如在同样的出力分配系数组合下，分析不同PID 参数下区域Ⅰ的频率偏差Δf1，经改进Ziegler-Nichols 算法优化后的PID 控制的频率偏差Δf1比PSO 优化的PID控制和传统的PI 控制下Δf1振荡幅度更小，调节时间更短，能使系统频率更快趋于稳定值。从而验证了经改进Ziegler-Nichols 算法优化得到的PID 控制器对调节互联AGC 系统频率的控制效果更好，具有更好的时域响应特性。

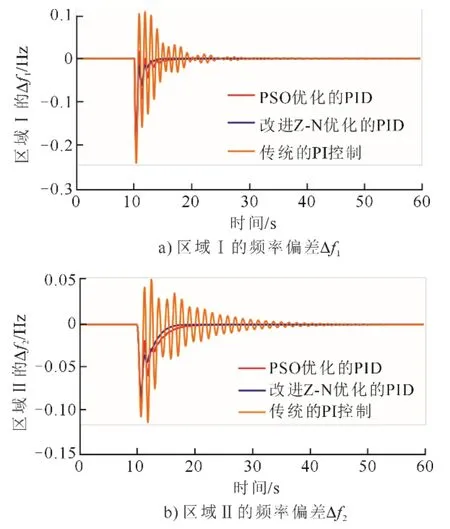
图8 不同PID 参数下系统频率偏差动态响应曲线Fig.8 The dynamic response curves of system frequency deviation with different PID parameters

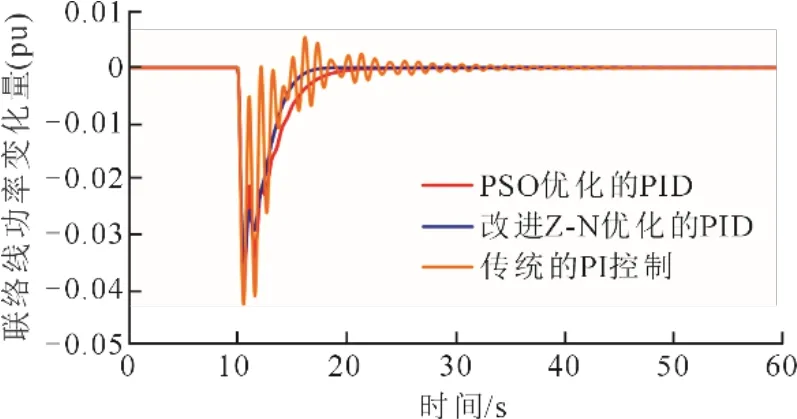
图9 不同PID 参数下联络线动态响应曲线Fig.9 The dynamic response curves of tie line with different PID parameters

当区域Ⅰ发生扰动ΔPL1=0.2 pu 时，图10 表示在改进Ziegler-Nichols 算法优化的PID 控制下，互联电力系统的AGC 调节容量的动态响应过程。

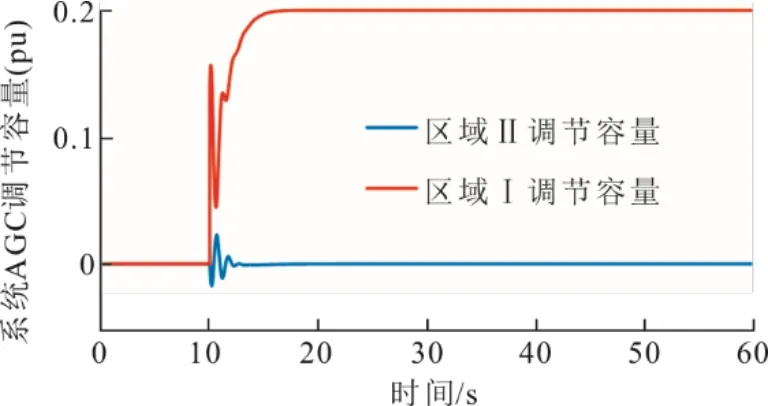
图10 区域Ⅰ和区域Ⅱ的调节容量响应曲线Fig.10 The regulated capacity response curves of zone I and zone II

分析图10 中系统总调节功率ΔPk变化过程，区域Ⅰ的机组调节功率ΔPk1最终稳定在0.2 pu，与此同时，区域Ⅱ的机组调节功率ΔPk2稳定值为0。进一步证明了出现扰动的区域Ⅰ火电机组动作，而无扰动的区域Ⅱ机组不发生动作，避免了无扰动区域火电机组的频繁启停，降低了机组的损耗成本。

3.2 控制器鲁棒性分析

当两区域AGC 系统的参数变化时，采用改进Ziegler-Nichols 算法的PID 控制对互联电力系统的鲁棒性进行分析。规定整个系统的汽轮机时间常数Tt相对其基准值依次在–40%～40%范围内改变20%，联络线功率同步系数TI-II依理同上。图11 和图12 分别为系统区域Ⅰ产生0.1 pu 的负荷阶跃扰动时，汽轮机时间常数Tt和联络线功率同步系数TI-II变化时区域Ⅰ频率偏移的仿真结果。

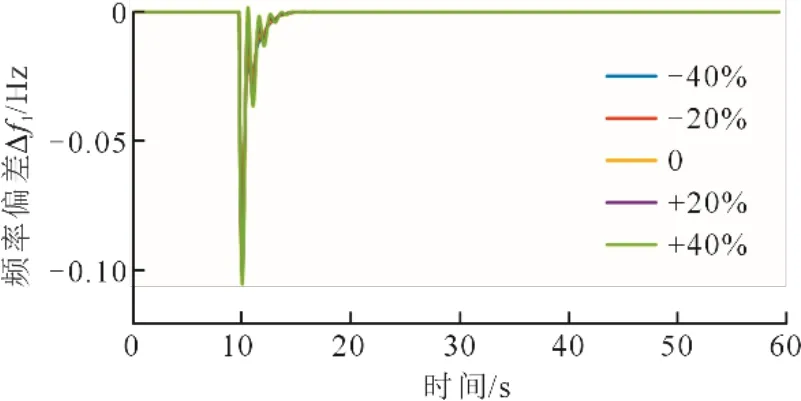
图11 不同汽轮机时间常数Tt 下频率偏差Δf1 的变化Fig.11 Variations of frequency deviation Δf1 with different steam turbine time constants Tt

图12 不同联络线功率同步系数TI-II 下频率偏差Δf1 的变化Fig.12 Variations of frequency deviation Δf1 with different tie-line power synchronization coefficients TI-II

由图11 和图12 可见，当AGC 机组汽轮机时间常数和联络线功率同步系数发生改变时，在10 s对区域Ⅰ施加0.1 pu 的负荷阶跃扰动，本文提出的改进Ziegler-Nichols 算法优化后的PID 控制器能使得区域Ⅰ的频率偏差Δf1在扰动发生后6 s 左右趋近于0。系统频率偏差Δf1能快速消除，并且Δf1的超调量较小，在误差允许范围内。从而验证了本文设计的PID 控制器能抵御系统参数变化的影响，对于电网火电机组自身特性参数发生变化时能很好地适应，具有较好的鲁棒性。电网工作环境中存在种种不确定性，火电机组参数变化后系统频率能迅速恢复到额定值，这对于延长扰动区域AGC 机组的使用寿命有着重要的意义。

4 结论

1）基于火电机组参与深度调峰的背景下，建立了单区域多机组和单区域单机组的两区域互联电力系统负荷频率控制模型，提出考虑二次调频能力的火电机组负荷优化分配策略，并引入了改进的Ziegler-Nichols 优化算法。

2）针对互联电力系统的频率稳定问题提出一种改进Ziegler-Nichols 算法的PID 控制方法，为使处于负荷扰动下的两区域电网做出快速动态响应，对其进行优化后的PID 控制，旨在快速恢复电网平稳运行。

3）通过设置相关的出力分配系数，结合火电机组的经济调度和自动发电控制于一体，对于四机两区域系统较为适用，同时也可以应用到多区域多机组的互联电力系统中。

4）采用改进Ziegler-Nichols 算法优化得到的PID 控制器比以往其他传统的PID 控制方法具有更佳的控制效果，在不同的负荷扰动下系统仍有较好的动态性能；并且系统参数发生改变的情况下，本文算法优化后的PID 控制器具有较强的鲁棒性，能适应不同机组的调峰调频功能。