双尺度小火焰模型预测混合层火焰中PAHs的生成

蔡瑞鹏，罗 坤，金 台，樊建人

双尺度小火焰模型预测混合层火焰中PAHs的生成

蔡瑞鹏1，罗 坤1，金 台2，樊建人1

(1. 浙江大学能源清洁利用国家重点实验室，杭州 310027；2. 浙江大学航空航天学院，杭州 310027)

本文验证了双尺度过程变量小火焰方法在层流混合层火焰中的适用性，该方法通过增加额外的过程变量PAHs来提高传统过程变量小火焰方法对多环芳烃的预测能力．通过与直接数值模拟结果的先验和后验对比，证明了该方法的优越性．在后验验证中，由于对过程变量PAHs源项的偏低预测继而导致了对多环芳烃组分峰值的预测偏低．通过分析直接数值模拟结果中的小火焰分支，推测过程变量PAHs源项的偏低预测是小火焰的多维性造成的．

双尺度；过程变量；小火焰模型；多环芳烃

众所周知，多环芳烃(polycyclic aromatic hydrocarbons，PAHs)具有很强的致癌和致突变特性，对环境和人类健康有很大危害．同时，PAHs也是碳烟生成的重要前驱物．因此，需要研究燃烧过程中PAHs的生成特征，从而更好地控制PAHs和碳烟的生成．数值模拟方法能够提供燃烧过程中PAHs生成的详细信息，但是需要耦合非常详细的化学反应机理(通常包含几百种组分和几千步反应)，极大地增加了计算成本．小火焰模型能够把化学反应的求解从流场的求解中解耦，极大地降低计算量．因此，使用小火焰模型预测燃烧过程中PAHs的生成具有很大的前景．

目前，已有一些研究使用小火焰模型预测PAHs的生成．Verhoeven等[1]使用小火焰生成流形(flamelet generated manifold，FGM)方法[2]预测了层流CH4伴随流火焰中PAHs的生成．模拟和实验结果的对比表明，PAHs生成的主要特征可以被预测，但是最大PAHs浓度的位置不能被很好预测．Mueller和Pitsch[3]模拟了天然气湍流非预混火焰中碳烟的生成，且使用小火焰/过程变量(flamelet/progress variable，FPV)方法[4]预测PAHs的生成．在该FPV方法中，求解总包PAH的输运方程，从小火焰库中插值得到该输运方程的源项，并使用求解得到的PAH质量分数对负源项进行修正．结果表明，尽管模拟与实验数据较吻合，但PAHs和碳烟的预测仍有很大提升空间．Xuan和Blanquart[5]发展了一个新的松弛方法来计算PAHs输运方程的源项，其不仅对负源项进行修正，也对正源项进行修正．他们使用该方法预测了乙烯湍流非预混合火焰中PAHs和碳烟的生成[6]，模拟结果证明了该方法的准确性．但是，如果采用该方法预测较多PAHs组分，则需要求解非常多的PAHs输运方程，从而大幅度增加复杂性和计算成本．

在之前的工作中，笔者发展了一种双尺度过程变量小火焰(dual-scale flamelet/progress variable，DS-FPV)方法[7]，其能够显著提高传统FPV方法[8]预测PAHs生成的能力，且复杂性和计算成本并无较大增加．在该方法中，考虑到化学反应的多尺度性质，定义了额外的过程变量PAHs来描述燃烧过程中PAHs的生成．发展的DS-FPV方法通过与详细化学(detailed chemistry，DC)模拟进行对比，被证明可以准确预测PAHs的生成．目前，该方法仅在相对简单的对冲火焰中进行了验证，考虑到实际燃烧器相对复杂的几何结构，其适用性有待验证．本文将在混合层火焰中进一步验证DS-FPV方法的性能．

1 数值方法

1.1 DC模拟

在DC模拟中，直接求解质量、动量、总焓和组分质量分数的控制方程以及气体状态方程，所求解方程的具体表达式可参考文献[7]．

考虑到本文的研究后续将扩展到煤粉燃烧的PAHs生成研究中，为了保证DS-FPV方法的可扩展性，采用的燃料为挥发分组分混合物．挥发分中含有的组分为：H2(0.84%)，H2O(10.92%)，CO(6.37%)，CO2(4.06%)，CH4(9.68%)，C2H4(2.51%)，C2H6(2.51%)，C3H6(2.51%)，C3H8(1.25%)和C6H6(59.34%)[9]，各组分所占百分比为质量百分比．本文采用Richter和Howard发展的经过广泛验证的芳香烃化学反应机理(158种组分和872步反应)[10]．本文主要研究4种具有代表性的PAHs组分，即苊(A2R5H2)，苊烯(A2R5)，蒽(A3)和菲(A3L)．考虑到采用详细化学反应机理的计算成本非常大，本文对二维混合层火焰进行模拟，算例的设置如图1所示．计算域的长和宽分别为80mm和40mm．燃料从计算域底部右侧喷入，空气从计算域底部左侧喷出，入口速度的大小均为1m/s．燃料和空气喷口的长度分别为15mm和25mm．在轴和轴方向的网格结点数为160×160，且均为拉伸网格．在轴方向，＝25mm附近区域的网格最小；在轴方向，入口处网格最小．在整个计算域中，最小网格尺寸为0.017mm，最大网格尺寸为0.8mm．DC模拟在开源软件平台OpenFOAM-v6[11]上进行，使用reactingFoam求解器，计算时长约38000CPUh．

图1 混合层算例设置示意

1.2 DS-FPV

小火焰模型假设流场中组分和热量的扩散主要沿着混合分数梯度方向，在混合分数等值面内组分和热量的扩散可以忽略不计，因此流场中组分和温度的分布满足一维假设(混合分数空间)，即流场中的火焰可以看作一维小火焰单元的集合．因此小火焰模型可以事先求解不同标量耗散率下的小火焰单元，将化学反应的求解从流场的求解中解耦，从而极大地降低使用详细化学反应机理带来的巨大计算量．如前文所述，传统的FPV方法不能准确预测燃烧过程中PAHs的生成，而DS-FPV方法能够提高传统FPV方法对PAHs生成的预测准确度，两种方法的不同点在于DS-FPV方法使用两个过程变量和PAHs来分别描述流场中主要组分和温度的演化以及PAHs的演化．DS-FPV方法的操作流程如下．首先，使用FlameMaster[12]求解不同当量标量耗散率下的小火焰方程．然后，将得到的小火焰解分别映射到参数变量混合分数和过程变量以及和过程变量PAHs上，即生成小火焰库＝(，)和＝(，PAHs)．其中，过程变量为组分CO2，H2O，CO和H2的质量分数之和，过程变量PAHs为组分A2R5和A3的质量分数之和．过程变量PAHs的定义过程如下：选择所研究PAHs组分中的任意两种的质量分数之和作为过程变量PAHs，结果发现A2R5和A3的组合能够准确地预测PAHs组分的生成．从化学反应机理的角度分析，这可能是因为A2R5和A2R5H2的生成密切相关，而A3和A3L的生成密切相关，故而A2R5和A3的演化能够很好地代表所研究PAHs的演化．最后，求解参数变量混合分数，过程变量和过程变量PAHs的输运方程，所求解方程的具体表达式可参考文献[7]．求解上述方程过程中，需使用参数变量，和PAHs在小火焰库中插值得到相关变量值，对于主要组分和温度，＝(，)；对于PAHs，＝(，PAHs)．在本文中，小火焰库(，)和(，PAHs)的大小均为101×85．

为了全面评价DS-FPV方法的性能，首先进行先验分析．在先验中，小火焰库参数变量混合分数、过程变量和过程变量PAHs直接从DC结果中得到．然后根据，和PAHs在小火焰库中插值得到所需热物理量，并将其与DC结果进行比较，来验证小火焰库的准确性．其次，进行后验分析．在后验中，小火焰库参数变量混合分数、过程变量和过程变量PAHs通过求解其输运方程得到，并使用求解得到的，和PAHs在小火焰库中插值得到所需热物理量．将后验模拟结果与DC结果进行比较来进一步验证DS-FPV方法的准确性．DS-FPV模拟在基于reactingFoam求解器开发的求解器DSFPVFoam上进行．DC和DS-FPV模拟所用的求解器，除燃烧模块外，其他模块代码均相同，且速度和压力的耦合算法均采用PIMPLE算法．DS-FPV模拟所需时间约为120CPUh．DC和DS-FPV模拟所需CPUh差异巨大，是因为DC模拟花费大量时间来计算化学反应的积分源项(158种组分和872步反应)，而DS-FPV方法将化学反应与流动解耦，可以事先计算化学反应，继而极大程度地降低计算成本．

2 结果与讨论

2.1 小火焰方程分析

图2是DC模拟结果温度的云图．图中绿色实线为混合分数梯度的流线，即每条绿色实线表示一个小火焰分支，每条小火焰分支左侧和右侧端点混合分数的值分别为0和1；图中红色实线为组分A3质量分数的等值线，靠近燃料和空气入口等值线的值较小，4条等值线的值从下往上依次是0.00024、0.00072、0.00120和0.00168．从图中可以看出，A3生成的区域在靠近火焰中心的富燃侧，且其他PAHs组分的分布规律和A3类似(图中未展示)．PAHs组分的分布规律说明了采用两个过程变量和PAHs来扩展传统FPV方法的必要性．两个过程变量的作用分别为：过程变量来描述高温区中主要组分的变化，即CO2，H2O，CO和H2的变化，且这些组分通常包含在传统过程变量的定义中；过程变量PAHs用来描述靠近高温区富燃侧PAHs的变化，在该区域内过程变量的变化较小故不适合作为描述PAHs变化的特征量．另一方面，从图中也可以看出，绿线和红线在流场中的绝大部分区域相互垂直，这说明A3的扩散主要沿着混合分数梯度方向.其他PAHs的等值线，如A3L、A2R5和A2R5H2，同样在大部分区域与混合分数梯度方向垂直(图中无显示)，定性证明了流场中PAHs的输运满足一维假设.

图2 DC模拟结果温度T的分布云图

为了从定量上说明流场中PAHs的输运满足一维假设，对图2中的小火焰分支进行分析．在刘易斯数等于1的假设下各组分的一维稳态小火焰方程可以表示为

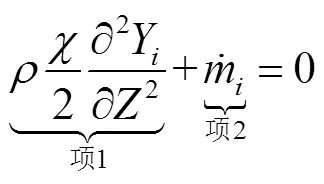
式中：c是标量耗散率，其表示燃烧偏离稳定状态的程度[13]；是化学反应引起的源项；r是气体密度；Yi是组分i的质量分数．图3为主要组分(H2O，CO2，H2和CO)和PAHs组分(A2R5，A3，A2R5H2和A3L)的一维稳态小火焰方程分析结果，其中“项1”表示小火焰方程(1)中的第一项，“项2”表示小火焰方程(1)中的第二项，“总和”表示“项1”和“项2”之和，“零”表示纵坐标为0的参考线．从图中可以看出不管是对于主要组分(图3中第一列)还是PAHs组分(图3中第二列)，其在流场中的输运均可用近似用一维稳态小火焰方程(1)描述，虽然黑色实线和黑色虚线之间在某些区域存在偏差．这些偏差的出现可能是由小火焰的多维性引起的，文献[14-15]指出当流场中混合分数等值线和组分浓度等值线不平行程度增大时，小火焰的多维性将变得显著．图2中组分浓度等值线的拐点附近与混合分数梯度不垂直，即与混合分数等值线不平行，此处小火焰的多维性造成了图3中的偏差．综上所述，在定量和定性上均证明了流场中不管是主要组分还是PAHs组分的输运均近似满足一维小火焰方程．

2.2 DS-FPV方法先验分析

图4为4种PAHs组分A2R5，A3，A2R5H2和A3L质量分数的FPV，DS-FPV先验结果与DC模拟结果的对比，第一列为计算域高度＝30mm处的结果，第二列为计算域高度＝70mm处的结果．先验分析的目的是验证所选小火焰库参数的合理性，检验过程变量PAHs是否能够准确地描述PAHs组分的变化．从图4中可以看出，相比于传统的FPV方法，由于DS-FPV方法使用了额外的过程变量PAHs，其能够很好地预测PAHs的生成．为了保证DS-FPV方法在后验中能够准确地预测PAHs的生成，过程变量PAHs的源项也需在先验中被准确预测．图5为过程变量源项PAHs(即A2R5和A3的源项之和)的FPV，DS-FPV先验结果与DC结果的对比，第一行为计算域高度＝30mm处的结果，第二行为计算域高度＝70mm处的结果．从图中可以看出，对于组分A2R5的源项，DS-FPV与FPV相比更接近DC的结果．且FPV结果在部分区域与DC结果相比偏差较大，与之前对冲火焰[7]中FPV与DC结果较吻合的情况相反．这说明在本质上过程变量PAHs更适合描述其源项的变化，虽然对于组分A3的源项，FPV优于DS-FPV的先验结果．

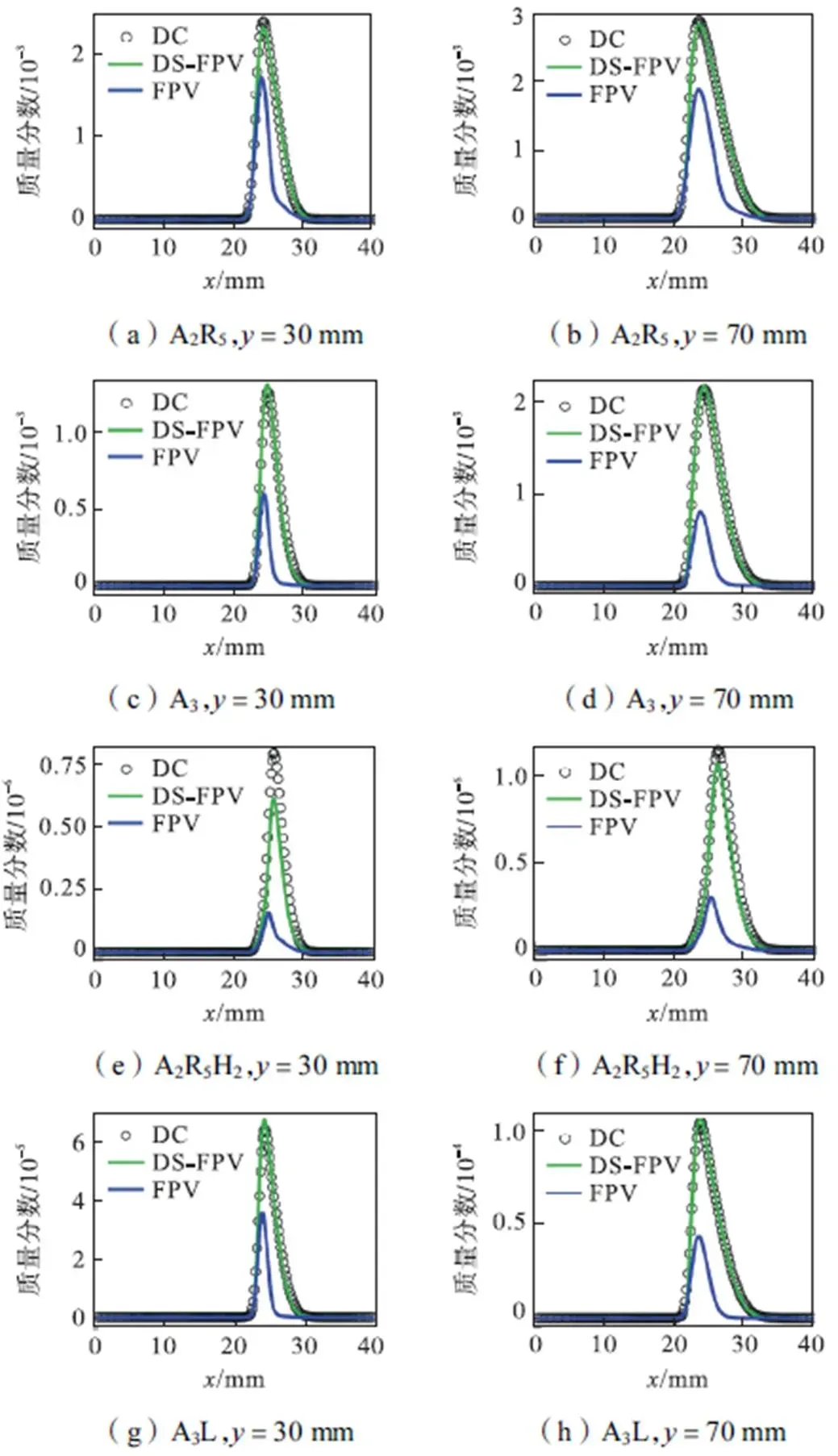
图4 A2R5，A3，A2R5H2和A3L质量分数的FPV和DS-FPV先验结果与DC模拟结果的对比

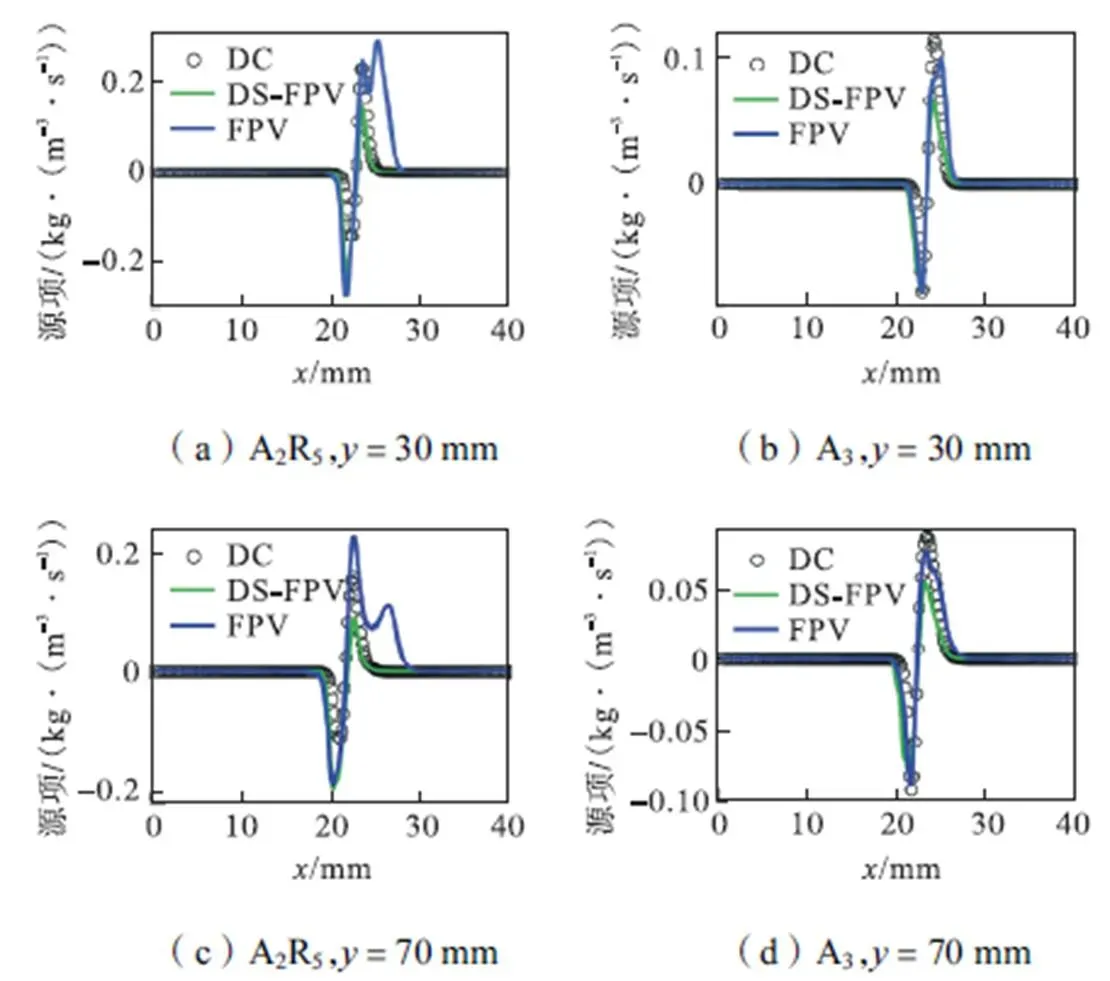
图5 A2R5和A3源项FPV和DS-FPV先验结果与DC结果的对比

2.3 DS-FPV方法后验分析

图6为A2R5、A3、A2R5H2和A3L质量分数的DS-FPV后验结果与DC模拟结果的对比，第一列为计算域高度＝30mm处的结果，第二列为计算域高度＝70mm处的结果．从图中可以看出，DS-FPV方法均低估了A2R5、A3、A2R5H2和A3L的质量分数，这是由于过程变量PAHs的源项被低估，如图5所示．在先验分析中已证实FPV方法不能准确预测PAHs的生成，故在本小节中未进一步对FPV的后验结果进行分析．相比于对冲火焰[7]的结果，本文证明了DS-FPV方法在复杂构型中的适用性，虽然过程变量PAHs源项被偏低预测．在以后的工作中，将验证DS-FPV方法在湍流扩散火焰中的适用性，并与碳烟生成模型耦合预测碳烟的生成．

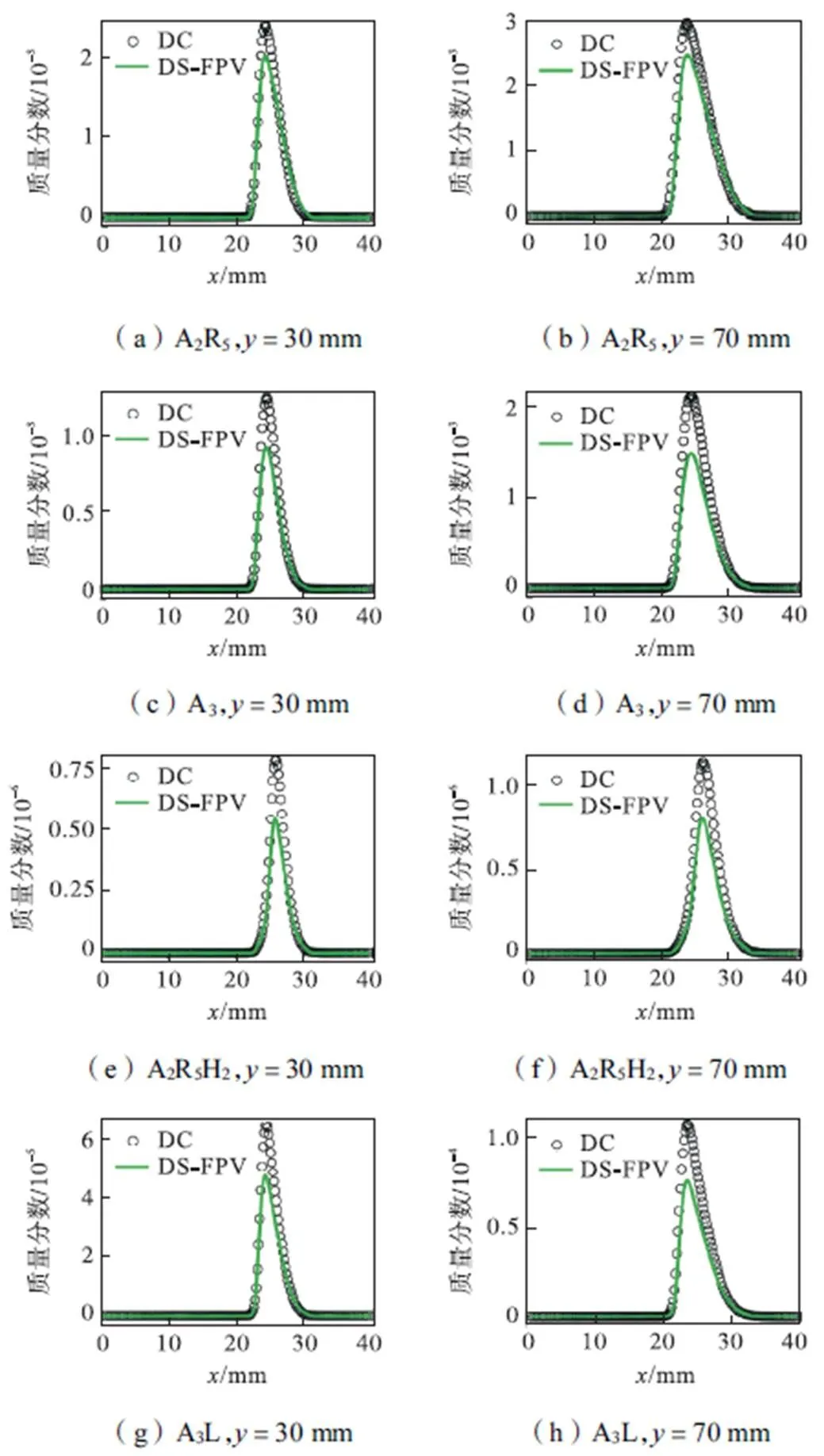
图6 A2R5、A3、A2R5H2和A3L质量分数的DS-FPV后验模拟结果与DC模拟结果的对比

3 结 论

本文将发展的DS-FPV方法应用到混合层火焰中，并通过与DC模拟结果的先验和后验对比，证明了该方法在复杂构型中的适用性．先验结果表明，增加过程变量PAHs的DS-FPV方法相对于传统的FPV方法，能够很好地预测混合层火焰中PAHs的生成．由于DS-FPV方法对过程变量PAHs源项的预测偏低，导致在后验结果中PAHs组分的峰值被偏低预测．通过分析DC结果中的小火焰分支，推测过程变量PAHs源项的偏低预测是小火焰的多维性造成的．

［1］ Verhoeven L M，de Andrade Oliveira M H，Lantz A，et al. A numerical and experimental study of polycyclic aromatic hydrocarbons in a laminar diffusion flame[J].，2013，34(1)：1819-1826.

［2］ van Oijen J A，Lammers F A，de Goey L P H. Modeling of complex premixed burner systems by using flamelet-generated manifolds[J].，2001，127(3)：2124-2134.

［3］ Mueller M E，Pitsch H. LES model for sooting turbulent nonpremixed flames[J].，2012，159(6)：2166-2180.

［4］ Ihme M，Pitsch H. Modeling of radiation and nitric oxide formation in turbulent nonpremixed flames using a flamelet/progress variable formulation[J].，2008，20(5)：055110.

［5］ Xuan Y，Blanquart G. A flamelet-basedanalysis on the chemistry tabulation of polycyclic aromatic hydrocarbons in non-premixed flames[J].，2014，161(6)：1516-1525.

［6］ Xuan Y，Blanquart G. Effects of aromatic chemistry-turbulence interactions on soot formation in a turbulent non-premixed flame[J].，2015，35(2)：1911-1919.

［7］ Cai R，Luo K，Gao Z，et al. Dual-scale flamelet/progress variable approach for prediction of polycyclic aromatic hydrocarbons formation under the condition of coal combustion[J].，2020，34(8)：10010-10018.

［8］ Pierce C D，Moin P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion[J].，2004，504：73-97.

［9］ Muto M，Yuasa K，Kurose R. Numerical simulation of ignition in pulverized coal combustion with detailed chemical reaction mechanism[J].，2017，190：136-144.

［10］ Richter H，Howard J B. Formation and consumption of single-ring aromatic hydrocarbons and their precursors in premixed acetylene，ethylene and benzene flames[J].，2002，4(11)：2038-2055.

［11］ Weller H G，Tabor G，Jasak H，et al. A tensorial approach to computational continuum mechanics using object-oriented techniques[J].，1998，12(6)：620-631.

［12］ Pitsch H. FlameMaster：A C++ Computer Program for 0D Combustion and 1D Laminar Flame Calculations[EB/OL]. https://web.stanford.edu/group/pitsch/ FlameMaster.htm，2020-07-17.

［13］ Claramunt K，Consul R，Carbonell D，et al. Analysis of the laminar flamelet concept for nonpremixed laminar flames[J].，2006，145(4)：845-862.

［14］ Xu H，Hunger F，Vascellari M，et al. A consistent flamelet formulation for a reacting char particle considering curvature effects[J].，2013，160(11)：2540-2558.

［15］ Scholtissek A，Chan W L，Xu H，et al. A multi-scale asymptotic scaling and regime analysis of flamelet equations including tangential diffusion effects for laminar and turbulent flames[J].，2015，162(4)：1507-1529.

Dual-Scale Flamelet Model for Prediction of PAHs Formation in Mixing Layer Flame

Cai Ruipeng1，Luo Kun1，Jin Tai2，Fan Jianren1

(1. State Key Laboratory of Clean Energy Utilization，Zhejiang University，Hangzhou 310027，China；2. School of Aeronautics and Astronautics，Zhejiang University，Hangzhou 310027，China)

In this paper，the applicability of the dual-scale flamelet/progress variable approach was verified in a combusting laminar mixing layer. In this approach，an additional progress variablePAHswas defined to improve the capability of the traditional flamelet/progress variable approach to predict the formation ofpolycyclic aromatic hydrocarbons(PAHs). This approach was validated by comparing with the detailed chemistry simulation. In theanalysis，the mass factions of PAHs are under-predicted due to the under-prediction of the source term ofPAHs. By analyzing the flamelet in the results of detailed chemistry simulation，it is concluded that the under-prediction of the source term ofPAHsis caused by the multi-dimensional effect of flamelet.

dual-scale；progress variable；flamelet model；polycyclic aromatic hydrocarbons

TK16

A

1006-8740(2021)05-0501-06

10.11715/rskxjs.R202108019

2021-03-04．

国家重点研发计划资助项目(2017YFB0601805).

蔡瑞鹏（1994—  ），男，博士研究生，crp@zju.edu.cn.

罗 坤，男，博士，教授，zjulk@zju.edu.cn.

(责任编辑：武立有)