一种用于车载变压器的局部放电高精度协同定位方法

贾步超， 梁爽， 郎光娅

(1.中车青岛四方机车车辆股份有限公司，山东 青岛 266111;2.西南交通大学 电气工程学院，四川 成都 611756)

0 引 言

随着我国铁路规模的扩大和车辆制造技术的提升，高速铁路动车组的里程数和城市覆盖率也在大幅提升[1]。车载变压器是动车组与牵引电力网的直接媒介，同时也是最主要的动力来源。车载变压器的寿命通常取决于绝缘状态[2]，若不能及时对其评估，绝缘一旦出现较大故障，将直接导致动车组动力来源中断，影响铁路系统的正常运行，因此及时对车载变压器绝缘状态进行诊断和评估是必需的。

局部放电是变压器绝缘劣化的主要原因，也是绝缘故障的主要症状。因此，对局部放电进行检测、分类和定位是评估变压器绝缘状态的关键。传统的局部放电测量方法可以协助判断变压器绝缘是否开始劣化，但不能估计局部放电源的位置。因而，定位局部放电源是绝缘故障诊断、评估和维修过程中至关重要的组成环节[3]。

关于局部放电源定位的研究大多是基于到达时差(TDOA)方法，即利用TDOA方法的信息建立一组超定方程，然后采用迭代方法求解。然而，采用迭代方法易陷入局部最优[4]，导致最终结果不收敛。因此，越来越多的非迭代算法被用于估计局部放电源的坐标[5-6]。除此之外，车载变压器的油箱结构以及测量噪声的影响也会阻碍变压器内部的局部放电源的准确定位。通过结合DE-PSO算法和牛顿法的优势对车载变压器内部的局部放电源进行协同定位，减弱了变压器油箱结构和噪声带来的影响，进一步提高了局部放电定位的精度，从而有效解决了车载变压器局部放电难以精确定位的问题。

1 声信号传播

如图1所示，由于声波的反射和沿油箱壁的传播，局部放电源与声发射传感器之间存在一条以上的声传播路径。由于沿箱壁传播的信号到达声发射传感器的速度可能比直接传播的信号快，如信号S3可能在信号S1之前到达声发射传感器1号，因此多径传播会影响声信号的到达时间，这会给定位带来相当大的误差。

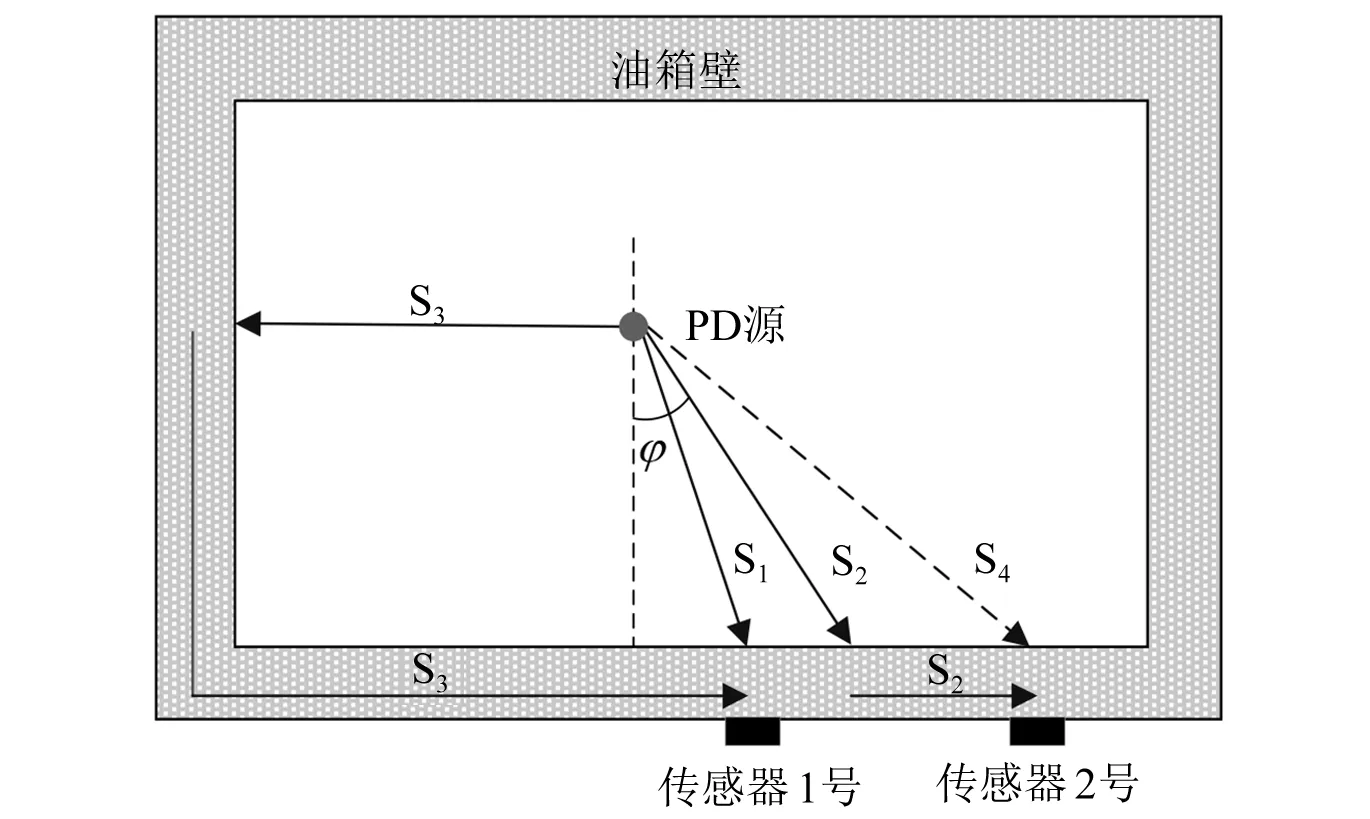
图1 声波传播过程

当来自绝缘油的声波以大于临界角的角度进入油箱壁时，会发生全反射。如果声发射传感器(例如传感器2号)没有位于全反射临界角的范围内，则声波无法直接从局部放电源(直线，如S4)传播到声发射传感器。但是，时间差方程仍然是用直线距离建立的，这给定位带来了很大的误差。

如果声发射传感器在全反射角以外，声信号会先在油中传播，并以全反射临界角射入油箱壁，再沿油箱壁传播至传感器，如图2所示。那么在定位计算中应该代入的距离(即为声信号传播的等效距离)为：

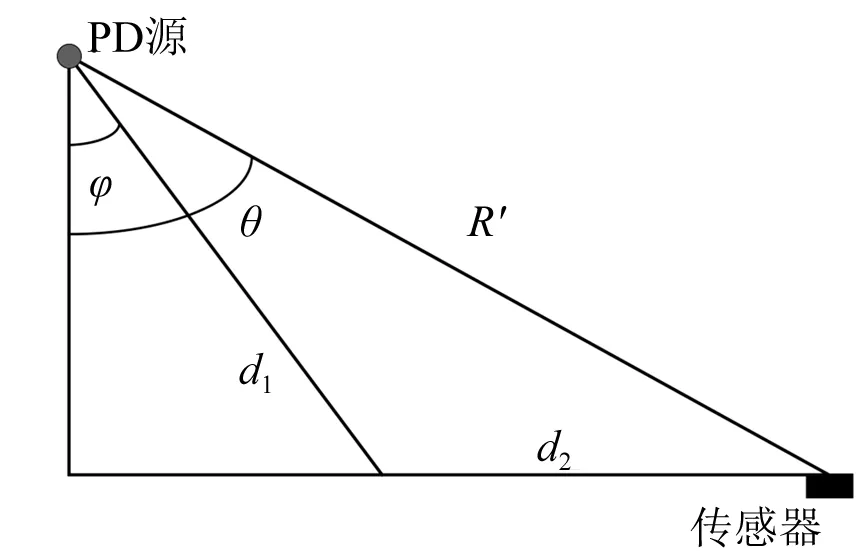
图2 声传播示意图

(1)

式中:θ和R′分别为局部放电源到传感器的角度和直线距离；φ为声信号在绝缘油中传播的实际路径所对应的角度；voil和vwall分别为声信号在绝缘油和油箱壁中的传播速度；R为声信号在绝缘油中传播了t时间后的距离，也是不考虑油箱壁的影响计算得到的局部放电源和传感器之间的直线距离。

2 DE-PSO算法协同定位

2.1 代价函数

在三维空间中，使用TDOA方法定位局部放电源需要至少4个传感器。本文设置4个传感器，并选择第1个传感器作为参考传感器。如果局部放电源的坐标设为p=[x,y,z]T，第i个传感器的坐标设为si=[xi,yi,zi]T，i= 1, 2, 3, 4，则局部放电源p与第i个传感器si之间的距离为：

(2)

那么到达距离差方程为：

(3)

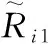
则约束代价函数为：

(4)

式中：w为权重矩阵,w=[BQBT]-1;B=diag(R2,R3,R4);Q为高斯噪声的协方差矩阵。

2.2 混合DE-PSO算法

粒子群(PSO)算法收敛速度快，可以有效解决复杂的优化问题，但是进化中的随机性使得其易陷入局部最优。当差分进化(DE)算法在优化迭代的后期接近最优解时，其收敛速度会变慢，从而很容易导致局部最优。因此，为了弥补DE算法和PSO算法的不足，并提高全局搜索能力，将DE算法与PSO算法结合形成混合DE-PSO算法。

DE-PSO算法首先使用DE算法的变异和交叉操作来扰动PSO粒子的当前位置，以增加种群的多样性并提高PSO的全局搜索能力，同时避免粒子陷入局部最优状态；此后，选择pibest和pgbest以更新所有粒子的速度和位置；然后依据每个个体的函数适应度值选择与最佳适应度值相对应的粒子进入下一次迭代，直到达到终止条件为止。图3为DE-PSO算法的流程图。

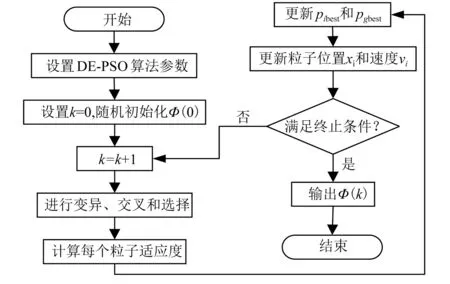
图3 DE-PSO算法流程图

2.3 协同定位

牛顿法可以有效地求解目标函数，但当其初始值选取不合适时，可能会导致最终定位失败。因此，通过使用DE-PSO算法可以得到初步的定位结果，然后将初步的定位结果作为牛顿法的初值，可以解决上述问题，进一步提高定位的精度。基于DE-PSO算法和牛顿法的协同定位方法步骤如下：

(1) 通过试验装置获取超声波信号，建立基于TDOA信息的代价函数。

(2) 使用DE-PSO算法求解代价函数，得到初步定位结果；根据初步定位结果，计算初始局部放电源距离每个传感器的角度θi和直线距离Ri。

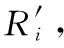
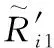
3 验证与分析

3.1 仿真验证

在均匀的传播速度下采用相同的模拟条件，对测量误差方差σ2为10-6、10-5、10-4、10-3、10-2、10-1和100的情况分别进行了500次蒙特卡罗试验。对2个不同位置的局部放电源进行仿真计算，其中p1=[500, 800, 350]T，p2=[620, 400, 550]T，单位均为mm。3种局部放电定位算法的均方根误差如图4所示。由图4可知，DE-PSO算法的均方根误差远小于PSO算法和DE算法的均方根误差，且随着测量误差方差的增大各算法的均方根误差均有增大的趋势。

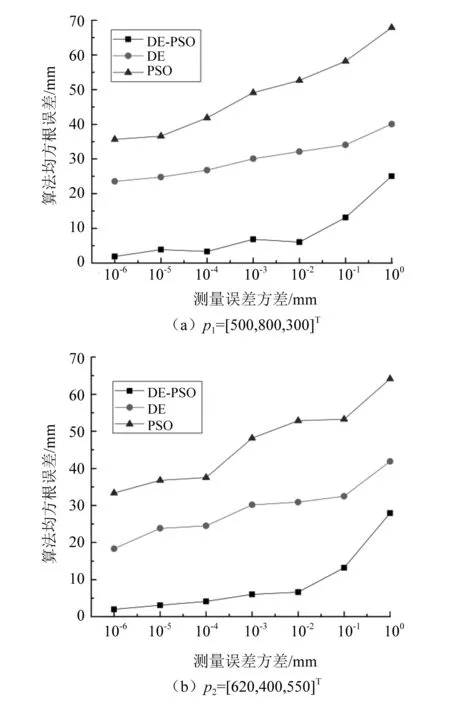
图4 算法均方根误差

3.2 试验与讨论

试验数据取自一台试验变压器，其长、宽、高分别为700 mm、600 mm、1 400 mm，如图5所示。为了生成可预测的局部放电信号，电极系统使用典型的针板结构来模拟局部放电。针尖的曲率半径小于0.1 mm。平面电极的尺寸为50 mm×48 mm×2.5 mm。在针电极和平面电极之间放置尺寸为60 mm×60 mm×1 mm的绝缘纸板，针尖到板的距离控制为4 mm。通过使用四个带宽为100 kHz～400 kHz且共振频率为150 kHz的声发射传感器来测量局部放电。这些传感器通过磁力吸附在变压器的外表面。信号采集设备是一个四通道数字示波器。两种布置方式下四个传感器的坐标如表1所示。

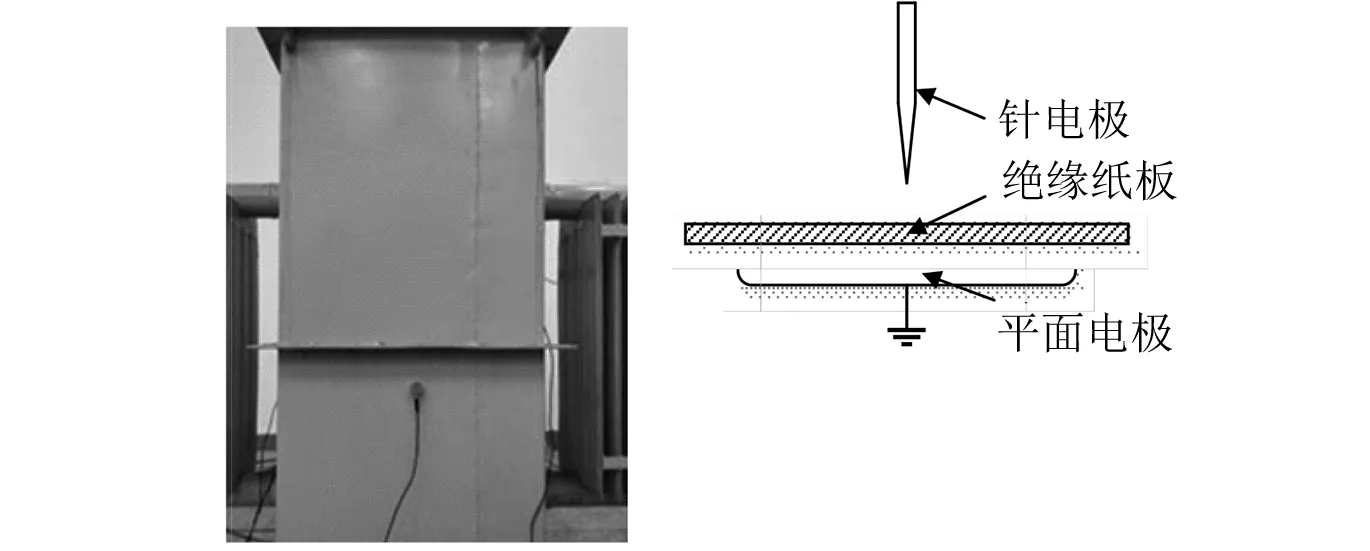
图5 试验变压器

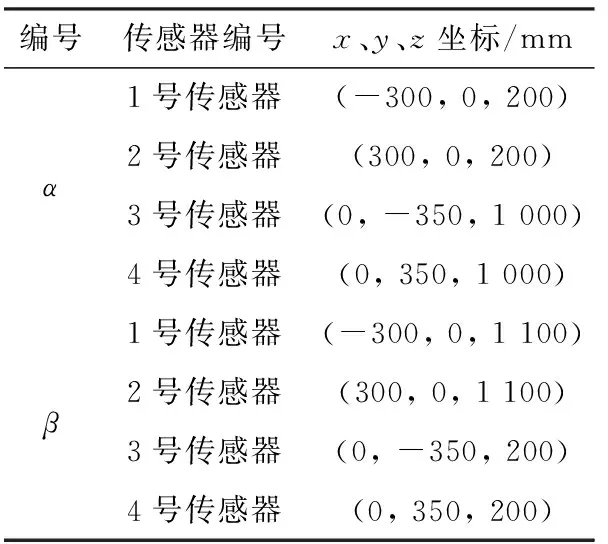
表1 传感器坐标

各种方法计算出的坐标和平均距离误差ΔR如表2所示。可见，PSO算法和DE算法计算出的坐标和实际坐标差距较大，平均距离误差ΔR均在100 mm左右。牛顿法虽然计算出的坐标和实际坐标差距较小，但在传感器α布置方式下存在因初值选取不当而导致结果不收敛的情况，因此可能无法获得局部放电源坐标。混合DE-PSO算法大幅提高了原有的PSO算法和DE算法的准确度，平均距离误差ΔR减少了约一半。而协同算法的定位精度是五种方法中最高的，相比于DE-PSO算法的定位结果，平均距离误差ΔR进一步减少了。

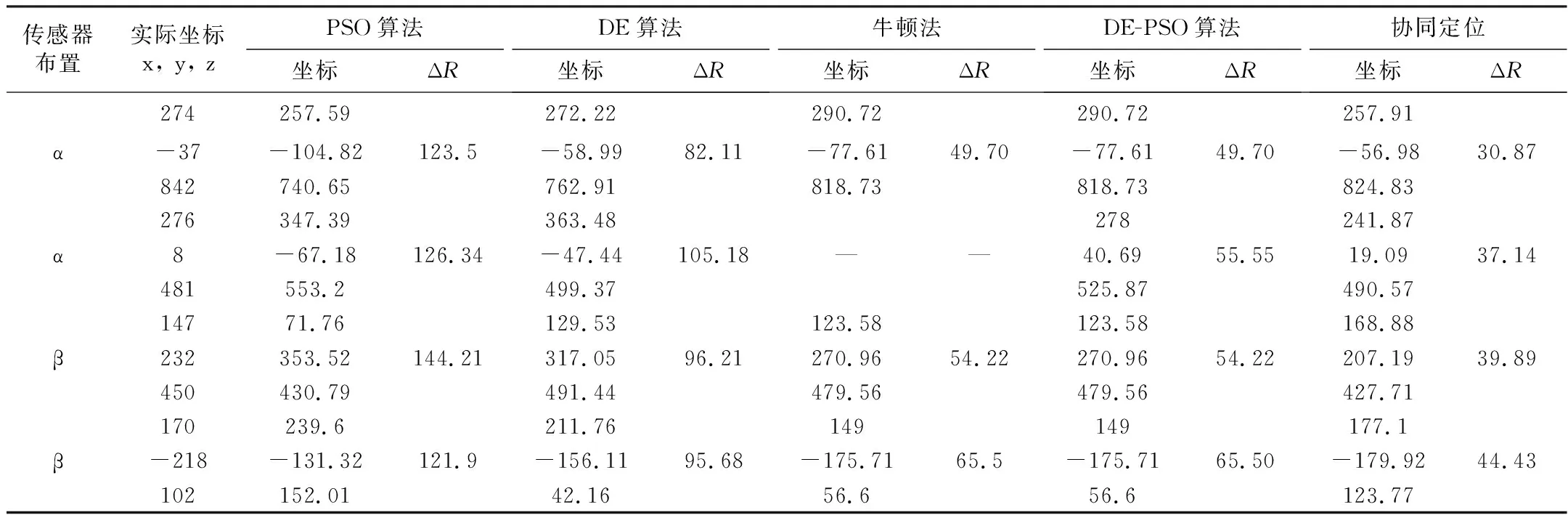
表2 试验结果 mm

4 结束语

本文提出了一种提高车载变压器局部放电定位精度的新方法，并通过仿真和试验分析了基于DE-PSO算法和牛顿法的协同定位方法的性能。将计算结果与现有算法进行比较，结果表明DE-PSO算法对不同的测量噪声具有较高的定位精度和较强的鲁棒性，而协同定位方法进一步提高了局部放电源位置估计的准确性。该方法为车载变压器局部放电定位提供了一种良好的解决方法，具有较高的应用价值。