THE PRECISE NORM OF A CLASS OF FORELLI-RUDIN TYPE OPERATORS ON THE SIEGEL UPPER HALF SPACE∗
Lifang ZHOU(周立芳)Yun FAN(樊云)
Department of Mathematics,Huzhou University,Huzhou 313000,China
E-mail:lfzhou@zjhu.edu.cn;fanyun@zjhu.edu.cn
Jin LU(卢金)
School of Internet,Anhui University,Hefei 230039,China
E-mail:lujin@mail.ustc.edu.cn
Abstract The precise Lpnorm of a class of Forelli-Rudin type operators on the Siegel upper half space is given in this paper.The main result not only implies the upper Lpnorm estimate of the Bergman projection,but also implies the precise Lpnorm of the Berezin transform.
Key words precise Lpnorm;Forelli-Rudin type operators;Siegel upper half space;Bergman projection;Berezin transform
1 Introduction
Forelli-Rudin type operators,including the Bergman projection,the Berezin transform,as well as many other operators generated by the Bergman kernel,are named after the seminal 1974 work of Forelli-Rudin[7]on the Lp-boundedness of the Bergman projection on the unit ball.Two classes of Forelli-Rudin type operators–Ta,b,cand Sa,b,c–associated with the triplet of parameters(a,b,c)de fined in[15],can be seen as generalizations of the Bergman projection and the Berezin transform,where Ta,b,cis related to the Bergman projection,and Sa,b,cis related to the Berezin transform.It is well known that the Bergman projection and the Berezin transform play an important role in function spaces and the theory of operators;see for example[36,37]and the reference therein.
The Lpboundedness,the sharp Lpnorm estimate,and the precise Lpnorm calculation for Forelli-Rudin type operators have been studied very extensively.On the unit ball or on the unit disc,the Lp-boundedness of Ta,b,cand Sa,b,cgenerated by the holomorphic Bergman kernel was studied in[15],and the Lp−Lqboundedness of these operators was studied in[1,30].Obtaining the sharp Lpnorm or the precise Lpnorm for Forelli-Rudin type operators is much more difficult than for their Lp-boundedness.The research on the sharp Lpnorm for the holomorphic Bergman projection dates back to Zhu’s work[35].Later,a quantitative version for Zhu’s result was given by Dostani´c[3],and a conjecture for the precise Lpnorm was also given in[3].Very recently,Liu[16]gave a much more precise Lpnorm estimate for the holomorphic Bergman projection,which improves upon Dostani´c’s conjecture;Liu then gave a new conjecture.A precise Lpnorm estimate for the weighted holomorphic Bergman projection was given in[19].The precise operator norm for the holomorphic Bergman projection from L∞to a Bloch space equipped by different norms was studied in[8–10,24–27].It remains an open problem to calculate the precise Lpnorm for the holomorphic Bergman projection.However,the precise Lpnorm for the holomorphic Berezin transform was calculated by Dostani´c in[4];the high dimensional result is in[22].The precise Lpnorm for Sa,b,cgenerated by the holomorphic Bergman kernel was calculated in[33].There is also some research on harmonic Forelli-Rudin type operators;see[2,21,31].The relationship for Forelli-Rudin type operators Sa,b,cbetween the holomorphic and harmonic was established by a class of integral operators induced by the hypergeometric function;see[34].
In this paper we mainly consider the precise Lpnorm for a family of Forelli-Rudin type operators on the Siegel upper half space.The Siegel upper half space is the set
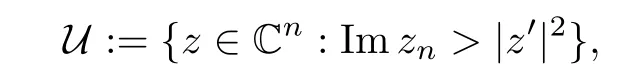
with
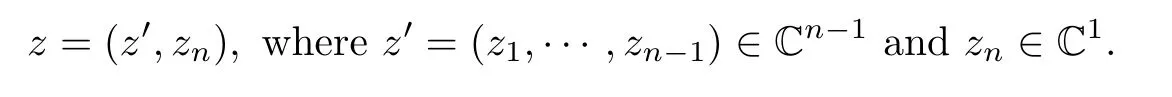
The Siegel upper half space is also called the generalized half-space,since it is the upper half plane when n=1,which follows the terminology of Kor´anyi[11–14].Let dV be the Lebesgue measure on Cn.For α>−1,the weighted Lebesgue measure is de fined by
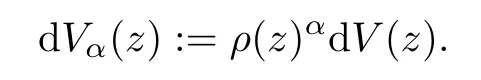
For p>0,the space Lp(U,dVα)consists of all Lebesgue measurable functions f on U for which
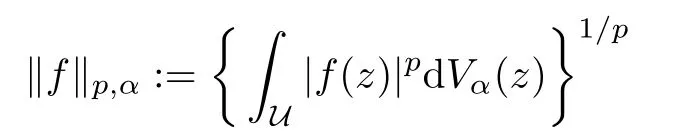
is finite.The Bergman space Ap(U,dVα)is the closed subspace of Lp(U,dVα)consisting of holomorphic functions on U.
Two classes of corresponding Forelli-Rudin type operators–Ta,b,cand Sa,b,c–associated with real parameters(a,b,c)on the Siegel upper half space were studied in[18].Denote
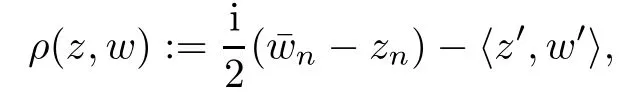
and
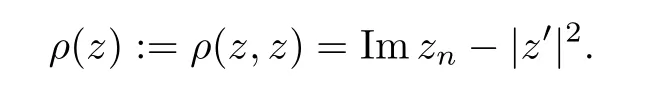
The two classes of Forelli-Rudin type operators generated by the holomorphic Bergman kernel on the Siegel upper half space are de fined by
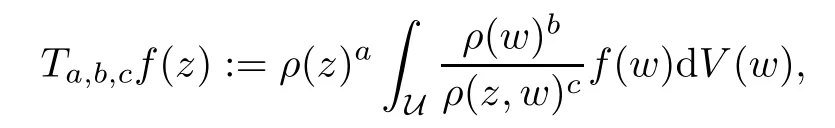
and
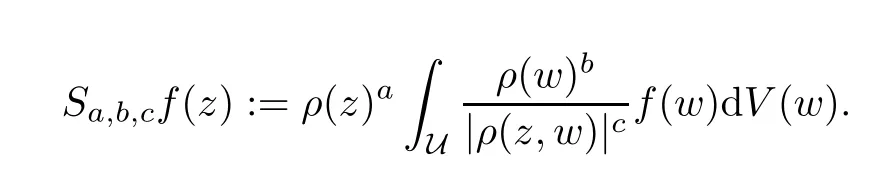
The sufficient and necessary conditions for the Lpboundedness of these two classes of integral operators Sa,b,cand Ta,b,con Lp(U,dVα)were given in[18]by characterizing parameters(a,b,c).The result reads as follows:
Theorem A([18,Theorem 1]) Suppose 1≤p≤∞.Then the following conditions are equivalent:
(1)The operator Ta,b,cis bounded on Lp(U,dVα).
(2)The operator Sa,b,cis bounded on Lp(U,dVα).
(3)The parameters satisfy the conditions
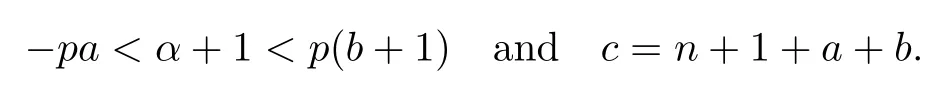
When p=∞,these conditions should be interpreted as
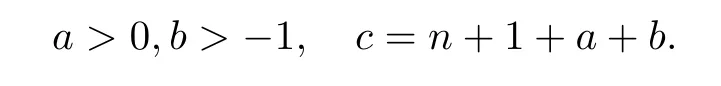
The Lp-Lqboundedness for Forelli-Rudin type operators on the Siegel upper half space or on the upper half plane was studied in[1,20,28].The results on the boundedness of those operators are different from the results on the unit ball because of the unboundedness of the Siegel upper half space and the homogeneity of the Forelli-Rudin type operators.
The problem on the sharp Lpnorm estimates or the precise Lpnorm for Forelli-Rudin type operators on the Siegel upper half space or on the upper half plane have also been studied.Liu[17]gave a precise Lpnorm estimate for the Bergman projection,and also gave a conjecture for the precise Lpnorm.The weighted version was given in[32,Theorem1.1].The precise Lpnorm for the Bergman type projection on the upper half plane,which is Sa,b,cwith(a,b,c)=(0,α,2+α)when n=1,was calculated in[5,23],and the precise Lpnorm for the Berezin type transform on the Siegel upper half space,which is Sa,b,cwith(a,b,c)=(0,α,n+1+α),was calculated in[17,Theorem2].
It is well known that the upper Lpnorm estimates for the Bergman projection and the Berezin transform always come from the precise Lpnorm estimates for Forelli-Rudin type operators Sa,b,cwith some speci fic value of the triplet of parameters(a,b,c).The main purpose of this paper is to calculate the precise Lpnorm of Forelli-Rudin type operators Sa,b,con the weighted Lp(U,dVα)for generalized real parameters(a,b,c).The result is also an extension of the results in[5,17,23].
Our main result is the following:
Theorem 1.1Suppose that α>−1,1≤p≤∞such that−pa<α+1 For any two points z=(z1,···,zn)and w=(w1,···wn)in Cn,we write It is straightforward to calculate that We refer to[29,Chapter XII]and[12,Chapter 9]for the properties of these two mappings.For convenience and for later reference,we record the following lemma: Lemma 2.1The mappings Φ and Ψ have the following elementary properties: (i)The identity holds for all ξ,η∈Bn. (ii)The real Jacobian of Φ at ξ∈Bnis (iii)The identity holds for all z,w∈U,where i=(0,i). (iv)The identity holds for all z∈U. (v)The real Jacobian of Ψ at z∈U is We use the classical notationto denote the hypergeometric functions The hypergeometric series in(2.5)converges absolutely for all|<1. Two formulas which are used throughout the paper are as follows(more properties of hypergeometric functions can be seen in[6,Chapter II]): Lemma 2.2([18,Lemma 5][17,Lemma 13]) Let s,t∈R.Then we have for all z∈U,where Lemma 2.3Let γ>−1 and θ∈R.If θ>0 and 2θ−(n+1+γ)>0,then ProofThe result follows from[17,Lemma 16]and(2.7). Lemma 2.4Suppose that t>−1 and 2s−t>n+1.For 0<δ<1,denote ProofMaking the change of variables w=Φ(ξ)and using(2.3),(2.1)and(2.2),we have The upper estimate is given in[18].It is sufficient for us to give the lower estimate bearing in mind that c=n+1+a+b. If p=1,∞,then,by[34,Lemma 2.6]and formula(2.8),we obtain that If 1 Case 1(n+1+b−a)p>n+2(1+α).For 0 where β:=(n+1+b−a)/2.Note that the assumption(n+1+b−a)p>n+2(1+α)implies that 2βp−(n+1+α)−tp(1+α)>0,which guarantees that ψt∈Lp(U,dVα)for all t∈(0,1/p).Indeed,by applying(2.8),we have This implies that Note that the above hypergeometric function is increasing for λ∈[0,1),since its Taylor coeffi-cients are all positive. Now we think of Hα(t,λ)as a family of continuous functions of t on theindex by λ∈[0,1).These functions tend monotonically to the constant function 1 pointwise as λ↗1,by(2.6).Moreover,the convergence is uniform in t on,by Dini’s theorem. It follows that for any∊>0,there exists a δ>0,sufficiently small and independent of t∈,such that This,together with(3.2),shows that The proof is completed.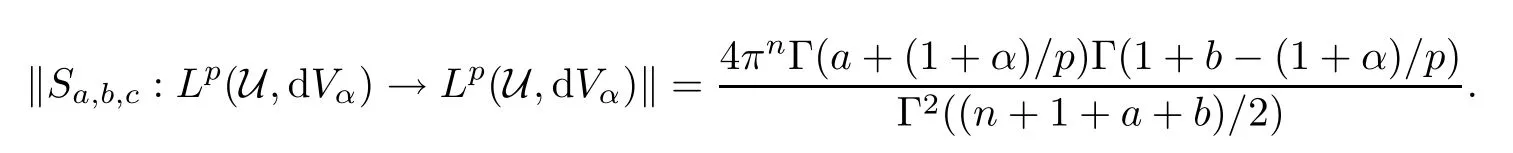
2 Preliminaries
2.1 Cayley transform


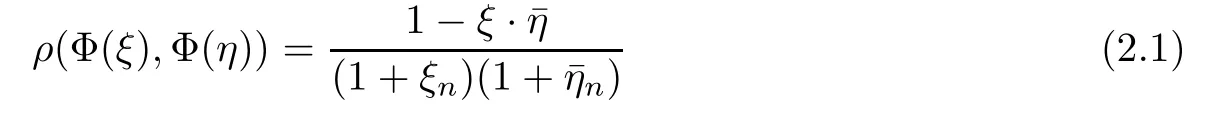

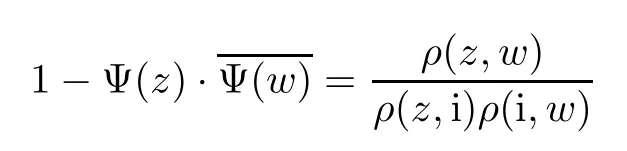

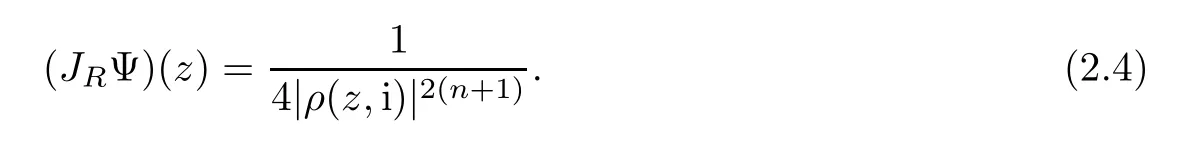
2.2 Hypergeometric functions
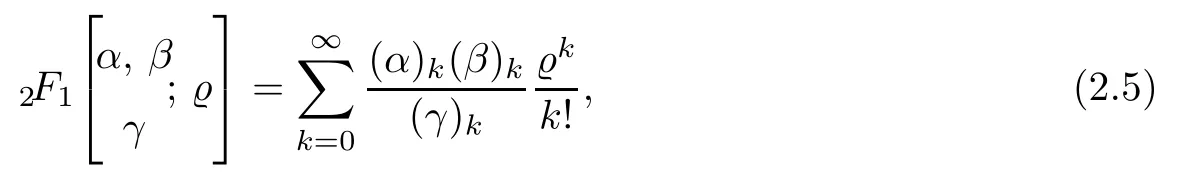
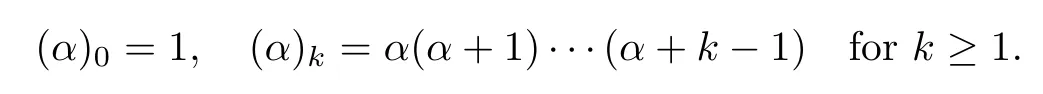

2.3 Integral formulas
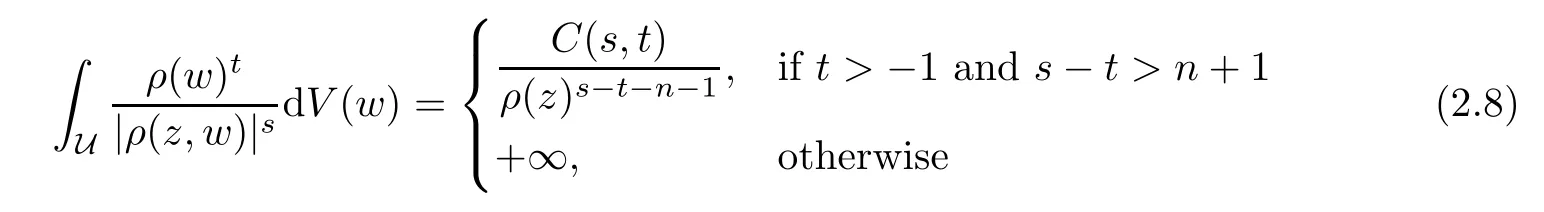
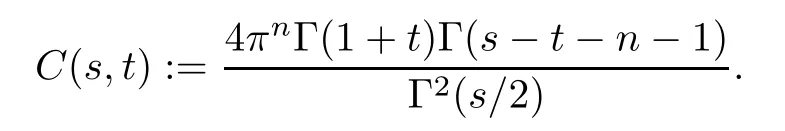
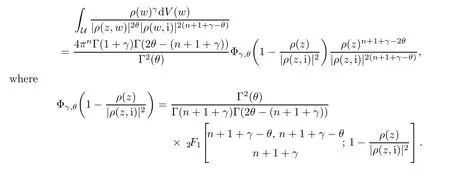


3 Proof of Theorem 1.1
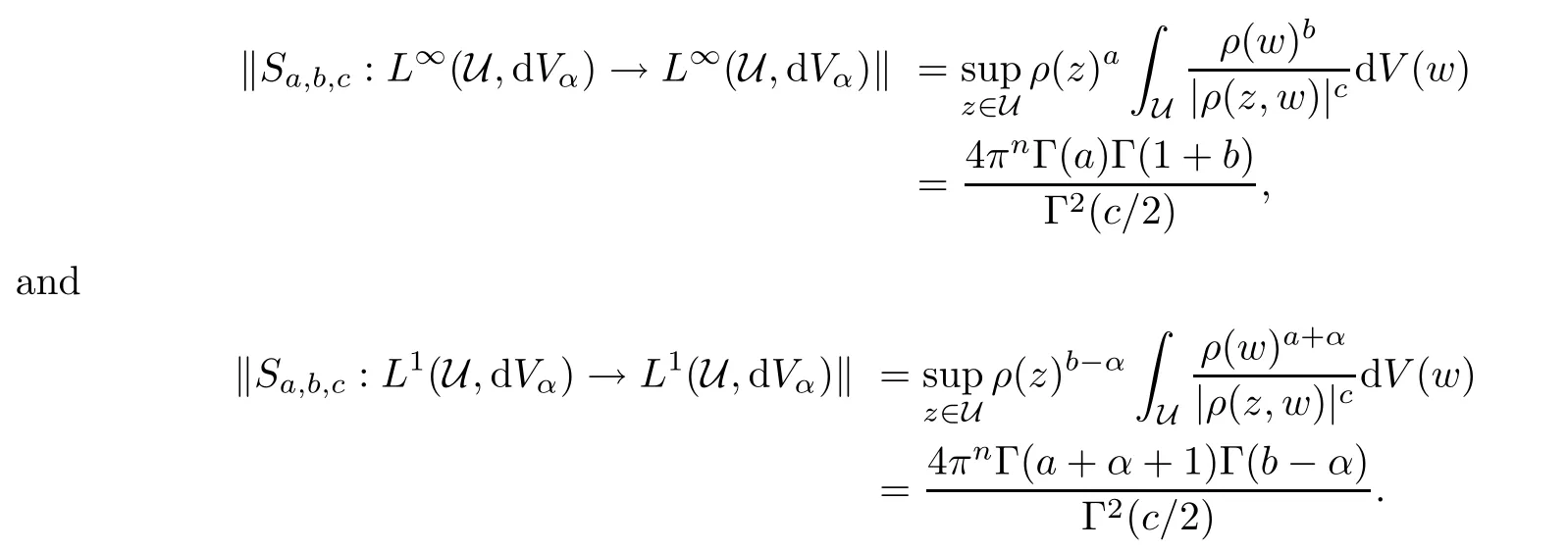
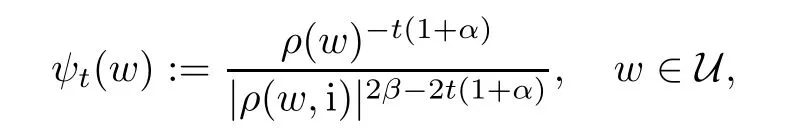
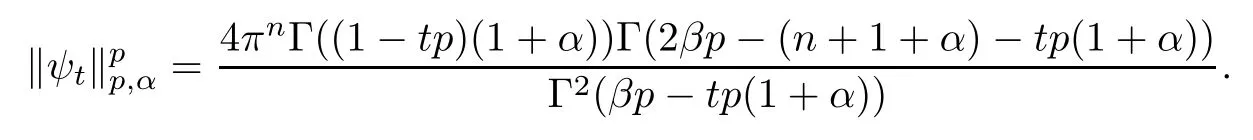
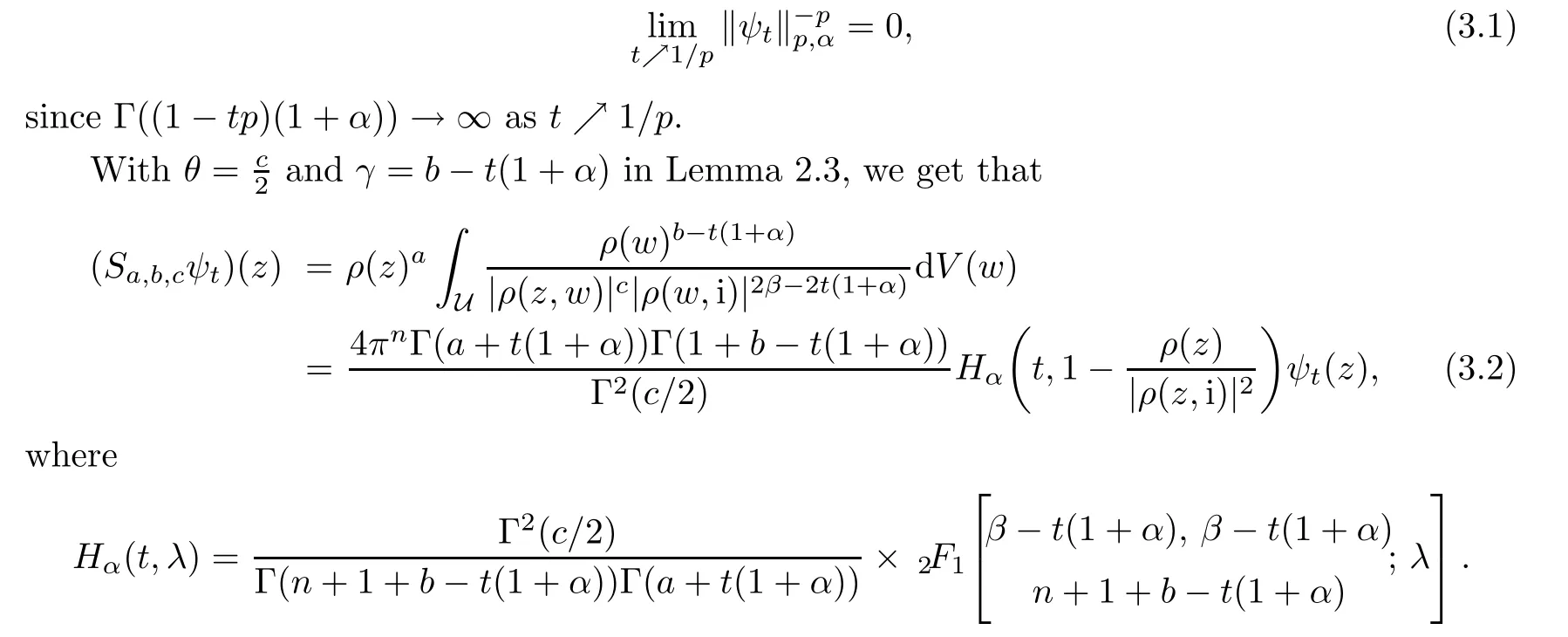




 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
