RIGIDITY RESULTS FOR SELF-SHRINKING SURFACES IN R4∗
Xuyong JIANG(绪永)
Department of Mathematics,Changzhou University,Changzhou 213164,China
E-mail:jiangxy 1@163.com
Hejun SUN((孙和军)† Peibiao ZHAO (赵培标)
College of Science,Nanjing University of Science and Technology,Nanjing 210094,China
E-mail:hejunsun@163.com;pbzhao@njust.edu.cn
Abstract In this paper,we give some rigidity results for complete self-shrinking surfaces properly immersed in R4under some assumptions regarding their Gauss images.More precisely,we prove that this has to be a plane,provided that the images of either Gauss map projection lies in an open hemisphere orWe also give the classi fication of complete self-shrinking surfaces properly immersed in R4provided that the images of Gauss map projection lies in some closed hemispheres.As an application of the above results,we give a new proof for the result of Zhou.Moreover,we establish a Bernstein-type theorem.
Key words self-shrinkers;Gauss map;Bernstein-type theorem;rigidity
1 Introduction
In the theory of minimal surfaces,the elegant theorem of Bernstein plays a fundamental role.It states that a minimal graph in Rde fined on the entire Rmust be a plane.In the view of the value distribution of the Gauss map,the Bernstein theorem can be restated as follows:if the image of a minimal surface in Runder the Gauss map lies on an open hemisphere,then it is a plane.
The Bernstein theorem has been improved and generalized by many mathematicians.Nirenberg conjectured that if the Gauss image of a complete minimal surface in Romits a neighborhood of some point,then it has to be a plane.In 1959,this conjecture was proved by Osserman[1].In 1988,Fujimoto[2]proved that the number of exceptional values of the Gauss map of non-flat complete minimal surfaces in Ris at most four.In 1961,Moser[3]proved that an n-dimensional minimal graph must be a hyperplane,under the assumption of uniformly bounded slope of the graph.In 1969,a counterexample constructed by Bombieri,De Giorgi and Giusti[4]showed that the Bernstein theorem fails in dimension 8 or higher.For graphs of higher codimensions,some Bernstein-type theorems were derived under the assumption of certain quantitative bounded slope of the graphs.The key point of this idea is based on the fact that the composition of a harmonic map with a convex function is a subharmonic function.One can apply the maximum principle on the subharmonic function,taking care with the non-compactness problems,to prove the Bernstein-type theorem.We refer to[5–7]and the references therein for more literature on the Bernstein-type theorems for minimal surfaces.
It is natural to ask whether some analogous results also hold for more general surfaces,like constant mean curvature surfaces.In 1910,Bernstein[8]proved that there is no complete graph of non-zero constant mean curvature in R.In 1965,Chern[9]investigated constant mean curvature graphs in high dimensional Euclidean spaces.Moreover,he also proposed a question on value distribution of the Gauss map of constant mean curvature hypersurfaces.In 1982,Hoffman,Osserman and Schoen[10]proved that if the Gauss image of a complete constant mean curvature surface in Rlies in some closed hemisphere,then it is a plane or a right circular cylinder.For surfaces in R,it is well-known that the Gauss map g of surfaces splits into a pair of maps gand g.In[10],the authors also considered a complete surface in Rwhose mean curvature vector is parallel and non-zero.They proved that if either projection of its image under the Gauss map lies in a closed hemisphere,then it is a right circular cylinder in some R⊂Ror a product of circles.
The field of geometric flows has seen tremendous progress in recent decades.Mean curvature flow is the most natural geometric flow in extrinsic geometry,and has been extensively studied.One of the basic problems in mean curvature flow is to understand its singularity.A self-shrinker is an immersion X:M→Rwhose mean curvature vector satis fies the equation

where Xdenotes the orthogonal projection into the normal bundle of M.Because selfshrinkers describe all possible blow-ups at a given type I singularity of the mean curvature flow,they play an important role in the study of the mean curvature flow.
Self-shrinkers and minimal submanifolds are geometric objects with many similar geometric properties(see[11,12]).It is an interesting question as to whether or not some analogous results hold for self-shrinkers and for minimal submanifolds.In 2011,Wang[13]established a Bernstein-type theorem for self-shrinkers.It states that smooth self-shrinkers in R,that are entire graphs,are hyperplanes.In 2016,Ding,Xin and Yang[14]gave some rigidity results for complete self-shrinking hypersurfaces properly immersed in R,provided the Gauss images are contained in some open or closed hemispheres.Here properly immersed means that the immersion is a proper map.Ding,Xin and Yang also established a Bernstein-type theorem for self-shrinkers with higher codimension,provided that the slope of graphs is bounded by 3.In 2018,Zhou[15]proved that a self-shrinking graphical surface in Rwith the Jacobian satisfying J>−1 or J<1 is a 2-dimensional plane through 0.
In this paper,inspired by the work of[6,10,14,15]etc.,we give some rigidity results for self-shrinking surfaces properly immersed in R.We first derive the following theorem:
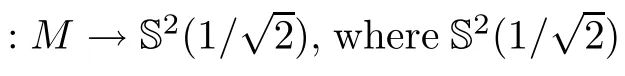

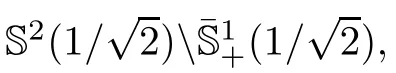
Moreover,we give a classi fication of complete self-shrinking surfaces properly immersed in R,provided that projections of their Gauss map both lies in some closed hemispheres.
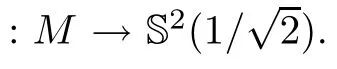
Remark 1.2
Here Abresch-Langer curves contain lines,circles and a family of transcendental curves γgiven by Abresch and Langer in[16].Our results show that the Clifford torus is the unique compact embedded self-shrinking surface if images of both gand glie in some closed hemispheres.Remark 1.3
It is an interesting problem to give the classi fication of self-shrinking surfaces in Rprovided that the image of either gor glies in a closed hemisphere.Theorem 5 in[17]shows that this is equivalent to giving the classi fication of Lagrangian self-shrinking surface.It is natural to conjecture that the Clifford torus is the unique compact embedded self-shrinking surface if the images of either gor glie in some closed hemispheres,which is equivalent to saying that the Clifford torus is the only compact embedded Lagrangian self-shrinker in R.Li and Wang[18],Li and Li[19]gave some new characterizations of the Clifford torus as Lagrangian self-shrinker.Recently,Zhou[15]gave the following Bernstein-type result for graphical self-shrinkers in R4:

1)J(x,y)>−1 for all(x,y)∈R;
2)J(x,y)<1 for all(x,y)∈R.
If its graph is a self-shrinking surface in R,then M is a plane through 0.
As an application of Theorem 1.1,we give a different proof of Zhou’s result.Furthermore,according to our proof,we can generalize this result.In fact,we can find that the following Bernstein-type result is true:
Theorem 1.5
Let f=(f(x,y),f(x,y))be a smooth map from Rinto R.Suppose that the graph M=(x,y,f(x,y),f(x,y))is a self-shrinking surface in R.If there exists a constant unit vector α=(α,α,α)∈Rsatisfying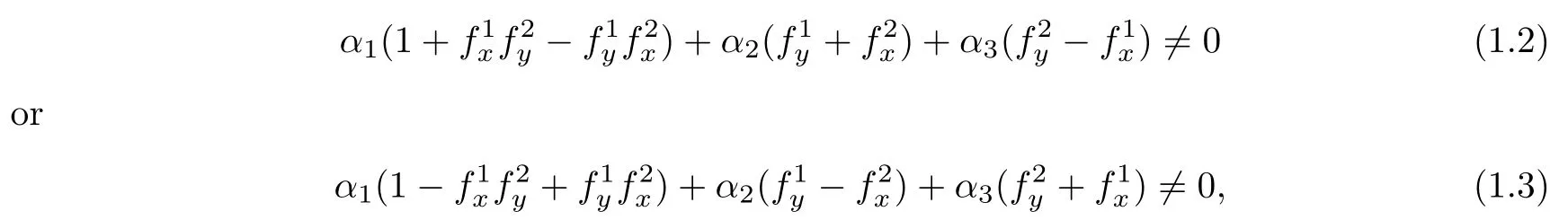
then M has to be a plane through 0.
2 Preliminaries
In this section,for the convenience of the reader,we brie fly recall some basic facts about the geometric theory of surfaces in R,the Grassmannian manifold,Pl¨ucker coordinates,Gauss map and ρ-harmonic map.
Let M be a connected oriented surface and X:M→Rbe an isometric Cimmersion.Let{e,e}be a local tangent orthonormal frame field on M and{e,e}be a local normal orthonormal frame field on M.We de fine the 1-forms
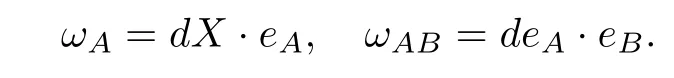
for A,B=1,···,4.Since e·e=δ,we have ω=−ω.Using the Poincar´e formula d=0,the Maurer-Cartan structure equations are given by

In fact,1-form ωis the connection form for the tangent bundle of M,and ωis the connection form for the normal bundle of M.The Gauss curvature K and the normal curvature Kcan also be given by
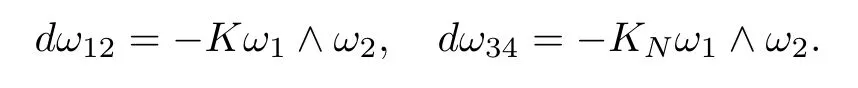
For more references on the geometric theory of surfaces in R,we refer to[20]and the references therein.
The Grassmannian manifold Gis constituted by all oriented 2-planes in R.Let X:M→Rbe an oriented surface in R.We de fine the generalized Gauss map g:M→G,which is obtained by parallel translation of tangent space T(M)of M at the point q to the origin of R.
Gcan be regarded as an embedded submanifold in the 5-dimensional unit sphere S(1)⊂Rby using Plu¨cker coordinates.More precisely,let E,E,E,Ebe an orthonormal frame field in R.A 2-plane Π∈Gis spanned by the orthonormal vectors e,e,where

The Pl¨ucker coordinates p(1≤i Since e,eare the orthonormal frame field of the 2-plane Π,we know that Pl¨ucker coordinates are skew-symmetric in all pairs of indices and satisfy the Pl¨ucker relations Thus,one can establish a correspondence between the 2-plane in Rand the collection of Pl¨ucker coordinates.This gives an embedding G→S(1).Hence,the metric of Gis induced by the embedding in S(1). We refer the reader to[21]for more properties of Grassmannian manifolds and Pl¨ucker coordinates. Assume that(M,g)and(N,h)are two complete Riemannian manifolds.Let ρ:M→R be a smooth function.A map φ:M→N is said to be a ρ-harmonic map if it is a critical point of the ρ-energy functional de fined by The Euler-Lagrange equation for the ρ-energy functional is the ρ-harmonic map equation where τ(φ)=div(dφ)is the tension field of φ and τ(φ)is the ρ-tension field of φ.Let φ:M→N and ϕ:N→P be two maps between complete Riemannian manifolds.Obviously,we have the following composition formula: In particular,if φ is ρ-harmonic and ϕ is totally geodesic,then ϕ◦φ is ρ-harmonic.The concept of ρ-harmonic map between Riemannian manifolds was first introduced by Lichnerowicz[22],and was studied recently by many authors(cf.[23,24]). A metric measure space(M,g,edv)is a Riemannian manifold(M,g)endowed with the weighted measure edv.The weighted Laplacian∆on(M,g,edv)is a second order differential operator de fined by where∆is Laplace operator of the Riemannian manifold(M,g).A metric measure space is called ρ-parabolic if every upper bounded solution of∆f≥0 must be identically constant.We note that for a map φ:M→R,it holds that τ(φ)=∆φ. In this section,we give the proofs of Theorems 1.1–1.5.In order to prove Theorem 1.1,we need Lemmas 3.1–3.3.The following lemma gives a characterization of ρ-harmonic map from Riemannian manifolds to spheres: Combining(3.2)with(3.3),we obtain We can immediately get(3.1)from(3.2)and(3.4).This completes the proof of Lemma 3.1. The following Ruh-Vilms type theorem for self-shrinkers is a key lemma in the proof of Theorem 1.1: Lemma 3.2 1)|F|=|F|; 2)H=0 if and only of F=F=0; 3)K=J+J; 4)K=J−J,where H is the mean curvature vector of M,Jis the Jacobian of the map g,and Now we give the proof of Theorem 1.1. Proof of Theorem 1.1 Now we give the proof of Theorem 1.2. Since M is a self-shrinking surface properly immersed in R,we can find that θ◦gis constant by letting r→∞in(3.11).Hence the image of gis contained in an open meridian.Thus it is contained in an open hemisphere.Then we can get the conclusion from Theorem 1.1.This concludes the proof of Theorem 1.2. In order to prove Theorem 1.3,we need Lemmas 3.4–3.7. Lemma 3.6 Lemma 3.7 Now we give the proof of Theorem 1.3. Proof of Theorem 1.3 It is not difficult to find that if their Jacobian satis fies one of the above conditions,the image of neither gnor glies in an open hemisphere.According to Theorem 1.1,we know that M has to be a plane.This completes the proof of Theorem 1.4. Now we give the proof of Theorem 1.5. Proof of Theorem 1.5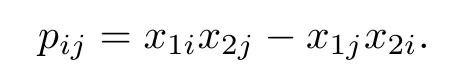

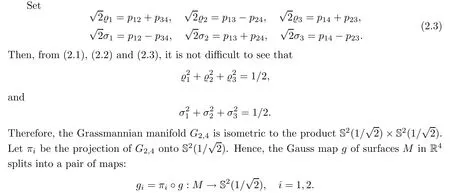




3 Proofs of the Main Results




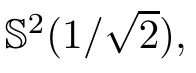
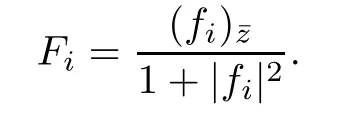
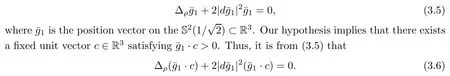
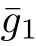
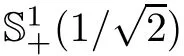
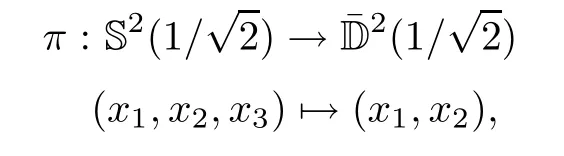






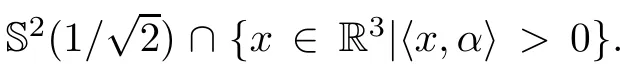
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- GLOBAL STRONG SOLUTION AND EXPONENTIAL DECAY OF 3D NONHOMOGENEOUS ASYMMETRIC FLUID EQUATIONS WITH VACUUM∗
- CONTINUOUS TIME MIXED STATE BRANCHING PROCESSES AND STOCHASTIC EQUATIONS∗
- SOME OSCILLATION CRITERIA FOR A CLASS OF HIGHER ORDER NONLINEAR DYNAMIC EQUATIONS WITH A DELAY ARGUMENT ON TIME SCALES∗
- COARSE ISOMETRIES BETWEEN FINITE DIMENSIONAL BANACH SPACES∗
- ZERO KINEMATIC VISCOSITY-MAGNETIC DIFFUSION LIMIT OF THE INCOMPRESSIBLE VISCOUS MAGNETOHYDRODYNAMIC EQUATIONS WITH NAVIER BOUNDARY CONDITIONS∗
- THE PRECISE NORM OF A CLASS OF FORELLI-RUDIN TYPE OPERATORS ON THE SIEGEL UPPER HALF SPACE∗
