分布式驱动电动车自抗扰控制电子差速研究

任周强

（长安大学 汽车学院，陕西 西安 710064）

引言

传统汽车在转弯行驶过程中时，采用机械差速器实现内外侧车轮之间的差速转向，而分布式驱动电动汽车采用的是轮毂电机直接驱动车轮，因此采用电子差速代替传统的机械差速器，所谓电子差速是通过电控方式控制转向时各个车轮的速度，来保证车辆在转向过程中各轮以纯滚动方式运动。目前，电子差速的控制方式主要有两种，一种是基于转矩的电子差速控制，另一种是基于转速的电子差速控制。本文设计了一种基于自抗扰控制器的差速控制策略[1]，通过阿克曼转向模型[2]获取转向工况中各车轮的理想转速，采用自抗扰控制器对车轮的实际转速进行控制以追踪理想值。自抗扰控制[3]作为一种新型控制技术，能对系统运行过程中收到的复杂扰动实时估算并补偿，适用于非线性系统，应用于电子差速控制中具有较好的效果。

1 车辆转向运动学模型

假设汽车是一个刚体，则汽车转弯时满足阿克曼模型。依据阿克曼转向模型，如图1所示，4个车轮的瞬时转向为O。其中，δ为车辆转向角，δ1为左前轮转向角，δ2为右前轮转向角，l1为质心到前轴的距离，l2为质心到后轴的距离，d为轮距，R0为车辆转向半径；Ri(i=1,2,3,4)为驱动轮绕瞬时转向中心O的转向半径。

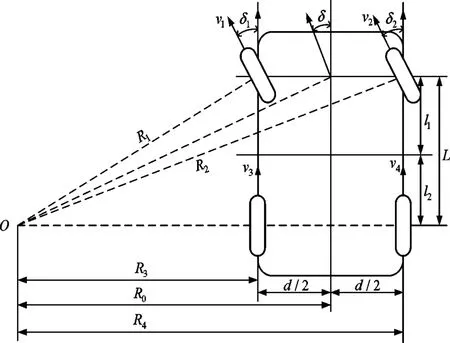
图1 阿克曼转向模型

车辆转向角δ作近似计算：

由阿克曼模型图可以得到当前车辆转向角δ与各车轮理想转向半径Ri(i=1,2,3,4)之间的关系：

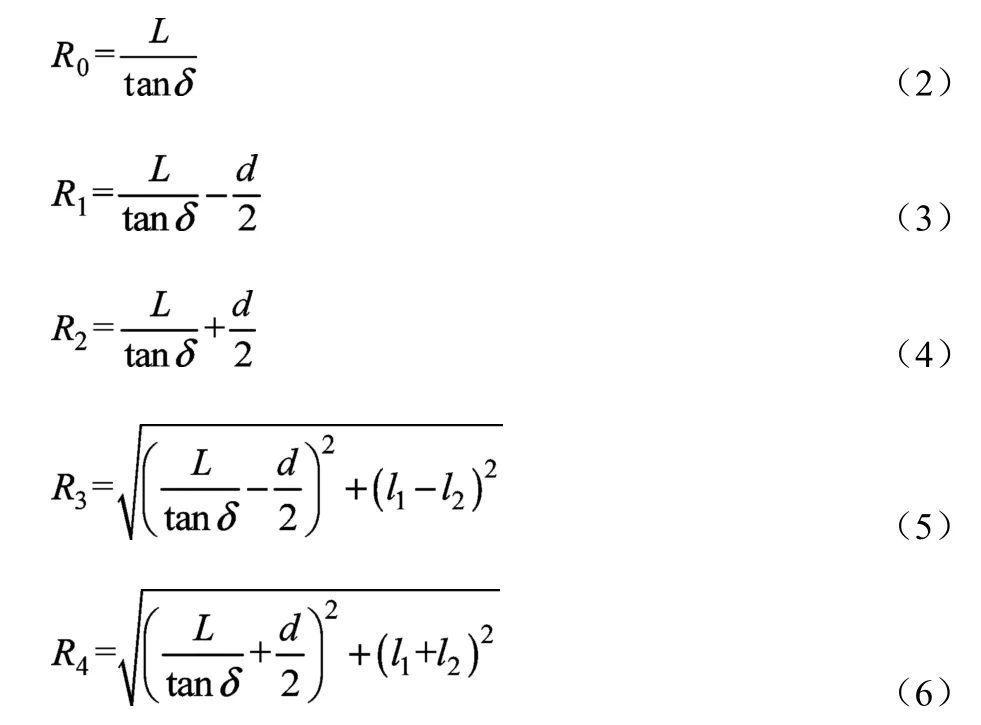
若车轮滚动半径为r，各个车轮在转向过程中绕瞬时转向中心O的期望转速，即电机转速为：

2 基于轮速的自抗扰控制器设计

2.1 轮速跟踪微分器

轮速跟踪微分器（TD）的作用是完成对输入信号的跟踪，提取含有随机噪声的输入信号及其微分信号，在保证快速性的同时减少跟踪信号的超调和振荡，理想轮速ωref的跟踪微分方程为：

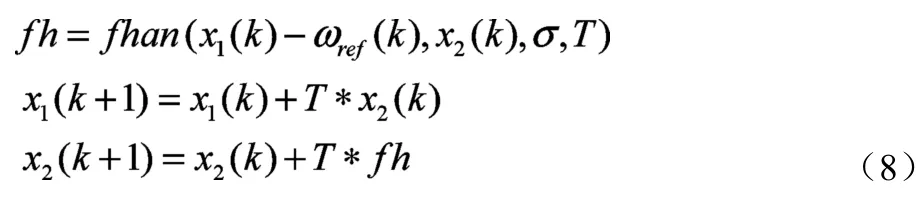
式中，T为采样周期；ωref(k)为第k时刻的输入信号；σ为决定跟踪快慢的参数；fhan(．)函数为最速控制综合函数，描述如下：

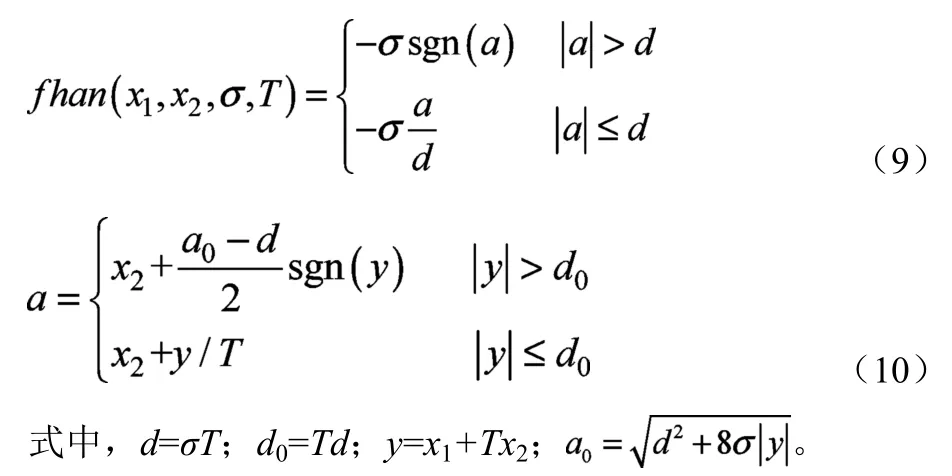
输入信号为ωref(k)，采用式（1）可实现x1(k)→ωref(k)，x2(k)→ωref(k)，如果ωref(k)是带有噪声的信号，微分器可同时实现滤波。

2.2 轮速扩张观测器设计

扩张观测器（Extended State Observer, ESO）的特点是估计系统内外扰动的实时作用值，并在反馈中给予补偿，用补偿的方法消除扰动的影响，从而具有抗干扰的作用。实际轮速ωi的扩张观测方程为：

式中，y(k)为输入信号，也就是车辆运动过程中的实际轮速；v1(k)为对输出的估计；v2(k)为对象输出的估计值的一阶导数；v3(k)为对系统总扰动的估计；l1、l2、l3为非线性最优综合控制函数fal的系数，其值决定了ESO对状态变量的估计效果；β为fal函数的滤波因子；fal(．) 函数为非线性函数，描述如下：

式中，δ为fal(e,α,β)函数线性段的区间长度；sgn(．) 为符号函数；α为可调参数代表了函数增益。

2.3 轮速非线性状态误差反馈控制器设计

传统的PID控制形式为误差的现在（P）、过去（I）以及将来（D）的线性组合，这种组合显然具有局限性，可以在非线性范围内寻找更有效的组合形式，本文设计了一种PD形式的非线性组合，控制方程可表示为：

式中，0＜α1＜1＜α2；kp=ε1；kd=ε2；e1为理想轮速与实际轮速估计值之差；e2为理想轮速信号微分与实际轮速微分输出之差。

2.4 基于轮速的电子差速自抗扰控制结构

基于上面所设计的微分跟踪器、扩张状态光测器和非线性状态误差控制器，我们以通过阿克曼转向模型所计算出的车辆转向过程中的理想车轮转速ωref和通过轮速传感器所获得的实际轮速y作为输入，搭建二阶非线性自抗扰控制器，其结构如图2所示。

图2 自抗扰控制器结构

3 基于轮速的电子差速控制策略

为了实现分布式驱动电动汽车的差速转向，本文设计了基于车轮转速的电子差速控制策略，如图3所示。在车辆转向过程中，基于当前车速v与前轮转角δ通过阿克曼理想转向模型计算出车辆转弯时4个车轮所需的理想转速，将计算所得的理想轮速与轮速传感器所采集的实际轮速作为自抗扰控制器的输入，调节后的输出作为轮边驱动电机的输入来调节驱动转矩，最后输入到整车模型，从而通过自抗扰控制器完成对每个车轮理想转速的速度跟随，实现分布式驱动电动汽车的差速控制。

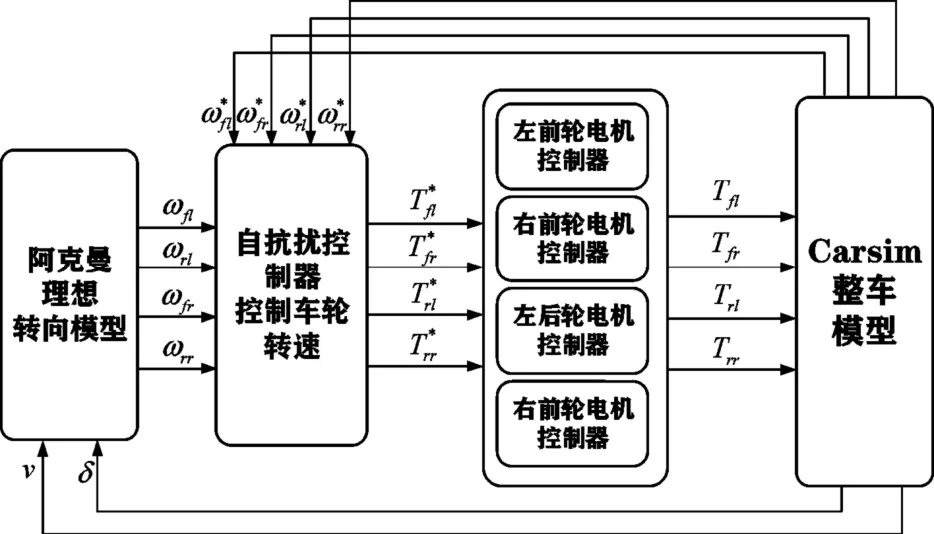
图3 电子差速控制策略

4 仿真试验验证

为了验证差速控制策略的正确性。我们在40 km/h的车速下分别进行方向盘正弦输入和双移线仿真实验。当方向盘转为正弦输入时，仿真实验结果如图4、图5所示；双移线工况下的仿真试验结果如图6、图7所示。

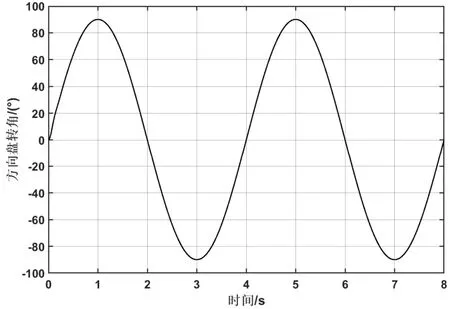
图4 方向盘转角输入曲

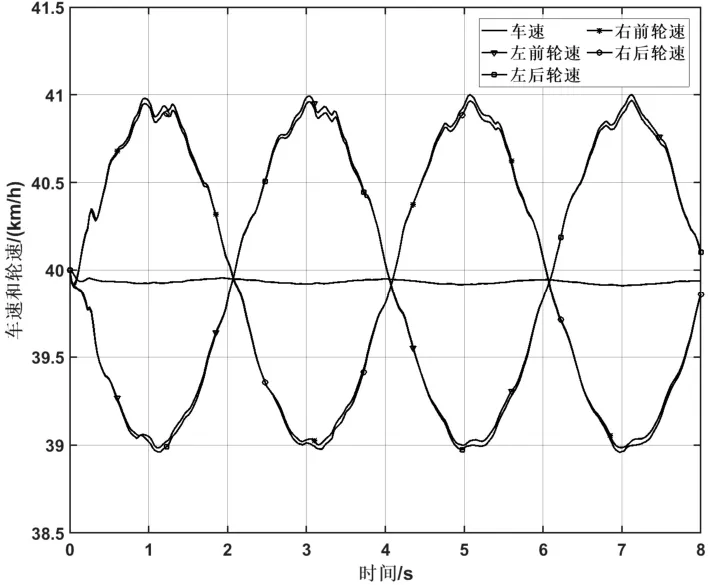
图5 正弦输入下车速及轮速变化曲线

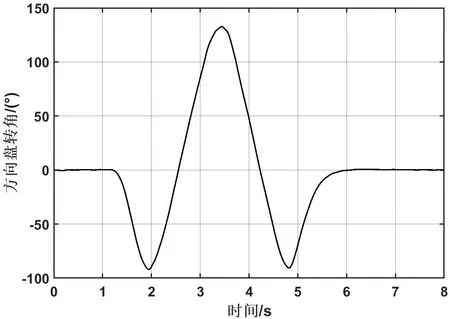
图6 方向盘转角输入曲线

图7 双移线输入下车速及轮速变化曲线

从图5和图7可以看出，车辆在40 km/h的车速，转向盘转角分别为正弦输入和双移线输入的工况下，左右侧车轮均可跟踪到基于Ackermann-Jeantand 模型所计算的各轮理想轮速，实现车辆在转弯行驶下的差速控制。通过两种转向工况下的仿真试验，表明Ackermann-Jeantand 转向模型与自抗扰控制的结合在分布式驱动电动汽车的转向过程中具有良好的差速控制效果。

5 结束语

为了实现分布式驱动纯电动汽车转向时的电子差速控制，本文基于Matlab、Smulink与CarSim建立分布式驱动电动汽车模型，根据Ackermann转向模型设计了基于自抗扰控制的轮速控制器。最后，建立Carsim与Simulink联合仿真，选择方向盘正弦输入和双移线输入来对车辆的差速控制进行 仿真验证，仿真结果表明在转弯时，我们所设计的基于自抗扰控制的轮速控制策略实现了转弯时过程中差速控制功能，证明了控制策略的可行性和合理性。