串行轴承组均载性能及承载能力分析*

卢立河,赵 晶,王世杰

(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)

0 引 言

作为一种采油设备,在现阶段,潜油螺杆泵采油设备需要优化的问题主要包括:井下机组下潜深度、设备工作效率以及可靠性,而增加井下机组下潜深度、提高净扬程的关键难题是提升井下机组部分的轴向承载能力与耐热性能[1]。

球铰型自动调心联轴体[2]承受螺杆泵的轴向载荷。根据目前的井下机组下潜深度统计,系统轴向力的总和为50 kN～120 kN不等[3],由于轴承使用工况苛刻,导致现行的标准轴承使用寿命短,承载能力不高。

王世杰、王雷[4]对潜油螺杆泵采油系统中的推力轴承进行了有限元分析,提出了改变轴承局部品质方案,但是其效果不甚理想。邱靖凇[5]提出了采用轴承串结构的方法,但由于其结构限制,仅能实现梯度分载,对于轴承承载能力的提高效果还十分有限。王世杰[6]提出了一种基于“平衡抵消”原则的双进单出螺杆泵,但受限于国内现有的制造水平,该种螺杆泵尚未能得到实际工程应用及推广。另外,目前还有一种方法是采用氮化硅及氧化锆陶瓷材料制造轴承,但是受限于高昂的制造成本,使得该类轴承也难以批量投入使用。

为克服上述这一瓶颈性问题,笔者从结构设计角度出发,提出了轴承的优化设计方案,并提出了用串联轴承组来代替单一轴承[7-12]的方案。基于“串联结构,并行均载”的设计理念,笔者开展了针对轴承结构的创新研究,其目的是使轴承组中,各级轴承单元能够平均承担螺杆泵转子反馈的轴向载荷,减少各级轴承单元的轴向载荷,以求提高轴承的可靠性,从而打破油井径向尺寸以及下潜深度的限制,进而提高潜油螺杆泵采油系统的整体可靠性。

笔者应用数值仿真方法对轴承组的均载效果和承载能力进行研判,分析创新结构较原有结构的优化效果,提出研究潜油螺杆泵采油系统轴向承载能力的一种可行方法,为极端工况下需提高限径轴承承载能力和可靠性的其他装置提供借鉴。

1 串行轴承组结构及工作原理

串行轴承组(简称轴承组)通常采用串联结构。此处以三级轴承组为例,轴承组的结构图如图1所示。

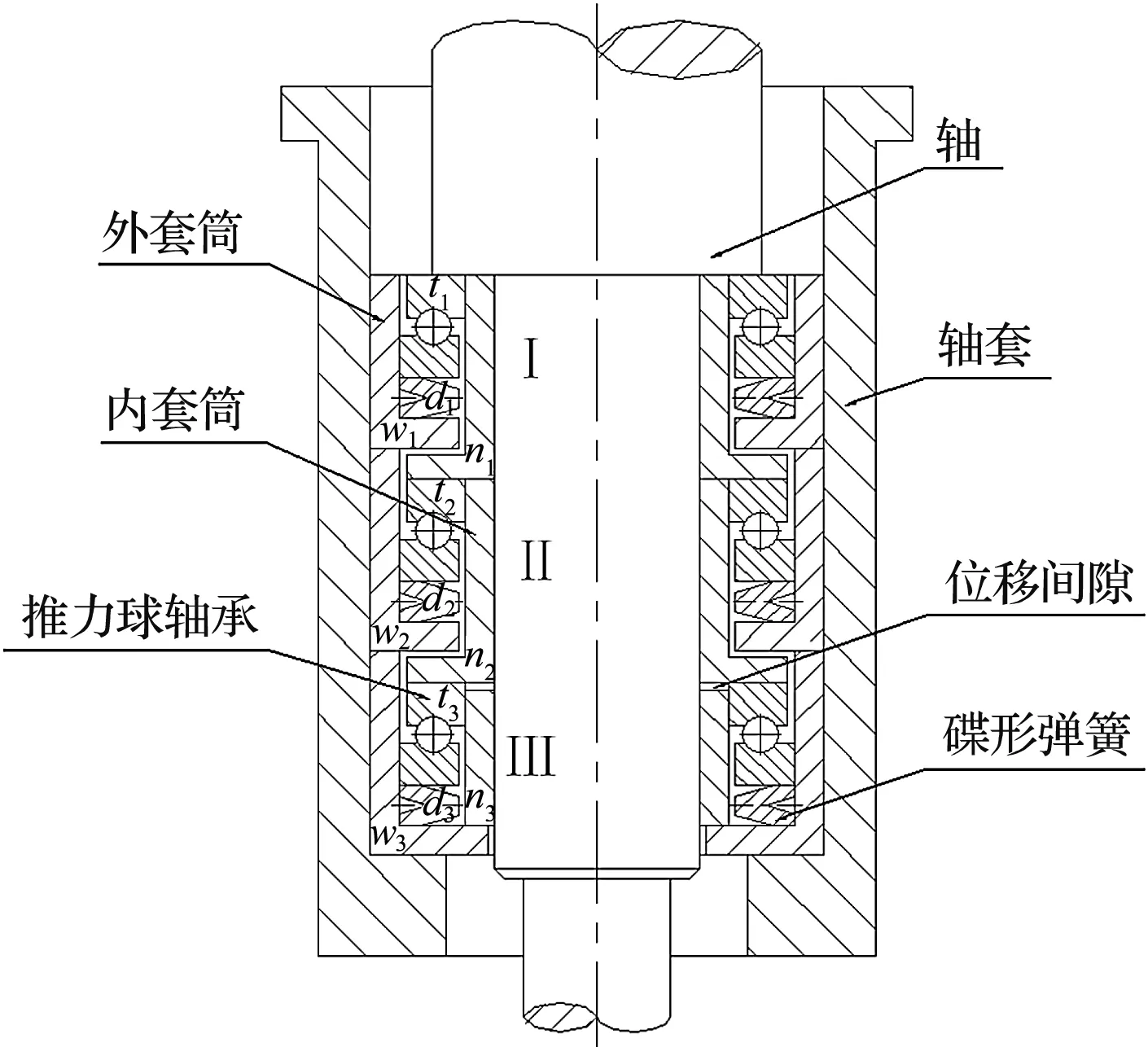
图1 轴承组结构图w1～w3—外套筒;n1～n3—内套筒;t1～t3—推力球轴承;d1～d3—碟形弹簧

由图1可见:轴承组由碟形弹簧、推力球轴承、轴、轴套以及内外套筒组成,各级外套筒之间紧密连接,底座紧压碟形弹簧、推力球轴承,起支撑定位及承载作用;各级内套筒之间仅最后一级与上一级留有轴向位移间隙,即Ⅲ级内套筒n3与Ⅱ级内套筒n2间留有轴向位移间隙,其余内套筒之间均紧密衔接,起到向下一级轴承传递轴向载荷的作用。

当潜油螺杆泵工作时,推力球轴承轴圈、内套筒随轴进行回转运动,座圈及碟形弹簧紧接外套筒固定不动,起固定支撑轴旋转的作用,各级碟形弹簧同时开始承载变形。需要注意的是,各级推力球轴承轴圈均随轴转动。因此,鉴于功能实现的需要,串行轴承组内各级推力球轴承的轴圈均缩进1 mm,碟形弹簧尺寸在选取标准碟形弹簧的基础上也经过非标加工支撑面,均不是标准件。

轴承组的工作原理是:在潜油螺杆泵采油系统开始工作时,螺杆泵转子反馈的轴向力通过轴传递至Ⅰ级推力球轴承t1,同时内套筒n1受力将轴向载荷传递至Ⅱ级推力球轴承t2;以此类推,直至Ⅲ级,此时各级碟形弹簧承载相应的变形;当碟簧变形量累积达到轴向位移间隙时,各级轴承单元即实现了对轴向载荷的均载。

2 轴承组均载理论分析

在系统轴向载荷F(定值)作用下,轴承组中各级碟形弹簧产生轴向弹性变形;各级轴承单元滚动体与滚道面之间产生弹性接触变形;各级内、外套筒均产生微量变形。

此处笔者采用弹性系统对轴承组进行描述,其等效力学模型如图2所示。

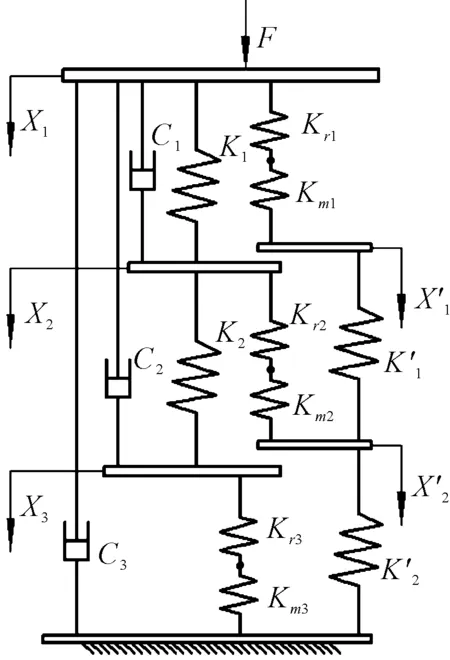
图2 等效力学模型F—系统总的轴向载荷,N;K1,K2—内套筒的轴向刚度,外套筒的轴向刚度,N/m;Kr1～Kr3—(滚动体)接触刚度,N/m;Km1～Km3—碟形弹簧的轴向刚度,N/m;X1～X2—碟形弹簧受载产生的变形量,内套筒传递载荷产生的行程,mm;C1～C3—轴承组各部件相对运动可能产生的摩擦阻尼,N,如碟簧外圆面与外套筒内圆面间相对运动可能产生的摩擦阻尼

此处应用机械阻抗分析法,得到该力学模型的等效机械网络,如图3所示。

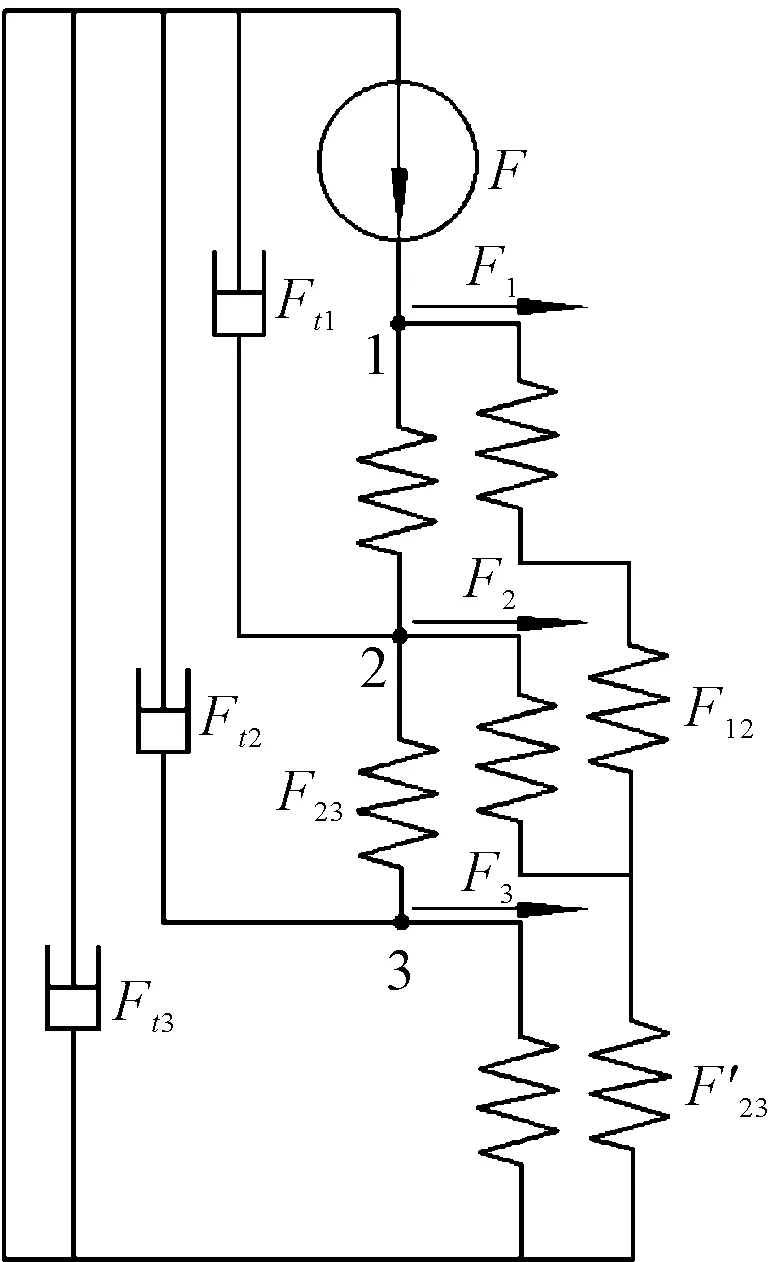
图3 等效机械网络F1～F3—各级轴承单元轴向力,N;F12—分载传递至Ⅱ、Ⅲ级轴承单元时总的轴向力,N;F23～F12—分载传递至Ⅲ级轴承单元的轴向力,传递至Ⅲ级外套筒w3的轴向力,N;Ft1～Ft3—轴承组各元件相对运动可能产生的摩擦阻力,N

在理想条件下,理论上轴承组各元件间均采用间隙配合,故本文不考虑摩擦阻力Ft1～Ft3的影响。因此,根据图3等效机械网络中节点力的平衡关系,可以得出1～3节点的力平衡方程组为:

(1)

要使各级轴承单元实现均载,即各级轴承单元载荷F1～F3相等,且均等于Fa/3,笔者将该值回代式(1),可得:

(2)

同理,将其推广至Z级轴承单元构成的轴承组均载时,应有:

(3)

其中:i=1,2,3……Z-1。

(4)

已知选择的轴承为同型号同规格,即各项参数均相等,根据上述应力公式可得到下式:

σⅠ=σⅡ=σⅢ

(5)

式中:σⅠ,σⅡ,σⅢ—Ⅰ、Ⅱ、Ⅲ级轴承单元滚动体应力值,MPa。

由式(5)可知:理论上Ⅰ、Ⅱ、Ⅲ级轴承单元滚动体应力值相等,可达到各级轴承单元接触内载荷分布均匀性的目的,从而降低轴承组轴承单元最大接触应力值,最终实现提高轴承寿命的目的[13]。

假定各级内、外套筒厚度相等,各级滚动体直径相等,内套筒传递轴向载荷,碟形弹簧分流轴向载荷,显然其轴向刚度必须满足以下配比关系:

Km1=Km2……=KmZ

(6)

K1=K2……=KZ-1

(7)

3 承载能力仿真分析

为验证轴承组结构对轴向载荷的均载效应,降低轴承组轴承单元最大接触应力,需先对原有的单一轴承结构进行必要的仿真分析,以得出等效应力、应变,从而将其与轴承组仿真数据进行对比,进而分析轴承组结构的优化效果。

3.1 单体推力球轴承应力与应变分析

笔者选取的标准推力球轴承型号为51410。此处根据轴圈结构功能的需要,外径缩进1 mm,因此,为区别于标准51410,笔者将该轴承命名为51410a。事实上经过仿真验证对比,51410a与51410的轴向承载能力趋于一致,其参数如表1所示。

表1 51410a推力球轴承几何参数

3.1.1 轴承模型的构建

考虑到推力球轴承是轴对称结构,笔者选取轴承的1/4作为分析对象,在Creo软件建立了51410a推力球轴承的三维几何模型,其中,滚动体数目为8个,直径为21.5 mm,并进行了模型简化,依据圣维南定理[14,15],去除了对整体应力分布无明显影响的结构。

由于推力球轴承的保持架、圆角、游隙等对应力应变的影响几乎可以忽略不计,笔者在建模时忽略圆角、游隙等因素;同时为了建模方便,节约计算资源,忽略了保持架对有限元分析结果的影响[16,17]。

笔者将51410a三维几何模型另存为51410a.stp格式,导入到ANSYS Workbench。材料设置为轴承钢GCr15,由于导入的模型粗糙不便于计算求解,此时需要对模型进行拓扑优化处理;由于软件无法自动识别导入模型为四分之一,需对模型进行轴对称设置,新建Cylindrical坐标系设置轴对称,利用Symmetry功能设置轴对称;单元类型选择为8节点solid45号单元,在此基础上笔者用网格划分功能自动生成网格,共划分了23 913个网格单元,生成了52 361个节点。

3.1.2 载荷与约束施加

笔者模拟轴承的实际工况、装配条件,在轴承座圈底部施加固定约束,对顶部模拟轴施加21 500 N的轴向载荷,轴径为100 mm。

3.1.3 接触对设置

接触对的设置是轴承接触分析的重要环节,根据接触对指定原则[18],笔者设置滚动体表面为接触面,轴圈、座圈滚道面为目标面;设置滚动体与轴圈、座圈滚道面接触类型为Frictional,考虑渗砂、高温、重载及脂润滑条件，设置滚动摩擦系数为0.1。

3.1.4 结果分析

经ANSYS Workbench软件分析计算所得51410a推力球轴承仿真结果如图4所示。

(a)51410a等效应力

从图4中可以看出:(1)51410a等效应力最大值为586.05 MPa,主要集中在滚动体与滚道面接触位置;(2)等效应变最大值为0.003 962 8,主要集中在滚动体与滚道面接触位置。

3.2 轴承组承载能力分析

为与上述单体轴承作对比,本文采用51410a轴承对轴承组进行仿真计算,以得出轴承组的等效应力、应变值,据此分析轴承组结构的优化效果。

轴承组的几何特征参数如表2所示。

表2 轴承组几何特征参数

3.2.1 二级轴承组仿真及结果分析

(1)轴承组模型的构建

轴承组是具有高度非线性行为的多对接触单元的组合体,考虑到整个轴承组是轴对称结构,笔者取整个轴承组模型的1/4进行数值模拟分析;为了建模方便,节约计算资源,进行模型简化,去除对整体应力分布无明显影响的结构,笔者作如下的设定[19]:略去轴套及保持架不计;不计轴承组的自重;略去倒角、圆角、游隙等不计。

将轴承组几何模型导入到ANSYS Workbench仿真软件中的Static Structural模块,以及设置轴对称、拓扑优化等过程,均与上述单体轴承的仿真过程相同,因此此处本文不再赘述。需要指出的是,轴承组碟簧采用一级对合组合型式,为便于仿真分析,笔者将碟簧对设置为一体。

再依次设置轴承组材料:轴承材料为轴承钢GCr15,碟簧材料为弹簧钢60Si2Mn,内外套筒及轴材料均为45钢;单元类型选择为8节点solid45号单元,在此基础上用网格划分功能自动生成网格,共划分39 232个网格单元,生成124 891个节点。

(2)载荷与约束施加

笔者模拟轴承组的实际工况、装配条件,轴承组外套筒底面、外圆面施加固定约束,轴承组顶部模拟施加21 500 N的轴向载荷,轴径为100 mm。

(3)接触对设置

多零件表面发生接触时,笔者根据接触对指定原则,设置滚动体表面为接触面,轴圈、座圈滚道面为目标面,其余设置均遵循指定原则;设置滚动体与轴圈、座圈滚道面接触类型为Frictional,考虑渗砂、高温、重载及脂润滑条件，设置滚动摩擦系数为0.1;外套筒与碟簧及内套筒、外套筒之间、轴承与碟簧、轴与轴承的接触类型均设置为Bonded;碟簧与外套筒,内套筒与轴、轴承的接触类型均设置为No Separation。

(4)结果分析

二级轴承组仿真分析结果如图5所示。

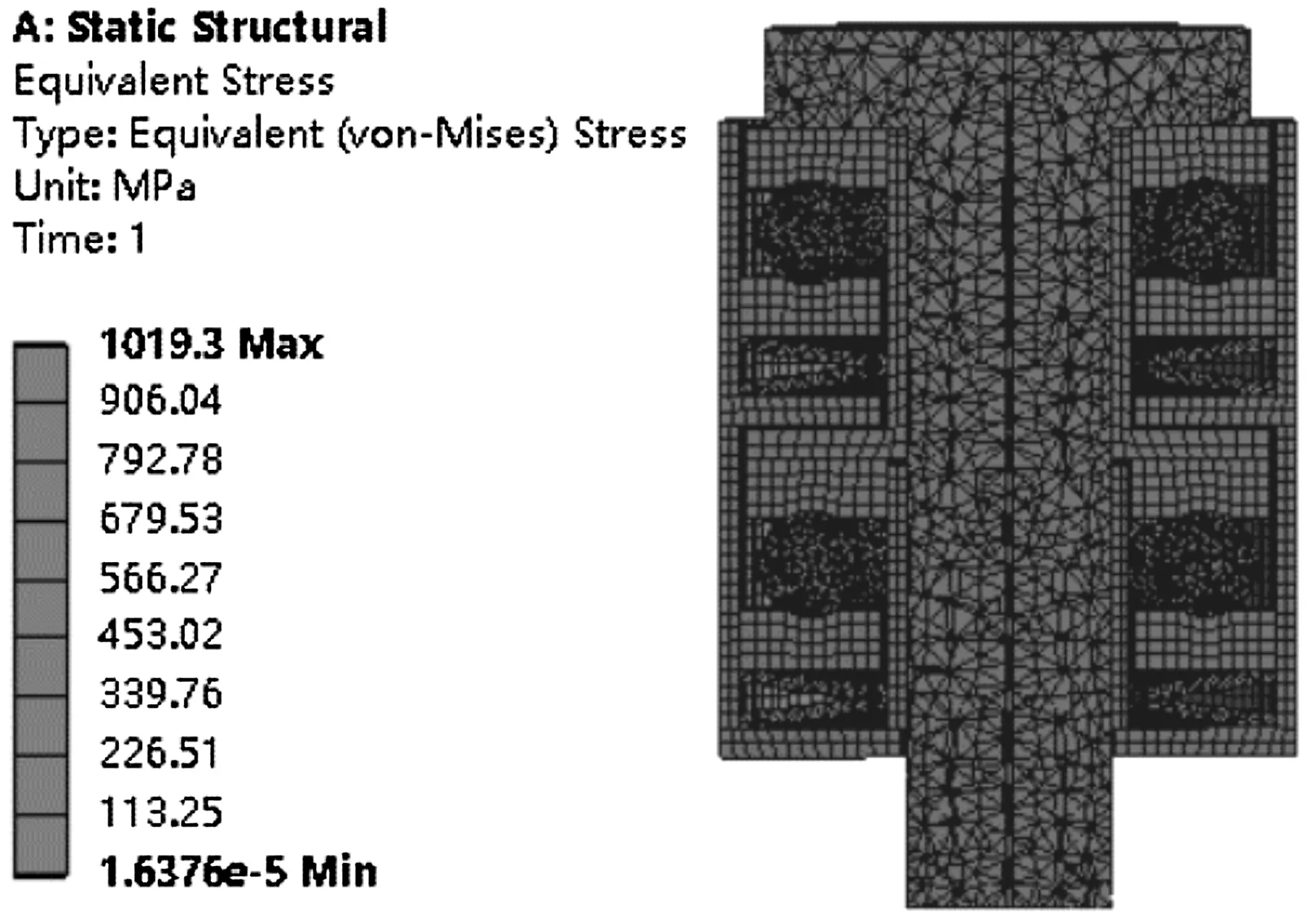
(a)二级轴承组等效应力云图

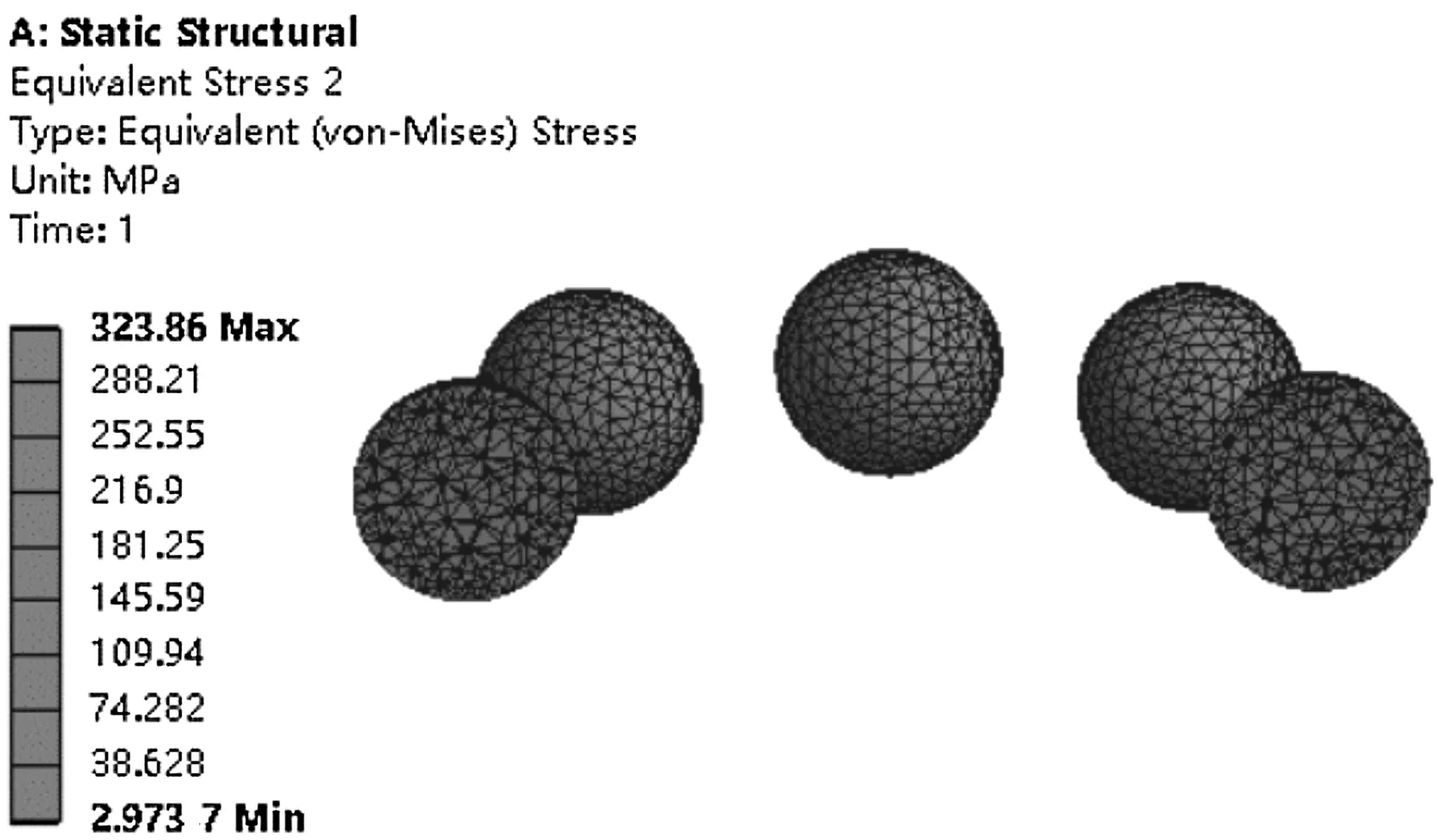
(b)第一级轴承单元滚动体等效应力云图

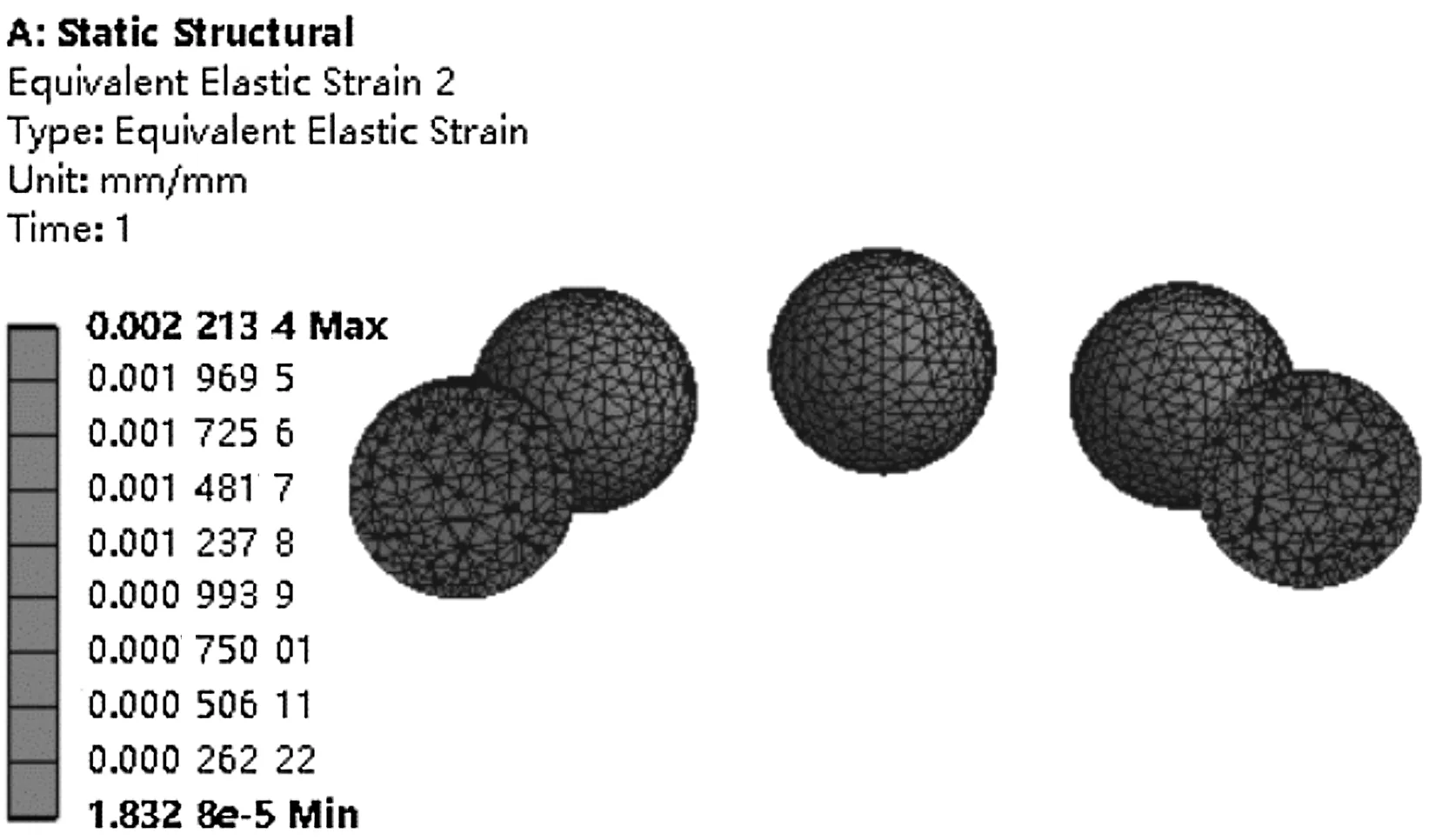
(c)第一级轴承单元滚动体等效应变云图

由图5可知:(1)轴承组等效应力最大值为1 019.3 MPa,主要集中在第一级碟簧对间的接触区域,这是因为碟簧对间接触面积小而产生的应力集中现象;(2)第一级轴承单元等效应力最大值323.86 MPa,同理第二级轴承单元等效应力最大值为329.6 MPa,均集中在滚动体与滚道面接触区域;(3)第一级轴承单元等效应变最大值为0.002 213 4,同理第二级轴承单元等效应变最大值为0.002 424 2,均集中在滚动体与滚道面接触区域。

3.2.2 三级轴承组仿真及结果分析

三级、四级、五级轴承组的具体仿真分析过程均与上述二级轴承组的分析过程相同,因此,此处笔者不再赘述。

三级轴承组的仿真分析结果如图6所示。

(a)三级轴承组等效应力云图

(b)第一级轴承单元滚动体等效应力云图

(c)第一级轴承单元滚动体等效应变云图

由图6可知:(1)三级轴承组最大等效应力为708.26 MPa,主要集中在第一级碟簧对间的接触区域;(2)第一级轴承单元等效应力最大值为232.27 MPa,同理第二、三级轴承单元等效应力最大值分别为225.85 MPa、223.14 MPa,均集中在滚动体与滚道面接触区域;(3)第一级轴承单元最大等效应变为0.001 735 6,同理第二、三级轴承单元最大等效应变分别为0.001 689 7、0.001 681 5,均集中在滚动体与滚道面接触区域。

3.2.3 四级轴承组仿真及结果分析

四级轴承组的仿真分析结果如图7所示。

(a)四级轴承组等效应力云图体等效应力云图

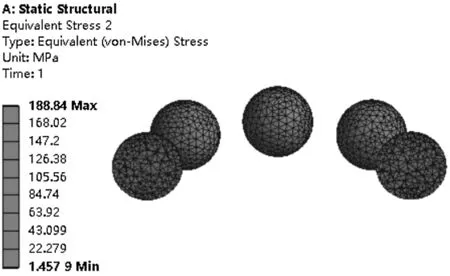
(b)第一级轴承单元滚动体等效应力云图

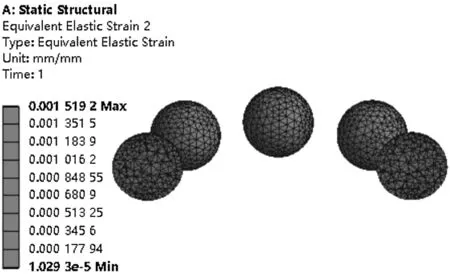
(c)第一级轴承单元滚动体等效应变云图

由图7可知:(1)四级轴承组最大等效应力为566.18 MPa,主要集中在第一级碟簧对间的接触区域;(2)第一级轴承单元等效应力最大值为188.84 MPa,集中在滚动体与滚道面接触区域;同理,第二、三、四级轴承单元等效应力最大值分别为181.41 MPa、183 MPa、172.72 MPa;(3)第一级轴承单元最大等效应变为0.001 519 2,集中在滚动体与滚道面接触区域;同理,第二、三、四级轴承单元最大等效应变分别为0.001 457 1、0.001 396 5、0.001 339。

3.2.4 五级轴承组仿真及结果分析

五级轴承组的仿真分析结果如图8所示。

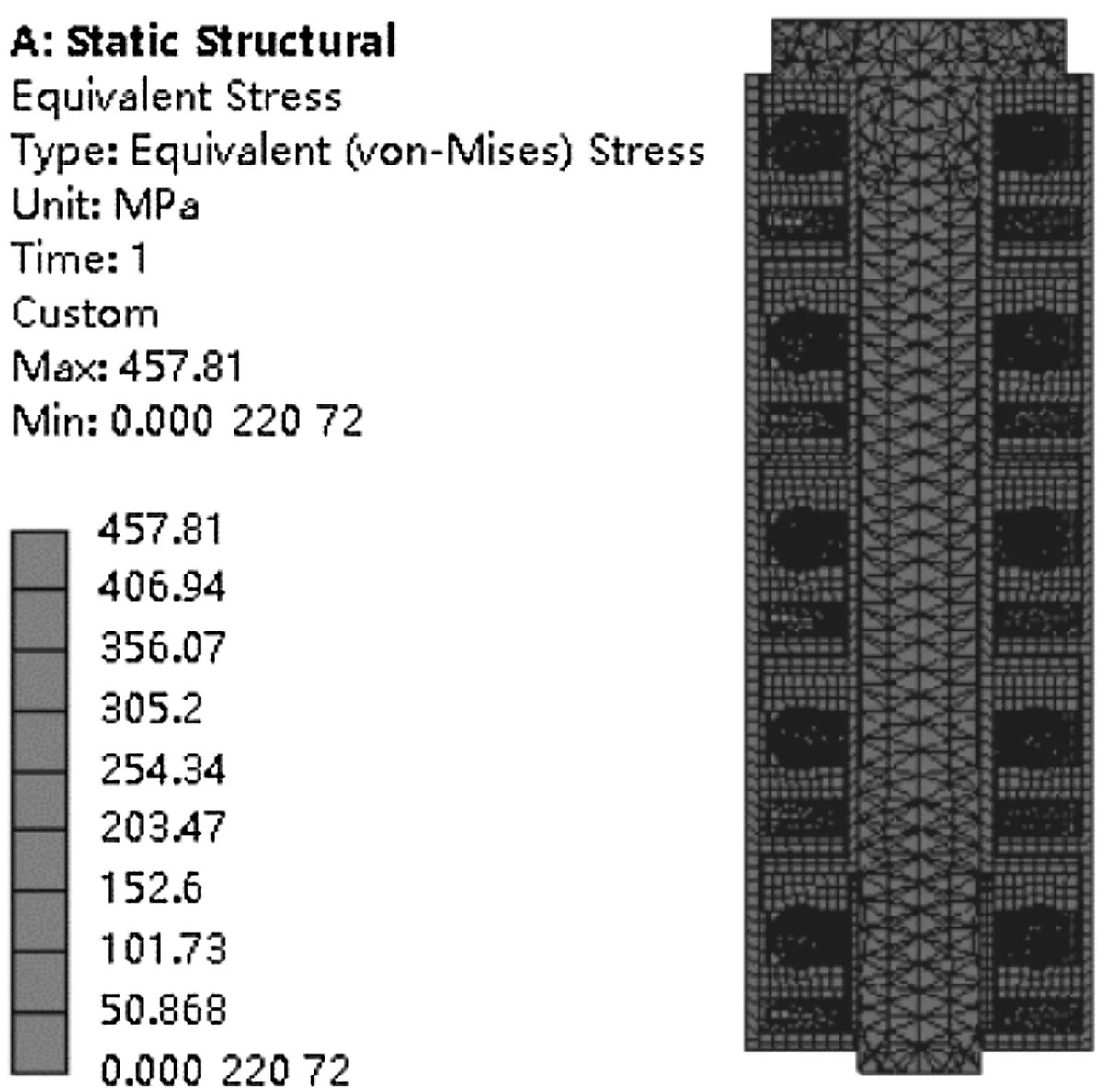
(a)五级轴承组等效应力云图

(b)第一级轴承单元滚动体等效应力云图

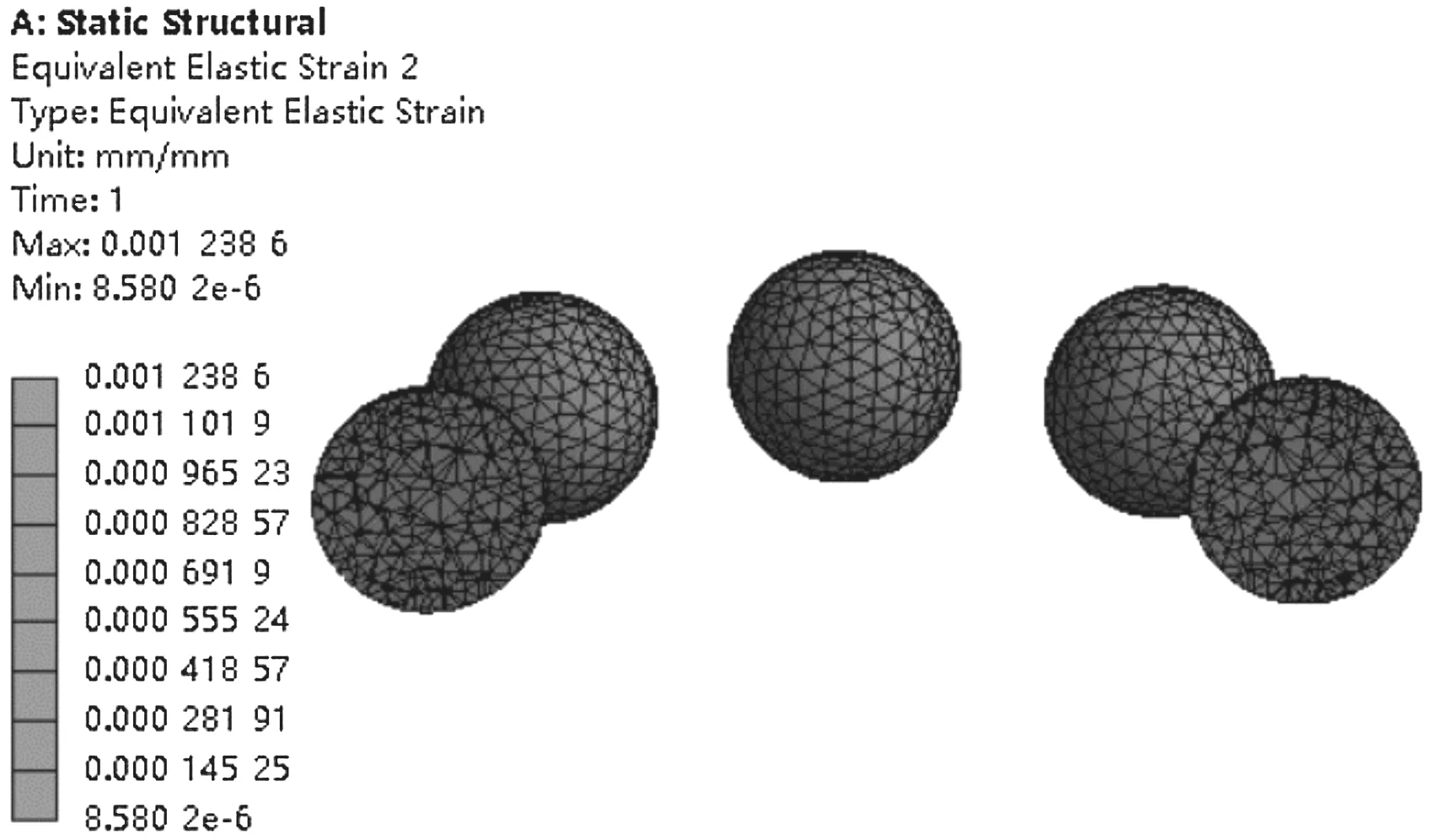
(c)第一级轴承单元滚动体等效应变云图

由图8可知:(1)五级轴承组最大等效应力值为457.81 MPa,主要集中在第一级碟簧对间的接触区域;(2)第一级轴承单元最大等效应力为168.22 MPa;同理,第二、三、四、五级轴承单元最大等效应力分别为159.61 MPa、154.78 MPa、153.22 MPa、141.55 MPa,均集中在滚动体与滚道面接触区域;(3)第一级轴承单元最大等效应变为0.001 238 6;同理,第二、三、四、五级轴承单元最大等效应变分别为0.001 169、0.001 174 9、0.001 138 2、0.001 030 4,均集中在滚动体与滚道面接触区域。

4 轴承组均载效果及总体承载能力

综合上述仿真数据可知,随着轴承组级数的增加,轴承组最大等效应力、轴承单元等效应力、应变均呈递减趋势,各级碟形弹簧变形均匀。因此,笔者主要以等效应力为依据来表征轴承组的均载效果及承载能力。

4.1 轴承组均载效果

为了便于对比分析,笔者将多级轴承组轴承单元等效应力仿真数据制作成表,如表3所示。

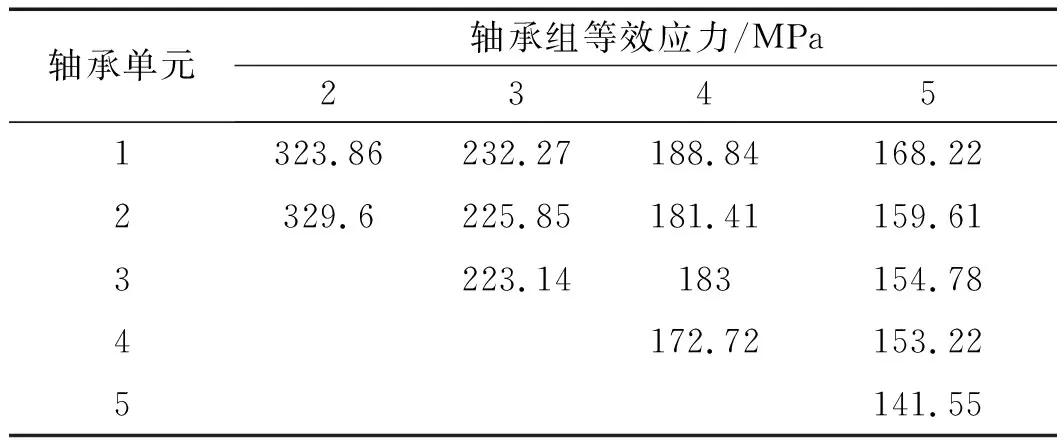
表3 多级轴承组轴承单元等效应力

为了更好地表征轴承组的均载性能,笔者引入量化评价参数—均载率[20]。均载率是用于表征轴向载荷在各级轴承单元间分配均匀程度的指标,其定义为:

(8)

(9)

式中:η—均载率,%;δmax,δmin—施加在轴承单元上的最大等效应力、最小等效应力,MPa;δm—算数平均等效应力,MPa;δa—轴承组各级轴承单元总等效应力,MPa;Z—轴承组级数。

笔者利用公式(8,9)计算所得的均载率数值制作成表,并绘制成点线图,如图9所示。

图9 轴承组均载率

从图9可见:轴承组均载率达到82%以上,均载效果良好,有效避免了个别轴承单元过载现象的发生,充分提高了轴承单元的承载能力及效率。

但随着轴承组级数的增加,轴承组均载效果逐渐降低,这是由于选取的碟形弹簧是在标准的基础上设计的非标支撑,从而导致配套的内套筒轴向尺寸精度过高,而软件自身的精度有限,致使轴承组在装配时元件间不可避免地存在微量轴向间隙,如图10所示(仅为其中一种可能性)。

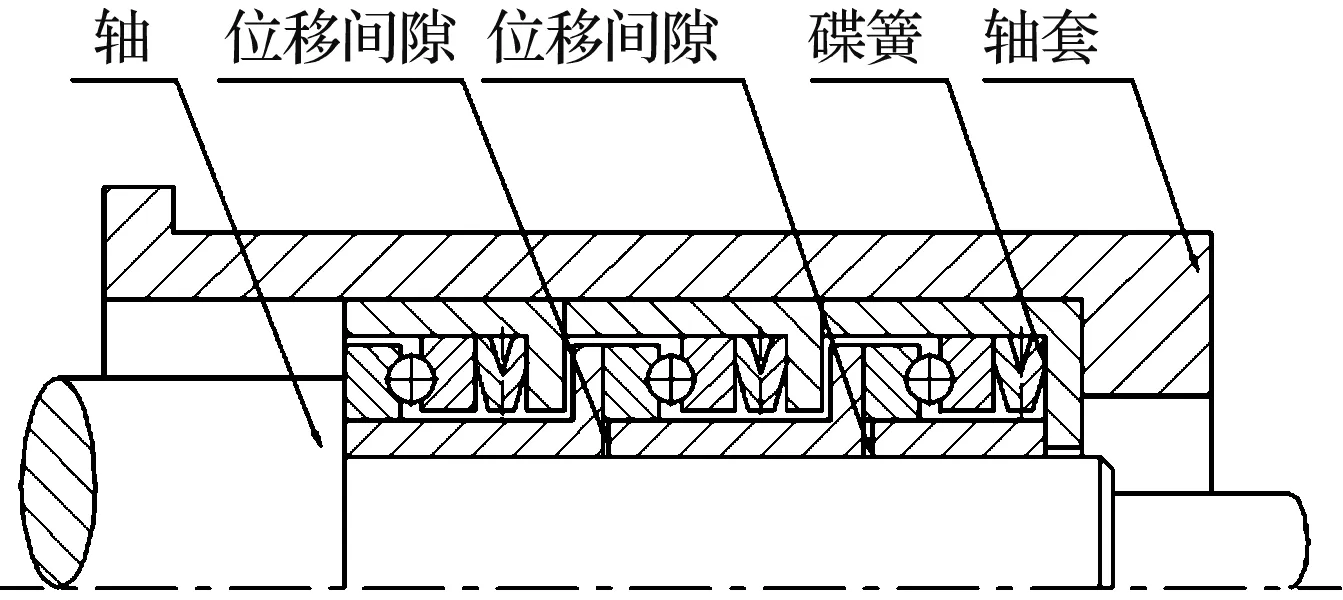
图10 元件间的轴向间隙

由图10可见:元件间存在的微量轴向间隙使得各级碟形弹簧无法同时承载,必然导致各级轴承单元受力不均,即便碟形弹簧的轴向刚度满足均载的配比要求,实际传力也会发生变化;此外,若碟簧外圆面与外套筒内圆面存在较大摩擦力,也会改变系统的力平衡关系,导致轴承组的均载效果随着轴承组级数的增加而进一步降低。

4.2 轴承组总体承载能力

为了便于对比分析,笔者将轴承组最大等效应力值数据制作成表,并绘制成点线图,如图11所示。

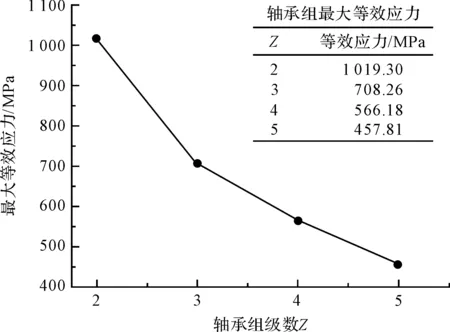
图11 轴承组最大等效应力

由图11可见:随着轴承组级数的增加,轴承组最大等效应力呈递减趋势;可见轴承组由于碟簧对间应力集中随轴承组级数的增加而减弱,直至忽略不计。

为便于对比分析,笔者将多级轴承组轴承单元最大等效应力值制作成表,并绘制成点线图,如图12所示。

从图12中可预测的是,在轴向尺寸允许的情况下,理论上轴承单元最大等效应力值会随着轴承组级数的增加,一直呈递减趋势。

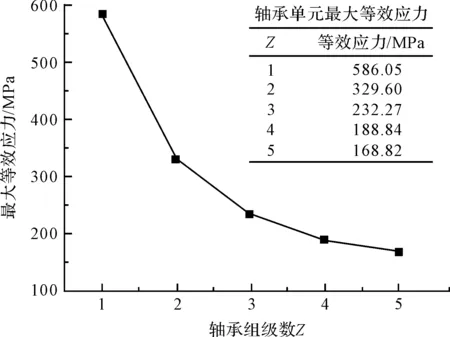
图12 轴承单元最大等效应力

在轴向载荷一定的情况下,笔者将多级轴承组对原结构等效应力的减少比例,及与上一级减少比例制作成表,如表4所示。

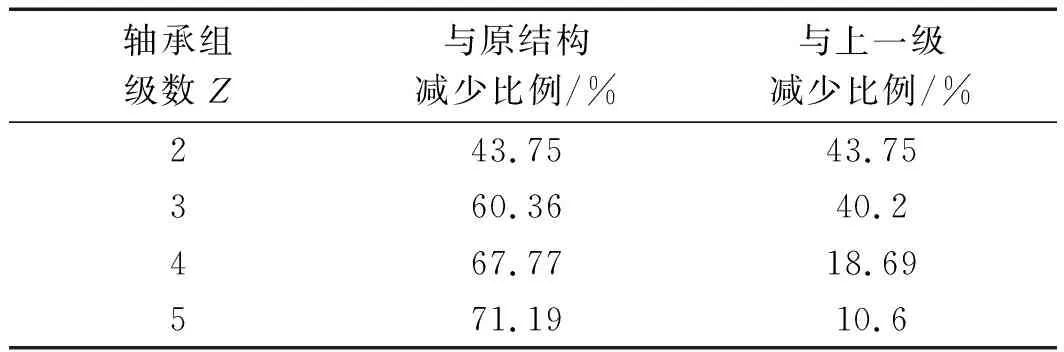
表4 轴承组等效应力减小比例

从表4中可见:二级、三级、四级、五级轴承组对原结构等效应力的减少比例分别为40.75%、60.36%、67.77%、71.19%;同时,三级轴承组等效应力较二级轴承组减少了40.2%,四级轴承组等效应力较三级轴承组减少了18.69%,五级轴承组等效应力较四级轴承组减少了10.6%。由此可见,轴承组可以有效地提高了轴承的承载能力。

笔者将多级轴承组的等效应力减小比例数据绘制成图,如图13所示。

图13 多级轴承组等效应力减小比例

从图13可见:轴承组的优化效果与轴承组级数是成正比的,但轴承组的优化程度随轴承组级数的增加而降低,即轴承组级数超出一定范围,其优化效果可忽略不计。

因此,在轴承组投入使用前,需根据实际工况选取合适的轴承组级数,以追求效益的最大化。

5 结束语

为解决限径轴承轴向力过大导致系统整体寿命受限这一关键技术难题,笔者设计了串行轴承组结构,旨在使轴承组轴承单元平均承担轴向载荷以求提高系统整体寿命;应用数值仿真方法对比分析了轴承组与原结构的应力、应变特征。

研究结论如下:

(1)串行轴承组实现了对轴向载荷的均载效应,突破了径向尺寸的限制,成功解决了限径轴承因轴向载荷过大导致寿命过短的问题;

(2)轴承组均载率在82%以上,均载效果良好,各级轴承单元碟簧变形量小且均匀,有效提高了轴承组件的承载能力;

(3)轴承组额定动载荷大,轴承组级数对原结构的优化效果是成正比的,即在轴向载荷一定的情况下,二级、三级、四级、五级轴承组对原结构等效应力的减少比例分别为40.75%、60.36%、67.77%、71.19%,有效减少了轴承单元的轴向载荷。

因为串行轴承组的承载能力及均载性能仍有待提高,所以在下一步的研究中,笔者将着手对轴承组的各组成元件进行优化设计,以求提高轴承组的承载能力及均载性能,同时进行必要的实验分析。