基于时延约束势随机共振的机械故障诊断方法研究*

李志星,王光进,鲍慧茹

(1.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室,北京 102612;2.内蒙古科技大学 机械工程学院,内蒙古 包头 014010;3.包头职业技术学院,内蒙古 包头 014030)

0 引 言

随着科学技术的发展和工业应用的迫切需要,信号检测已经成为提取机械设备微弱故障信号的重要方式[1,2]。目前,最常用的信号检测方法有奇异值分解[3]、小波变换[4，5]、整体经验模态分解[6]等。这些方法主要通过对噪声进行抑制或去除的方式,来实现对故障信号的检测。但是在去除噪声的同时,也导致了有用信号的损失,从而降低了检测精度。因此,传统的信号检测方法已经不能满足从强噪声环境中提取机械设备微弱故障信号的需要。

为了消除传统方法的这种不利影响,随机共振采用将噪声能量转换成信号能量的方法,提高了输出信噪比,进而有利于微弱信号的提取。意大利BENZI R等学者[7]于1981年首次发现并提出了随机共振现象,以解释冰期周期性递归的问题。

最初,随机共振满足绝热近似理论,并受到小参数条件的限制[8]。但是在实际的工程应用中,大多数信号都是大参数信号,这导致随机共振无法满足绝热近似理论。为了突破这一局限性,LENG Yong-gang等人[9]提出了一种二次采样的随机共振方法,实现了大参数信号向小参数信号的转变,从而满足了绝热近似理论的条件。LIN Min等人[10]研究了一种调制随机共振方法,将高频载波调制成低频信号,实现了大参数条件下,从强噪声中提取微弱故障信号的目的。

为了获得更好的信号检测效果,许多学者提出了一些新的方法来对随机共振进行更深入的研究。LEI Ya-guo等人[11]提出了一种自适应随机共振方法,利用蚁群算法的优化能力,实现了对行星齿轮箱的故障诊断。HE Qing-bo等人[12]提出了新的多尺度噪声调整方法,提高了旋转机械故障的识别能力,并用实际的振动信号对此进行了验证。时培明等人[13]利用非线性耦合双稳态随机共振增强了故障特征信号,对实际的轴承故障进行了诊断。李志星[14]研究了势模型对随机共振的影响,分析了新势模型的优越性,提高了新方法在微弱故障特征提取时的输出能力。

值得注意的是,上述研究都是以经典双稳态随机共振模型为基础的方法。经典随机共振是一个短记忆系统,时延和反馈因素常常被忽略。然而,时延和反馈因素对系统输出信噪比有很大影响。目前,已有学者对时延反馈理论做了一些研究,他们发现时延反馈随机共振可以提高微弱信号的检测效果。LU Si-liang等人[15]提出了一种时延反馈随机共振的信号提取方法,并将其用于旋转机械的故障诊断。ZHOU Bing-chang等人[16]研究了一种三分频噪声驱动的时滞双稳态系统中的随机共振现象。SHAO Rui-hua等人[17]研究了弱周期信号驱动的时滞双稳态系统的随机共振性能。韩松久[18]则进一步研究了时延三稳态和周期势随机共振,并在轴承故障诊断中取得了较好的效果。

因此,有必要对随机共振势模型进行优化,进一步研究时延和反馈因素对输出信噪比的影响[19]。为此,本文提出一种时延约束势双稳态随机共振方法,并通过理论分析、仿真和实验的方法进行研究。

1 时延约束势随机共振方法

1.1 时延约束势随机共振势模型

为了增强经典双稳态随机共振的系统性能,本文提出了一种时延约束势的双稳态势模型,其势函数方程如下所示:

(1)

式中:g,n—系统参数,且两者都为正实数。

时延约束势双稳态随机共振的势函数,如图1所示。

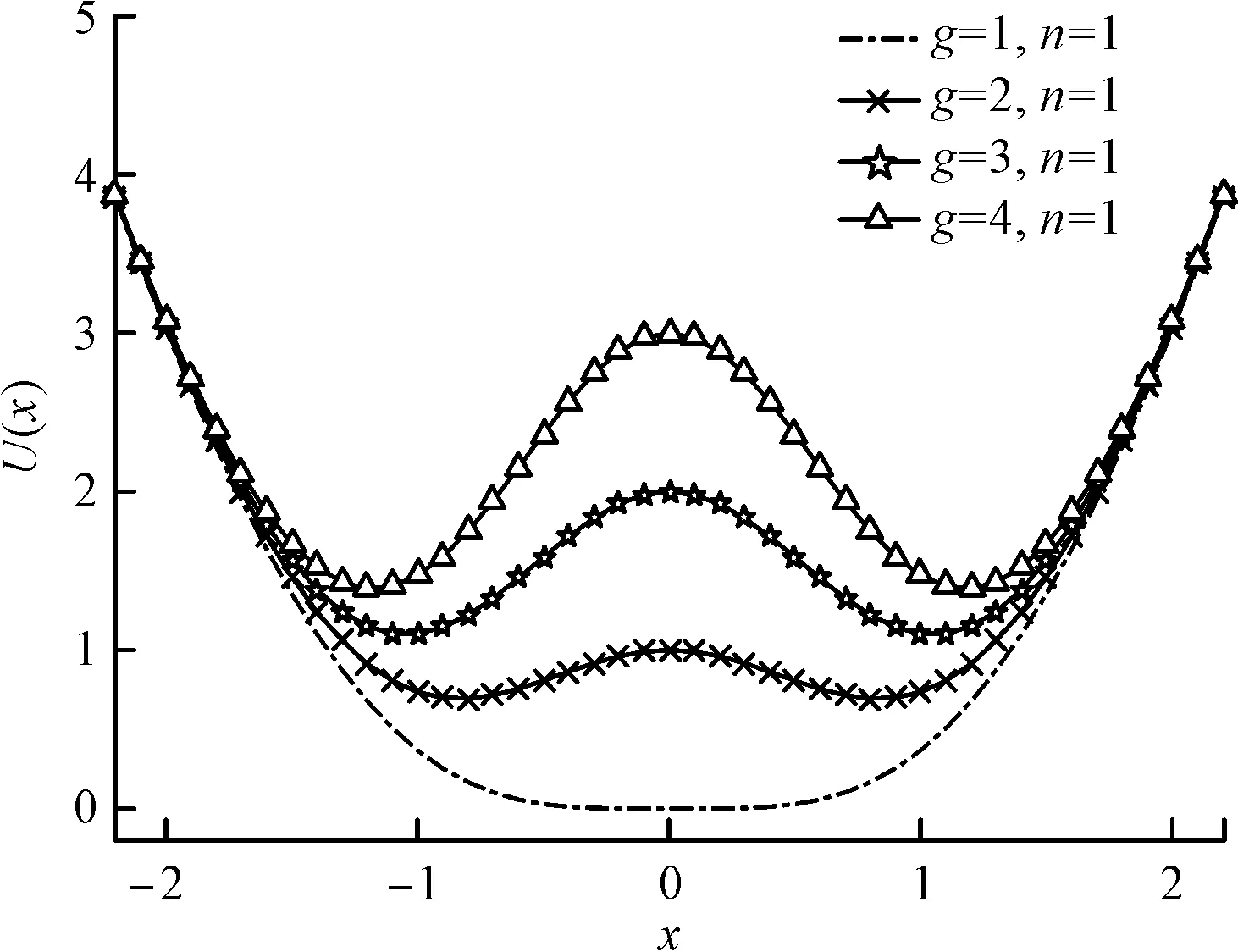
(a)固定n的值,单独调节g的值

(b)g值不变时,调节n的值

由图1(a)可知:固定n的值,单独调节g的值可以改变势垒的高度,随着g的增大势垒高度逐渐变大;

在图1(b)中,当g值不变时,调节n的值可以改变势阱宽度和势垒高度，即随着n的增大,势阱宽度和势垒高度也逐渐增大(然而对于经典双稳态势函数,其势结构是由参数a、b共同确定,无法通过调节参数来改变某个势特征的同时,保持其他特征不变)。

综上分析可知:时延约束势双稳态势函数可以通过参数的变化,实现势垒高度和势阱宽度的独立调节,使粒子由单稳态势阱运动变为双稳态势阱间运动,完成单势阱和双势阱之间的转换,具有更好的输出效果。

为了不失一般性,本文取a=1,b=1,φ=0来进行简化计算。

在经典随机共振公式中加入时延和反馈因子,则方程写为[20]:

(2)

式中:β—反馈强度;τ—时延长度。

本文引入时延约束势双稳态随机共振系统,将式(1)代入式(2),可得:

(3)

式(3)是一个非马尔科夫过程,利用概率密度法可化为马尔科夫过程。

近似时延Fokker-Planck方程如下[21]:

(4)

式中:hθ—条件平均漂移。

hθ可表示为:

(5)

其中:xτ=x(t-τ)。

则有:

(6)

进而可得:

(7)

另外,P(xτ,t-τ|x,t)代表零阶近似马尔科夫链转移概率密度,其方程满足[22]:

(8)

将式(8)代入式(5),通过推导可得出:

(9)

进一步可推导出等效朗之万方程的表达式:

(10)

由式(10)和式(3)比较可知,时延反馈随机共振系统中出现了一耦合项。

在不考虑周期信号的情况下,式(10)的等效时延势函数可导出为[23]:

(11)

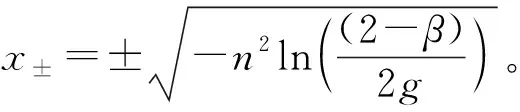
然后,式(10)的粒子在两个势阱之间的跃迁率可推导为[24]:

(12)

式中:γ+,γ-—粒子从左边到右边势阱的跃迁率,反之亦然。

在小参数限制的条件下,方程(12)可近似为:

(13)

接下来,系统的输出功率谱密度函数可以表示为[25]:

(14)

式中:S1(ω),S2(ω)—信号和噪声的输出功率谱。

N和M的表达式书写如下:

(15)

(16)

因为A≪1,频率Ω,S(ω)只能取正值,式(14)变为:

(17)

(18)

随即,系统的输出信噪比可以表达为:

(19)

把式(17,18)代入式(19),输出信噪比最终可以写为:

(20)

由式(20)可知,信噪比的大小受到不同参数的影响。

输出SNR与噪声强度D的关系曲线,如图2所示。

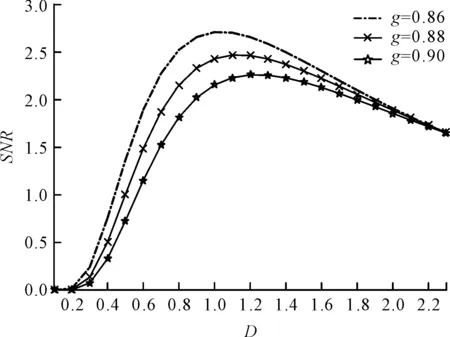
(a)当n=3.55,β=1,τ=0.85,A=1.5时,信噪比随g的变化

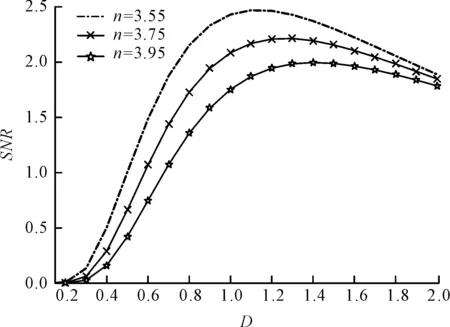
(b)当g=0.88,β=1,τ=0.85,A=1.5时,信噪比随n的变化

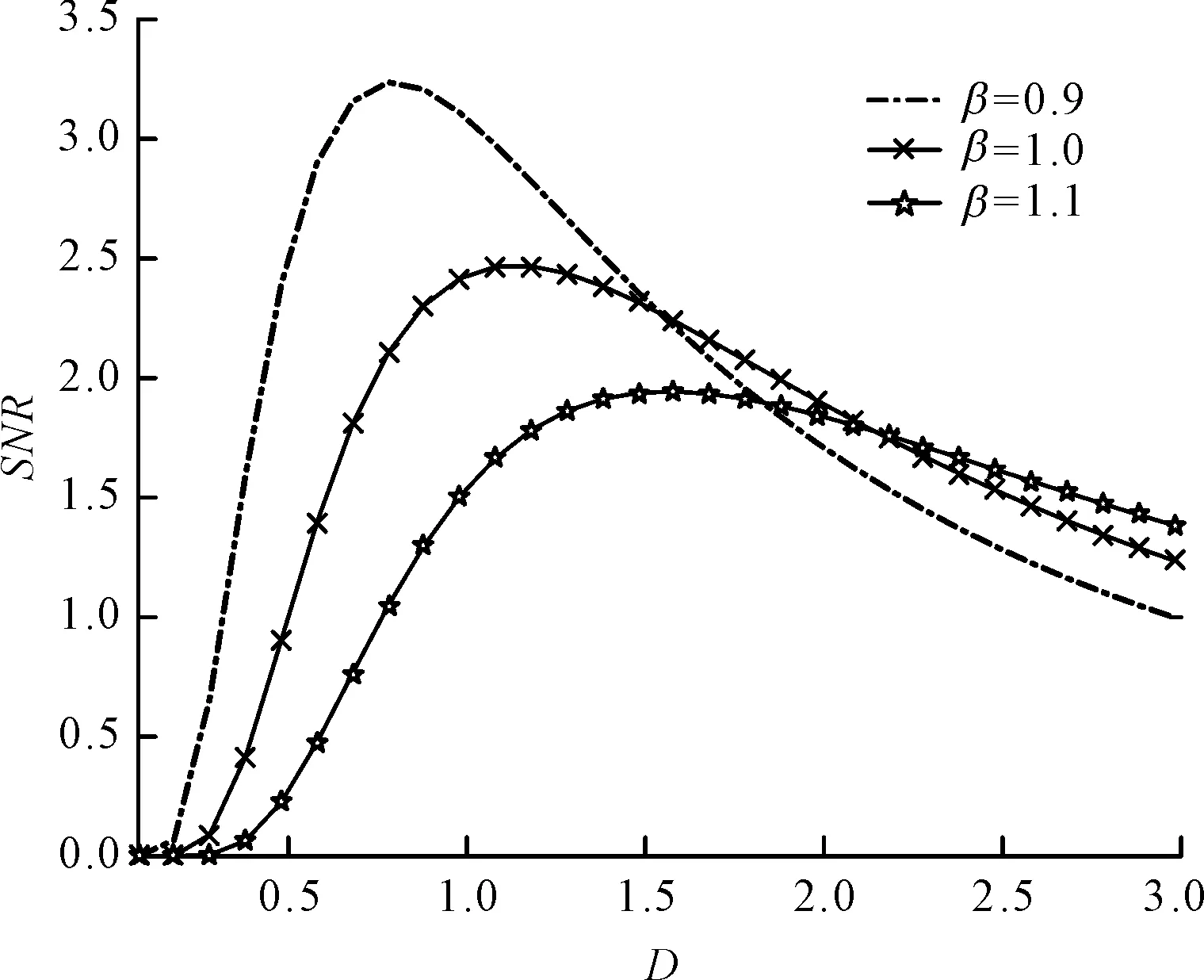
(c)当g=0.88,n=3.55,τ=0.85,A=1.5时,信噪比随β的变化

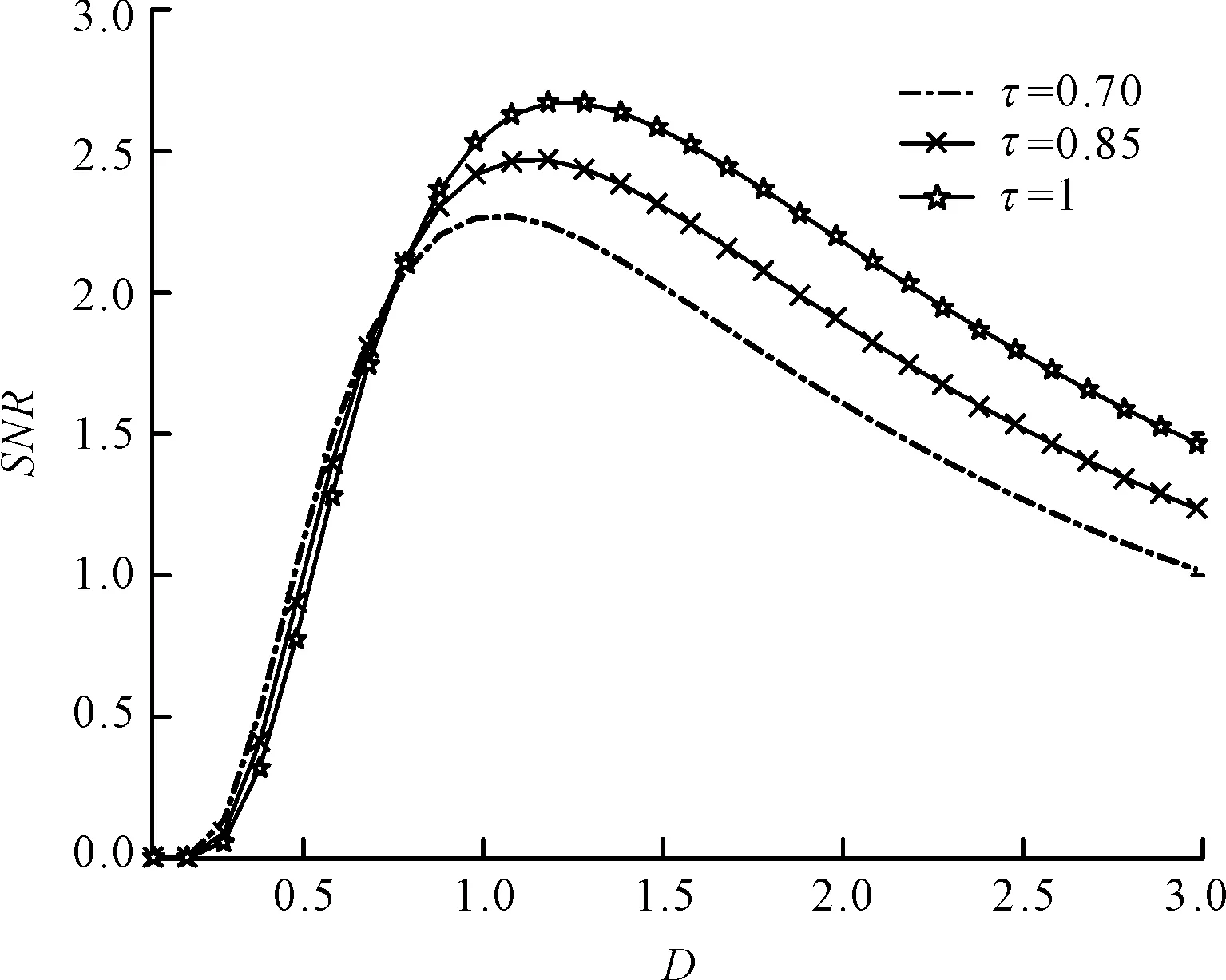
(d)当g=0.88,n=3.55,β=1,A=1.5时,信噪比随τ的变化

其曲线变化趋势为:SNR随着噪声的增加而增大,达到最大值后再减小,符合随机共振规律。

从图2(a,b)可知,输出SNR的峰值随着参数g和参数n的增大而减小,并且向右移动;

从图2(c)可知,随着反馈强度β的增加,输出信噪比变小,粒子从一个势阱跃迁到另一势阱所需要的能量增加,使得SR的效果不明显;

从图2(d)可知,随着时延长度τ的增加,输出信噪比变大,粒子很容易通过势垒的阻挡,实现势阱之间的跃迁,并且SR的效果明显。

1.2 时延约束势随机共振的微弱信号检测方法

在实际应用中,噪声力和周期力通常是固定的,因此,随机共振的信号检测效果主要受到势阱力的作用,而势阱力大小主要体现在势参数的变化。通过上节内容可知,信噪比输出与噪声强度的关系受到不同参数的影响,当时延参数、反馈参数、势参数合理匹配时,其共振效果将达到最佳。

为了处理不符合小参数条件的工程信号,需要改进系统模型,并用四阶龙格-库塔方程得到输出。

本文采用输出SNR作为评价时延约束势随机共振的性能指标。该SNR公式定义如下:

(21)

较大SNR值能更好地区分周期信号和噪声。

时延约束势随机共振的微弱信号检测方法如图3所示。

图3 时延约束势随机共振的微弱信号检测方法

该流程描述如下:

(1)数据处理。利用希尔伯特变换解调原始信号得到包络信号,随后对包络信号进行移频变尺度处理以符合小参数条件;

(2)初始化与优化参数。利用蚁群算法初始化和优化反馈参数β,时延参数τ和势参数g、n的计算范围;

(3)计算信噪比。通过龙格库塔方程计算得出输出信号波形,然后通过式(21)计算信噪比;

(4)输出确定。得到最大输出信噪比以及相应的最优参数组合;

(5)信号识别。将最优参数组合输入到时延约束势随机共振系统,最终得出时延约束势随机共振的时域波形和频谱,从而实现对故障特征信号的识别。

2 仿真验证

为了验证时延约束势随机共振方法的有效性,本文将具有高斯白噪声的周期性脉冲信号作为仿真滚动轴承的故障信号,并用所提方法进行了处理。

仿真故障信号由以下公式产生:

(22)

式中:A—信号幅值;f—载波频率;d—衰减率;n(t)=[t/Td]—用于控制脉冲周期出现;Td—脉冲间隔;fd—特征频率;D—噪声强度;η(t)—零均值和单位方差的高斯白噪声;采样时间为1 s。

仿真结果如图4所示。

图4 仿真信号

图4(a,b)分别为没有加入噪声和加入噪声的轴承故障信号。同时,加噪仿真信号的频谱和包络频谱如图4(c,d)所示。由于背景噪声太强导致特征频率60 Hz被淹没,无法准确获得轴承的故障特征频率。

本文采用时延约束势随机共振方法处理加入噪声的仿真信号,所得的时域和频谱图如图5所示。

图5 时延约束势随机共振方法

在图5(b)中:故障特征频率能够清晰地看到,其所对应的频谱峰值为0.169 9,周围第二高点的值为0.046 86,两者相差0.123 04。

为了更好地比较两种方法的提取效果,本文用经典双稳态随机共振方法处理滚动轴承的故障信号。该方法的时域和频谱图如图6所示。

图6 经典双稳态随机共振方法

在图6(b)中可知:特征频率处的频谱峰值为0.078 41,第二高点的值为0.037 46,两峰值的差为0.040 95。

综上所述:经典双稳态随机共振方法在故障特征频率处的频谱峰值低于所提出的方法,并且特征频率周围噪声干扰较大、差值较小。因此,所提出的方法对微弱故障特征的提取效果更好。

3 实验验证

为了进一步验证仿真实验的结果,笔者将所提出的方法和经典双稳态随机共振方法一起应用于轴承外圈的故障特征提取实验。

实验中采用的机械设备(轴承外圈)故障综合实验台如图7所示。

图7 机械设备故障综合实验台

实验所选用的滚动轴承型号为ER-16K,其主要几何参数如表1所示。

表1 滚动轴承的主要几何参数

采样频率为2 560 Hz,轴承转速为2 400 r/min,轴承各部件的故障特征频率如表2所示。

表2 滚动轴承的故障特征频率

其中,fr=40 Hz,计算得到轴承外圈的故障特征频率为143.08 Hz。

原始振动信号的时域、频谱和包络谱图如图8所示。

图8 原始振动信号

从图8中可以看出:由于特征信号受到强噪声的干扰,无法在频谱和包络频谱中识别出轴承外圈故障的特征频率。

对于图8中无法识别故障特征的情况,笔者应用所提出的方法,来提取轴承的故障特征频率,其输出的时域与频谱图如图9所示。

图9 时延约束势随机共振方法

从图9中的频谱可知:轴承外圈的故障特征频率为142.7 Hz,与理论值143.08 Hz很相近,频谱峰值与周围噪声最高点之差为0.086 03,据此可以得出轴承的外圈上发生了故障。由此可见,该方法能够提取出轴承的故障特征。

为了验证该方法的优越性,笔者应用经典双稳态随机共振方法,来提取轴承的故障特征频率,其输出的时域与频谱图如图10所示。

图10 经典双稳态随机共振方法

在图10(b)中,相同的故障特征频率也被经典随机共振方法提取,但是其频谱峰值只高出最大噪声0.009 76。

在轴承外圈的故障特征提取实验中,采用以上两种方法,在故障特征频率处得到的频谱峰值分别为0.154和0.031 39。

通过以上两种方法的对比可知,在机械设备故障的特征提取方面,所提出的方法比经典双稳态随机共振方法具有更高的谱峰值、更好的识别效果。

4 结束语

在实际工作环境中,机械设备的故障特征很难被提取出来,因此笔者提出了一种基于时延约束势随机共振的机械故障信号检测方法。首先，建立了时延约束势随机共振模型,研究了系统参数、时延长度和反馈强度对信噪比和噪声强度关系的影响;然后，利用蚁群算法的参数优化能力,实现了随机共振系统的最佳匹配;最后,将提出的方法应用于仿真故障信号和实际轴承外圈故障信号的实验中。

理论分析、仿真和实验验证所得结论如下:

(1)通过对系统参数的调节可以得到多种势模型结构,实现了对系统随机振动的控制,比传统双稳态势模型效果更好;

(2)在约束势随机共振系统的基础上引入了反馈强度和时延长度,并且理论推导了输出信噪比,分析得出了各个参数对信噪比的影响;

(3)自适应蚁群算法以信噪比作为评价指标,通过优化系统参数、反馈强度和时延长度,可以实现更好的输出性能;

(4)与经典双稳态随机共振方法相比,所提出的方法不仅可以有效地提取故障特征,而且其噪声分量较小,具有更好的微弱信号检测效果。

综上可知,该方法在机械故障诊断的信号提取方面取得了一定的进展。后续的工作中,笔者将在势模型的选取以及参数的优化匹配上继续作进一步的研究。